合成法和正交分解法-课件

正交分解法与合成法湖南省祁阳县第四中学黄冬成一、知识讲解1、正交分解法：将力分解到运动方向和垂直运动方向例1、如图所示，质量为4 kg 的物体静止于水平面上，物体与水平面间的动摩擦因数为0.5，物体受到大小为20Ｎ，与水平方向成30°角斜向上的拉力F 作用时沿水平面做匀加速运动，求物体的加速度是多大?（g 取10 m/s 2）解析：以物体为研究对象，其受力情况如图所示，建立平面直角坐标系把F 沿两坐标轴方向分解，则两坐标轴上的合力分别为,sin cos G F F F F F F N y x -+=-=θθμ物体沿水平方向加速运动，设加速度为a ，则x 轴方向上的加速度a x ＝a ，y 轴方向上物体没有运动，故a y ＝０，由牛顿第二定律得0,====yy xx maF ma maF所以0sin ,cos =-+=-G F F ma F F N θθμ 又有滑动摩擦力N F F μμ=以上三式代入数据可解得物体的加速度a =0.58 m/s 2 说明：当物体的受力情况较复杂时，根据物体所受力的具体情况和运动情况建立合适的直角坐标系，利用正交分解法来解．2、合成法：将力合成到运动方向 例2、如图，沿水平方向做匀变速直线运动的车厢中，悬挂小球的悬线偏离竖直方向37°角，球和车厢相对静止，球的质量为1kg ．（g ＝10m/s 2，sin37°＝0.6，cos37°＝0.8）（1）求车厢运动的加速度并说明车厢的运动情况． （2）求悬线对球的拉力．解析：（1）球和车厢相对静止，它们的运动情况相同，由于对球的受力情况知道的较多，故应以球为研究对象．球受两个力作用：重力mg 和线的拉力F T ，由球随车一起沿水平方向做匀变速直线运动，故其加速度沿水平方向，合外力沿水平方向．做出平行四边形如图所示．球所受的合外力为F 合＝mg tan37°由牛顿第二定律F 合＝ma 可求得球的加速度为=︒==37tan g mF a 合7.5m/s 2加速度方向水平向右．车厢可能水平向右做匀加速直线运动，也可能水平向左做匀减速直线运动． （2）由图可得，线对球的拉力大小为8.010137cos ⨯=︒=mg F T N=12.5 N说明：本题解题的关键是根据小球的加速度方向，判断出物体所受合外力的方向，然后画出平行四边形，解其中的三角形就可求得结果．二、课堂检测1．如图所示，悬挂于小车里的小球偏离竖直方向θ角，则小车可能的运动情况是（ AD ） A ．向右加速运动B ．向右减速运动C ．向左加速运动D ．向左减速运动2、如图所示， m =4kg 的小球挂在小车后壁上，细线与竖直方向成37°角。

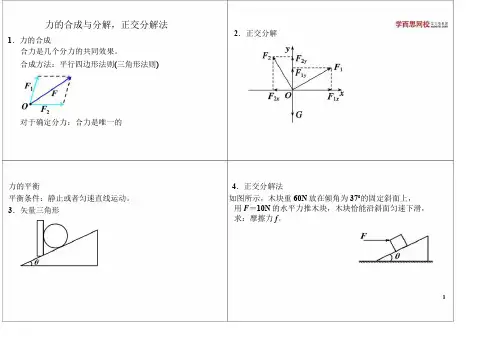
力的合成与分解，正交分解法1．力的合成合力是几个分力的共同效果。

合成方法：平行四边形法则(三角形法则)对于确定分力：合力是唯一的力的平衡 4．正交分解法平衡条件：静止或者匀速直线运动。

如图所示，木块重60N 放在倾角为37°的固定斜面上，3．矢量三角形12．正交分解用F ＝10N 的水平力推木块，木块恰能沿斜面匀速下滑，求：摩擦力f 。

【例1】如图所示。

用钢筋弯成的支架，水平虚线MN 的 【例2】如图所示，重G ＝15N 的小球，用长为l ＝1m 的上端是半圆形，MN 的下端笔直竖立。

一不可伸 细绳挂在A 点，靠在半径R ＝1.3m 的光滑大球面 长的轻绳通过动滑轮悬挂一重物G 。

现将轻绳的 上，已知A 点离球顶距离d ＝0.7m ，求小球对绳 一端固定于支架上的A 点，另一端从最高点B 处沿 的拉力和对大球的压力的大小各为多少？ 支架缓慢地向C 点靠近(C 点与A 点等高)，则绳中 拉力( )A ．先变大后不变B ．先不变后变大C ．先不变后变小D ．保持不变【例3】如图所示，绳OC 与竖直方向30°角，O 为质量不计 【例4 两小球悬挂在天花 的滑轮。

已知物B 重1000N ，物A 重400N ，物A 、B 两小球 均静止。

求： 上，使三根细线均处于直 物B 所受摩擦力为多大？ (2)OC 绳的拉力为多大？ 于静止状态。

则该力可能为图中的(A CD ．F 42，然后用力F 作用在小球A 线状态，且OB 细线恰好沿竖直方向，两小球均处 】如图所示，用两根细线把A 、B板上的同一点O ，并用第三根细线连接A 、B (1) B ．F 2【例5】如图所示，光滑圆球半径为1m，质量为6kg，静【例6】下物体A质量为m＝2kg，用两根轻绳B、C连接到止于图示位置，图中距离d为1.8m，求竖直墙壁与竖直墙上，在物体A上加一恒力F，若图中力F、台阶对球的支持力分别为多大？轻绳AB与水平线夹角均为θ＝60°，要使两绳都能绷直，求恒力F的大小。

第05讲 合成法和正交分解法整体法和隔离分析法【教学目标】1.理解共点力的平衡条件；2.掌握合成法解三力平衡、正交分解法解四个及以上力的平衡的思维方法；3.掌握隔离分析法、整体法的解题思维和方法。

【知识点击】（一）力的正交分解法1.定义：将已知力按互相垂直的两个方向进行分解的方法。

2.原则：一般选共点力的作用点为原点，在静力学中，以少分解力和容易分解力为原则（即尽量多的力在坐标轴上）；在动力学中，习惯以加速度方向和垂直加速度方向为坐标轴建立坐标系。

3.方法：物体受到多个力作用F 1、F 2、F 3…求合力F 时，可把各力沿相互垂直的x 轴、y 轴分解。

x 轴上的合力：F x =F x 1＋F x 2＋F x 3＋…y 轴上的合力：F y =F y 1＋F y 2＋F y 3＋…4.合力大小：F =F x 2＋F y 25.合力方向：与x 轴夹角设为θ，则tan θ=F y F x 。

【典例1】（多选）两个物体A 和B ，质量分别为2m 和m ，用跨过定滑轮的轻绳相连，A 静止于水平地面上，如图所示，θ=30°，不计摩擦，则以下说法正确的是 （ ）A ．绳上拉力大小为mgB ．物体A 对地面的压力大小为mg 213C．物体A对地面的摩擦力大小为mg2D．地面对物体A的摩擦力方向向右【演练1】（多选）如图所示，质量为m的木块在推力F作用下，在水平地面上做匀速运动。

已知木块与地面间的动摩擦因数为μ，那么木块受到的滑动摩擦力为（）A．μmg B．μ（mg＋Fsin θ）C．μ（mg－Fsin θ）D．Fcos θ（二）物体的受力分析1．受力分析：把研究对象在特定的物理环境中受到的所有力找出来，并画出受力图，这就是受力分析。

2．受力分析注意要点（1）防止“漏力”和“添力”，按正确顺序进行受力分析是防止“漏力”的有效措施.注意寻找施力物体，这是防止“添力”的措施之一，找不出施力物体，则这个力一定不存在。

力的合成与分解正交分解法一、力的合成1.力的合成(1)合力和力的合成：(2)共点力：特征是作用线“共点”，而不一定是力的作用点“共点”.2.平行四边形定则3.合力的大小及方向F＝F21＋F22＋2F1F2cosθ合力的方向tanβ＝F1sinθF2＋F1cosθ讨论：(1)在F1、F2大小不变的情况下，F1、F2之间的夹角θ越大，合力F越小；θ越小，合力F越大.(2)当θ＝0°时，F＝F1＋F2，为F的最大值.当θ＝90°时，F＝F21＋F22当θ＝120°且F1＝F2时，F＝F1＝F2当θ＝180°时，F＝|F1－F2|，为F的最小值(3)合力的变化范围为|F1－F2|≤F≤F1＋F2合力可以大于分力，可以等于分力，也可以小于分力.4.三角形定则：二、力的分解1.分力与力的分解一个已知力按力的效果进行分解的方法在实际问题中，一个力如何分解，应按下述步骤：(1)先根据力的实际作用效果确定两个实际分力的方向；(2)再根据两个分力的方向画出平行四边形，且注意标度选取；(3)根据平行四边形和学过的数学知识求出两个分力的大小和方向.求解方法：①平行四边形法；②正弦定理法；③相似三角形法；④余弦定理法.思维突破(1)已知力F的大小与方向以及两个分力的方向，则两个分力的大小有惟一确定解，如图2－3－7.(2)已知F的大小与方向以及一个分力的大小和方向，则另一分力的大小和方向有惟一确定解，如图(3)已知力F的大小和方向以及一个分力F1的方向和另一个分力F2的大小，如图当F2＝F sinθ时，有惟一解；当F2＜F sinθ时，无解；当F＞F2＞F sinθ时，有两解；当F2＞F时，一解.具体做法是以F的矢端为圆心，以F2的大小为半径画圆弧，与F1相切，惟一解，如图(a)；相交，两解，如图(b)；不相交，无解，如图(c)；F2＞F时，相交一点，有一解，如图(d).3.正交分解法在物理问题中，常常把一个力分解为相互垂直的两个分力，这种分解方法叫做正交分解法.求多个共点力的合力时，如果连续运用平行四边形定则求解，计算过程十分复杂，如果采用力的正交分解法求合力，计算过程就十分简单.如图2－3－5，其基本步骤是：(1)建立正交坐标系(x轴、y轴).通常选共点力的作用点为坐标原点，坐标轴的方向的选择则应根据实际问题来确定.原则是使坐标轴与尽可能多的力重合，即使需要向两坐标轴投影分解的力尽可能少，在处理静力学问题时，通常选用水平方向和竖直方向上的直角坐标，当然在其他方向较简便时，也可选用；(2)分解与坐标轴方向不重合的力；(3)沿着坐标轴方向求合力F x、F y；(4)求F x、F y的合力F，F与F x、F y的关系如下：F＝F2x＋F2y，其方向为tanα＝F y/F x注意：如果F合＝0则必然F x＝0,F y＝0,这是处理多力作用下物体的平衡问题的常用规律.例1：如图所示，F1、F2、F3恰好构成封闭的直角三角形，这三个力的合力最小的是( )例2：如图所示，质量为m的球放在倾角为α的光滑斜面上，试分析挡板AO与斜面间的倾角β多大时，AO所受的压力最小.例3：某压榨机的结构示意图如图所示，其中B 点为固定铰链，若在A 铰链处作用一垂直于壁的力F ，则由于力F 的作用，使滑块C 压紧物体D ，设C 与D 光滑接触，杆的重力不计，压榨机的尺寸如图所示，求物体D 所受压力大小是F 的多少倍？(滑块C 重力不计)例4：如图所示，在倾角为θ的粗糙斜面上，有一个质量为m 的物体被水平力F 推着静止于斜面上，已知物体与斜面间的动摩擦因数为μ，且μ＜tan θ，请你判断力F 的取值范围.作业：1.下列关于合力与分力的叙述不正确的是A .一个物体受到几个力的作用，同时也受到这几个力的合力的作用B .几个力的合力总是大于它各个分力中最小的力C .一个力分解成两个分力，可以得到无数对大小、方向不同的分力D .合力和它相应的分力对物体的作用效果相同2.运动员将杠铃举过头顶，如图所示，设两臂间的夹角为θ，以下说法中正确的是A .θ角大些，手臂承受压力也大些B .θ角大些，手臂承受压力反而小些C .θ角变化时，手臂承受压力一样D .由于条件不足，无法判断3.如图所示，A 、B 两物体的质量分别为m A 和m B ，且m A ＞m B ，整个系统处于静止状态，小滑轮的质量和一切摩擦均不计，如果绳的一端由Q 点缓慢地向左移到P 点，整个系统重新平衡后，物体A 的高度和两滑轮间绳与水平方向的夹角θ如何变化A .物体A 的高度升高，θ角变大B .物体A 的高度降低，θ角变小C .物体A 的高度升高，θ角不变D .物体A 的高度不变，θ角变小4.用三根轻绳将质量为m 的物块悬挂在空中，如图所示，已知绳AO 和BO 与竖直方向的夹角都是30°，若想保持A 、O 两点的位置不变，而将B 点下移至OB 水平，则此过程中A .OB 绳上的拉力先增大后减小 B .OB 绳上的拉力先减小后增大C .OA 绳上的拉力先增大后减小D .OA 绳上的拉力不断减小5.如图所示，AC 是上端带定滑轮的固定竖直杆，质量不计的轻杆BC 一端通过铰链固定在C 点，另一端B 悬挂一重为G 的物体，且B 端系有一根轻绳并绕过定滑轮A ，用力F 拉绳，开始时∠BCA ＞90°，现使∠BCA 缓慢变小，直到杆BC 接近竖直杆AC.此过程中，轻杆B 端所受的力A .大小不变B .逐渐增大C .逐渐减小D .先减小66.水平横梁的一端A 插在墙壁内，另一端装有一小滑轮B ，一轻绳的一端C 固定于墙壁上，另一端跨过滑轮后悬挂一质量m ＝10 kg 的重物，∠CBA ＝30°，如图甲所示，则滑轮受到绳子的作用力为(取g ＝10 m /s 2)A .50 NB .50 3 NC .100 ND .100 3 N7．2010高考如图所示，一物块置于水平地面上.当用与水平方向成600角的F 1力拉物块时，物块做匀速直线运动；当改用与水平方向成300角的F 2力推物块时，物块仍做匀速直线运动.若F 1和F 2的大小相等，则物块与地面之间的动摩擦因数为AB 、D 、8.如图所示，用两根细绳把A、B 两小球悬挂在天花板上的同一点O ，并用第三根细线连接A 、B 两小球，然后用某个力F 作用在小球A 上，使三根细线均处于直线状态，且OB 细线恰好沿竖直方向，两小球均处于静止状态，则该力可能为图中的A .F 1B .F 2C .F 3D .F 49.如图所示，用一个轻质三角支架悬挂重物， 已知AB 杆承受的最大压力为2 000 N ，AC 绳承受最大拉力为1 000 N ，∠α＝30°，为不使支架断裂，求悬挂物的重力应满足的条件？1212。

§3.3二力合成法与正交分解法高考考点：牛顿定律的应用（2）复习内容：一.二力合成法：1．如果物体在运动过程中，仅仅受到两个力的作用，采用这种方法求合力，此合力方向与物体运动的加速度方向相同。

2．合成法求加速度a:注意合力与分力的“特效性”，是一中等效替代关系，因此它们不能同时存在。

应用1-1，如图：小车的运动情况如何？加速度多大？方向怎样？o分析：如上图所示，F合不等于0，且a与F合的方向一致，在与球有共同的水平向左的加速度，合力水平向左，加速度水平向左，则有：F=mg tanαF=maa=F/m=g tanα两钟运动情况：①.向左做匀加速直线运动②.想右做匀减速直线运动课堂练习：P83第3题二. 正交分解法：若物体同时受到三个以上的共点力作用，建立平面直角坐标系，利用正交分解法：两种情况： F x 合=ma1．分解力不分解加速度，此时一般规定a 的方向为x 轴正方向：F y 合=02.分解加速度不分解力，此种方法以某力方向为x 轴正方向,把加速度分解在x 轴和y 轴上。

注：这种方法通常用于物体所受的几个力，起方向都沿正交方向，分解各个力反而不如分解加速度方便，简捷！应用2-1如图，质量为m 的人站在自动扶梯上，扶梯以加速度a 向上减速运动，a 与水平方向夹角为θ，求人受到的支持力和摩擦力。

解法一：以人为研究对象，受力分析如图建立好坐标系：根据牛顿第二定律得：x 方向：Fsin θ+fcos θ-mgsin θ=ma ① y 方向：F N cos θ+fsin θ-mgcos θ=0 ②由①②可得： F N =m(g-a sin θ)f=m a cos θf 为负，说明摩擦力的实际方向与假设方向相反，即水平向左解法二：以人为研究对象，沿水平竖直方向建立坐标系，则：a x =a cos θ,a y =a sin θf=ma x ,mg -F N =ma yF 合=m a x F 合=m a yF 合=m a求得：f=ma cosθ,F N=m(g-asinθ)课堂训练2：P82 1，2作业：课堂练习册P83 1，2，3，4，6，7，10，13。