正多边形的画法(课件精选)

常见几何图形的作图方法正多边形的画法斜度和锥度椭圆的画法圆弧连接正多边形的画法1.正六边形画法利用外接圆半径作图正多边形的画法1.正六边形画法已知外接圆直径，利用圆规、三角板作图。

正多边形的画法1.正六边形画法已知外接圆直径，利用丁字尺、三角板作图。

正多边形的画法1.正六边形画法已知外接圆直径，利用丁字尺、三角板作图。

正多边形的画法1.正六边形画法已知对边距离作图正多边形的画法1.正六边形画法已知对边距离作图正多边形的画法2.正五边形画法已知外接圆直径作图正多边形的画法2.正五边形画法已知外接圆直径作图正多边形的画法3.正n边形画法已知外接圆直径作图正七边形为例正多边形的画法3.正n边形画法已知外接圆直径作图正七边形为例斜度和锥度1.斜度斜度的画法举例画出作图基准线 作斜度1:5辅助线BA 求出AB 两点线 BA作辅助线的平行线 加深、标注尺寸斜度和锥度1.斜度斜度的画法举例画出作图基准线作斜度1:5辅助线求出AB两点线作辅助线的平行线加深、标注尺寸斜度和锥度2.锥度锥度的画法举例画出作图基准线 作锥度1:5辅助线 BA求出AB 两点线 作辅助线的平行线 加深、标注尺寸BA斜度和锥度2.锥度锥度的画法举例画出作图基准线 作锥度1:5辅助线 求出AB 两点线 作辅助线的平行线 加深、标注尺寸BA1:5椭圆的画法已知椭圆长轴AB、短轴CD。

四心圆弧法椭圆的画法已知椭圆长轴AB、短轴CD 。

四心圆弧法圆弧连接绘制机器零件轮廓时，常遇到一条线段（直线或曲线）光滑地过渡到另一条线段的情况。

如图中的R8把圆弧和直线光滑连接起来，R10把两段直线光滑的连接起来。

这种用圆弧光滑地连接相邻两线段的方法称为圆弧连接。

圆弧连接１．圆弧连接的基本作图原理圆弧与直线相切圆弧与圆弧外切圆弧与圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧连接两直线圆弧连接２．圆弧连接的基本作图方法圆弧连接两直线圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧外切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧外切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧与两圆弧内切圆弧连接２．圆弧连接的基本作图方法圆弧连接一直线一圆弧圆弧连接２．圆弧连接的基本作图方法圆弧连接一直线一圆弧小结正多边形的画法斜度和锥度椭圆的画法圆弧连接。

课题, 第4节画正多边形（课时1）学习目标, 1、知道怎样计算多边形的内角和与外角和。

2、学会计算正多边形的各个内角与外角的度数。

3、学会使用重复命令画正多边形。

教学重点, 学会使用重复命令画正多边形。

教学难点, 计算正多边形的各个内角与外角的度数教具, 计算机安装ELOGO程序（幻灯片出示学习目标多边形的相关知识）教学时间, 1课时教学过程一、谈话导入师：同学们，这节课我们学习第4节画正多边形（课时1）板书：第4节画正多边形（课时1）二、幻灯片出示学习目标学生读学习目标，明确任务。

三、多边形的相关知识（1）幻灯片出示多边形的相关知识，进行教学讲解。

（2）学生完成书上43页试试看——填空练习。

（3）教师巡视检查。

四、画正多边形1、练习做一做，书上43页编写命令，画出如图4.4所示的边长为80的正五边形。

（1）教师讲解演示。

（2）学生练习一遍。

（3）学生自主完成书上44页试试看。

（4）说一说，体验或发现。

2、练习做一做，书上44页编写命令，画出如图4.8所示的边长为60的正六边形。

六、试试看练习做一做，书上45页编写命令，画出如图4.9所示的由18个正六边形组成的图案，边长为40。

（1）试试看：学生结合书上45页图所示的提示画，自主尝试。

（2）教师巡视检查学习情况。

（3）请画成功的学生演示讲解，教师酌情补充。

（4）学生再练习一次。

七、完成巩固练习书上48页3题八、教师总结结束课课题, 第4节画正多边形（课时2）——画正五角星1、学习目标, 复习重复命令画正多边形。

2、学会使用重复命令画正五角星。

教学重点, 学会使用重复命令画正五角星。

教学难点, 对正五角星的外角的度数的理解。

教具, 计算机安装ELOGO程序教学时间, 1课时教学过程一、谈话导入师：同学们，这节课我们学习第4节画正多边形（课时1）板书：第4节画正多边形（课时2）——画正五角星二、幻灯片出示学习目标学生读学习目标，明确任务。

三、多边形的相关知识（1）幻灯片出示多边形的相关知识，进行复习。

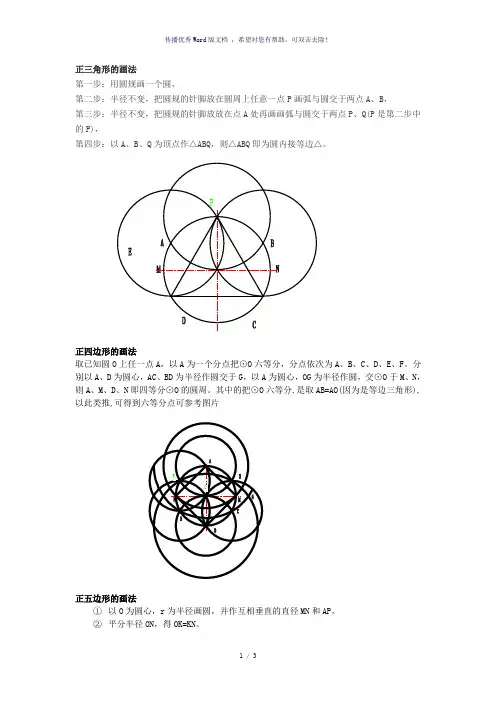
正三角形的画法第一步：用圆规画一个圆，第二步：半径不变，把圆规的针脚放在圆周上任意一点P画弧与圆交于两点A、B，第三步：半径不变，把圆规的针脚放放在点A处再画画弧与圆交于两点P、Q(P是第二步中的P)，第四步：以A、B、Q为顶点作△ABQ，则△ABQ即为圆内接等边△。

正四边形的画法取已知圆O上任一点A，以A为一个分点把⊙O六等分，分点依次为A、B、C、D、E、F。

分别以A、D为圆心，AC、BD为半径作圆交于G，以A为圆心，OG为半径作圆，交⊙O于M、N，则A、M、D、N即四等分⊙O的圆周。

其中的把⊙O六等分,是取AB=AO(因为是等边三角形),以此类推,可得到六等分点可参考图片正五边形的画法①以O为圆心，r为半径画圆，并作互相垂直的直径MN和AP。

②平分半径ON，得OK=KN。

③以K为圆心，KA为半径画弧与OM交于H，AH即为正五边形的边长。

④以AH为弦长，在圆周上截得A、B、C、D、E点，正七变形的画法PH①以定长R为半径作圆，并过圆心O作互相垂直的纵横两条直径MN、HP.②过N点任作一射线NS，用圆规取七等分，把端点T与M连结起来，然后过NT上的各点推出MT的平行线，把MN七等分.③以 M为圆心，MN为半径画弧，和PH的延长线相交于K点，从K向MN上各分点中的偶数点或奇数点（图中是 1、3、5、7各点）引射线，与交于A、B、C、M.再分别以 AB、BC、CM为边长，在圆周上从A点（或M点）开始各截一次，得到其他三点，把这些点依次连结起来，即得近似的正七边形.正八边形的画法正九边形的画法内接9边形画法：先画一个圆。

再画两个相互颠倒的内接等边三角形。

再把6角星的对角两两相连。

得到6个与两个等边三角形的底边的6个交点。

选择每一个交点为圆心，到圆内部正六边形的底边的任意一端点的距离为半径，画圆，与大圆产生2个交点。

把所有交点画出来再相连，就得到正九边形。

-----精心整理，希望对您有所帮助!。

第一步：用圆规画一个圆，第二步：半径不变，把圆规的针脚放在圆周上任意一点P画弧与圆交于两点A、B，第三步：半径不变，把圆规的针脚放放在点A处再画画弧与圆交于两点P、Q(P是第二步中的P)，第四步：以A、B、Q为顶点作△ABQ，则△ABQ即为圆内接等边△。

正四边形的画法取已知圆O上任一点A，以A为一个分点把⊙O六等分，分点依次为A、B、C、D、E、F。

分别以A、D为圆心，AC、BD为半径作圆交于G，以A为圆心，OG为半径作圆，交⊙O于M、N，则A、M、D、N即四等分⊙O的圆周。

其中的把⊙O六等分,是取AB=AO(因为是等边三角形),以此类推,可得到六等分点可参考图片①以O为圆心，r为半径画圆，并作互相垂直的直径MN和AP。

②平分半径ON，得OK=KN。

③以K为圆心，KA为半径画弧与OM交于H，AH即为正五边形的边长。

④以AH为弦长，在圆周上截得A、B、C、D、E点，正七变形的画法PH①以定长R为半径作圆，并过圆心O作互相垂直的纵横两条直径MN、HP.②过N点任作一射线NS，用圆规取七等分，把端点T与M连结起来，然后过NT上的各点推出MT 的平行线，把MN七等分.③以M为圆心，MN为半径画弧，和PH的延长线相交于K点，从K向MN上各分点中的偶数点或奇数点（图中是1、3、5、7各点）引射线，与交于A、B、C、M.再分别以AB、BC、CM为边长，在圆周上从A点（或M点）开始各截一次，得到其他三点，把这些点依次连结起来，即得近似的正七边形.正八边形的画法O正九边形的画法内接9边形画法：先画一个圆。

再画两个相互颠倒的内接等边三角形。

再把6角星的对角两两相连。

得到6个与两个等边三角形的底边的6个交点。

选择每一个交点为圆心，到圆内部正六边形的底边的任意一端点的距离为半径，画圆，与大圆产生2个交点。

把所有交点画出来再相连，就得到正九边形。