民间口诀画正五边形的画法

民间口诀画正五边形的画法
我国民间相传有正五边形的近似画法：画法口诀是：“九五顶五九，八五分两边”。

根据这个口诀，画出一个边长为2cm的正五边形。

画法：
1、用点工具作出点A。

2、选取点A，单击变换菜单下的平移命令，打开平移对话框，选择按极坐标向量平移方式（在该选项上单击鼠标，使其出现√标记）。

3、在方向输入框中输入0，在数量输入框中输入2，单击确定按钮。

得到点B（如果作图中得到的默认名称与此不同，可用文本工具为其重新命名，以下同）。

4、用线段工具连结AB，选中它，用中点命令作出它的中点G。

5、选取线段AB，用度量菜单中的长度命令得到它的长度。

6、双击长度度量值，打开计算器，输入9．5、／、10、＊，再单击AB 长度值，按下确定按钮。

得到距离1；类似地将刚才表达式中的9．5分别换成5．9和8，得到距离2和距离3。

7、选中距离1，单击变换菜单下的标记距离命令，将其作为标记距离。

8、选取中点G，单击平移命令，选择极坐标向量平移方式，在方向输入框中输入90，数量选用按标记距离，按下确定按钮。

得到点H。

9、同样地，将距离2作为标记距离，用极坐标向量方式将H点向上平移（方向90），得到点D；将距离3作为标记距离，将H点向左平移（方向180）得到点E，将H点向右平移（方向0）得到点C（平移数量均用标记距离）。

10、用线段工具连结点BC、CD、DE、EA，就得到了一个近似的正五边形。

正五边形最简单画法
正五边形是几何图形中最简单的形状，但也可以用各种方式来绘制它们，其中最简单的就是使用划线法。

划线法是一种用线条来描绘几何形状的方法，它可以帮助我们绘制精确的几何图形，而且还能控制画面中的节点和角度。

而画正五边形的最简单方法，就是使用划线法来绘制出这种形状。

首先，在一张空白的纸上绘制一个空心的圆形，以作为绘制正五边形的中心点。

然后，在周围划出五等分线，每一条等分线都指向圆心，以保证每个角度都是72°，将这五条线延伸出去，用一根细线将它们连接起来，就可以画出一个完美的正五边形了。

另外，如果画师想绘制出更加完美的正五边形，也可以使用正五边形建模法。

首先，在一张空白的纸上绘制一个空心的正五边形，在其每个顶点处用细细的线做出标记，然后以此为中心，将正五边形的边每次增加一个单位长度，每次做完，还要在其边上做出标记，这样一来，就可以绘制出更为完美的正五边形了。

此外，如果想画出更加真实的正五边形，还可以使用几何分割法。

这种方法可以用来将一个图形分割成多个等大小的几何图形，从而使图形变得更加精确和柔和。

首先，在纸上绘制出一个圆形，然后在圆形的五等分点处，划出一个半径为正五边形一半边长的小圆，将这五个小圆的圆心分别连接起来就可以画出一个完美的正五边形了。

由此可见，画正五边形有多种最简单的方法，包括使用划线法、正五边形建模法和几何分割法等。

这些方法都可以极大地提高画师画
出几何图形的准确度，使画出的图形更加完美精确。

因此，学习掌握这些画法，可以为画师创作出更加精细完美的正五边形，使其画作更具特色，令人称赞。

一边一角造五边形
介绍
五边形是一种具有五个边和五个角的多边形。

构造一个完美的
五边形可以是一个有趣的挑战，但也可能需要一些几何知识和技巧。

在本文档中，我们将探讨一种简单的方法来一边一角造五边形。

步骤
以下是一个简单的步骤来一边一角造五边形：
1. 使用尺子和直尺画一条水平线段，这将是五边形的底边。

2. 确定五边形的中心点，并在该点上画一个小圆圈。

3. 从圆圈的顶部开始，使用直尺和尺子，以逆时针方向画一条
垂直线段，该线段的长度将是五边形的高。

4. 在高的末端画一个可见的点，并标记为“A”。

5. 使用尺子，将点“A”与底边的两个端点连接，得到两条倾斜
的边。

6. 在倾斜边上，从点“A”开始，使用尺子和直尺以逆时针方向
测量和标记出五等分点，分别标记为“B”、“C”、“D”和“E”。

7. 使用尺子，分别连接点“A”和每个五等分点，得到五条边，
这将是五边形的边。

8. 检查五边形的每个角是否都接近于直角（90度），如果需要，可以进行微调。

9. 最后，擦除不必要的线条，去掉之前使用的辅助点，只保留
五边形。

结论
通过一边一角的方法，我们可以相对简单地构造一个五边形。

这种方法充分利用了几何工具的测量功能，使得五边形的构造过程
更加精确和简化。

请注意，这只是一种简单的方法，可能仅适用于小尺寸的五边形。

对于更大的五边形或需要更高精度的情况，可能需要更复杂的
技巧和工具。

希望这份文档能够帮助你了解一边一角造五边形的方法和步骤。

祝你成功！。

正五边形尺规作图的画法及其他正五边形的画法圆内接正五边形的画法如下:1、作一个圆，设它的圆心为O；2、作圆的两条互相垂直的直径AZ和XY；3、作OY的中点M；4、以点M为圆心，MA为半径作圆，交OX于点N；5、以点A为圆心，AN为半径，在圆上连续截取等弧，使弦AB=BC=CD=DE=AN，则五边形ABCDE即为正五边形。

以上两种图形的作法运用了所求图形边长与已知的线段长度的关系，用构造直角三角形的方法作出与所求图形的边长相等的线段，从而作出整个图形，这是尺规作图中常用的一种方法——等线段法，即用已知图形的线段作出与所求图形边长相等的线段。

正多边形的尺规作图是大家感兴趣的．正三边形很好做；正四边形稍难一点；正六边形也很好做；正五边形就更难一点，但人们也找到了正五边形的直规作图方法．确实，有的困难一些，有的容易一些．正七边形的尺规作图是容易一些，还是困难一些呢？人们很久很久未找到作正七边形的办法，这一事实本身就说明作正七边形不容易；一直未找到这种作法，也使人怀疑：究竟用尺规能否作出正七边形来？数学不容许有这样的判断：至今一直没有人找到正七边形的尺规作图方法来，所以断言它是不能用尺规作出的．人们迅速地解决了正三、四、五、六边形的尺规作图问题，却在正七边形面前止步了：究竟能作不能作，得不出结论来．这个悬案一直悬而未决两千余年．17世纪的费马，就是我们在前面已两次提到了的那个法国业余数学家，他研究了形如Fi （i为右下角标）＝22i（底数2指数2的i次幂）＋1 的数．费马的一个著名猜想是，当n≥3时，不定方程xn＋yn＝zn没有正整数解．现在他又猜测Fi都是素数，对于i＝0，1，2，3，4时，容易算出来相应的Fi：F0＝3，F1＝5，F2＝17，F3=257，F4=65 537验证一下，这五个数的确是素数．F5=225+1是否素数呢？仅这么一个问题就差不多一百年之后才有了一个结论，伟大的欧拉发现它竟不是素数，因而，伟大的费马这回可是猜错了！F5是两素数之积：F5＝641×6 700 417．当然，这一事例多少也说明：判断一个较大的数是否素数也决不是件简单的事，不然，何以需要等近百年？何以需要欧拉这样的人来解决问题？更奇怪的是，不仅F5不是素数，F6，F7也不是素数，F8，F9，F10，F11等还不是素数，甚至，对于F14也能判断它不是素数，但是它的任何真因数还不知道．至今，人们还只知F0，F1，F2，F3，F4这样5个数是素数．由于除此而外还未发现其他素数，于是人们产生了一个与费马的猜想大相径庭的猜想，形如22i＋1的素数只有有限个．但对此也未能加以证明．当然，形如Fi=22i+1的素数被称为费马素数．由于素数分解的艰难，不仅对形如Fi=22i+1的数的一般结论很难做出，而且具体分解某个Fi也不是一件简单的事．更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年，一位德国数学家高斯，在他仅20岁左右之时发现，当正多边形的边数是费马素数时是可以尺规作图的，他发现了更一般的结论：正n边形可尺规作图的充分且必要的条件是n=2k（2的k次幂）或2k×p1×p2×…×ps，（1，2…s为右下角标）其中，p1，p2，…，ps是费马素数．正7边形可否尺规作图呢？否！因为7是素数，但不是费马素数．倒是正17边形可尺规作图，高斯最初的一项成就就是作出了正17边形．根据高斯的理论，还有一位德国格丁根大学教授作了正257边形．就这样，一个悬而未决两千余年的古老几何问题得到了圆满的解决，而这一问题解决的过程是如此的蹊跷，它竟与一个没有猜对的猜想相关连．正17边形被用最简单的圆规和直尺作出来了，而正多边形可以换个角度被视为是对圆的等分，那么这也相当于仅用圆规和直尺对圆作了17等分，其图形更觉完美、好看．高斯本人对此也颇为欣赏，由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过)，而且在他逝后的墓碑上就镌刻着一个正17边形图案．高斯把问题是解决得如此彻底，以致有了高斯的定理，我们对于早已知道如何具体作图的正三边形、正五边形，还进而知道了它们为什么能用尺规作图，就因为3和5都是费马素数(3=F0，5＝F1)；对于很久以来未找到办法来作出的正七边形，乃至于正11边形、正 13边形，现在我们能有把握地说，它们不可能由尺规作图，因为7、11、13都不是费马素数；对于正257边形、正65 537边形，即使我们不知道具体如何作，可是理论上我们已经知道它们是可尺规作图的；此外，为什么正四边形、正六边形可尺规作图呢？因为4＝22，因为6= 2· 3而 3=F0．。

数海拾贝正五边形是一种非常重要、也非常美观的图形.它有很多特别的性质，如正五边形每个角均为108°，每条边长度相等；正五边形是旋转对称图形，但不是中心对称图形；正五边形的内角和为540°.尺规作图是指用无刻度的直尺和圆规作图，尺规作图起源于古希腊的数学课题：只使用圆规和直尺，并且只准许使用有限次，来解决不同的平面几何作图题.对于尺规构图来说，正五边形算是比较复杂的了.《几何原本》中是这样作正五边形的：先作一个等腰三角形，使其腰和底边之比为黄金比例，可以证明这个等腰三角形的顶角是36度，继而在此基础上作出正五边形（如图1）.而在《圆之吻——有趣的尺规作图》（莫海亮著）一书中，作者给出了正五边形的二十四个尺规作图方法，后面还有若干个单规、单尺作图法.虽然正五边形的作图方法多种多样，但操作起来是很复杂的，并且精确的正五边形难画.下面给出5种用尺规作出正五边形的方法.图1方法一:根据cos 72°=确定P 2点，如图2.1.作OB 的中点D (取其长度为a )；2.作圆DA (虚线所表示的圆)交直线OP 1于E 点(取其长度为(5-1)a )；3.过E 作OP 1的垂线EF ；4.以点O 为圆心，AC 为半径(4a )作圆OF 交直线EF 于点F ；5.求作OF 与圆OP 1的交点，该点即为P 2；6.依次在圆OP 1上截取P 3,P 4,P 5；7.连接P 1,P2,P 3,P 4,P 5，即可得到如图2所示的正五边形.图2方法二:根据sin 36°=长为(10-25)a 点,如图3.1.作OC 的中点D (取其长度为a )；2.作圆DP 1(虚线所表示的圆)交直线AC 于E 点(取其长度为(5-1)a )；3.选取线段EP 1的长度为(10-25)a ，即五边形的边长；4.依次在圆OP 1上截取P 2,P 3,P 4,P 5；5.连接P 1,P 2,P 3,P 4,P 5，即可得到如图3所示的正五边形.王奇62数海拾贝图3方法三:根据cos72°=确定圆心角，如图4.1.任作一条长度为4a的线段AE，并将其等分为4等份(A,B,C,D,E)；2.过点A作直线AE的垂线，并用长度AO=a确定圆心O；3.以C为圆心，CB=a为半径在CO上截取点F(取其长度为a)；4.取OF长度为(5-1)a；5.过F作OC的垂线FG；6.以点O为圆心，AE=4a为半径作圆交直线FG于点G；7.以点O为圆心，任意长度为半径作圆OP1分别交直线OC和OG于点P1和P2；8.依次在圆OP1上截取P3,P4,P5；9.连接P1,P2,P3,P4,P5，即可得到如图4所示的正五边形.图4方法四:根据cos36°确定P2点，如图5.1.作OB的中点D(取其长度为a)；2.作圆DA(虚线所表示的圆)交直线OP1于点E(取其长度为(5+1)a)；3.过E作OP1的垂线EF；4.以点B为圆心，AC为半径(4a)作圆BF交直线EF于点F；5.求作BF与圆OC的交点，该点即为P2；6.依次在圆OP1上截取P3,P4,P5；7.连接P1,P2,P3,P4,P5，即可得到如图5所示的正五边形.图563。

尺规作图的简介尺规作图是指用没有刻度的直尺和圆规作图。

一把没有刻度的直尺看似不能做什么，画一个圆又不知道它的半径，画线段又没有精确的长度。

其实尺规作图的用处很大，比如单用圆规找出一个圆的圆心，量度一个角的角度，等等。

运用尺规作图可以画出与某个角相等的角，十分方便。

尺规作图是起源于古希腊的数学课题。

只使用圆规和直尺，并且只准许使用有限次，来解决不同的平面几何作图题。

平面几何作图，限制只能用直尺、圆规。

在历史上最先明确提出尺规限制的是伊诺皮迪斯。

他发现以下作图法：在已知直线的已知点上作一角与已知角相等。

这件事的重要性并不在于这个角的实际作出，而是在尺规的限制下从理论上去解决这个问题。

在这以前，许多作图题是不限工具的。

伊诺皮迪斯以后，尺规的限制逐渐成为一种公约,最后总结在《几何原本》之中。

若干著名的尺规作图已知是不可能的，而当中很多不可能证明是利用了由19世纪出现的伽罗华理论。

尽管如此，仍有很多业余爱好者尝试这些不可能的题目，当中以化圆为方及三等分任意角最受注意。

数学家Underwood Dudley曾把一些宣告解决了这些不可能问题的错误作法结集成书。

■尺规作图的基本要求·它使用的直尺和圆规带有想像性质，跟现实中的并非完全相同：·直尺必须没有刻度，无限长，且只能使用直尺的固定一侧。

只可以用它来将两个点连在一起，不可以在上画刻度。

·圆规可以开至无限宽，但上面亦不能有刻度。

它只可以拉开成你之前构造过的长度。

■五种基本作图·作一个角等于已知角·平分已知角·作已知直线的垂直平分线·作一条线段等于已知线段·过一点作已知直线的垂线■尺规作图公法以下是尺规作图中可用的基本方法，也称为作图公法，任何尺规作图的步骤均可分解为以下五种方法：·通过两个已知点可作一直线。

·已知圆心和半径可作一个圆。

·若两已知直线相交，可求其交点。

正五边形的画法
步骤：
（1）先由一点出发，任意画两条长度相等的线段，使其夹角为108°。

（2）再从这两条线段的两个端点出发，向内画两个108°的角，使所画线段与前两条相等。

（3）最后，连接所剩的两个端点，即可。

正六边形的画法
步骤：
（1）先由一点出发，任意向右画两条长度相等的线段，使其夹角为120°。

（2）再从这两条线段的两个端点出发，向右画两个120°的角，使所画线段与前两条相等。

（3）再从这两个端点出发，向里画两个120°的角，两条射线相交点可用。

多余部分摖掉即可。

正八边形的画法
步骤：
（1）先由一点出发，任意向右画两条长度相等的线段，使其夹角为135°。

（2）再从这两条线段的两个端点出发，向右向内画两个135°的角，使所画线段与前两条相等。

（3）再从这两个端点出发，向里画两个135°的角，使两条射线通过截取与前四条相等。

（4）以此类推，从两个端点出发，画两个135°的角。

所画两条射线必然相交于一点。

多余部分摖掉即可。

正七边形的画法
步骤：。

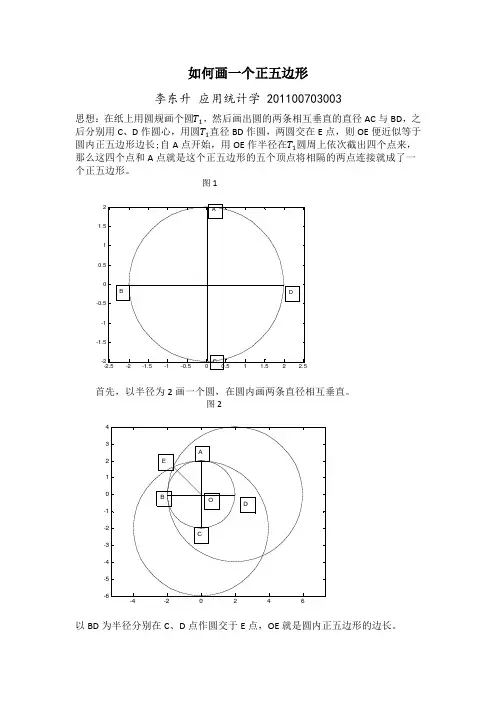
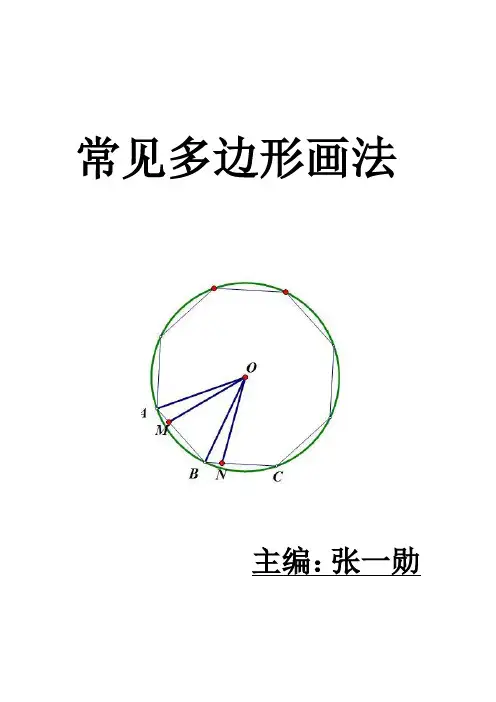
常见多边形画法主编：张一勋正三角形：以已知线段作正三角形1，如下图所示,分别以A，B两端为圆心，AB长为半径画圆，两圆交与C,D两点。

2，如下图所示，任选C或D分别于A,B两点相连，则有正三角形ABC或ABD。

正五边形：（1）近似画法①作线段AB等于定长l,并分别以A,B为圆心,已知长l为半径画弧与AB的中垂线交于K。

②以K为圆心，取AB的2/3长度为半径向外侧取C点，使CK=2/3AB。

③以点C为圆心，已知边长AB为半径画弧，分别与前两弧相交于M，N。

④顺次连接A，B，N，C，M各点即近似作得所要求的正五边形。

(2) 圆内接正五边形的尺规作法①以O为圆心,定长R为半径画圆,并作互相垂直的直径MN和AP。

②平分半径ON,得OK=KN。

③以点K为圆心,KA为半径画弧与OM交于点H，AH即为正五边形的边长。

④以AH为弦长,在圆周上截得A,B,C,D,E各点,顺次连接这些点即得正五边形。

(3)民间口诀画正五边形口诀介绍：“九五顶五九,八五两边分”。

画法:①画线段AB=20mm。

②作线段AB的垂直平分线，垂足为G。

③在l上连续截取GH，HD，使GH=5.9/5*10mm=19mm，HD=5.9/5*10mm=11.8mm。

④过H作EC⊥CG,在EC上截取HC=HE=8/5*10mm=16mm。

⑤连结DE，EA，EC，BC，CD。

五边形ABCDE就是边长为20mm的近似正五边形。

正六边形：画一个圆，做其一条直径。

以直径的两个端点为圆心，以已做圆的半径为半径分别画圆，做出4个交点，依顺序联结这4个点和直径的两个端点就可以。

正七边形的画法如下：（1）①以定长R为半径作圆，并过圆心O作互相垂直的纵横两条直径MN、HP.②过N点任作一射线NS，用圆规取七等分，把端点T与M连结起来，然后过NT上的各点推出MT的平行线，把MN七等分.③以M为圆心，MN为半径画弧，和PH的延长线相交于K点，从K向MN上各分点中的偶数点或奇数点（图中是1、3、5、7各点）引射线，与交于A、B、C、M.再分别以AB、BC、CM为边长，在圆周上从A点（或M点）开始各截一次，得到其他三点，把这些点依次连结起来，即得近似的正七边形.（2）另一种做法1、画一个圆，并且画一条任意半径。

数学为专业课服务：正五边形画法给工艺美术班授课时，发现有部分学生绘画五角星歪歪扭扭，不对称，不像五角星，为此，我再给他们进行“画正五边形”的辅导工作，诸如此类问题，再如，汽修班的机械制图课，有关投影问题、椭圆的画法等等，如果在数学教学中，如果注意结合生活实际、专业课要求等方面来改进课堂教学内容，学生的在课堂教学中会学有所获。

我国民间有口诀:九五顶五九,八五分两边.依照这个口诀.画边长20MM 的正五边形,在下面画法中填空.画法:1.画线段AB,使AB=( )2.作直线L 垂直且平分线段AB.垂足为G3.在L 上连续截取GH,HD,使GH=( )MM,HD=( ) MM4.过H 做EC 垂直DG 于H,在EC 上截取HC=HE=( )MM5.连接DE,EA,AB,BC,CD,五边形ABCDE 就是边长为20MM 的近似正五边形1.画线段AB,使AB=(20)2.作直线L 垂直且平分线段AB.垂足为G3.在L 上连续截取GH,HD,使GH=10*55.9=(19)，MM,HD=10*59.5=(11.8) MM4.过H 做EC 垂直DG 于H,在EC 上截取HC=HE=10*58(16)MM5.连接DE,EA,AB,BC,CD,五边形ABCDE 就是边长为20MM 的近似正五边形求sin18sin(3*18)=cos(2*18)3sin18-4(sin18)^3=1-2(sin18)^2设x=sin184x^3-2x^2-3x+1=04(x^3-x^2)+2(x^2-x)-(x-1)=0(x-1)(4x^2+2x-1)=0x1=1,x2=(-√5-1)/4,x3=(√5-1)/40<sin18<1sin18=(√5-1)/4几何方法:作等腰三角形ABC,∠A=36,则∠B=∠C=72作∠C平分线CD,交AB于D,作AH⊥BC于H则易知∠CAH=18,AD=CD=BC设BC=1,AC=AB=xBD/AD=BC/ACBD/1=1/x,BD=1/xAB=AD+BD,x=1+1/xx^2-x-1=0,x=(1±√5)/2∴AC=(1+√5)/2sin18=sin∠CAH=CH/AC=(1/2)/[(1+√5)/2]=(√5-1)/4求sin36 °解作黄金△ABC，∠BAC=36 °，∠ABC=∠ACB=72 °.令BC=a,AB=AC=b。