高一数学新教材人教版必修一第三章函数的概念与性质测试卷含答案

word

- 1 - / 10 第三章单元测试卷 一、单项选择题(本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中只有一个是符合题目要求的)

1．函数f(x)＝x－1x－2的定义域为( )

A．(1，＋∞) B．[1，＋∞)

C．[1,2) D．[1,2)∪(2，＋∞)

2．德国数学家狄利克雷在数学上做出了名垂史册的重大贡献，函数D(x)＝ 0，x∉Q1，x∈Q是以他名字命名的函数，则D(D(π))＝( )

A．1 B．0

C．πD．－1

3．已知f(x)是偶函数，g(x)是奇函数，且f(x)＋g(x)＝2x2－2x＋1，则f(－1)＝( )

A．3 B．－3

C．2 D．－2

4．若函数y＝f(x)的定义域是[0,2]，则函数g(x)＝f－x2x＋1的定义域是( )

A．[－4,0] B．[－4,0)

C．[－4，－1)∪(－1,0] D．(－4,0)

5．若幂函数y＝(m2－3m＋3)xm－2的图象不过原点，则m的取值X围为( )

A．1≤m≤2 B．m＝1或m＝2

C．m＝2 D．m＝1

6．已知函数f(x)是定义在R上的偶函数，x≥0时，f(x)＝x2－2x，则函数f(x)在R上的解析式是( )

A．f(x)＝－x(x－2) B．f(x)＝x(|x|－2)

C．f(x)＝|x|(x－2) D．f(x)＝|x|(|x|－2)

7．已知函数f(x)＝ x2＋1，x≤0，1，x>0，若f(x－4)>f(2x－3)，则实数x的取值X围是( )

A．(－1，＋∞) B．(－∞，－1) word

- 2 - / 10 C．(－1,4) D．(－∞，1)

8．甲、乙二人从A地沿同一方向去B地，途中都使用两种不同的速度v1与v2(v1

二、多项选择题(本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分)

2020年新高一数学必修一知识点总结

第三章函数的概念与性质

3.1函数的概念及其表示1.函数是刻画变量间对应关系的数学模型和工具。

2.函数问题的共同特征：定义域、值域均为非空数集；定义域和值域间有一

个对应关系；对于定义域中的任何一个自变量，在值域中都有唯一确定的数

与之对应。3.函数中的对应关系可用解析式、图象、表格等表示，为了表示方便，引进符号

f统一表示对应关系。

【注】函数符号

yfx是由德国数学家莱布尼茨在18世纪引入的。

4.函数定义

一般地，设,AB是非空的实数集，如果对于集合A中的任意一个数x，按

照某种确定的对应关系f，在集合B中都有唯一确定的数y和它对应，那么就

称:fAB为从集合A到集合B的一个函数，记作

,yfxxA。

其中，x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对

应的y值叫做函数值，函数值的集合fxxA叫做函数的值域。

5.函数的三要素：定义域；对应关系；值域。

6.（1）函数的定义域和对应关系可以确定出函数的值域，即一个函数的值域是

由它的定义域和对应关系决定的。

（2）没有特别说明的情况下，函数的定义域默认是使其有意义的自变量取值范

围。如yx，则默认定义域是

0xx（3）实际问题中的函数定义域要根据实际情况定.

如：匀速直线运动中位移、速度和时间的关系：

stvt,隐含着0t。

6.几个特殊函数的定义域和值域

（1）正比例函数

0ykxk，定义域和值域都为全体实数R。

（2）一次函数

0ykxbk，定义域和值域都为全体实数R。

（3）反比例函数

0k

yk

x，定义域为

0xx，值域为

0yy。

（4）一元二次函数20yaxbxca，定义域为R。

当0a

时，值域为24

4acb

yy

a







；

当0a

时，值域为24

4acb

yy

a







。7.区间及其表示

设,ab是两个实数，且ab（注意：a不能等于b）。我们规定：

人教版高一数学必修一第三单元《函数概念与性质》

单元练习题（含答案）

一、单选题

1．设2yxx，则0,1x上的最大值是（ ）

A．0 B．14 C．12 D．14

2．下列图象中表示函数图象的是（ ）

A． B．

C． D．

3．下列哪个函数的定义域与函数12xy的值域相同（ ）

A．2xy B．1yxx C．12yx D．lnyxx

4．已知函数()fx是定义域为R的奇函数，当0x时，2()ln1fxxx，则不等式(21)(1)fxf的解集为( )

A．{|0}xx B．{|0}xx C．{|1}xx D．{|1}xx

5．已知圆221xy及以下三个函数：（1）3fxx；（2）cosfxxx；（3）tanfxx.其中图象能等分圆的面积的函数个数为（ ）

A．3 B．2 C．1 D．0 6．已知函数12(log)yfx的定义域为11,42，则函数(2)xyf的定义域为（ ）

A．1,0 B．0,2 C．1,2 D．0,1

7．下列各组函数中，表示同一函数的是（ ）

A．y＝1，yxx B．y＝x2，y＝（x+1）2

C．y＝x，y33x D．y＝|x|，y2()x

8．函数315xfxx的定义域为（ ）

A．3, B．3,44,

C．3, D．3,4

9．已知23fxx，45gxx，则使得fhxgx成立的hx（ ）

A．23x B．211x C．24x D．45x

10．设函数fxx，则函数21fxfx的最大值为（ ）.

A．12 B．12 C．34 D．1

11．已知2()sinlg(1)4,fxaxbxxabR，且3[lg(log10)]5f，则[lg(lg3)]f( )

【创优单元测评卷】高中人教A版数学必修1单元测试：第一章会合与函数观点(二)B卷(含答案分析)

高中同步创优单元测评

B 卷

数 学

班级：

________ 姓名：

________

得分： ________

第一章

会合与函数观点

(二 )

( 函数的观点与基天性质 )

名校好题 ·能力卷 ]

( 时间： 120 分钟 满分： 150 分 )

第Ⅰ卷 ( 选择题 共60分)

一、选择题 (本大题共 12 个小题， 每题 5 分，共 60 分，在每题给出的四个选项中，

只有一项为哪一项切合题目要求的 )

1．以下四组函数中，表示同一函数的是 ( )

A ． y＝ x－ 1 与 y＝－ 2

B ． y＝ x－ 1与 y＝ x－ 1

x－ 1

2

C． y＝ 4lg x 与 y＝2lg x

x

D ． y＝ lg x － 2 与 y＝ lg100 2

A 中的元素个数最 2．已知 f： x→x 是会合 A 到会合 B＝ {0,1,4} 的一个映照，则会合

多有()

A．3 个 B．4 个

C．5 个 D．6 个

x＋ 1的定义域是 ( )

3．函数 f(x) ＝ x－ 1

A ．－ 1,1) B ．－ 1,1)∪ (1，＋ ∞)

C．－ 1，＋ ∞) D． (1，＋ ∞)

4．函数 y＝ 2－ － x2＋ 4x的值域是 ( )

A ．－ 2,2] B ．1,2]

C． 0,2] D．－ 2， 2]

5．已知 f(x) 的图象如图，则 f(x) 的分析式为 ( ) 【创优单元测评卷】高中人教A版数学必修1单元测试：第一章会合与函数观点(二)B卷(含答案分析)

1， 0≤ x≤1

A ． f(x) ＝ － x－ 2， 1

2

人教A版必修一第三章函数的概念与性质单元测试试卷

本试卷满分100分，考试时间80分钟．

命题人：高雪伟

一、单项选择题（本大题共5小题，每小题5分，共计25分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上）

1．函数()yfx的定义域为[﹣1，2]，则函数(1)(1)yfxfx的定义域为

A．[﹣1，3] B．[0，2] C．[﹣1，1] D．[﹣2，2]

2．已知函数2()(2)21fxmxmx的值域是[0，)，则实数m的取值范围是

A．[﹣2，2] B．[﹣1，2]

C．[﹣2，﹣1][2，) D．(，﹣1][2，)

3．已知函数321()(1)mfxmmx是幂函数，对任意的1x，2x(0，)且1x≠2x，满足1212()()0fxfxxx，若a，bR，a＋b＜0，则()()fafb的值

A．恒大于0 B．恒小于0 C．等于0 D．无法判断

4．已知函数()fx是定义在R上的偶函数，且对1x，2x(0，)(1x≠2x)，都有221[()xfx

21212()]()xfxxx＜0．记(1)af，(2)4fb，(3)9fc，则

A．a＜c＜b B．a＜b＜c C．b＜c＜a D．c＜b＜a

5．已知定义在R上的奇函数()yfx，当x≥0时，22()fxxaa，若对任意实数x有()()fxafx成立，则正数a的取值范围为

A．(0，14] B．(0，12] C．[14，) D．[12，)

1 单元素养检测(二)(第三章)

(120分钟 150分)

一、单项选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求的)

1．已知函数f(x)由下表给出，则f[f(3)]等于( )

x 1 2 3 4

f(x) 2 3 4 1

A．1 B．2 C．3 D．4

【解析】选A.因为f(3)＝4，所以f[f(3)]＝f(4)＝1.

2．函数f(x)在区间[－2，5]上的图象如图所示，则此函数的最小值、最大值分别是( )

A．－2，f(2) B．2，f(2)

C．－2，f(5) D．2，f(5)

【解析】选C.由函数最值的几何意义知，当x＝－2时，有最小值－2；当x＝5时有最大值f(5).

3．已知f(x)是一次函数，且f(x－1)＝3x－5，则f(x)的解析式为( )

A．f(x)＝3x＋2 B．f(x)＝3x－2

C．f(x)＝2x＋3 D．f(x)＝2x－3

【解析】选B.设f(x)＝kx＋b(k≠0)，

所以f(x－1)＝k(x－1)＋b＝3x－5，

即kx－k＋b＝3x－5，

所以k＝3，b－k＝－5， 解得k＝3，b＝－2，

所以f(x)＝3x－2.

4．下列各组函数中，表示同一函数的是( )

A．f(x)＝x＋1 x－1 ，g(x)＝x2－1

B．f(x)＝x2 ，g(x)＝(x )2 2 C．f(x)＝x2－1x－1 ，g(x)＝x＋1

D．f(x)＝x2，g(x)＝3x6

【解析】选D.A.f(x)的定义域为[1，＋∞)，g(x)的定义域为(－∞，－1]∪[1，＋∞)，故不是同一函数；

B．f(x)的定义域为R，g(x)的定义域为[0，＋∞)，故不是同一函数；

C．f(x)的定义域为{x|x≠1}，g(x)的定义域为R，故不是同一函数；

D．f(x)的定义域为R，g(x)的定义域为R，且两函数解析式化解后为同一解析式．

第1页，共6页 新人教A版必修第一册单元测试卷

第三章 函数的概念与性质

本试卷共6页, 22小题。全卷满分150分。考试用时120分钟。

★祝考试顺利★

注意事项：

1. 答题前, 先将自己的姓名、准考证号填写在试卷和答题卡上, 并将准考证号条形码粘贴在答题卡上的指定位置。

2. 选择题的作答：每小题选出答案后, 用2B铅笔把答题卡上对应题目的答案标号涂黑。写在试卷、草稿纸和答题卡上的非答题区域均无效。

3. 非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内。写在试卷、草稿纸和答题卡上的非答题区域均无效。

4. 考试结束后, 将本试卷和答题卡一并上交。

一、单项选择题：本题共8小题, 每小题5分, 共40分。在每小题给出的四个选项中, 只有一项是符合题目要求的。

1. 如图所示的4个图象中, 与所给3个事件最吻合的顺序为

(1)我离开家后, 心情愉悦, 缓慢行进, 但最后发现上学快迟到了, 加速前进；

(2)我骑着自行车上学, 但中途车坏了, 我修理好又以原来的速度前进；

(3)我快速地骑着自行车去上学, 最后发现时间充足, 又减缓了速度.

① ② ③ ④

A. ③①② B. ③④② C. ②①③ D. ②④③

2. 下列函数是奇函数的是

A. 35()fxxxx B. 2()1fxx C. ()1fxx D. 2(),[1,3]fxxx

3. 函数1()12fxxx的定义域为

A. [1,2)(2,+) B. (1,) C. [1,2) D. [1,) 离开家的距离时间O离开家的距离时间O离开家的距离时间O离开家的距离时间O第2页，共6页 4. 已知幂函数()fxx的图象过点(2,2), 则下列说法正确的是

人教A版（2019）高中数学必修第一册

第三章 函数概念与性质 函数的概念【附答案】

一、选择题（60分）

1．函数(1)yxxx的定义域为（ ）

A．|0xx B．|1xx C．|10xx D．|01xx

2．已知函数()(0)1xafxxax，若210ax，则()fx的取值范围是（ ）

A．[21,1) B．(22,1) C．[22,1) D．(2,0)

3．函数y2019xx2018的值域是（ ）

A．0,2 B．0,2 C．1,2 D．1,2

4．函数11yxx的值域为

A．[1, 2] B．[1,2] C．[ 262,2] D．[2,2]

5．已知函数242txtfxx在区间［－1,2］上的最大值为2，则t的值等于（ ）

A．2或3 B．－1或3 C．1 D．3

6．设函数2()(0)fxaxbxca的定义域为D，若所有点构成一个正方形区域，则a的值为（ ）

A．2 B．4 C． D．8

7．已知定义在0,上的函数fx满足2fxfxx，且当0,2x时,8fxx，则93f（ ）.

A．2019 B．2109 C．2190 D．2901

8．记号[x]表示不超过实数x的最大整数，若2()[30]30xfxx，则1232930fffff的值为（ ）

A．899 B．900 C．901 D．902

9．函数21222fxxxxx的最大值为（ ）．

A．2 B．32 C．52 D．2

10．设D是含数1的有限实数集，()fx是定义在D上的函数，若()fx的图象绕原点逆吋针旋转3后与原图象重合，则在以下各项中(1)f的取值只可能是

一、选择题

1．已知mR，若函数||xmfxe对任意xR满足20212120fxfx，则不等式1lnln2fxfex的解集是（ ）

A．1,,ee B．1,ee

C．10,,ee D．,e

2．已知函数xxfxee，则不等式2210fxfx成立的一个充分不必要条件为（ ）

A．2,1 B．0,1 C．1,12 D．1,1,2

3．已知幂函数()(1)nfxax的图象过点(2,8)，且(2)(12)fbfb，则b的取值范围是（ ）

A．(0,1) B．(1,2) C．(,1) D．(1,)

4．已知函数2265mmmfxx是幂函数，对任意1x，20,x，且12xx，满足12120fxfxxx，若a，bR，且0ab，则fafb的值（ ）

A．恒大于0 B．恒小于0 C．等于0 D．无法判断

5．已知幂函数2242()(1)mmfxmx在(0,)上单调递增，函数()2xgxt，任意1[1,6)x时，总存在2[1,6)x使得12fxgx，则t的取值范围是（ ）

A．128t B．128t C．28t或1t D．28t或1t

6．已知函数2()fxxbxc，且(2)()fxfx，则下列不等式中成立的是（ ）

A．(4)(0)(4)fff B．(0)(4)(4)fff

C．(0)(4)(4)fff D．(4)(0)(4)fff

7．我国著名数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休.”在数学的学习和研究中，常用函数的图像来研究函数的性质，也常用函数的解析式来琢磨函数图像的特征.我们从这个商标中抽象出一个图象如图，其对应的函数可能是（ ）

一、选择题

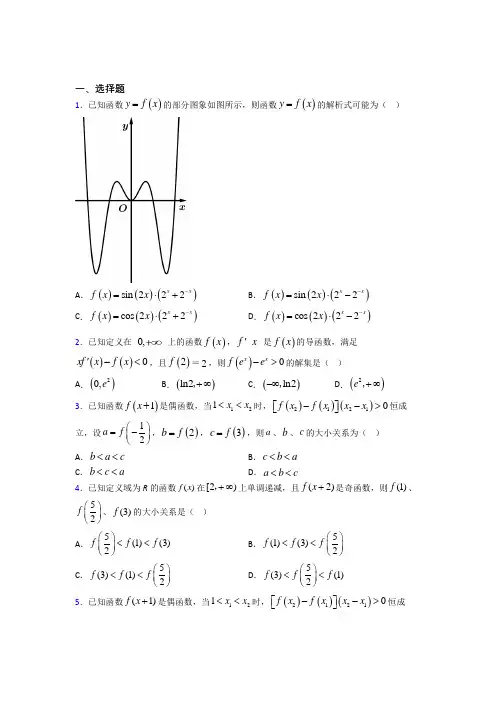
1．已知函数yfx的部分图象如图所示，则函数yfx的解析式可能为（ ）

A．sin222xxfxx B．sin222xxfxx

C．cos222xxfxx D．cos222xxfxx

2．已知定义在0,上的函数fx，fx是fx的导函数，满足0xfxfx，且2f＝2，则0xxfee的解集是（ ）

A．20,e B．ln2, C．ln2, D．2e,

3．已知函数1fx是偶函数，当121xx时，21210fxfxxx恒成立，设12af，2bf，3cf，则a、b、c的大小关系为（ ）

A．bac B．cba

C．bca D．abc

4．已知定义域为R的函数()fx在[2)，上单调递减，且(2)fx是奇函数，则(1)f、52f、(3)f的大小关系是（ ）

A．5(1)(3)2fff B．5(1)(3)2fff

C．5(3)(1)2fff D．5(3)(1)2fff

5．已知函数(1)fx是偶函数，当121xx时，21210fxfxxx恒成立，设1,(2),(3)2afbfcf，则,,abc的大小关系为（ ）

A．bac B．cba C．bca D．abc

6．已知幂函数()(1)nfxax的图象过点(2,8)，且(2)(12)fbfb，则b的取值范围是（ ）

A．(0,1) B．(1,2) C．(,1) D．(1,)

7．若定义在R的奇函数fx在,0单调递减，则不等式20fxfx的解集为（ ）

一、选择题

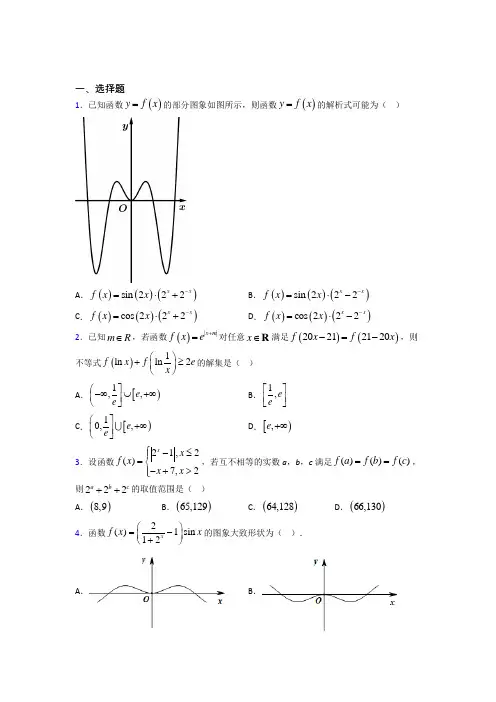
1．已知函数yfx的部分图象如图所示，则函数yfx的解析式可能为（ ）

A．sin222xxfxx B．sin222xxfxx

C．cos222xxfxx D．cos222xxfxx

2．已知mR，若函数||xmfxe对任意xR满足20212120fxfx，则不等式1lnln2fxfex的解集是（ ）

A．1,,ee B．1,ee

C．10,,ee D．,e

3．设函数21,2()7,2xxfxxx，若互不相等的实数a，b，c满足()()()fafbfc，则222abc的取值范围是（ ）

A．8,9 B．65,129 C．64,128 D．66,130

4．函数2()1sin12xfxx的图象大致形状为（ ）．

A． B． C． D．

5．已知定义在R上的偶函数()fx满足：当0x时，()2xfx，且(2)(3)fxafx对一切xR恒成立，则实数a的取值范围为（ ）

A．1,32 B．1,32 C．[32,) D．(0,32]

6．奇函数()fx在(0)，内单调递减且(2)0f，则不等式(1)()0xfx的解集为（ ）

A．,21,02, B．2,12,

C．,22, D．,21,00,2

7．已知定义在R上的函数fx，满足3fmnfmfn，且0x时，3fx，则下列说法不正确的是（ ）

A．6fxfx

一、选择题

1．已知函数yfx的部分图象如图所示，则函数yfx的解析式可能为（ ）

A．sin222xxfxx B．sin222xxfxx

C．cos222xxfxx D．cos222xxfxx

2．已知mR，若函数||xmfxe对任意xR满足20212120fxfx，则不等式1lnln2fxfex的解集是（ ）

A．1,,ee B．1,ee

C．10,,ee D．,e

3．已知函数(1)fx是偶函数，当121xx时，21210fxfxxx恒成立，设1,(2),(3)2afbfcf，则,,abc的大小关系为（ ）

A．bac B．cba C．bca D．abc

4．已知奇函数fx在区间2,3上单调递增，则fx在区间3,2上（ ）

A．单调递增，且最大值为2f B．单调递增，且最大值为3f

C．单调递减，且最大值为2f D．单调递减，且最大值为3f

5．已知函数(1)fx为偶函数，()fx在区间[1,)上单调递增，则满足不等式(21)(3)fxfx的x的解集是（ ）

A．31,5 B．3(,1),5 C．1(,1),5 D．11,5

6．已知fx是定义在R上的奇函数，若12,xxR，且12xx，都有12120xxfxfx成立，则不等式2120xfxx的解集是（ ）

A．,11,2 B．0,11,

C．,01,2 D．0,12,

第1页共4页最新人教版高中数学必修一第三章试卷（含答案）

第三章函数的概念与性质

一、单选题1．下列函数是奇函数的是（）

A．B．C．D．

2．幂函数的图象经过点，则的值为（）

A．1B．-1C．0D．2

3．已知函数是定义在R上偶函数，且在内是减函数，若，则满足的实数x的取值范围为（）A．B．

C．D．

4．设函数的定义域为，有下列三个命题，这些命题中，真命题的个数是（）①若存在常数，使得任意，有，则是函数的最大值②若存在，使得对任意，且，有，则是函数的

最大值③若的最大值为2，则的最大值也为2A．0个B．1个C．2个D．3个

5．函数，，则的值域为（）

A．B．

C．D．

6．已知是定义在上的偶函数，且在区间单调递减，则不等式

的解集为（）第2页共4页A．B．C．D．

二、多选题7．已知函数，下列说法正确的是（）

A．函数的图象的对称中心是（0，1）B．函数在R上是增函数

C．函数是奇函数D．方程的解为

8．已知偶函数满足，在区间上，下列

判断正确的是（）A．B．在上是减函数

C．函数在处取得最大值D．函数没有最小值

三、填空题9．函数的值域是_________．

10．若函数，则__________.

11．已知函数，若对，不等式恒成立，则实数的取

值范围是______.12．已知函数，，若在区间上的最大值是3，则的

取值范围是______.

四、解答题13．已知实数是常数，函数.求函数的定义域，

判断函数的奇偶性，并说明理由.

高中数学必修一第三章函数的概念与性质必须掌握的典型题

单选题

1、若函数𝑓(

𝑥)

=𝑥𝛼

的图象经过点(9,1

3)，则𝑓(1

9)=（ ）

A．1

3B．3C．9D．8

答案：B

分析：将(9,1

3)代入函数解析式，即可求出𝛼，即可得解函数解析式，再代入求值即可.

解：由题意知𝑓(

9)

=1

3，所以9𝛼

=1

3，即32𝛼

=3−1

，

所以𝛼=−1

2，所以𝑓(

𝑥)

=𝑥−1

2，所以𝑓(1

9)=(1

9)−1

2

=3.

故选：B

2、已知函数𝑓(

𝑥)

的定义域为(

3,5)

，则函数𝑓(

2𝑥+1)

的定义域为（ ）

A．(

1,2)

B．(

7,11)

C．(

4,16)

D．(

3,5)

答案：A

分析：根据3<2𝑥+1<5求解即可

∵𝑓(

𝑥)

的定义域为(

3,5)

，∴3<𝑥<5，由3<2𝑥+1<5，得1<𝑥<2，则函数𝑓(

2𝑥+1)

的定义域为(

1,2)

故选：A.

3、函数𝑓(

𝑥)

=𝑥2

−1的单调递增区间是（ ）

A．(

−∞,−3)

B．[

0,+∞)

C．(

−3,3)

D．(

−3,+∞)

答案：B

分析：直接由二次函数的单调性求解即可.

由𝑓(

𝑥)

=𝑥2

−1知，函数为开口向上，对称轴为𝑥=0的二次函数，则单调递增区间是[

0,+∞)

.

故选：B.

4、已知函数𝑓(

𝑥)

是定义在R上的偶函数，𝑓(

𝑥)

在[

0,+∞)

上单调递减，且𝑓(

3)

=0，则不等式(

2𝑥−5)

𝑓(

𝑥−

1)

<0的解集为（ ） A．(−2,5

2)∪(

4,+∞)

B．(

4,+∞)

C．(

−∞,−2)

∪[5

2,4]D．(

−∞,−2)

答案：A

分析：根据偶函数的性质及区间单调性可得(−∞,0)上𝑓(𝑥)单调递增且𝑓(−3)=𝑓(3)=0，进而确定𝑓(𝑥)的区

间符号，讨论{2𝑥−5>0

𝑓(𝑥−1)<0

、{2𝑥−5<0

𝑓(𝑥−1)>0

求解集即可.

由题设，(−∞,0)上𝑓(𝑥)单调递增且𝑓(−3)=𝑓(3)=0，

答卷时应注意事项

１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，

有什么题型，哪些容易，哪些难，做到心里有底；

３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到

暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应

该多读几遍，比如从小到大，从左到右这样的题；

４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手

臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏

的小题；

５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读

题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的

答题；

６、卷面要清洁，字迹要清工整，非常重要；

７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检

查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判

断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，

认真答题，相信你一定会闯关成功。相信你是最棒的！第三章单元测试卷

班级：___________姓名：___________

评卷人得分

一、单选题（每题５分，共40分）

1．已知幂函数

yfx=

的图象过点

2,2，则

4f=（ ）

A．2-B．2C．1D．4

2．某人去上班，先跑步，后步行.如果y表示该人离单位的距离，x表示出发后的时间，那么下列图象中符合

此人走法的是（ ）.

A．B．

C．D．

3．下列四个函数中，在(0,)+¥上为增函数的是（ ）

A．()3fxx=-B．2()3

fxxx=-C．1

()fx

x=D．()fxx=

4．下列哪组中的两个函数是同一函数（ ）

一、选择题

1．已知函数fx为定义在R上的奇函数，当0x时，(1)lnfxx，则1f（ ）

A．ln2 B．ln2 C．0 D．1

2．已知0.31()2a，12log0.3b，0.30.3c，则abc，，的大小关系是（ ）

A．abc B．cab C．acb D．bca

3．已知2xfxx，,Mabab，4,NyyfxxM∣，则使得MN的实数对,ab有（ ）

A．0个 B．1个 C．2个 D．3个

4．已知函数xxfxee，则不等式2210fxfx成立的一个充分不必要条件为（ ）

A．2,1 B．0,1 C．1,12 D．1,1,2

5．奇函数()fx在(0)，内单调递减且(2)0f，则不等式(1)()0xfx的解集为（ ）

A．,21,02, B．2,12,

C．,22, D．,21,00,2

6．意大利著名天文学家伽利略曾错误地猜测链条自然下垂时的形状是抛物线．直到1690年，雅各布·伯努利正式提出该问题为“悬链线”问题并向数学界征求答案．1691年他的弟弟约翰·伯努利和菜布尼兹、惠更斯三人各自都得到了正确答案，给出悬链线的数学表达式——双曲余弦函数：()coshxfxcaca2xxaaeea（e为自然对数的底数）．当0c，1a时，记(1)pf，12mf，(2)nf，则p，m，n的大小关系为（ ）．

A．pmn B．nmp C．mpn D．mnp

7．设函数fx的定义域为R，112fxfx，当0,1x时，1fxxx.若存在,xm，使得364fx有解，则实数m的取值范围为（ ）