21数列基础

考点21 数列的综合应用【高考再现】热点一、等差数列与等比数列的综合应用1．（2012年高考（陕西理））设{}n a 的公比不为1的等比数列,其前n 项和为n S ,且534,,a a a 成等差数列.(1)求数列{}n a 的公比; (2)证明:对任意k N +∈,21,,k k k S S S ++成等差数列.2．（2012年高考（福建文））在等差数列{}n a 和等比数列{}n b 中,{}1141,8,n a b b a ===的前10项和1055S =. (Ⅰ)求n a 和n b ;(Ⅱ)现分别从{}n a 和{}n b 的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率.3．（2012年高考（天津文））(本题满分13分)已知{}n a 是等差数列,其前n 项和为n S ,{}n b 是等比数列,且114444,27,=10a b a b S b =+=-. (I)求数列{}n a 与{}n b 的通项公式; (II)记1122=+++n n n T a b a b a b (*n N ∈)证明:*118(,2)n n n T a b n N n ---=∈>.4．（2012年高考（湖北文））已知等差数列{}n a 前三项的和为3-,前三项的积为8.(1) 求等差数列{}n a 的通项公式;(2)若231,,a a a 成等比数列,求数列{}n a 的前n 项和.5．．（2012年高考（天津理））已知{n a }是等差数列,其前n 项和为n S ,{n b }是等比数列,且1a =1=2b ,44+=27a b ,44=10S b -.(Ⅰ)求数列{n a }与{n b }的通项公式; (Ⅱ)记1121=+++n n n n T a b a b a b -,+n N ∈,证明+12=2+10n n n T a b -+()n N ∈.【方法总结】对等差、等比数列的综合问题的分析，应重点分析等差、等比数列的通项及前n 项和；分析等差、等比数列项之间的关系．往往用到转化与化归的思想方法．热点二、数列与其他章节知识的综合应用 1．（2012年高考（四川文））设函数3()(3)1f x x x =-+-,{}n a 是公差不为0的等差数列,127()()()14f a f a f a ++⋅⋅⋅+=,则=++721a a a （ ）A ．0B ．7C ．14D ．21.2．（2012年高考（上海文））若)(sin sin sin 7727*∈+++=N n S n n πππ ,则在10021,,,S S S 中,正数的个数是 （ ） A ．16.B ．72.C ．86.D ．100.3．（2012年高考（湖北文））定义在(,0)(0,)-∞⋃+∞上的函数()f x ,如果对于任意给定的等比数列{}{},()n n a f a 仍是等比数列,则称()f x 为“保等比数列函数”.现有定义在(,0)(0,)-∞⋃+∞上的如下函数:①2()f x x =;②()2xf x =;③()||f x x =;④()ln ||f x x =. 则其中是“保等比数列函数”的()f x 的序号为（ ） A ．①② B ．③④ C ．①③ D ．②④.【答案】C【解析】设数列{}n a 的公比为q .对于①,22112()()n n n nf a a q f a a ++==,是常数,故①符合条件;对于②,111()22()2n n n n a a a n a n f a f a ++-+==,不是常数,故②不符合条件;对于③,11||()()||n n n n a f a f a a ++=1n n a q a +==,是常数,故③符合条件;对于④, 11()ln ||()ln ||n n n n f a a f a a ++=,不是常数,故④不符合条件.由“保等比数列函数”的定义知应选C.4．（2012年高考（福建文））数列{}n a 的通项公式cos2n n a n π=,其前n 项和为n S ,则2012S 等于（ ） A ．1006B ．2012C ．503D ．05．（2012年高考（北京文））某棵果树前n 年得总产量n S 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为 （ ）A ．5B ．7C ．9D ．11【答案】C【解析】由图可知6,7,8,9这几年增长最快,超过平均值,所以应该加入, 因此选C.6．（2012年高考（上海文））已知xx f +=11)(.各项均为正数的数列}{n a 满足11=a ,)(2n n a f a =+.若20122010a a =,则1120a a +的值是_________.7．（2012年高考（四川文））已知a 为正实数,n 为自然数,抛物线22na y x =-+与x 轴正半轴相交于点A ,设()f n 为该抛物线在点A 处的切线在y 轴上的截距. (Ⅰ)用a 和n 表示()f n ; (Ⅱ)求对所有n 都有()1()11f n nf n n -≥++成立的a 的最小值; (Ⅲ)当01a <<时,比较111(1)(2)(2)(4)()(2)f f f f f n f n ++⋅⋅⋅+---与 )1()0()1()1(6f f n f f -+-⋅的大小,并说明理由.8．（2012年高考（湖南文））某公司一下属企业从事某种高科技产品的生产.该企业第一年年初有资金2000万元,将其投入生产,到当年年底资金增长了50%.预计以后每年资金年增长率与第一年的相同.公司要求企业从第一年开始,每年年底上缴资金d 万元,并将剩余资金全部投入下一年生产.设第n 年年底企业上缴资金后的剩余资金为a n 万元. (Ⅰ)用d 表示a 1,a 2,并写出1n a 与a n 的关系式;(Ⅱ)若公司希望经过m (m ≥3)年使企业的剩余资金为4000万元,试确定企业每年上缴资金d 的值(用m 表示).9．（2012年高考（四川理））已知a 为正实数,n 为自然数,抛物线22na y x =-+与x 轴正半轴相交于点A ,设()f n 为该抛物线在点A 处的切线在y 轴上的截距. (Ⅰ)用a 和n 表示()f n ;(Ⅱ)求对所有n 都有33()1()11f n n f n n -≥++成立的a 的最小值;(Ⅲ)当01a <<时,比较11()(2)nk f k f k =-∑与27(1)()4(0)(1)f f n f f --的大小,并说明理由.10．（2012年高考（上海理））对于数集},,,,1{21n x x x X -=,其中n x x x <<<< 210,2≥n ,定义向量集},),,(|{X t X s t s a a Y ∈∈==. 若对于任意Y a ∈1,存在Y a ∈2,使得021=⋅a a ,则称X具有性质P. 例如}2,1,1{-=X 具有性质P. (1)若x >2,且},2,1,1{x -,求x 的值;(2)若X 具有性质P,求证:1∈X ,且当x n >1时,x 1=1;(3)若X 具有性质P,且x 1=1, x 2=q (q 为常数),求有穷数列n x x x ,,,21 的通项公式.11．（2012年高考（大纲理））函数2()23f x x x =--.定义数列{}n x 如下:112,n x x +=是过两点(4,5),(,())n n n P Q x f x 的直线n PQ 与x 轴交点的横坐标.(1)证明:123n n x x +≤<<; (2)求数列{}n x 的通项公式.【方法总结】1．解决此类问题要抓住一个中心——函数，两个密切联系：一是数列和函数之间的密切联系，数列的通项公式是数列问题的核心，函数的解析式是研究函数问题的基础；二是方程、不等式与函数的联系，利用它们之间的对应关系进行灵活的处理．2．从近几年新课标高考试题可以看出，不同省市的高考对该内容要求的不尽相同，考生复习时注意把握．数列与解析几何交汇问题主要是解析几何中的点列问题，关键是充分利用解析几何的有关性质、公式，建立数列的递推关系式，然后借助数列的知识加以解决．【考点剖析】一．明确要求1．熟练把握等差数列与等比数列的基本运算．2．掌握隐藏在数列概念和解题方法中的数学思想，如“函数与方程”、“数形结合”、“分类讨论”、“等价转化”等．3．注意总结相关的数列模型以及建立模型的方法．二．命题方向1．考查数列的函数性及与方程、不等式、解析几何相结合的数列综合题．2．考查运用数列知识解决数列综合题及实际应用题的能力．三．规律总结基础梳理1．等比数列与等差数列比较表不同点相同点等差数列(1)强调从第二项起每一项与前项的差；(2)a1和d可以为零；(3)等差中项唯一(1)都强调从第二项起每一项与前项的关系；(2)结果都必须是同一个常数；(3)数列都可由a1，d或a1，q确定等比数列(1)强调从第二项起每一项与前项的比；(2)a1与q均不为零；(3)等比中项有两个值2.解答数列应用题的步骤(1)审题——仔细阅读材料，认真理解题意．(2)建模——将已知条件翻译成数学(数列)语言，将实际问题转化成数学问题，弄清该数列的特征、要求是什么．(3)求解——求出该问题的数学解．(4)还原——将所求结果还原到原实际问题中．3．数列应用题常见模型(1)等差模型：如果增加(或减少)的量是一个固定量时，该模型是等差模型，增加(或减少)的量就是公差．(2)等比模型：如果后一个量与前一个量的比是一个固定的数时，该模型是等比模型，这个固定的数就是公比．(3)递推数列模型：如果题目中给出的前后两项之间的关系不固定，随项的变化而变化时，应考虑是a n与a n＋1的递推关系，还是S n与S n＋1之间的递推关系．一条主线数列的渗透力很强，它和函数、方程、三角形、不等式等知识相互联系，优化组合，无形中加大了综合的力度．解决此类题目，必须对蕴藏在数列概念和方法中的数学思想有所了解．两个提醒(1)对等差、等比数列的概念、性质要有深刻的理解，有些数列题目条件已指明是等差(或等比)数列，但有的数列并没有指明，可以通过分析，转化为等差数列或等比数列，然后应用等差、等比数列的相关知识解决问题．(2)数列是一种特殊的函数，故数列有着许多函数的性质．等差数列和等比数列是两种最基本、最常见的数列，它们是研究数列性质的基础，它们与函数、方程、不等式、三角等内容有着广泛的联系，等差数列和等比数列在实际生活中也有着广泛的应用，随着高考对能力要求的进一步增加，这一部分内容也将受到越来越多的关注．三种思想(1)数列与函数方程相结合时主要考查函数的思想及函数的性质(多为单调性)．(2)数列与不等式结合时需注意放缩．(3)数列与解析几何结合时要注意递推思想．【基础练习】1．（经典习题）某学校高一、高二、高三共计2 460名学生，三个年级的学生人数刚好成等差数列，则该校高二年级的人数是( )A．800 B．820 C．840 D．8602．(教材习题改编)有一种细菌和一种病毒，每个细菌在每秒钟杀死一个病毒的同时将自身分裂为2个，现在有一个这样的细菌和100个这样的病毒(假设病毒不繁殖)，问细菌将病毒全部杀死至少需要 ( ) A ．6秒钟 B ．7秒钟 C ．8秒钟D ．9秒钟3．（经典习题）若a ，b ，c 成等比数列，则函数y ＝ax 2＋bx ＋c 的图象 与x 轴的交点的个数为( ) A ．0 B ．1 C ．2D ．不能确定【解析】：由题意b 2＝ac (ac ＞0)，∴Δ＝b 2－4ac ＝－3b 2＜0. 【答案】： A4．（经典习题）5·12汶川大地震后，山东天成书业公司于2008年8月向 北川中学捐赠《三维设计》系列丛书三万册，计划以后每年比上一年多捐5 000册，则截至到2012年，这5年共捐________万册．【解析】：由题意知a 1＝3，d ＝0.5 S 5＝3×5＋5×42×0.5＝20. 【答案】205．（经典习题）一个凸多边形的内角成等差数列，其中最小的内角为2π3，公差为π36，则这个多边形的边数为________．6．(人教A版教材习题改编)已知等差数列{a n}的公差为2，若a1，a3，a4成等比数列，则a2的值为()．A．－4 B．－6 C．－8 D．－10【解析】由题意知：a23＝a1a4.则(a2＋2)2＝(a2－2)(a2＋4)，解得：a2＝－6.【答案】 B7．（经典习题）已知数列{a n}是各项均为正数的等比数列，数列{b n}是等差数列，且a6＝b7，则有()．A．a3＋a9≤b4＋b10B．a3＋a9≥b4＋b10C．a3＋a9≠b4＋b10D．a3＋a9与b4＋b10的大小关系不确定8．（经典习题）若互不相等的实数a，b，c成等差数列，c，a，b成等比数列，且a＋3b＋c＝10，则a＝()．A．4 B．2 C．－2 D．－4【名校模拟】一．基础扎实1．(2012云南省第一次高中毕业生统一检测复习文)已知n S 是等比数列{}n a 的前n 项和，1a 与3a 的等差中项等于15. 如果4120S =，那么2012200920093S S -= （A ）18 （B ）25 （C ）32 （D ）392．(2012年云南省第一次统一检测理)在等比数列{}n a 中，6a 与7a 的等差中项等于48，610987654128=a a a a a a a . 如果设{}n a 的前n 项和为n S ，那么=n S（A ）45-n（B ）34-n（C ）23-n（D ）12-n【解析】：设等比数列{}n a 的公比为q ，由已知得⎩⎨⎧=+=96)1(1285164271q q a q a ，化简得 ⎩⎨⎧=+=96)1(251661q q a q a ，解得⎩⎨⎧==211q a . ∴12-=n n S .选（D ）.3．(湖北武汉2012毕业生五月供题训练（三）文)一个样本容量为10的样本数据，它们组成一个公差不为O 的等差数列{n a }，若a 3 =8，且a 1，a 3，a 7成等比数列，则此样本的平均数和中位数分别是A ．13 ,12B ．13 ,13C ．12 ,13D ．13 ,14．4．(仙桃市2012年五月高考仿真模拟试题文)已知x x f 2sin )(=，若等差数列}{n a 的第5项的值为)6('πf ，则=+++18899221a a a a a a a a 。

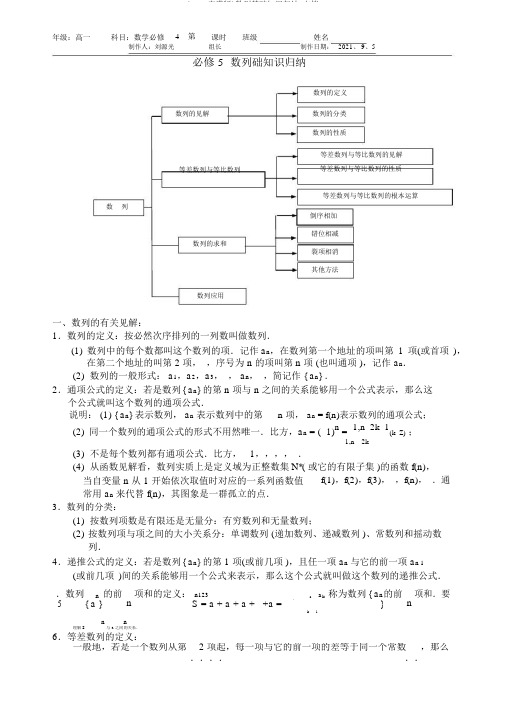
年级：高一科目：数学必修4第课时班级姓名制作人：刘源光组长制作日期：2021、 9、5必修 5数列础知识归纳数列的定义数列的见解数列的分类数列的性质等差数列与等比数列的见解等差数列与等比数列等差数列与等比数列的性质等差数列与等比数列的根本运算数列倒序相加错位相减数列的求和裂项相消其他方法数列应用一、数列的有关见解：1．数列的定义：按必然次序排列的一列数叫做数列．(1) 数列中的每个数都叫这个数列的项．记作a n，在数列第一个地址的项叫第1 项(或首项)，在第二个地址的叫第 2 项，，序号为 n 的项叫第 n 项 (也叫通项 )，记作 a n．(2)数列的一般形式： a1，a2，a3，， a n，，简记作 { a n} ．2．通项公式的定义：若是数列{ a n} 的第 n 项与 n 之间的关系能够用一个公式表示，那么这个公式就叫这个数列的通项公式．说明： (1) { a n} 表示数列， a n表示数列中的第n 项， a n = f(n)表示数列的通项公式；(2)同一个数列的通项公式的形式不用然唯一．比方，a n = ( 1)n = 1,n 2k 1(k Z)；1,n 2k(3)不是每个数列都有通项公式．比方， 1，，，，．(4)从函数见解看，数列实质上是定义域为正整数集N*( 或它的有限子集 )的函数 f(n)，当自变量 n 从 1 开始依次取值时对应的一系列函数值常用 a n来代替 f(n)，其图象是一群孤立的点．f(1)，f(2)，f(3)，，f(n)，．通3．数列的分类：(1)按数列项数是有限还是无量分：有穷数列和无量数列；(2)按数列项与项之间的大小关系分：单调数列 (递加数列、递减数列 )、常数列和摇动数列．4．递推公式的定义：若是数列{ a n} 的第 1 项(或前几项 )，且任一项 a n与它的前一项 a n 1 (或前几项)间的关系能够用一个公式来表示，那么这个公式就叫做这个数列的递推公式．．数列n的前n 项和的定义： n123n ak称为数列{ a n的前n项和．要n5{ a }S = a + a + a + +a =}k1n n理解 S与 a 之间的关系．6．等差数列的定义：一般地，若是一个数列从第 2 项起，每一项与它的前一项的差等于同一个常数，那么．．．．．．这个数列就叫等差数列，这个常数叫做等差数列的公差，公差平时用字母 d 表示．．即：{ a n为等比数列n + 1n n + 1n n + 2n n2 }a a = d 2a= a + a a = kn + b S = An + Bn 7．等比数列的定义：一般地，若是一个数列从第 2 项起，每一项与它的前一项的比等于同一个常数，那么．．．．．．这个数列就叫做等比数列，这个常数叫做等比数列的公比．公比平时用字母 q 表示 (q0)，即： { a n} 为等比数列a n + 1： a n = q (q0)2a n a n 2 ．a n 1注意条件“从第 2 项起〞、“常数〞q．由定义可知：等比数列的公比和项都不为零．二、等差、等比数列的性质：等差数列 (AP)等比数列 (GP)通项公式a n1n1n 11，= a + (n 1)d a = a q (a 0 q 0)n(a1a n )n(n 1) d na1 , q1,前 n 项和S n na1S n a1 (1 q n ), q 1.221q①a n = a m + (n m)d②m + n = s + t，那么 a m + a n =a s + a t性质③S m，2m m， 3m2m，成S S S SAP①a n = a m q n m②m + n = s + t，那么 a m n s ta = a a③S m，2m m， 3m2m，成GP S S S S(q 1 或 m 不为偶数 )④a k，k + m，k + 2m，成AP，d④ak，k + m，k + 2m，成maa= md aa GP，q = q 注： 1．等差 (等比 )数列 { a n} 的任意等距离的项组成的数列仍为等差(等比 )数列．2．三个数成等差的想法：a d，a，a + d；四个数成等差的想法： a 3d，a d，a + d， a + 3d；，，；四个数成等比的错误想法：3，a/q，aq，aq3(为3．三个数成等比的想法： a/q a aq a/q 什么？ )nc a n(c > 0)是等比数列．4．{ a } 为等差数列，那么5．{ b n} ( b n > 0)是等比数列，那么 {log c b n } ( c > 0 且 c 1) 是等差数列．6．公差为 d 的等差数列 { a n} 中，假设 d > 0，那么 { a n} 是递加数列；假设 d = 0，那么 { a n} 是常数列；假设 d < 0，那么 { a n} 是递减数列．7．等比数列 { a n} 中，假设公比为 q，那么(1) 当 a1 > 0，q > 1 或 a1 < 0，0 < q < 1 时为递加数列；(2) 当 a1 < 0，q > 1 或 a1 > 0，0 < q < 1 时为递减数列；(3) 当 q < 0 时为摇动数列；(4) 当 q = 1 时为常数列．8．等差数列前 n 项和最值的求法：(1)a1 > 0， d < 0 时， S n有最大值； a1 < 0， d > 0 时， S n有最小值．(2)S n最值的求法：①假设 S n，可用二次函数最值的求法 (n N*) ；②假设 a n，那么n取最值时n 的值(n N*)能够下确定：n 最大值a n0(或n 最小S S Sa n 10值 a n0)．a n10三、常有数列通项的求法：1．定义法 (利用 AP，GP 的定义 )．2．累加法 (a n + 1a n = c n型)：a n = a1 + (a2 a1) + (a3 a2) + + (a n a n 1) = a1 + c1 + c2 ++ c n 1(n2)．3．公式法： a nS 1 (n 1) ．S nS n 1 (n 2)4．累乘法 (an 1c n 型 )：a n = a 1a 2 a 3 L a n = a 1c 1c 2c n1(n2)．a n= qaa 1 a 2 a n 10)型，转变为 a + x = q(a + x)．可5．待定系数法： a+ b (q 0，q 1，bn + 1 nn + 1n 以将其改写变形成以下形式： a n + 1 + b = q(a n + b )，于是可依据等比数列的定义求出其通项公式．q 1q 1 6．间接法 (比方： a n + 1 a n = 4a n + 1a n1 14 )．a n 1a n四、数列的求和方法： 除化归为等差数列或等比数列求和外，还有以下一些常用方法：1．拆项求和法 (a= bnc )：将一个数列拆成假设干个简单数列(如等差数列、等比数列、nn常数数列等等 )，尔后分别求和．如 n n ． a = 2n + 32．并项求和法：将数列的相邻两项 (或假设干项 )并成一项 (或一组 )先求和，尔后再求 S n ．如“S n12 22 32 42 52 62 L(2 n 1)2 (2 n)2 〞的求和．= f(n + 1)f(n)，使得正3．裂项相消法：将数列的每一项拆 (裂开 )成两项之差，即 an负项能互相抵消， 剩下首尾假设干项． 用裂项相消法求和， 需要掌握一些常有的裂项，如： a n( An 1C ) C 1 ( 1 1 C ) 、 1 = 1 1 、 1 1 ( ab) 等． B )( An B An B An n(n 1) n n 1 a b a b4．错位相减法：将一个数列的每一项都作相同的变换，尔后将获取的新数列错动一个地址与原数列的各项相减， 这是模拟推导等比数列前 n 项和公式的方法． 对一个由等差数列及等比数列对应项之积组成的数列的前 n 项和，常用错位相减法． 即错位相减法一般只要求解决下述数列的求和：假设 a n = b n c n ，其中 { b n } 是等差数列， { c n } 是等比数列，那么数列 { a n } 的求和运用错位相减法． 记 S n1 12 23 3+n n ，那么 n1 22 3+n 1 n n n + 1= b c + b c + b c + b c qS = b c + b c + b c + b c ， 如 a n = (2n 1) 2n ．5．倒序相加法：将一个数列的倒数第 k 项(k = 1，2，3， ， n)变为顺数第 k 项，尔后将获取的新数列与原数列相加，这是模拟推导等差数列前 n 项和公式的方法． 注意： (1) “数列求和〞是数列中的重要内容，在中学高考范围内，学习数列求和不需 要学习任何理论，上面所述求和方法可是将一些常用的数式变换技巧运用于数列求和 之中．(2) “错位〞与“倒序〞求和的方法是比较特其他方法．(3) 数列求通项及和的方法多种多样，要视详尽状况采纳合适的方法．(4) 重要公式：① 1 + 2 + + n = 1 ； ② 22 + 2 1 33+ 2 n(n + 1)1 +2 + n = 6 n(n + 1)(2n + 1)；③ 1 + 2 +n 3 = (1 + 2 + + n)2 = 1 n 2(n + 1)2；4* ④ 等差数列中， S m + n* ⑤ 等比数列中， S m + n= S m + S n + mnd ；= S n + q n S m = S m + q mS n ． ab(1 b)n五、分期付款(按揭贷款 )：每次还款x(1b)n 1元(贷款 a 元，n 次还清，每期利率为 b)．。

【高频考点解读】1.了解数列的概念和几种简单的表示方法（列表、图象、通项公式）．2.了解数列是自变量为正整数的一类函数．【热点题型】题型一由数列的前几项求数列的通项例1、写出下面各数列的一个通项公式:(1)3，5,7，9，…;（2)错误!，错误!,错误!，错误!，错误!，…;(3）－1,错误!，－错误!，错误!，－错误!，错误!，…;（4）3，33，333,3333，….解(1）各项减去1后为正偶数,所以a n＝2n＋1.（2）每一项的分子比分母少1，而分母组成数列21，22，23,24，…，所以a n＝错误!.（3)奇数项为负，偶数项为正,故通项公式中含因子（－1)n;各项绝对值的分母组成数列1，2，3,4，…；而各项绝对值的分子组成的数列中,奇数项为1，偶数项为3,即奇数项为2－1,偶数项为2＋1，所以a n＝(－1）n·错误!。

也可写为a n＝错误!(4）将数列各项改写为错误!，错误!，错误!，错误!，…，分母都是3，而分子分别是10－1，102－1，103－1，104－1，…，所以a n＝错误!（10n－1)．【提分秘籍】根据所给数列的前几项求其通项时，需仔细观察分析，抓住其几方面的特征:分式中分子、分母的各自特征；相邻项的联系特征；拆项后的各部分特征；符号特征，应多进行对比、分析，从整体到局部多角度观察、归纳、联想．【举一反三】（1）数列－1，7，－13,19,…的一个通项公式是a n＝________。

（2）数列｛a n}的前4项是错误!,1,错误!，错误!,则这个数列的一个通项公式是a n＝________。

答案(1)(－1)n·(6n－5）(2）错误!解析（1）符号问题可通过（－1）n或(－1)n＋1表示,其各项的绝对值的排列规律为后面的数的绝对值总比前面的数的绝对值大6，故通项公式为a n＝(－1）n（6n－5)．（2）数列｛a n}的前4项可变形为错误!，错误!，错误!,错误!，故a n＝错误!。

2021高考数学数列数列是数学中的重要概念之一，也是高考数学考查的重点内容之一。

在2021年的高考数学考试中，数列仍然是必考的知识点。

本文将围绕2021高考数学数列展开讨论，从数列的定义、分类、性质以及解题方法等方面进行分析和总结，帮助考生更好地掌握数列相关知识，为高考取得优异成绩提供帮助。

一、数列的定义和分类数列是按照一定规律排列的一组数的集合。

通常用数学公式表示为{a₁, a₂, a₃, ...}，其中a₁, a₂, a₃, ...是数列的项。

数列可以分为等差数列和等比数列两大类。

等差数列是指数列中相邻两项之差保持恒定的数列。

例如，{1, 3, 5, 7, 9, ...}就是一个等差数列，其中公差为2。

等比数列是指数列中相邻两项之比保持恒定的数列。

例如，{2, 4, 8, 16, 32, ...}就是一个等比数列，其中公比为2。

二、数列的性质数列具有一些重要的性质，掌握这些性质对于解题非常有帮助。

1. 公差/公比的性质：对于等差数列，任意两项的差等于公差；对于等比数列，任意两项的比等于公比。

2. 通项公式：数列中的每一项可以通过通项公式来表示。

对于等差数列，通项公式为an=a₁+(n-1)d；对于等比数列，通项公式为an=a₁r^(n-1)，其中an表示第n项，a₁表示首项，d表示公差，r表示公比。

3. 前n项和公式：数列的前n项和表示为Sn=a₁+a₂+...+an。

对于等差数列，前n项和公式为Sn=(a₁+an)n/2；对于等比数列，前n项和公式为Sn=a₁(1-r^n)/(1-r)。

三、数列的解题方法解题时，需要根据题目给出的条件来确定数列的类型，然后利用数列的性质进行分析和计算。

1. 求第n项：如果已知数列的通项公式，可以通过将n代入公式中计算出第n项的值。

2. 求前n项和：如果已知数列的通项公式，可以通过将n代入前n 项和公式中计算出前n项和的值。

3. 求公差/公比：如果已知数列的前几项，可以利用这些项之间的关系来求出公差或公比。

数列基础知识梳理一、数列1、 数列的定义数列是按照一定顺序排列着的一列数，在函数的意义下，数列是某一定义域为正整数或它的有限子集{1,2,3,4，……，n}的函数，即当自变量从小到大依次取值时对应的一列函数值，其图像是无限个或有限个孤立的点，数列的一般形式为123,,,,,,n a a a a 通常简记为{}n a ，其中n a 是数列的第n 项，也叫通项。

注意：1）{}n a 与n a 是不同的概念，{}n a 表示数列123,,,,,,n a a a a 而n a 表示的是这个数列的第n 项2）数列与集合的区别集合中元素性质：确定性，无序性，互异性；数列中数的性质：确定性，有序性，可重复性。

2、 数列的通项公式当一个数列{}n a 的第n 项n a 与项数n 之间的函数关系可以用一个公式()n a f n =来表示，就把这个公式叫数列{}n a 的通项公式，可根据数列的通项公式算出数列的各项，也可判断给定的数是否为数列{}n a 中的项或可确定是第几项。

但不是所有数列都可以写出通项公式，数列的通项公式也不唯一。

3、 数列的表示方法数列看成一个特殊的函数，所有从函数的观点出发，数列的表示方法有以下三种：1）解析法:通项公式和递推公式两种；2）列表法3）图像法（数列的图像是一系列孤立的点）4、 数列的分类(1)有穷数列和无穷数列(2)单调数列，搬动数列，常数列5、 等差数列1）定义：一般地，如果一个数列从第2项起，每一项与它前一项的差等于同一个常数，这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差通常用字母d 表示定义的表示为：*n-1(n N ,n 2)n a a d -=∈≥或者*1n (n N )n a a d +-=∈ 公差d 可正可负或为零，为零时，数列为常数列。

2）等差数列的通项公式对于第二个公式要求,n m a a 是数列中的项即可，也可表示为3）等差数列的增减性4）等差中项任意两个数,a b 有且仅有一个等差中项，即2a b A +=。

2。

1 数列1.设A、B是两个集合，按照某一法则f,对于集合A中的每一个元素,集合B中都有唯一确定的元素和它对应,那么，法则f叫做集合A到集合B的映射。

2。

设函数f（x）＝x(x∈R）,则函数f(x）的图象是一条直线。

3.设函数f（x）＝x(x∈N＊),则函数f（x）的图象是一系列的点，它们分布在第一象限,且位于直线y＝x上.4.设函数f（n)＝错误!(n∈N＊），则函数f(n）的图象是分布在函数f(x）＝错误!(x＞0)的图象上的一系列的点.5。

记a n＝错误!（n∈N*)，则a n就是以n为自变量的函数，若将n＝1，2，3,4,…的函数值一一列出，这样的一列数就是一个数列.6.按照一定次序排列的一列数叫做数列。

7。

数列1,错误!,错误!，错误!，错误!,…中，错误!是数列中的第4项,这个数4就称为项数,该数列中项数是5的项是错误!。

8.数列a1，a2，a3，a4…，a n,…，简记为{a n｝,其中排在数列第一位的数a1称为数列的首项，a n是数列中的第n项,称为数列的通项.9。

项数有限的数列叫做有穷数列,项数无限的数列叫做无穷数列。

10。

如果a n＋1＞a n(n＜∈N*），则该数列为单调递增数列.11。

如果数列的每一项都是同一个常数,这样的数列叫做常数列。

12.数列｛a n}的第n项a n与项数n之间的关系可以用一个公式来表示，这个公式叫做数列的通项公式.13。

数列与函数的关系:数列可以看作以正整数集N＊（或它的有限子集｛1，2，…,k}）为定义域的函数,当自变量从小到大依次取值时所对应的一列函数值14。

数列的表示方法.（1）数列的表示方法：通项公式法、列表法、图象法.(2）数列可用图象来表示，在平面直角坐标系中,以序号n为横坐标,相应的项a n为纵坐标描点画图,其图象是一些孤立的点，它们位于第一象限或第四象限或x轴的正半轴.15。

数列单调性的判断,依据a n＋1与a n的大小,当a n＋1＞a n时，为递增数列;当a n＋1＜a n 时，为递减数列。

第二十一讲数列的概念【复习目标】数列的定义和通项公式。

正确利用数列的递推关系解答数列问题。

【基础知识回顾】一、数列的概念1、数列的定义数列是按照一定的次序排成的一列数，从函数观点看，数列是定义域为的函数f(n),当自变量n从1开始依次取正整数时所对应的一列函数值f(1),f(2),…,f(n), ….2、数列的通项公式一个数列{an }的第n项an与之间的函数关系，如果可以用一个公式an=f(n)来表示，这个公式叫做这个数列的通项公式。

二、数列的分类1、按照项数是有限还是无限分：、。

2、按照项与项的大小关系分：、、、。

三、an 与Sn的关系设数列{an }前n项和Sn=a1+a2+a3+…+an,则an=四、几点小提示：1、数列与数集应予以区别，数列中的数列排列有序，数集中的数排列有序，数集中的元素无序；数列中的数可重复出现，数集中的元素互异。

2、并不是每一个数列都有通项公式，给出前n项时，写出的通项公式可以不止一个。

3、已知{an }的前n项和Sn求an时，用an=求解应注意分类讨论。

a n=Sn -S1n-是在n≥2条件下求出的，应检验a1是否适合。

如果适合，则合写在一块，如果不适合，则分段表示。

【基础知识自测】1、数列 ,924,715,58,1的一个通项公式n a 是（ ）A 、122+n nB 、1)2(++n n nC 、)1(21)1(2+-+n n D 、12)2(++n n n2、已知数列}{n a 的通项公式是132+=n na n ，那么这个数列是（ ） A 、递增数列 B 、递减数列 C 、摆动数列 D 、常数列3、已知数列前n 项和+∈+-=N n n n S n ,1322则它的通项公式是 。

4、已知数列}{n a 满足n a a a n n +==+11,0，则=2009a 。

5、如果数列}{n a 的前n 项和为323-=n n a S ，则这个数列的通项公式是 。