4.5_指数与对数函数(复习课)
- 格式:ppt
- 大小:1.16 MB
- 文档页数:23

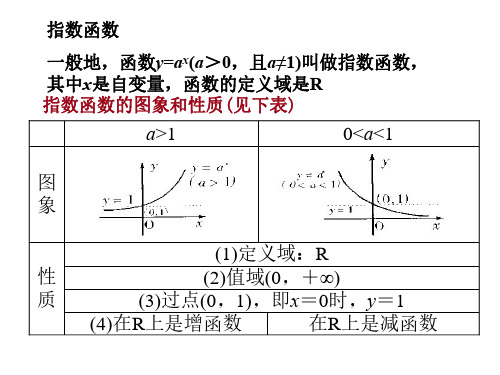
指数与指数函数基础梳理1.分数指数幂(1)规定:正数的正分数指数幂的意义是a mn =na m (a >0,m ,n ∈N *,且n >1);正数的负分数指数幂的意义是a -mn =1n a m(a >0,m ,n ∈N *,且n >1);0的正分数指数幂等于0;0的负分数指数幂没有意义.(2)有理指数幂的运算性质:a r a s =a r +s , (a r )s =a rs , (ab )r =a r b r , 其中a >0,b >0,r ,s ∈Q . 2.指数函数的图象与性质y =a xa >10<a <1图象定义域 R 值域(0,+∞) 性质过定点(0,1)当x >0时,y >1; 当x <0时,0<y <1 当x >0时,0<y <1;当x <0时,y >1在(-∞,+∞)上是增函数在(-∞,+∞)上是减函数对数与对数函数基础梳理1.对数的概念(1)对数的定义:如果N a b =(a >0且a ≠1),那么数b 叫做以a 为底N 的对数,记作Na b log =,其中a 叫做对数的底数,N 叫做真数. (2)几种常见对数对数形式 特点记法 一般对数 底数为a (a >0且a ≠1)log a N 常用对数 底数为10 lg N 自然对数底数为eln N2.对数的性质与运算法则(1)对数的性质 (对数恒等式) ①N aNa =log ;②b ba a=log (a >0且a ≠1).(2)对数的运算法则:如果a >0且a ≠1,M >0,N >0,那么①log a (MN )=log a M +log a N ;②log a MN =log a M -log a N ;③log a M n =n log a M (n ∈R ); (3)对数的换底公式abNbNalog log log =(a ,b 均大于零且不等于1); 推论:a bba log 1log = ;b a b an m m n log log = ; da d c cb b a log log log log =⋅⋅.3.对数函数的图象与性质xa y log =a >1 0<a <1图象性质定义域:(0,+∞)值域:R过点(1,0)当x >1时,y >0;当0<x <1,y <0 当x >1时,y <0;当0<x <1时,y >0是(0,+∞)上的增函数是(0,+∞)上的减函数4.反函数:指数函数y =a x 与对数函数xa y log =互为反函数,它们的图象关于直线y =x 对称.练习检测1.(2011·某某)若点(a,9)在函数y =3x 的图象上,则tan a π6的值为( ).A .0 B.33C .1 D. 3解析 由题意有3a =9,则a =2,∴tan a π6=tan π3= 3. 答案 D2.(2012·某某五校联考)函数f (x )=2|x -1|的图象是( ).解析 f (x )=⎩⎪⎨⎪⎧2x -1,x ≥1,⎝ ⎛⎭⎪⎫12x -1,x <1,故选B.答案 B3.若函数f (x )=12x +1,则该函数在(-∞,+∞)上是( ).A .单调递减无最小值B .单调递减有最小值C .单调递增无最大值D .单调递增有最大值 解析 设y =f (x ),t =2x +1, 则y =1t ,t =2x +1,x ∈(-∞,+∞)t =2x +1在(-∞,+∞)上递增,值域为(1,+∞). 因此y =1t 在(1,+∞)上递减,值域为(0,1). 答案 A4.(2011·某某)已知a =4.32log 5,b =6.34log 5,c =3.03log 51⎪⎭⎫⎝⎛,则( ).A .a >b >cB .b >a >cC .a >c >bD .c >a >b解析 c =⎝ ⎛⎭⎪⎫15log 30.3=5-log 30.3=5log 3103,log 23.4>log 22=1,log 43.6<log 44=1,log 3103>log 33=1,又log 23.4>log 2103>log 3103,∴log 2 3.4>log 3103>log 4 3.6 又∵y =5x 是增函数,∴a >c >b . 答案 C5.(2012·某某一中月考)已知32121=+-aa ,则a +a -1=______;a 2+a -2=________.解析 由已知条件(a 12+a -12)2=9.整理得:a +a -1=7 又(a +a -1)2=49,因此a 2+a -2=47. 答案 7 476.化简下列各式(其中各字母均为正数). (1)65312121132)(b a ba b a ⋅⋅---;(2)21332121231)4()3(65----⋅÷-⋅⋅b a b a b a .[审题视点] 熟记有理数指数幂的运算性质是化简的关键.解 (1)原式=a -13b 12·a -12b 13a 16b 56=a -13-12-16·b 12+13-56=1a . (2)原式=-52a -16b -3÷(4a 23·b -3)12 =-54a -16b -3÷⎝ ⎛⎭⎪⎫a 13b -32 =-54a -12·b -32 =-54·1ab3=-5ab 4ab 2.化简结果要求(1)若题目以根式形式给出,则结果用根式表示;(2)若题目以分数指数幂的形式给出,则结果用分数指数幂表示;(3)结果不能同时含有根号和分数指数幂,也不能既有分母又有负指数幂. 【训练1】 计算:(1)021231)12()972()71(027.0--+----;(2)213323121)(1.0)4()41(----⋅b a ab . 解 (1)原式=⎝ ⎛⎭⎪⎫271 000-13-(-1)-2⎝ ⎛⎭⎪⎫17-2+⎝ ⎛⎭⎪⎫25912-1=103-49+53-1=-45.(2)原式=412·432100·a 32·a -32·b 32·b -32=425a 0·b 0=425. 7.函数y =e x +e -xe x -e-x 的图象大致为( ).[审题视点] 函数图象的判断要充分利用函数的性质,如奇偶性、单调性.解析y =e 2x +1e 2x -1=1+2e 2x -1,当x >0时,e 2x -1>0且随着x 的增大而增大,故y =1+2e 2x -1>1且随着x 的增大而减小,即函数y 在(0,+∞)上恒大于1且单调递减,又函数y 是奇函数,故选A. 答案 A利用指数函数的图象和性质可研究复合函数的图象和性质,比如:函数y =a x -1a x +1,y=e x -e -x2,y =lg(10x -1)等.8. 已知方程10x =10-x ,lg x +x =10的实数解分别为α和β,则α+β的值是________.解析 作函数y =f (x )=10x ,y =g (x )=lg x ,y =h (x )=10-x 的图象如图所示,由于y =f (x )与y =g (x )互为反函数,∴它们的图象是关于直线y =x 对称的.又直线y =h (x )与y =x 垂直,∴y =f (x )与y =h (x )的交点A 和y =g (x )与y =h (x )的交点B 是关于直线y =x 对称的.而y =x 与y =h (x )的交点为(5,5).又方程10x=10-x 的解α为A 点横坐标,同理,β为B 点横坐标.∴α+β2=5,即α+β=10. 答案 109.(2011·某某五市模拟)设函数y =f (x )在(-∞,+∞)内有定义.对于给定的正数K ,定义函数f K (x )=⎩⎨⎧f (x ),f (x )≥K ,K ,f (x )<K ,取函数f (x )=2+x +e -x ,若对任意的x ∈(-∞,+∞),恒有f K (x )=f (x ),则K 的最大值为________.10. 若f 1(x )=3|x -1|,f 2(x )=2·3|x -a |,x ∈R ,且f (x )=⎩⎨⎧f 1(x ),f 1(x )≤f 2(x ),f 2(x ),f 1(x )>f 2(x ),则f (x )=f 1(x )对所有实数x 成立,则实数a 的取值X 围是________.1.已知a =log 0.70.8,b =log 1.10.9,c =1.10.9,则a ,b ,c 的大小关系是( ). A .a <b <c B .a <c <b C .b <a <c D .c <a <b解析 将三个数都和中间量1相比较:0<a =log 0.70.8<1,b =log 1.10.9<0,c =1.10.9>1. 答案 C2.(2012·黄冈中学月考)函数f (x )=log 2(3x +1)的值域为( ).A .(0,+∞)B .[0,+∞)C .(1,+∞)D .[1,+∞) 解析 设y =f (x ),t =3x +1. 则y =log 2t ,t =3x +1,x ∈R .由y =log 2t ,t >1知函数f (x )的值域为(0,+∞). 答案 A3.若1log 32>a ,则a 的取值X 围是________. 答案⎝ ⎛⎭⎪⎫23,14.求值:(1)log 89log 23;(2)(lg 5)2+lg 50·lg 2;(3)12lg 3249-43lg 8+lg 245.[审题视点] 运用对数运算法则及换底公式. 解 (1)原式=log 2332log 23=23.(2)原式=(lg 5)2+lg(10×5)lg 105=(lg 5)2+(1+lg 5)(1-lg 5)=(lg 5)2+1-(lg 5)2=1. (3)法一 原式=12(5lg 2-2lg 7)-43×32lg 2+12(2lg 7+lg 5) =52lg 2-lg 7-2lg 2+lg 7+12lg 5=12(lg 2+lg 5)=12lg 10=12. 法二 原式=lg 427-lg 4+lg(75)=lg 42×757×4=lg 10=12.对数源于指数,对数与指数互为逆运算,对数的运算可根据对数的定义、对数的运算性质、对数恒等式和对数的换底公式进行.在解决对数的运算和与对数的相关问题时要注意化简过程中的等价性和对数式与指数式的互化. 5. (1)若2a =5b =10,求1a +1b 的值. (2)若x log 34=1,求4x +4-x 的值. 解 (1)由已知a =log 210,b =log 510,则1a +1b =lg 2+lg 5=lg 10=1. (2)由已知x =log 43,则4x +4-x =4log 43+4-log 43=3+13=103.6.已知f (x )是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是增函数,设a =f (log 47),b =f (321log ),c =f (0.2-0.6),则a ,b ,c 的大小关系是( ).A .c <a <bB .c <b <aC .b <c <aD .a <b <c[审题视点] 利用函数单调性或插入中间值比较大小.解析 log 123=-log 23=-log 49,b =f (log 123)=f (-log 49)=f (log 49),log 47<log 49,0.2-0.6=⎝ ⎛⎭⎪⎫15-35=5125>532=2>log 49, 又f (x )是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是增函数,故f (x )在[0,+∞)上是单调递减的,∴f (0.2-0.6)<f (log 123)<f (log 47),即c <b <a ,故选B. 答案 B一般是同底问题利用单调性处理,不同底问题的处理,一般是利用中间值来比较大小,同指(同真)数问题有时也可借助指数函数、对数函数的图象来解决.7.(2010·全国)设a =log 32,b =ln 2,c =215-,则( ). A .a <b <c B .b <c <a C .c <a <b D .c <b <a解析 法一 a =log 32=1log 23,b =ln 2=1log 2e ,而log 23>log 2e >1,所以a <b ,c =5-12=15,而5>2=log 24>log 23,所以c <a ,综上c <a <b ,故选C.法二 a =log 32=1log 23,b =ln 2=1log 2e ,1<log 2e <log 23<2,∴12<1log 23<1log 2e <1;c =5-12=15<14=12,所以c <a <b ,故选C. 答案 C8.已知函数f (x )=)2(log ax a-,是否存在实数a ,使函数f (x )在[0,1]上是关于x 的减函数,若存在,求a 的取值X 围.[审题视点]a >0且a ≠1,问题等价于在[0,1]上恒有⎩⎨⎧a >12-ax >0.解 ∵a >0,且a ≠1,∴u =2-ax 在[0,1]上是关于x 的减函数. 又f (x )=log a (2-ax )在[0,1]上是关于x 的减函数,∴函数y =log a u 是关于u 的增函数,且对x ∈[0,1]时,u =2-ax 恒为正数. 其充要条件是⎩⎨⎧a >12-a >0,即1<a <2.∴a 的取值X 围是(1,2).研究函数问题,首先考虑定义域,即定义域优先的原则.研究复合函数的单调性,一定要注意内层与外层的单调性问题.复合函数的单调性的法则是“同增异减”.本题的易错点为:易忽略2-ax >0在[0,1]上恒成立,即2-a >0.实质上是忽略了真数大于0的条件. 9. 已知f (x )=log 4(4x -1) (1)求f (x )的定义域; (2)讨论f (x )的单调性;(3)求f (x )在区间⎣⎢⎡⎦⎥⎤12,2上的值域.解 (1)由4x -1>0解得x >0, 因此f (x )的定义域为(0,+∞). (2)设0<x 1<x 2,则0<4x 1-1<4x 2-1,因此log 4(4x 1-1)<log 4(4x 2-1),即f (x 1)<f (x 2),f (x )在(0,+∞)上递增. (3)f (x )在区间⎣⎢⎡⎦⎥⎤12,2上递增,又f ⎝ ⎛⎭⎪⎫12=0,f (2)=log 415,因此f (x )在⎣⎢⎡⎦⎥⎤12,2上的值域为[0,log 415].10.(2011·某某改编)设函数f(x)=⎩⎨⎧21-x ,x ≤1,1-log 2x ,x >1,则满足f(x)≤2的x 的取值X 围是________.。



高考总复习2025第5节 指数与对数运算课标解读1.通过对有理数指数幂、实数指数幂含义的认识,掌握指数幂的运算性质.2.理解对数的概念和运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数.3.能够利用指数与对数运算解决一些简单的实际问题.1 强基础 固本增分知识梳理1.指数及指数运算根式概念若一个(实)数x的n次方(n∈N,n≥2)等于a,即 ,则称x是a的n次方根性质当n是奇数时,数a的n次方根记作 ,正数的n次方根是一个 ,负数的n次方根是一个 当n是偶数时,正数a的n次方根有两个,它们互为 ,记作± (a>0),负数没有偶次方根0的n次方根是0x n=a正数 负数相反数实数指数幂有理指数幂的运算法则a r·a s= (a r)s= (ab)r= a>0,b>0,r,s∈Qa r+sa rs a rb r2.对数及对数运算概念性质底数的限制a>0,且a≠1对数式与指数式的互化:a b=N⇔ 负数和零没有对数1的对数是 :log a1= 底数的对数是 :log a a= 常用对数:lg N=log10N 自然对数l n N=log e N(e=2.718 28…)对数恒等式:B= 运算性质log a(M·N)= a>0,且a≠1,M>0,N>0 = log a M n= (n∈R)换底公式log a b= (a>0,且a≠1;c>0,且c≠1;b>0)0011Nlog a M+log a N log a M-log a Nn log a M如果 (a>0且a≠1),那么b叫作以a为底,(正)数N的对数,记作b= ,其中a叫作对数的 ,N叫作对数的 a b=Nlog a N 底数 真数b=log a N常用结论(a,b,c, d,a m均大于0且不等于1,n∈R).2.对数值的符号规律:log a b>0⇔(a-1)(b-1)>0,log a b<0⇔(a-1)(b-1)<0,其中a>0,a≠1,b>0.自主诊断题组一思考辨析(判断下列结论是否正确,正确的画“√”,错误的画“×”)2.log 2a 2=2log 2|a |.( )3.若M N >0,则log a (M N )=log a M+log a N (a >0,a ≠1).( )×√ × ×题组二回源教材5.(湘教版必修第一册习题4.1第10题改编)已知x>1,且x+x-1=3,则1 题组三连线高考7.(2021·天津,7)若2a=5b=10,则 =( )CA.-1B.lg 7C.1D.log7108.(2022·浙江,7)已知2a=5,log83=b,则4a-3b=( )C9.(2021·全国甲,理4)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录法的数据V满足L=5+lg V.已知某同学视力的五分记录法C的数据为4.9,则其视力的小数记录法的数据约为( ≈1.259)( ) A.1.5 B.1.2 C.0.8 D.0.62 研考点 精准突破考点一指数幂的运算10考点二 对数的运算(多考向探究预测)考向1对数式的化简与计算D-12考向2指数式与对数式的综合运算CA变式探究-1C考点三 指数与对数运算的实际应用例4(1)放射性核素锶89的质量M会按某个衰减率衰减,设初始质量为M0,质量M与时间t(单位:天)的函数关系为 (其中h为常数),若锶89的半衰期(质量衰减一半所用的时间)约为50天,那么质量为M0的锶89经过30天衰D减后质量大约变为( )(参考数据20.6≈1.516)A.0.72M0B.0.70M0C.0.68M0D.0.66M 0(2)(2024·湖南长沙模拟)二维码与我们的生活息息相关,我们使用的二维码主要是21×21大小的,即441个点.根据0和1的二进制编码规则,一共有2441种不同的码,假设我们1万年用掉3×1015个二维码,那么所有二维码大约可A以用( )(lg 2≈0.301,lg 3≈0.477)A.10117万年B.10118万年C.10119万年D.10200万年C。

指数函数与对数函数总结与练习一、指数的性质(一)整数指数幂n 1.整数指数幂概念:a =a ⋅Λ⋅a (n ∈N )a 0=1(a ≠0)1⋅4a 243*n 个aa-n=1a ≠0,n ∈N *)n(a 2.整数指数幂的运算性质:(1)a m ⋅a n =a m +n (m ,n ∈Z )(2)a (3)(ab )=a ⋅b n n n ()mn=a mn(m ,n ∈Z )(n ∈Z )其中a ÷a =a ⋅a m n m -n =a m -n a n ⎛a ⎫-1nn -n , ⎪=(a ⋅b)=a ⋅b =n .b ⎝b ⎭n 3.a 的n 次方根的概念即:若x n 一般地,如果一个数的n 次方等于a n >1,n ∈N ),那么这个数叫做a 的n 次方根,=a ,则x 叫做a 的n 次方根,(n >1,n ∈N )**(说明:①若n 是奇数,则a 的n 次方根记作n a ;若a >0则n a >0,若a <o 则n a <0;②若n 是偶数,且a >0则a 的正的n 次方根记作n a ,a 的负的n 次方根,记作:-n a ;(例如:8的平方根±8=±2216的4次方根±416=±2)③若n 是偶数,且a <0则n a 没意义,即负数没有偶次方根;④Θ0=0n >1,n ∈N nn (*)∴n 0=0;⑤式子a 叫根式,n 叫根指数,a 叫被开方数。
∴(a )nn=a ..4.a 的n 次方根的性质一般地,若n 是奇数,则n a n =a ;若n 是偶数,则n a n =a =⎨5.例题分析:例1.求下列各式的值:(1)3-8⎧a⎩-aa ≥0a <0.(3)(2)(-10)*2(3)4(3-π)(4)4例2.已知a <b <0,n >1,n ∈N ,化简:n (a -b )+n (a +b ).n n (二)分数指数幂1051231.分数指数幂:5a =a =a102(a >0)3a =a =a124(a >0)即当根式的被开方数能被根指数整除时,根式可以写成分数指数幂的形式;如果幂的运算性质(2)a 3()kn=akn 对分数指数幂也适用,442255⨯3⨯4⎛2⎫⎛⎫2532例如:若a >0,则 a 3⎪=a 3=a , a 4⎪=a 4=a ,∴a =a 3⎝⎭⎝⎭a =a .545即当根式的被开方数不能被根指数整除时,根式也可以写成分数指数幂的形式。
4.5。
2 用二分法求方程的近似解内容标准学科素养1.根据具体函数图象,能够借助计算器用二分法求相应方程近似解.数学运算数学抽象2.了解二分法的含义及近似思想、逼近思想及应用.授课提示:对应学生用书第71页[教材提炼]知识点二分法的概念及步骤错误!我们已经知道,函数f(x)=ln x+2x-6在区间(2,3)内存在一个零点.进一步的问题是,如何求出这个零点呢?取区间(2,3)的中点2.5,用计算工具算得f(2。
5)≈-0.084.因为f(2。
5)f(3)<0,那么零点在区间应该是哪个区间?知识梳理(1)对于在区间[a,b]上图象连续不断且f(a)f(b)<0的函数y=f(x),通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).(2)给定精确度ε,用二分法求函数y=f(x)零点x0的近似值的一般步骤如下:①确定零点x0的初始区间[a,b],验证f(a)f(b)<0.②求区间(a,b)的中点c。
③计算f(c),并进一步确定零点所在的区间:a.若f(c)=0(此时x0=c),则c就是函数的零点;b.若f(a)f(c)<0(此时x0∈(a,c)),则令b=c;c.若f(c)f(b)<0(此时x0∈(c,b)),则令a=c.④判断是否达到精确度ε:若|a-b|<ε,则得到零点近似值a (或b);否则重复步骤②~④.[自主检测]1.下列图象与x轴均有交点,其中不能用二分法求函数零点的是()答案:A2.用二分法求函数f(x)=log2x-32的零点时,初始区间可选为()A.(0,1)B.(1,2)C.(2,3) D.(3,4)答案:C3.用二分法求方程x3-2x-5=0在区间(2,3)内的实根,取区间中点为x0=2。
5,那么下一个有根的区间是________.答案:(2,2。
5)4.用二分法求函数y=f(x)在区间(2,4)上的近似解,验证f(2)·f(4)〈0,给定精确度ε=0。