二级倒立摆的二次型最优控制研究a

格式：pdf
大小：295.05 KB
文档页数：3

下载文档原格式

二级倒立摆系统的最优控制

J= 1 T T ∫ [ x (t )Qx(t ) + u (t ) Ru(t )]dt 20
∞
ut
+
B
+
1 /S
x
C
y
A
R-1BT
P
五、仿真分析
将某二级倒立摆系统模型各参数代入式1-8，得出系数矩阵设, 写出Matlab程序如下：
A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1; 0,-2.57163,0.164291,-16.6674,0.0124145,0.005; 0,29.9499,-15.1957,40.3167,-0.204856,0.17380; 0,29.9499,65.4455,-49.3949,0.463474,-0.59148]; B=[0;0;0;8.64636;-20.9146;25.9146]; C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];D=[0;0;0]; %求开环特征值 r1=eig(A) %加入最优反馈器 q1=100;q2=10;q3=5000;q4=0;q5=0;q6=0; Q=[q1 0 0 0 0 0;0 q2 0 0 0 0;0 0 q3 0 0 0;0 0 0 q4 0 0;0 0 0 0 q5 0;0 0 0 0 0 q6];R=1; %求最优增益矩阵、黎卡提方程的解、闭环特征值 [K,P,r2]=lqr(A,B,Q,R) Ac=[(A-B*K)];Bc=[B];Cc=[C];Dc=[D]; T=0:0.02:20;U=zeros(size(T)); x0=[0;-0.05;0.1;0;0;0]; [Y,X]=lsim(Ac,Bc,Cc,Dc,U,T,x0); %绘制下摆偏离垂直方向的角度变化曲线 figure(1);plot(T,Y(:,1)); xlabel('Time/sec');ylabel('01/rad');grid; %绘制上下摆角度之差的曲线 figure(2);plot(T,Y(:,2)); xlabel('Time/sec');ylabel('02-01/rad');grid; %绘制小车位移曲线 figure(3);plot(T,Y(:,3)) xlabel('Time/sec');ylabel('x(小车)/m');grid;

倒立摆实验报告

实验报告姓名：王琳学号：12030078一、控制对象描述本实验的控制对象是二级倒立摆系统，它主要由机电装置和控制装置两部分组成，机电装置的结构主要由小车、两根摆杆及连接轴构成。

假设系统中的每一根摆杆都是匀质刚体，忽略实验中的摩擦力，驱动力与放大器的输入成正比且无延迟地直接作用于小车上。

设定摆杆竖直向上时，下摆杆角位移、上摆杆角位移均为零，摆杆顺时针旋转为正。

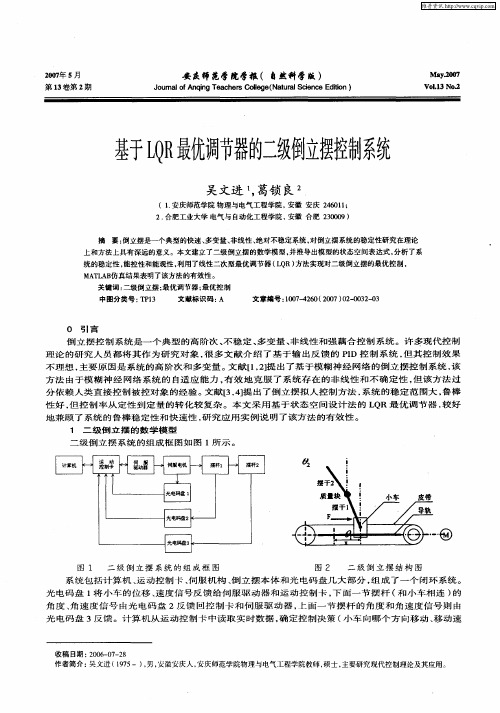
下图为二级倒立摆模型。

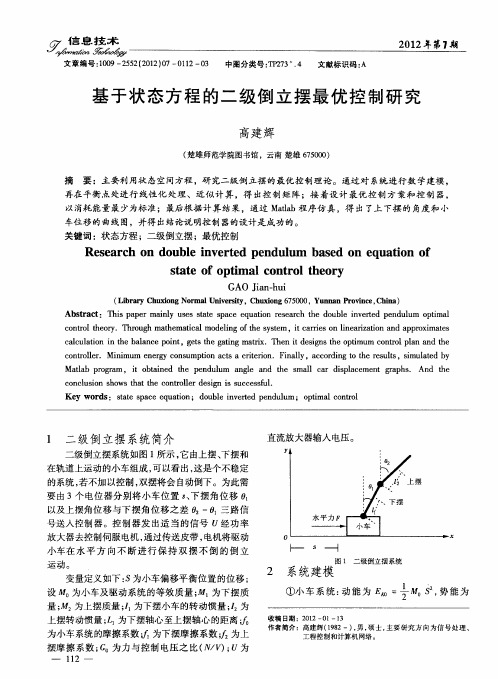
二、系统建模设x为小车质量，下摆杆质量为M1l1，上摆杆质量为M2，转动惯量为J1，上摆杆重心到转轴b 间的长度l2，小车与地面摩擦力系数f ，下摆杆转轴a 与b 间的长度L ，重力加速度g 。

运用牛顿力学定律建立方程：2212112211222222()()cos ()sin cos sin F f x m M M x M l M l M l M l M l M l ααααββββ∙∙∙∙∙∙∙=+++++-++-222222222222222222222222222sin cos sin sin sin 2sin cos sin cos sin cos cos cos cos J M gl M Ll M Ll M l M l M l x M Ll M Ll M l ββαβααβαββββββαβααβαββ∙∙∙∙∙∙∙∙∙∙=+∙+∙+∙+∙-+∙-∙-∙222221111122222222221111222222222sin sin sin 2sin sin sin sin cos sin sin cos cos cos cos cos sin cos cos J M gl M l M gL M L M L M Ll M Ll M l x M l M L x M L M Ll M Ll ααααααβααααββαββαααααααββαββ∙∙∙∙∙∙∙∙∙∙∙∙∙∙=+∙++∙+∙+∙+∙--∙-∙-∙+∙-∙经过线性化得到如下式子：12112222()()F f x m M M x M l M l M l αβ∙∙∙∙∙∙∙=++++++ 2222222222J M gl M l x M Ll M l ββαβ∙∙∙∙∙∙=---22111211211222()()()J M gl M gL M l M L x M l M L M Ll αααβ∙∙=+-+-+-参数取值：g=9.8；m=1.328；M1=0.22；M2=0.187；l1=0.303；l2=0.2261122334455660100000016.7 1.300.100.70001000039.118.107.90 1.70000010068.514.4025.900.3x x x x x x F x x x x x x ∙∙∙∙∙∙⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦ 123456100000001000000010000000100000001000000010x x x x x Y F x x x ααββ∙∙∙⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦可以得到A 、B 、C 、D ：10000016.7 1.300.10000100039.118.107.90000001068.514.425.90A ⎡⎤⎢⎥--⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥⎢⎥--⎣⎦00.701.700.3B ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦100000010000001000000100000010000001C ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦000000D ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦三、系统分析与控制器设计采用线性二次型最优控制器(linearquadraticregulator —LQR)对系统进行控制。

基于LQR最优调节器的二级倒立摆控制系统

分依赖人类直接控制被控对象的经验。文献【，］出了倒立摆拟人控制方法，统的稳定范围大，棒３４提系鲁性好，控制率从定性到定量的转化较复杂。本文采用基于状态空间设计法的Ｌ但ＱＲ最优调节器，好较地兼顾了系统的鲁棒稳定性和快速性，究应用实例说明了该方法的有效性。研
维普资讯
２ｏ年５月Ｏ７
安度师范学院学报（自熊科学版）
ＪｕｌｆｎｉｅｃｅｓＣｌｇ（ａｒｃｎｅＥｉｎｏｍａｏＡｑｇＴａｈｒｏｅｅＮｔａＳｉｃｄｉ）ｎｌｕｌｅｔｏ
收稿日期：０６０ — ８２０ — ７２
作者简介：吴文进（９５，，１７一）男安徽安庆人，安庆师范学院物理与电气工程学院教师，硕士，主要研究现代控制理论及其应用。
维普资讯
锁良：基于ＬＲ最优调节器的二级倒立摆控制系统Ｑ得
摘要：倒立摆是一个典型的快速、多变量、非线性、绝对不稳定系统。对倒立摆系统的稳定性研究在理论
上和方法上具有深远的意义。本文建立了二级倒立摆的数学模型。并推导出模型的状态空间表达式，分析了系
统的稳定性，能控性和能观性。利用了线性二次型最优调节器（ＱＲ）Ｌ方法实现对二级倒立摆的最优控制，ＭＡＬＢＴＡ仿真结果表明了该方法的有效性。关键词：二级倒立摆；最优调节器；最优控制

基于LQR二级倒立摆控制系统研究论文

基于LQR的二级倒立摆控制系统研究摘要倒立摆系统是一个典型的多变量、非线性、强耦合和快速运动的高阶不稳定系统，它是检验各种新的控制理论和方法有效性的典型理想模型。

在其控制过程中，能有效地反映诸如镇定性、鲁棒性、随动性以及跟踪等许多关键问题。

本文主要研究二级倒立摆LQR控制方法。

首先建立了二级倒立摆的数学模型，然后对二级倒立摆的数学模型进行控制设计，应用遗传算法确定系统性能指标函数中的加权阵Q，R得到系统状态反馈控制矩阵。

最后，用MATLAB进行了系统仿真。

在几次凑试Q矩阵值后系统的响应结果都不尽如人意，于是采用遗传算法对Q矩阵优化。

仿真结果证明：经过遗传算法优系统响应能更加满足设计要求。

关键词二级倒立摆；LQR控制；遗传算法Research on double inverted pendulum controlsystem based on LQRAbstractThe inverted pendulum is a typical high order system, with multi- variable, non-linear, strong-coupling, fleet and absolutely instable. It is representative as an ideal model to prove new control theory and techniques. During the control process, pendulum can effectively reflect many key problems such as equanimity, robust, follow-up and track, therefore.This paper studies a control method of double inverted pendulum LQR. First of all, the mathematical model of the double inverted pendulum is established, then make a control design to double inverted pendulum on the mathematical model, and determine the system performance index weight matrix Q, R by using genetic algorithm in order to attain the system state feedback control matrix. Finally, the simulation of the system is made by MATLAB. After several test matrix Q value the results are not satisfactory response, then we optimize Q matrix by using Genetic Algorithm. Simulation results show: The system response can meet the design requirements effectively after Genetic Algorithm optimization.Key words Double inverted pendulum; LQR control; Genetic Algorithm.目录摘要 (I)Abstract (II)第1章绪论 (1)1.1引言 (1)1.2倒立摆设备简介 ..................................... 错误!未定义书签。

基于状态方程的二级倒立摆最优控制研究

运动。
０
卜一Ｓ — ＿ — —１
图１二级倒立摆系统
变量定义如下：．ｓ为小车偏移平衡位置的位移；设为小车及驱动系统的等效质量；为下摆质Ｍ。
量；为上摆质量；为下摆小车的转动惯量；２，１为
车位移的曲线图，并得出结论说明控制器的设计是成功的。
关键词：状态方程；二级倒立摆；最优控制
Ｒｅｅｒｈｏｏｂｅｉｖｒｅｅｄｌｎａｅｎｅｕｔｏｆｓａｃｎｄｕｌｎｅｔｄｐｎｕｕｌｂｓｄｏｑａｉｎｏｓａｅｏｐｉａｏｔｏｈｏｙｔｔｆｏｔｍｌｃｎｒｌｔｅｒ
Ｋｅｒｓｓｔｐｃｑａｉｎ；ｄｕｌｎｅｅｅｄｌｍ；ｏｔｌｃｎｏｙｗｏｄ：ｔｅｓａｅｅｕｔａｏｏｂｅｉｖｒｄｐｎｕｕｔｐｉｏｔｌｍａｒ
１二级倒立摆系统简介
二级倒立摆系统如图１所示，介：高建辉（９２一）男，士，１８，硕主要研究方向为信号处理、工程控制和计算机网络。
摘
要：主要利用状态空间方程，研究二级倒立摆的最优控制理论。通过对系统进行数学建模，
再在平衡点处进行线性化处理、近似计算，得出控制矩阵；接着设计最优控制方案和控制器，以消耗能量最少为标准；最后根据计算结果，通过Ｍａａ序仿真，得出了上下摆的角度和小ｌｆｂ程

基于倒立摆的两种控制策略的研究

基于倒立摆的两种控制策略的研究作者：潘健王俊汤才刚来源：《现代电子技术》2008年第01期摘要：倒立摆系统被广泛应用于检验各种控制理论和控制策略的有效性中。

分析了两种简单而有效的控制策略：极点配置法和线性二次最优控制策略的LQR法，并通过Matlab仿真对单极倒立摆系统进行了控制效果的对比，从理论和仿真结果上讨论了这两种控制策略的优缺点。

关键词：倒立摆;极点配置法中图分类号：TP273 文献标识码：A文章编号：Study of the Two Control Strategies Based on the Inverted Pendulum(School of Electrical & Electronic Engineering,Hubei University ofTechnology,Wuhan,430068,China)Abstract：Inverted pendulums are widely used to verify some qualities and effect of certain control theory or method.The paper analyses the two single and effective control strategies:the pole-placement method and the optimization strategies of LQR method.We compare the control results of the single inverted pendulum system with the two control strategies by the Matlab experiment.The paper points out the advantage and disadvantage between the two different methods through theories and the results of the Matlab experiment.Keywords：inverted pendulum;pole-placement method;LQR;Matlab1 引言倒立摆系统是一种绝对不稳定、高阶次、多变量、强耦合的非线性系统，是控制理论研究中理想的实验对象，他为控制理论的教学、实验和科研构建了一个良好的实验平台，促进了控制新理论和新思想的发展。

平面二级倒立摆的线性二次最优控制

林健．面向 “ 卓越工程师 ” 培养的课程体系和教学内容改革
［８］李
正，林
凤．美国高等工程教育改革探析［Ｊ］．高等工程教育
研究，２００８（２）：３１－３５．
［９］马必学，刘晓欢．理论与实践一体化教学模式的改革创新［Ｊ］．教
ｍ
Ｔ
ｈ
ｅ
［６］段学超，仇原赢，盛英．平面二级倒立摆的圆周行走与镇定控
制ｆＪ］．自动化学报，２００７，３３（１２）：１３３７ — １３４０．
＾．
［７］ＣｒａｉｇＪＪ．Ｉｎｔｒｏｄｕｃｔｉｏｎｔｏｒｏｂｏｔｉｃｓ：ｍｅｃｈａｎｉｃｓａｎｄｃｏｎｔｒｏｌ［Ｍ］．３ｔｈ
［１１］唐志平．供配电技术［Ｍ］．北京：电子工业版社，２００９．
［１２］张巍山．电］＿基础［Ｍ］．北京：中国电力｝｝＿｛版社，２０１０．［１３］史宜巧，孙业明，景绍学．ＰＬＣ技术及应用 —— 项目教程［Ｍ］
［１５］刘志峰．丁控组态软件实例教程［Ｍ］．北京：电子Ｔ业出版社，
２００８．
ｍ
Ｕ
＂
［１６］仲景冰工程项目管理ｐ［Ｍ］．武汉：华中科技大学出版利：，２００９．

倒立摆研究报告(DOC)

基于LQR控制的二级倒立摆系统研究作者：牛娟031210308王晨琳031210307王鹤彬031210312 学院：自动化指导老师：王晶、陆宁云摘要倒立摆系统是一种高阶次、不稳定、多变量、非线性、强耦合的系统，是进行控制理论研究的典型实验平台。

本文采用最优控制的方法设计二级倒立摆系统的控制器。

首先简要介绍了倒立摆以及倒立摆的几种常见控制方法，着重介绍了最优控制理论，其次对二级倒立摆系统进行了数学建模，最后对线性二次型最优控制原理进行了分析并使用MATLAB进行了仿真。

关键词：二级倒立摆，最优控制目录一、绪论 (3)1.1、倒立摆系统简介 (3)1.2、倒立摆系统的控制算法 (3)1.3、小结 (4)二、直线倒立摆的建模 (4)2.1、直线二级倒立摆的建模 (4)2.2、直线二级倒立摆的定性分析 (6)三、基于MATLAB的LQR仿真 (9)3.1、最优控制（LQR）简介 (9)3.2、线性二次型最有调节器原理 (9)3.3、MATLAB仿真 (10)3.4、SIMULINK仿真 (11)四、结束语 (13)4.1、小结 (13)4.2、未解决问题展望 (13)五、附录 (13)一、绪论1.1、倒立摆系统简介倒立摆系统是一种高阶次、不稳定、多变量、非线性、强耦合的系统，是进行控制理论研究的典型实验平台。

许多抽象的控制理论概念如系统稳定性、可控性和系统抗干扰能力等等，都可以通过倒立摆系统实验直观的表现出来。

在控制理论发展的过程中，某种控制理论的正确性及可行性需要通过设计一个控制器去控制一个典型的控制对象去加以验证。

倒立摆系统正是这样一种比较典型的控制对象。

最简单的倒立摆可由一个可在水平轨道上自由移动的小车和倒置摆铰链组成。

倒立摆的种类繁多，分类方法也多种多样：按结构来分有直线倒立摆，环形倒立摆，平面倒立摆；按级数来分有一级摆，二级摆，三级摆乃至更高级摆；按运动轨道来分有水平轨道倒立摆，倾斜轨道倒立摆；按控制电机数目来分有单电机倒立摆，多电机倒立摆。

线性二次型最优控制在倒立摆系统中的应用

中图分类号：Ｄ５Ｔ８７
ＡｐｃｔｎｏＱＲｎｅｔｄＰｎｕｕＳｓｍｐｆａｉｆｉｏＬｉＩｖｒｅｅｄｌｍｙｔｎｅ
ＸＩｉｒｎＵｅＥＬ —ｏｇ．Ｗｉ
（ｏｅｅｏＥｅｔｃｌｎｉｅｎ，ｉｉｇＵｉｒｔ，ｒｍｉ３０８ｈａＣｌｇｌｒａＥｓｅｒｇＸｎａｎｅｉＵｕｑ８００，Ｃｉ）ｌｆｃｉｎｉｊｎｖｓｙｎ
有非常重要的位置．由于线性二次型（Ｑ性能指标Ｌ）
态特性等优点，性二次型在控制界得到普遍重线
视．通过倒立摆ＬＲ最优控制系统设计与研究，Ｑ并从实时控制效果出发，找出系统的动态响应与加权
阵Ｑ和之间的变化规律，用于指导实践．并
收稿日期；０８６１２０ —０ —１基金项目：新疆维吾尔自治区精品课程建设项目（０５３；２０４）新疆大学院校联合项目（７２１．０００）作者简介：谢丽蓉（９９，，１６一）女讲师，主要从事自动控制理论、系统教学与研究．
ｉｅｅｎｕｔｇｏｅｔＴｅｅｈｅａｉＱａｄＲａ￣ｚｒｇｍｅｎｅｅｎｎｒｄｐｄｕｖｔｅｌｍｈｏｄｅｃ．ｈｉｔｍｔｘｒａｙｅｔｏｈｓｖｒｐ — ｆｗｇｄｒｎｅｎｄｈｕｏｉｔｅｄｄｕｘｅｉｎｅｒｉｅｅＱａｄＲ．ｅｂｓｗａｅｂｅｕｄｏｔｅｅｎｔｓｍ — ｌｕｅｐｒｔｔｄｔｍｎＴａｉｌｓｖｅｎｆｎｕｂｔｅｅｓｔｒｍｍｅｓｏｅｈｔｎｈｃａｈｏｗｈｙｅｅｓｎｅｐｒｒａｃｄｔｅｍｔｘＱａｄＲ．Ｔｅｅｐｒｅｔｅｕｓｓｏｅｃｎｌｉｉｔａｄｅｐｓｆｍｎｅａａｈｘｅｍｎｌｒｌｈｗｔｏｃｓｎｉｒｅｏｎｈｉｒｎｉａｓｔｈｕｏｓｇｎｈ

基于参数优选法LQG最优控制的倒立摆控制

基于参数优选法LQG最优控制的倒立摆控制
刘方霆;刘危
【期刊名称】《工业控制计算机》
【年(卷),期】2013(026)009
【摘要】为了实现对单级倒立摆系统的控制,提出了一种基于LQG(线性二次型高斯控制)的倒立摆系统控制方法.利用LQR(线性二次最优)构建系态反馈矩阵,再结合Kalman滤波器,综合得到了LQG控制器,并对该控制器的参数进行了优化设计.通过MATLAB仿真,验证了采用的控制算法能够有效地对单级倒立摆系统进行控制,系统超调量较小,并具有一定的鲁棒性.
【总页数】3页(P55-57)
【作者】刘方霆;刘危
【作者单位】空军预警学院研究生管理大队,湖北武汉430019;空军预警学院五系,湖北武汉430019
【正文语种】中文
【相关文献】
1.二级倒立摆的 LQG 最优控制研究 [J], 苏航
2.三级倒立摆的LQG最优控制应用研究 [J], 叶建斌;郭鸿武
3.基于线性二次型最优控制器的平行双倒立摆系统稳定控制 [J], 戚东东;张春;张传松;谭子良
4.基于SimMechanics的单级倒立摆最优控制算法研究 [J], 方鹏;王旭;匡毅
5.基于嵌入式控制器的直线倒立摆最优控制研究 [J], 刘翔;王中杰
因版权原因，仅展示原文概要，查看原文内容请购买。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A 21 = T0 M G
FT0 , B 2 =
- 1
r
・
r
M (0 , 0)
θ 1 θ 2
r
= F (0 , 0 , 0 , 0)
θ 1 + θ 2
・
・
对连续系统 ( 3) 进行离散化处理 , 可得离散化后的系统的状态方程为 X k + 1 = GX k + HU k ( 4) Yk = CX k
( 2)
T A ( Ts 其中 G = e A TS , H = ∫ 0 Se 期 , 实验中取 Ts = 0102s t)
B d t , Ts — — — 采样周
1 + GU N (0 , 0) Ξ θ
θ 2 其中
M ( 0 , 0)
2 控制器的设计 [3 - 5 ]
=
M2 L 1 + M 1 l 1 J1 +
2 M1 l 1
本文中所设计的两种控制器都需要用到系统状态的
M2 l2 M2 L 1 l2 J 2 + M2 l2 2
M0 + M 1 + M 2 M2 L 1 + M 1 l 1 M2 l 2 1 l 2
- F0
F ( 0 , 0 , 0 , 0)
0 F2 ( F1 + F2 )
r
・
r
M (θ 1, θ 2)
θ 1 θ 2
= F (θ 1, θ 2, θ 1, θ 2)
・
・
θ 1 θ 2
・・
+ N (θ 1, θ 2)
Ξ
r
θ 1 + GU θ 2
(1)
其中线性控制方法离不开被控系统的线性模型 , 为了进行线性控制器的设计 , 首先需要对被控系统进行建模。
收稿日期 :2004 - 02 - 23 ;修回日期 :2004 - 03 - 15 。作者简介 : 张义明 (1978 - ) , 男 , 安徽省枞阳县人 , 硕士 , 主要从事最优控制及制导、导航与控制 ( G NC) 一体化等方向的理论与工程研究。战兴群 (1970 - ) ,男 ,博士 , 副教授 , 主要从事电液伺服系统、工业控制、导航自动化及制导、导航与控制 ( G NC) 一体化等方向的理论与工程研究。图1 二级倒立摆系统的微机控制原理框图
0 引言
倒立摆系统是一个典型的高阶次、多变量、严重不稳定和强耦合的非线性系统。由于倒立摆的行为与火箭飞行以及两足机器人行走有很大的相似性 , 因而对其研究具有重大的理论和实践意义。由于倒立摆系统本身所具有的上述特点 , 使它成为人们深入学习、研究和证实各种控制理论有效性的实验系统。本文针对二级倒立摆系统的平衡控制问题 , 设计了两种控制方法 — — — 线性二次状态控制器 (LQR) 和线性二次输出控制器 (LQY) , 同时根据建模所得的二级倒立摆系统进行了仿真控制 ; 对所获得的控制结果进行了对比研究 , 不仅从理论上分析了两种方法各自的优缺点 , 而且从自不稳定的倒立摆实际控制系统中进一步证实了各方法的控制效果。
0
F2 ,
= 0 0 0
全反馈 , 而实际系统中直接可测的状态只有小车位置和倒立摆的位置。一种方法是通过采用状态观测器来得到小车以及倒立摆的速度 , 实际上对于倒立摆系统而言 , 虽然不能直接测量小车以及倒立摆的速度 , 但是可以很容易地通过对直接可测的小车位置和倒立摆位置的线性差分得到。这样 , 在进行状态反馈控制时 , 就不需要再设计状态观测器了。 211 线性二次状态控制器 (LQR) 设状态反馈调节律的形式为 U ( k ) = - KrX ( k ) ,
・
・
・
θ M2 l 2cos 2
F (θ 1, θ 2, θ 1, θ 2)
・・
M2 L 1 l 2cos (θ 2- θ 1)
=
・
- F0 0 0
( M1 l 1 + M2 L 1) sinθ θ 1・ 1
θ M2 l 2sinθ 2・ 2
为
・
-
( F1 + F2)
・
θ θ M2 L 1 l 2sin (θ 22 1) ・ 2 + F2
=
0 0
, B=
03 ×3
B2
, C = [ I3 × 3 03 × 3],
0
1
T0 = 0
0 1 - 1
- 1
0 0 1
N T0 , A 22 = T0 M
- 1 - 1
0 0
, 其中各参量的意义及参数值如表 1 所示。
・・
0
T0 M
- 1
在平衡点 θ 1 =θ 2 = 0 和θ 1 =θ 2 = 0 附近 , 对方程 ( 1) 进行线性化处理 , 亦即设 : sinθ ≈θ, cosθ ≈1 , 得
Study on Quadratic Optimal Control of a Double Inverted Pendulum
Zhang Yiming , Zhan Xingqun
(Dept. of Information Measurement Technology and Instruments , Shanghai Jiaotong Univ. , Shanghai 200030 , China) Abstract : Inverted pendulum system is difficult to control because of its instability. It becomes the wonderful experiment device to verify how about the control strategy in automatic control experiment. The double inverted pendulum is modeled and the controller is designed by us 2 ing quadratic optimal control theory to its equilibrium control question. The simulating results show that quadratic optimal control has the ability to control the representative nonlinear instability system. Key words : double inverted pendulum ; controller ; quadratic optimal control
置轨迹和倒立摆上、下摆角度轨迹以及控制输出曲线如图 2 中虚线所示。从仿真曲线可以看出 , LQY 控制器对自不稳定倒立摆系统的控制也是很有效的。
3 结论
引起的性能度量的相对重要性进行加权。在系统的仿真控制过程中 , 我们取 Q r = 116 ×I6 ×6 , R r = 018 。根据式 ( 6) 和式 ( 7) , 设计出状态反馈矩阵为 Kr = [ 01024 5 01373 7 11331 2 - 01001 8 01185 8 01194 1 ] 。对二级倒立摆系统进行状态反馈控制 , 取初值 X0 = [ 0 15/ 180 3 π 10/ 180 3 π 0 0 0 ] T , 仿真控制可得小车位置轨迹和倒立摆上、下摆角度轨迹以及控制输出曲线如图 2 中实线所示。从仿真曲线可以看出 , LQR 控制器对自不稳定倒立摆系统的控制是很有效的。其中 : 实线表示 LQR 控制时的情况 , 虚线表示 LQY 控制时的情况。 212 线性二次输出控制器 ( L QY) 设输出反馈调节律的形式为 U ( k ) = - Ky X ( k ) , 此时可通过使性能指标函数
∞
+ U ( k ) TR rU ( k ) ] ( 5)
级倒立摆系统进行状态反馈控制 , 取初值 X0 = [ 0 15/
180 3 π 10/ 180 3 π 0 0 0 ] T , 仿真控制可得小车位
( 6) 为最小 , 可求得 Kr = ( HTSH + R r) - 1 ( HTSG) 其中 S 由下列 Ricatti 方程获得 T T T - 1 T ( 7) G SG - G SH ( H SH + R r) H SG + Q r = S Q r , R r 分别用来对状态向量 X ( k ) 、控制向量 U ( k )
T θ θ X = [ x1 x 2 x 3 x 4 x5 x6 ] = [ r 1 2 - θ 1 r T θ θ 1 2 - θ 1] T θ 则 Y = [ x1 x2 x3 ] T = [ r 1θ 2 - θ 1] 那么根据式 ( 2) 并作适当变换得系统的状态方程
・・
意义小车及驱动系统的等效质量 (kg) 下摆质量 (kg) 上摆质量 (kg) 下摆转动惯量 (kg・ m2) (kg 上摆转动惯量・ m2) 下摆质心至轴心的距离 (m) 上摆质心至轴心的距离 (m) 下摆轴心至上摆轴心的距离 (m) 小车系统的摩擦系数 (N・ m・ s) 下摆摩擦阻力系数 (N・ m・ s) 上摆摩擦阻力系数 (N・ m・ s) 力与控制电压之比 (N/ V)
工业控制
计算机测量与控制 . 2004 . 12 ( 11 ) Computer Measurement & Control
・1067 ・
文章编号 :1671 - 4598 (2004) 11 - 1067 - 03 中图分类号 :TP273 文献标识码 :A
二级倒立摆的二次型最优控制研究
1 系统建模
为此 , 对二级倒立摆系统作如下假设 [1 ] : ( 1) 上下摆杆在运动中是不变形的刚体 ; ( 2) 齿型带与带轮之间无相对滑动 , 齿型带无拉长现象 ; ( 3) 放大器的输出与输入呈严格的线性关系 ; ( 4) 小车在运动过程中所受的摩擦阻力矩正比于小车速度 , 摆转动时所受摩擦阻力矩正比于摆转动角速度。二级倒立摆系统的微机控制原理框图 [2 ] 如图 1 所示。根据动力学理论 , 二级倒立摆的动力学方程如下 :