负命题推理规则分析问题实例

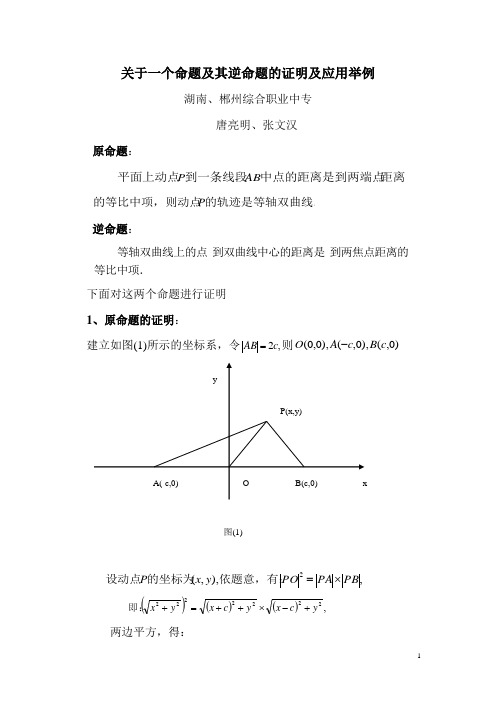
关于一个命题及其逆命题的证明及应用举例湖南、郴州综合职业中专唐亮明、张文汉原命题：距离中点的距离是到两端点到一条线段平面上动点AB P的轨迹是等轴双曲线．的等比中项，则动点P逆命题：等比中项．到两焦点距离的到双曲线中心的距离是 等轴双曲线上的点 下面对这两个命题进行证明1、原命题的证明：建立如图(1)所示的坐标系，令,2c AB =则)0,(),0,(),0,0(c B c A O -,),,(2PB PA PO y x P ⨯=依题意，有：的坐标为设动点()()(),2222222y c x y c x y x +-⨯++=+即：两边平方，得：()()()()[],4222222222y y c x c x c x y x +-+++-=+,22224222242244224y y c y x c x c x y y x x ++++-=++整理，得：,02242222=+-c x c y c2222c y x =-∴………………① ∵方程①表示的等轴双曲线，22cb a ==∴方程①可写成为 222a y x =-…………②2、逆命题的证明，可有以下两种常用证法：证法一：如图⑵所示，等轴双曲线的)0(,222>=-a a y x ).0,()0,(21c F c F 、焦点-∵()()222221y c x y c x PF PF +-⨯++=⨯422224224222y y c y x c x c x ++++-= ()()42222222c y x c y x +--+=，即又由2,222222222c y x c a a y x =-=⇒=- ∴21PF PF ⨯()42222222c c c y x +⨯-+=22y x +=2PO =.∴逆命题得证．证法二：。

原命题是真命题,逆命题是假命题的例子以下是 9 条符合要求的内容：
1. 咱就说“对顶角相等”，这原命题绝对是真命题吧，但它的逆命题“相等的角是对顶角”，那可纯粹是瞎扯呀！就好比你说两个长得一样高的人一定是双胞胎，这能对嘛！
示例：你看那个角，它们是对顶角，肯定相等；但相等的角可不一定是对顶角呀，别搞混咯！
2. 还有“如果一个数能被 2 整除，那么它是偶数”，原命题没问题吧，但逆命题“偶数一定能被 2 整除”，哎呀，这不是废话嘛！我就不信你还能找出个偶数不能被 2 整除的？
示例：这个数能被 2 整除，哇，那它肯定是偶数呀；但偶数一定是因为能被
2 整除才是偶数呀，多明显！
3. “菱形的对角线互相垂直”，这确实是真命题吧，但“对角线互相垂直的四边形是菱形”，这不是在开玩笑嘛！就像说会飞的动物一定是鸟一样，离谱呀！
示例：看那个菱形的对角线，垂直着呢；可那些对角线垂直的图形，不一定就是菱形呀，清醒点吧！
4. “同位角相等”，原命题是真呀，可“相等的角是同位角”，这不是乱套嘛！难道只要角相等就是同位角啦？那世界不就乱套啦！
示例：在这两条直线被第三条直线所截的情况下，同位角相等哦；但相等的角哪能都成同位角啦，真荒唐！
5. “直角三角形斜边上的中线等于斜边的一半”，这绝对对呀，但“等于斜边一半的线段就是斜边上的中线”，这不大错特错嘛！就好比说穿红衣服的一定是新娘一样，可笑不！
示例：这可是直角三角形，它斜边上的中线肯定等于斜边一半呀；但说等于斜边一半的线就是中线，可别闹了！
6. “等角的余角相等”，这肯定没错啦，但“余角相等的角是等角”，这不是理所当然的嘛，还。

矛盾命题和负命题
矛盾命题是指两个命题在逻辑上相互矛盾的情况，也就是说，它们中只有一个是真的，另一个一定是假的。

举个例子，命题A：“这
个苹果是红色的”，命题B：“这个苹果不是红色的”。

如果A是真的，那么B就是假的；如果B是真的，那么A就是假的。

因此，这两个命题构成矛盾命题。

而负命题则是对某一命题的否定。

以上述例子为例，如果A是“这个苹果是红色的”，那么它的负命题就是“这个苹果不是红色的”。

负命题在逻辑上等价于矛盾命题的非真即假的结构。

在逻辑推理中，矛盾命题和负命题经常被用来进行证明和反证法。

同时，理解矛盾命题和负命题也有助于我们在日常生活中更准确地表达和理解事实、观点，避免逻辑上的混淆和误解。

- 1 -。

第三节负判断等值推理一、负判断等值推理的含义负判断等值推理是根据负判断的等值关系进行推演的推理。

表现为：通过否定某一判断而推出新的判断。

例如：(1) 不能既要马儿跑又要马儿不吃草，所以，或者马儿不能跑，或者马儿要吃草。

(2) 并非或是可迟到或是可早退，所以，既不可迟到，又不可早退。

(3) 并非如果努力就学得好，所以，努力也学不好。

这些都是负判断等值推理。

例(1)是否定联言判断的等值推理；例(2)是否定选言判断的等值推理；例(3)是否定假言判断的等值推理。

二、负判断的等值关系每一个负判断都有一个和它等值的判断。

所谓两个判断等值，就是说这两个判断的真假值相等，它们真则同真，假则同假。

1．简单判断负判断的等值推理﹁SAP＝SOP ﹁SEP＝SIP﹁SIP＝SEP ﹁SOP＝SAP2．复合判断负判断的等值推理(1) ﹁ (p∧q) 〓﹁p∨﹁q(2) ﹁ (p∨q) 〓﹁p∧﹁q(3) ﹁ (p q) 〓 (p∧q) ∨（﹁p∧﹁q）⑷﹁ (p→q) 〓 p∧﹁q⑸﹁ (p←q) 〓﹁p∧q⑹﹁(p←→)q)〓（p∧﹁q）∨（﹁p∧q）(7) ﹁（﹁p）〓 p三、注意问题在使用负判断等值推理方法时，应注意以下几个问题：第一，根据负判断的等值式，否定联言判断得出的是选言判断；否定选言判断得出的是联言判断。

但在日常生活中却容易在这里发生错误，往往由否定联言判断而推出联言判断，或由否定选言判断推出选言判断。

例如：由“不是你能去同时他也能去”推不出“你不能去同时他也不能去”，而只能推出“或是你不能去，或是他不能去”。

再如：由“并非或者你能去或者他能去”推不出“或者你不能去，或者他不能去”，而只能推出“你不能去，他也不能去”。

第二，复合判断的肢判断必须具有某种联系，否则，否定复合判断的等值推理就没有实际的意义。

如“并非2011年1月1日是星期一，并且火星有五个卫星”。

这个负判断的肢判断之间没有一定意义上的联系，所以它的等值推理的结论“或者2011年1月1日不是星期一，或者火星没有五个卫星”就没有实际意义。

负数的逻辑推理案例负数，在数学中是指小于零的数。

它们在我们日常生活和数学领域中都起着重要的作用。

然而，负数的逻辑推理是一种特殊的推理方式，其原理和应用需要我们深入探讨和理解。

本文将通过解析案例来探讨负数的逻辑推理，旨在帮助读者更好地理解负数的逻辑思维。

案例一：负数的加法推理故事背景：小明身上有一美元钱。

他在赌桌上赢了一半的钱，又再赢了一半的钱，最后又再赢了一半的钱。

请问小明手上还剩下多少钱？解析：首先，我们可以将小明身上的钱表示为“$1”。

根据故事，小明在赌桌上赢了一半的钱，即剩下的钱是原来的一半，可以表示为“1/2 * $1”。

然后，小明再次赢了一半的钱。

这意味着他剩下的钱是前一次剩下的钱的一半，即“(1/2 * 1/2) * $1”。

最后，小明又赢了一半的钱，同样道理，他手上剩下的钱是前一次剩下的钱的一半，即“(1/2 * 1/2 * 1/2) * $1”。

通过乘法运算，我们可以将上述推理过程简化为“(1/2)^3 * $1”。

根据乘法的规则，我们可以将“(1/2)^3”进一步计算为“1/8”。

因此，小明手上的钱可以表示为“1/8 * $1”或“$0.125”。

结论：根据逻辑推理，通过三次赌博，小明最终手上剩下的钱是0.125美元，即12.5美分。

案例二：负数在减法运算中的逻辑推理故事背景：在一个商店里，小红买了一个价值5美元的商品，却只给了收银员10美元的钞票。

请问，小红找回的零钱是多少？解析：首先，我们可以将小红实际需要支付的金额表示为“-$5”。

这是因为小红实际上欠了商店5美元。

其次，小红给了收银员10美元，所以我们可以将这部分表示为“$10”。

根据减法的规则，我们可以将二者相减，即“$10 - (-$5)”。

根据负数的性质，减去一个负数等于加上该负数的绝对值。

所以，“$10 - (-$5)”可以简化为“$10 + $5”。

通过加法运算，我们可以得出结论，小红找回的零钱是15美元。

结论：根据逻辑推理，小红找回的零钱是15美元。