第五章+微分方程---万有引力定律的发现

万有引力定律的发现历程在很早以前，人们就在不断地探索天体运动的奥妙．亚里士多德曾提到过力的概念，他认为力是产生非自然运动的原因，力的作用只有在相互接触时才能传递，因此，对于遥远的天体，这个力是毫无用处的．开普勒为天体运动奥妙的揭开做出了重大贡献,但却未解开天体运动的动力学之谜．1645 年法国天文学家布里阿德提出一个假设：从太阳发出的力，和离太阳距离的平方成反比．笛卡儿1644 年提出“旋涡"假说，把行星的运动归结为动力学原因．1666 年意大利的玻列利提出引力是距离的幂的某种函数．1673 年惠更斯在研究摆的运动时给出了向心加速度理论．英国的胡克已经觉察到引力和重力有同样的本质，1674 年他提出引力随离吸引中心距离而变化，1680 年他又进一步提出了引力反比于距离的平方的假设．哈雷的伦恩从圆形轨道与开普勒定律出发,导出了作用于行星的引力与它们到太阳的距离的平方成反比．当科学的接力棒传到了牛顿手中时,他便向万有引力定律的红线冲刺了．他站在前人的肩上，发挥他卓越的才能，建立了万有引力定律，为科学做出了重大的贡献．牛顿发现万有引力定律的过程中包含着丰富的物理学思想和物理学方法论内容，其主要的思路与运用的物理学方法大致体现在以下几方面．一、运用科学想象和推理，牛顿论证了行星运行都要受到一个力的作用牛顿对行星运动的研究工作首先是从研究月球开始的．牛顿想象，如果没有任何力作用于月球的话，根据牛顿当时已发现的牛顿第一定律可知，月球就应当做匀速直线运动．但月球是绕地球作圆周运动,所以月球必定要受到力的作用．牛顿当年写道：“没有这种力的作用月球不可能保持在自己的轨道上；如果这个力比轨道所需的力小,则它使月球偏离直线的程度不够;如果这个力比轨道所要求的力大,则它使月球偏离直线的程度太大，并使月球的轨道更靠近地球．”那么迫使月球绕地球旋转的力的性质是如何的呢？据说,有一次牛顿正在思考这个问题时，忽然看到一个苹果从树上掉了下来，他吃了一惊，同时便陷入了沉思．当时已知苹果是受重力作用而下落的,他推想,如果苹果树长得很高，熟透了的苹果会不会落地呢?当然是会的！但如果苹果树长得象月球那么高，树上的苹果是否还会落地呢,牛顿作了合理的设想，设想这种作用力的范围要比通常所想象的还要大得多，比如说，很可能一直延伸到月球那么高,因此，这样既使苹果树长得象月球那么高,苹果仍会落地的．正是这种作用力使地球对月球施加影响．同时，从开普勒第一定律（行星沿椭圆轨道绕太阳运行，太阳位于这些椭圆的一个焦点上）可知，各行星和卫星都是沿椭圆形路径运动（非匀速直线运动）因此，根据牛顿第一定律便可推知，各行星如卫星的运动都要受到一种力的作用．二、运用类比方法，牛顿推证了行星运行所受到的力是一种连续地指向一确定中心的作用力牛顿在由地面上的苹果下落联想到天上的月球也受一种力的作用,但进而思考,月球为什么不会象树上的苹果那样落地呢？这样他又联想到物体的旋转问题：绳子的一端系着一块石头，另一端抓在我们手中，让石头作旋转运动,这时如果我们松手，石头就会沿直线轨道飞出去，这说明石头之所以作圆周运动是由于一种力拉着石头．进而类比，这块石头好比月球，而我们的手又相当于地球，手通过绳子施于石头的力又很相似于地球施于月球的作用力．牛顿接着又描述了从高山上平抛一个铅球的理想实验，他设想,从高山上铅球平抛出去，本来应当笔直的前进,可是在重力作用下，它就沿抛物线落到了地面．如果平抛速度增加，它就会落得更远一些，再增加抛出速度,则铅球可能会绕地球半圈．当抛出速度足够大时,铅球就会绕地球一圈、两圈、乃至永远绕地球作圆周运动而不落回到地面上，这说明,只要有一个指向确定中心点的力,又具有足够的初速度,则物体就可作圆周运动．把月球类比于这个铅球，则可知，月球受一个指向确定中心点的力，所以才会作圆周运动．行星也应如此．牛顿进一步在开普勒第二定律的基础上改换问题的提法，开普勒第二定律是说：对于任何一个行星来说,它的矢径（行星到太阳的联线）在任何地点、在相等的时间内，沿轨道所扫过的面积相等．（这条定律也适用于月球绕地球的运行）牛顿则寻找在相等的时间间隔内物体若受一指向确定中心的力的作用,物体到中心联线扫过的面积存在什么规律?牛顿从数学上证明了（证明过程从略）在这种情况下，各面积之间存在相等的关系．牛顿接着又证明了这个命题的逆命题，即在任何一曲线上运动的物体，如果它到一确定点的连线在相等时间内扫过相等的面积，则物体受一指向该确定点的向心力．牛顿接着由开普勒第二定律所概括的现象推出行星或卫星受一连续的指向一确定中心的力，并且这个中心就在椭圆的一个焦点上．三、运用数学方法，牛顿推导出行星运行所受到的向心力遵从平方反比定律牛顿在由开普勒第二定律得到的存在一个连结指向一确定中心点的力作用于行星上的基础上，进一步去寻找物体在前人提出的椭圆轨道上运动时，所受的指向椭圆焦点的向心力的规律．牛顿利用了开普勒第一定律，用数学方法证明了(证明过程从略）沿所有圆锥曲线(或双曲线、抛物线、圆、椭圆等)在任何时刻的向心力必定与该物体到焦点的距离平方成反比，其数学形式为F ＝c/R 2即—-向心力定律 式中R 是从该物体中心到椭圆焦点的距离，c 为该物体的一个常数．牛顿由开普勒第三定律进一步推知向心力平方反比定律．其数学推导为：设某一行星的质量为m ，行星的运行轨道近似圆（由于行星椭圆轨道的偏心率很小，如地球为0．0167，因而其轨道可近似看作圆）根据开普勒第二定律，可将行星视为匀速圆周运动由牛顿第二定律．F ＝ma ＝m ·22224)2(TmR T R R m R v ππ== 式中m —行星质量，T —行星运行周期，R-圆周轨道半径．再由开普勒第二定律．T 2= kR 3 代入上式得224kR m F π= 令k24πμ= 得 2R m F μ= 式中μ是一个与行星无关而只与太阳的性质有关的量,称为太阳的高斯常数;m 为行星质量．由上式可知：引力与行星的质量成正比.牛顿通过研究引力使不同大小的物体同时落地和同磁力的类比，得出引力的大小与被吸引物体的质量成正比,从而把质量引进了万有引力定律．牛顿又进一步用实验作了验证：他用摆做了一系列实验，实验的结果以千分之一的准确度表明，对于各种不同的物质,万有引力与质量的比例始终是一个常数．牛顿又接着作了大胆的假设,行星受到的引力与太阳的质量有关,并用数学作了推证地球对一切物体包括太阳的引力应为2R M F μ'= μ′—地球的高斯常数，M —太阳的质量 太阳对地球的引力为2Rm F μ=，式中m —地球的质量,μ—太阳的高斯常数 根据牛顿第三定律有：F ＝F ′即2R M μ'2R m μ= G mM ='=μμ G 是一个与地球和太阳的性质都无关的恒量，所以引力的平方反比定律的数学形式为2RMm G F = 四、运用演绎推理方法，牛顿把引力的平方反比定律推广到一切物体，得出一切物体间均存在引力的结论牛顿得到平方反比定律之后,寻求进一步的原因：符合这个定律的力是什么性质的力?它是由什么决定的？牛顿首先由月球运行情况探讨了使月球保持轨道运行的力与重力之间的关系．由平方反比定律可知,月球受一指向地球的力的作用，它与月球到地心距离的平方成反比．通过数学计算和实验验证，牛顿得到了月球受的向心力就是重力的结论，这样牛顿就把地面落体运动的原因和月球运行的原因归于同一了．此后，牛顿运用牛顿第三定律推知,地球对月球也有引力，地球对太阳也有吸引力．牛顿由木星卫星和木星有吸引、土星与土星卫星有吸引,行星与太阳之间有吸引力等现象出发，认为这些和月地之间的现象系“同类现象，使月球不能出离轨道的力的原因可推至于一切行星”．这样，牛顿就把天体和其运行中心之间的力都归于引力．此后，他又由土星、木星会合点附近相互间的“运动失调”以及太阳使月球的“运动失调”现象，提出行星之间和恒星与卫星之间均有引力的作用，于是才提出了万有引力的假说．这样，牛顿由研究月球、地球，以至研究行星、恒星、卫星等推出了一切物体相互间均存在引力的结论．五、运用归纳概括方法，牛顿总结出了万有引力定律，完成了万有引力定律的发现工作牛顿对提出的万有引力假说进行了充分的论证，牛顿由原来得出的天体运行向心力平方反比定律，得出万有引力符合平方反比关系;由引力使不同大小物体同时落地，得出引力的大小和被吸引物体的质量成正比；又由牛顿第三定律，得出吸引物体和被吸引物体的区分是相对的，所以引力也和吸引物体的质量成正比，从而得出引力符合221R m m GF =．这样,牛顿就完成了万有引力的发现工作．牛顿发现的万有引力定律的内容为：宇宙间的任何物体之间都存在相互作用的吸引力，这种吸引力的大小与它们的质量的乘积成正比，与它们之间距离的平方成反比，作用力的方向是沿两物体的联线方向，即21221R m m G F = G 为引力恒量（引力常数）；m 1m 2 分别为两个相互吸引的物体的质量；R 12为物体m 2 与m 1 的质心间距离．六、运用科学观察和科学实验验证万有引力定律理论牛顿的万有引力定律是经过科学观察和科学实验的检验后才得到普遍承认的：1．关于地球形状的测定牛顿根据他的引力理论指出，地球不是正球体，而是两极方向稍扁的扁球体，后经过法国科学家的几次测量证明了牛顿的推论是正确的．牛顿这个足不出户的人正确地给出了地球的形状，这显示了牛顿理论的威力．2．地月验证由运动学公式可计算出月球的向心加速度R TR v a n 2224π== 已知R ＝3.84×108 米；T ＝2。

万有引力定律的发现自从人类开始思考宇宙的奥秘，万有引力定律的发现就成为了人们关注的焦点之一。

这个定律的发现不仅揭示了物质世界的秩序，也使人类对宇宙的认识更加深入。

本文将以人类的视角，讲述万有引力定律的发现及其对人类的影响。

在人类的认知历史中，牛顿是第一个提出并完整描述万有引力定律的科学家。

他在1666年至1667年间，当他在家乡的农舍里避免瘟疫时，思考着当时的科学问题。

通过观察苹果掉落的现象，他开始思考落下的苹果为什么会受到地球的吸引力。

从这个简单的观察开始，牛顿逐渐发展出了万有引力定律。

万有引力定律简洁而深刻地描述了物体之间的相互作用。

它指出，任何两个物体之间都存在一种相互吸引的力，这个力的大小与物体的质量成正比，与物体之间的距离的平方成反比。

换句话说，质量越大的物体之间的引力越大，物体之间的距离越近，引力也越大。

牛顿的发现对人类的影响是巨大的。

首先，它使人类对宇宙的运行秩序有了更深入的认识。

我们知道，地球围绕太阳运行，月球围绕地球运行，这些都是因为万有引力的作用。

万有引力定律让我们明白，所有物体都相互吸引，这种相互吸引使得宇宙中的星体能够保持相对稳定的运行轨道。

万有引力定律的发现也推动了人类对科学方法的发展。

牛顿通过观察现象，形成假设，进行实验证实了他的理论。

这种科学方法的应用不仅使得万有引力定律得以发现，也为后来的科学研究提供了范例。

科学家们开始用这种方法来探索自然界的规律，并逐渐揭示了更多的奥秘。

万有引力定律的应用也对人类的生活产生了实际的影响。

例如，它在航天领域的应用使得人类能够准确地计算出飞船的轨道，从而使得宇航员能够安全地进入太空。

在工程设计中，人们也需要考虑到引力的影响，以确保建筑物的稳定。

万有引力定律可以说是人类科技发展的基石之一。

总的来说，万有引力定律的发现是人类认知宇宙的一个重要里程碑。

它揭示了物体之间的相互作用，推动了科学方法的发展，对人类的生活产生了实际的影响。

通过牛顿的发现，我们更加深入地认识了宇宙的运行规律，也使得人类对宇宙的探索更加深入。

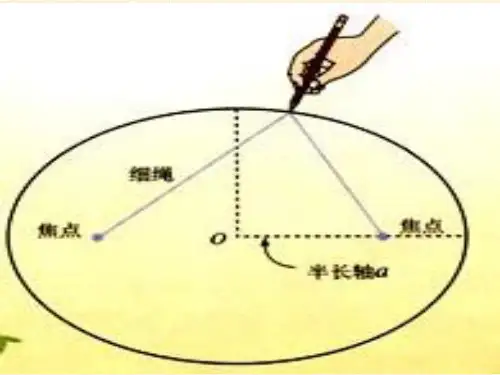
§5 万有引力定律的发现历史背景德国天文学家、数学家开普勒（1571—1630）在第谷.布拉赫对于行星运动大量观测资料的基础上，经过对观测数据长期深入的分析，归纳出著名的所谓行星运动三定律，即：（1）各颗行星分别在不同的椭圆轨道上绕太阳运行，太阳位于这些椭圆的一个焦点上；（2）每颗行星运行过程中单位时间内太阳—行星向径扫过的面积是常数；（3）各颗行星运行周期的平方与其椭圆轨道长半轴的3次方成正比。

由于当时尚没有计算变速运动的工具，而从开普勒定律可以看出行星运行速度是变化的。

十七、十八世纪许多科学家致力于行星沿椭圆轨道运行时受力状况的研究，终未得到有关引力的结果。

牛顿在研究变速运动过程中发明了微积分，又以此为工具在开普勒三定律和牛顿第二定律的基础上，成功地得到万有引力定律。

模型假设 对任一行星椭圆运行轨道建立极坐标系),(θr ,以太阳为坐标原点，长半轴方向为0=θ，向径r 表示行星的位置。

1、轨道方程为 )1(,,cos 12222e a b a b e r -==+=ρθρ（1） 其中b a ,为椭圆的长短半轴，e 为离心率。

2、单位时间内向径r 扫过的面积是常数A ，即A r =•θ221 （2） 3、行星运行周期T 满足32a T λ= （3）4、行星运行时受的作用力→f 等于行星加速度••r 和质量m 的乘积，即→••→=r m f （4） 模型建立 引入基向量 ⎪⎩⎪⎨⎧+-=+=→→θθθθθcos sin sin cos j i u j i u r （5） 向径→r 可表示为：→→=r u r r 。

以下记dt d ∆=∆• （6） 由（5）可得 ⎪⎩⎪⎨⎧-==→•→→•→••r r u u u u θθθθ （7） 由（6）、（7）两式可得→•→•→→→+=+=••θθu r u r u r u r r r r r （8）→••••→•••→•→••→••→•→••••⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛-=++++=••θθθθθθθθθθu r r u r r u r u r u r u r u r r r r r 22 （9） 根据（2）式得 22r A =•θ，34r r A •••-=θ （10） 于是 02=+••••θθr r ，（9）式化为 →•••••⎪⎪⎭⎫ ⎝⎛-=→r u r r r 2θ （11） 对（1）式求导，并利用（10）式•θ的结果，得()θρθθθρsin 2cos 1sin 2Ae e r =⋅+=•• （12） ()32224cos 4cos 2r r A r e A Ae r ρρθρθθρ-==⋅=••• （13） 把（10）、（13）代入（11）式得 →••-=→r u rA r 224ρ （14） 把（14）、（6）代入（4）式得 →→-=0224r r m A f ρ ,r r r →→=0 （15） 又由（2），行星运行一个周期T 向径扫过的面积为ab π，所以 ab TA π= （16）由（1）、（3）、（16）式容易算出 λπρ22=A （17） 把（17）代入（15）式有 →→-=0224r r m f λπ （18） 将λπ24写成kM （k 为万有引力常数，M 为太阳质量），于是 →→-=02r r Mm k f （19） 模型验证 由于32aT =λ，232244T a πλπ=，()米111049.1⨯=a ，（秒）¨1016.37⨯=T ，()2311/1071.6秒千克米⋅⨯=-k ，()千克＝301096.1⨯M ，可算得192321007.134⨯=T a π ，191015.13⨯=kM ，验证了 kM T a =2324π。

万有引力定律的发现万有引力定律现在大家公认是牛顿发现的，连小学生也知道牛顿在苹果树下休息，看见苹果落地而想到万有引力的故事。

但它的发现岂只是看见苹果落地这么简单？万有引力公式：这个公式与库仑定律有着惊人的相似之处。

G为万有引力常量，由英国物理学家卡文迪许首先在实验室测出其大小。

在牛顿的时代，一些科学家已经有了万事万物都有引力的想法。

而且牛顿和胡克（即发明了显微镜并用显微镜观察到细胞结构的罗伯特虎克）曾经为了万有引力的发现优先权发生过争论，有资料表明，万有引力概念由胡克最先提出，但由于胡克在数学方面的造诣远不如牛顿，不能解释行星的椭圆轨道，而牛顿不仅提出了万有引力和距离的平方成正比，而且圆满的解决了行星的椭圆轨道问题，万有引力的优先发现权自然归属牛顿。

正如牛顿所说他是站在巨人的肩膀上。

万有引力发现前的准备开普勒有着不可磨灭的贡献。

开普勒是德意志的天文学家，幼年患猩红热导致视力不好，后来有幸结识弟谷，一年后弟谷过世，把他一生的天文观测资料留给了开普勒。

在此基础上，开普勒经过20年的计算和整理于1609年发表了行星运动的第一、第二定律。

后来又经过十年又发表了行星运动的第三定律。

牛顿老年在回忆过去的时候有这样的话：同年（1666年）我开始把引力与月亮轨道联系起来并找出如何估计一个天体在球体内旋转时用来趋向球面的力的方法。

根据开普勒的行星周期与于他们的距离轨道中心的距离的二分之三次方成正比的规律，我得出使行星沿轨道旋转的力必然与他们离旋转中心的距离的平方成反比的结论。

从而把使月亮沿轨道旋转所需的力与地球表面的引力相比较发现它它们符合得很接近。

所有这些发生在1665年和1666年两个时疫年内，因为那时正是我创造发明的黄金时期，我对数学和哲学的思考比此后的任何时都候来的多。

此后惠更斯先生发表的关于离心力的思想，我猜想他在我之前就有了，最后在1676和1677之间的冬天我发现了一个命题：利用与距离成反比的离心力行星必然环绕力的中心沿椭圆轨道旋转，这中心在椭圆的下部，从这中心作出的半径所经过的面积与时间成正比……摘自《从落体到无线电波——经典物理学家和他们的发现》作者：当代美国著名物理学家诺贝尔奖获得者埃米里奥·赛格雷从上面的话可以知道，牛顿的平方反比律是由开普勒的行星运动定律得出的。