第五章 微分方程模型
- 格式:doc
- 大小:315.00 KB
- 文档页数:7




![微分方程模型[整理版]](https://uimg.taocdn.com/86cc9de9f605cc1755270722192e453610665b62.webp)
第5章 微分方程模型5.1 某人每天由饮食获取10467焦热量,其中5038焦用于新陈代谢,此外每公斤体重需支付69焦热量作为运动消耗,其余热量则转化为脂肪,已知以脂肪形式贮存的热量利用率为100%,每公斤脂肪含热量41868焦,问此人的体重如何随时间而变化?5.2 生活在阿拉斯加海滨的鲑鱼服从Malthus 增长模型)(003.0)(t p dtt dp = 其中t 以分钟计。
在0=t 时一群鲨鱼来到此水域定居,开始捕食鲑鱼。
鲨鱼捕杀鲑鱼的速率是)(001.02t p ,其中)(t p 是t 时刻鲑鱼总数。
此外,由于在它们周围出现意外情况,平均每分钟有0.002条鲑鱼离开此水域。
(1)考虑到两种因素,试修正Malthus 模型。
(2)假设在0=t 是存在100万条鲑鱼,试求鲑鱼总数)(t p ,并问∞→t 时会发生什么情况?5.3 根据罗瑟福的放射性衰变定律,放射性物质衰变的速度与现存的放射性物质的原子数成正比,比例系数成为衰变系数,试建立放射性物质衰变的数学模型。
若已知某放射性物质经时间21T 放射物质的原子下降至原来的一半(21T 称为该物质的半衰期)试决定其衰变系数。
5.4 用具有放射性的14C 测量古生物年代的原理是:宇宙线轰击大气层产生中子,中子与氮结合产生14C 。
植物吸收二氧化碳时吸收了14C ,动物食用植物从植物中得到14C 。
在活组织中14C 的吸收速率恰好与14C 的衰变速率平衡。
但一旦动植物死亡,它就停止吸收14C ,于是14C 的浓度随衰变而降低。
由于宇宙线轰击大气层的速度可视为常数,既动物刚死亡时14C 的衰变速率与现在取的活组织样本(刚死亡)的衰变速率是相同的。
若测得古生物标本现在14C 的衰变速率,由于14C 的衰变系数已知,即可决定古生物的死亡时间。
试建立用14C 测古生物年代的模型(14C 的半衰期为5568年)。
5.5 试用上题建立的数学模型,确定下述古迹的年代:(1)1950年从法国Lascaux 古洞中取出的碳测得放射性计数率为0.97计数(min ⋅g ),而活树木样本测得的计数为6.68计数(min ⋅g ),试确定该洞中绘画的年代;(2)1950年从某古巴比伦城市的屋梁中取得碳标本测得计数率为4.09计数(min ⋅g ),活数标本为6.68计数(min ⋅g ),试估计该建筑的年代。
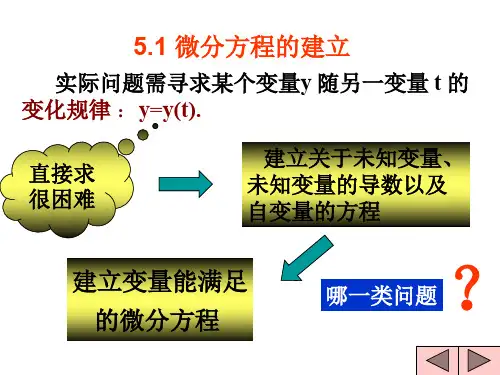




在解决实际问题时,弄清问题中的变量之间的函数关系或其变化趋势是至关重要的,而在一些较为复杂的变化过程中,变量之间的函数关系无法直接得到。
但是,在许多情况下,我们往往可以在理论或经验的基础上找到问题中的一些变量及其导数之间的关系。
也就是找出一个或几个含有未知函数及其导数所满足的方程,这个(些)方程就称为微分方程(组)。
然后通过求解微分方程(组)得到变量之间的函数关系,或者在微分方程(组)的基础上进行数值计算和渐进性态研究,从而了解整个系统的发展变化规律。
为了研究一些实际问题的变化规律,往往需要对所研究的问题进行适当的简化和假设,再建立数学模型,当问题中涉及变量的变化率时,就可以通过微分方程来建模。
微分方程模型主要是解决与导数,也即变化率相关的问题,但是;实际问题中一般并不会直接出现“导数”或“变化率”等词语,这时,就需要我们仔细分析,从中找出这些信息,一般来说,如果问题中涉及到“速率”、“增长”、“改变”、“变化”、“增加”、“减少”、“衰变”(在放射性问题中)、“扩散”、“边际的”(在经济学中)等问题时,往往就可以用微分方程(组)来建模。
微分方程模型的类型很多,在解决实际问题时,要根据具体情况选择不同的模型,建立模型时,应首先将实际问题概念化为文字方程,许多问题都遵循下面的模式:总讯宗勋净变化率=净增加率━净减少率如果变量之间的关系可以用这种形式来描述,我们就不难给出相应的微分方程(组)了。
在建立了微分方程模型之后,我们当然希望能得到微分方程的解,但是,对于大多数微分方程而言,要想直接求解往往是困难的,甚至是不可能的,此时我们可以通过对方程的定性分析得到有关的一些有用信息。
§1 确定性存贮模型为了使生产和销售有条不紊地进行,一般的工商企业总需要存贮一定数量的原料或商品,然而大量的库存不但积压了资金,而且会使仓库的保管费用增加。
因此,寻求合理的库存量乃是现代企业管理的一个重要课题。
需要注意的是,存贮问题的原型可以是真正的仓库存货,水库存水,也可以是计算机的存贮器的设计问题,甚至是大脑的存贮问题。
数学建模实验答案_微分⽅程模型实验07 微分⽅程模型(2学时)(第5章微分⽅程模型)1.(验证)传染病模型2(SI 模型)p136~138传染病模型2(SI 模型):0(1),(0)dik i i i i dt=-= 其中,i (t )是第t 天病⼈在总⼈数中所占的⽐例。
k 是每个病⼈每天有效接触的平均⼈数(⽇接触率)。
i 0是初始时刻(t =0)病⼈的⽐例。
1.1 画~dii dt曲线图p136~138取k =0.1,画出i dt di ~的曲线图,求i 为何值时dtdi达到最⼤值,并在曲线图上标注。
提⽰:fplot, fminbnd, plot, text, title, xlabel 1)画曲线图⽤fplot 函数,调⽤格式如下: fplot(fun,lims)fun 必须为⼀个M ⽂件的函数名或对变量x 的可执⾏字符串。
若lims取[xmin xmax],则x轴被限制在此区间上。
若lims取[xmin xmax ymin ymax],则y轴也被限制。
本题可⽤fplot('0.1*x*(1-x)',[0 1.1 0 0.03]);2)求最⼤值⽤求解边界约束条件下的⾮线性最⼩化函数fminbnd,调⽤格式如下:x=fminbnd('fun',x1,x2)fun必须为⼀个M⽂件的函数名或对变量x的可执⾏字符串。
返回⾃变量x在区间x1本题可⽤x=fminbnd('-0.1*x*(1-x)',0,1)y=0.1*x*(1-x)3)指⽰最⼤值坐标⽤线性绘图函数plot,调⽤格式如下:plot(x1,y1, '颜⾊线型数据点图标', x2,y2, '颜⾊线型数据点图标',…)本题可⽤hold on; %在上⾯的同⼀张图上画线(同坐标系)plot([0,x],[y,y],':',[x,x],[0,y],':');4)图形的标注使⽤⽂本标注函数text,调⽤格式如下:格式1text(x,y,⽂本标识内容, 'HorizontalAlignment', '字符串1')x,y给定标注⽂本在图中添加的位置。
第五章 微分方程模型、 某人每天由饮食获取10467焦热量,其中5038焦用于新陈代谢,此外每公斤体重需支付69焦热量作为运动消耗,其余热量则转化为脂肪,已知以脂肪形式贮存的热量利用率为100%,每公斤脂肪含热量41868焦,问此人的体重如何随时间而变化 解:设此人的体重为w ,则根据题意有,每天获取的热量,减去新陈代谢,减去运动消耗的热量,剩余的按利用率100% 转化为脂肪,即有下列等式成立:1046750386941868wdw dt --=经化简有:232313956139565429()41868t t w et e c -=-⋅+假设此人现在的体重为0w ,则此人的体重随时间的变化如下:2323139561395605429()41868t t w et e w -=-⋅+、 生活在阿拉斯加海滨的鲑鱼服从Malthus 增长模型)(003.0)(t p dtt dp = 其中t 以分钟计。
在0=t 时一群鲨鱼来到此水域定居,开始捕食鲑鱼。
鲨鱼捕杀鲑鱼的速率是)(001.02t p ,其中)(t p 是t 时刻鲑鱼总数。
此外,由于在它们周围出现意外情况,平均每分钟有条鲑鱼离开此水域。
(1)考虑到两种因素,试修正Malthus 模型。
(2)假设在0=t 是存在100万条鲑鱼,试求鲑鱼总数)(t p ,并问∞→t 时会发生什么情况解: (1),由题可知, 在考虑两种因素后,修正后的Malthus 模型如下:2()0.003()0.001()0.002dp t p t p t dt=--(2),假设在0t = 时,存在100万条鲑鱼,即(0)1000000p = ,解下列初值问题2()0.003()0.001()0.002(0)1000000dp t p t p t dtp ⎧=--⎪⎨⎪=⎩ 解得0.0010.0012999998()11000001t tae p t a ae --+==-其中当t→∞ 时,2p →。
、 根据罗瑟福的放射性衰变定律,放射性物质衰变的速度与现存的放射性物质的原子数成正比,比例系数成为衰变系数,试建立放射性物质衰变的数学模型。
若已知某放射性物质经时间21T 放射物质的原子下降至原来的一半(21T 称为该物质的半衰期)试决定其衰变系数。
解:假设初始时刻该放射性物质的原子数位0N ,在时间t 时,该放射性物质的原子个数为N ,设衰变系数为k ,则有下列微分方程:0,(0)dNkN N N dt=-= 解得0()kt N t N e =由题可知,当1/2=t T 时,该放射性物质的原子个数下降到原来的一半,即有1/20012kT N N eN == 则有1/2ln 2/k T =-即为该放射性物质的衰变系数。
、 用具有放射性的14C 测量古生物年代的原理是:宇宙线轰击大气层产生中子,中子与氮结合产生14C 。
植物吸收二氧化碳时吸收了14C ,动物食用植物从植物中得到14C 。
在活组织中14C 的吸收速率恰好与14C 的衰变速率平衡。
但一旦动植物死亡,它就停止吸收14C ,于是14C 的浓度随衰变而降低。
由于宇宙线轰击大气层的速度可视为常数,既动物刚死亡时14C 的衰变速率与现在取的活组织样本(刚死亡)的衰变速率是相同的。
若测得古生物标本现在14C 的衰变速率,由于14C 的衰变系数已知,即可决定古生物的死亡时间。
试建立用14C 测古生物年代的模型(14C 的半衰期为5568年)。
解:假设现在取的活组织样本(刚死亡)的衰变速率为0v ,古生物标本现在14C 的衰变速率为0t v ,设动物死亡后,经过时间t 后,动物体内14C 的浓度为()c t 。
再根据上题(题)解得某物质的衰变系数为1/2ln 2/c k T =其中1/2T 为14C 的半衰期,则有()()(),()c dc t v t k N t v t t dt==-为时衰变速度当00tt t ==、时,根据上述公式可得到000c c v v k N N k =-⇒=- ,0000t t c t t cv v k N N k =-⇒=-又因为0()c k t N t N e =,则有00000001lnc c t t k t k t t c c c v v v N N ee t k k k v ==-=-⇒=由题可知1/21/2ln 25568,c T k T ==-,则只要测出现在活组织样本和古生物标本中14C 的衰变速率,代入上式即可估算出古生物标本距今的时间。
、 试用上题建立的数学模型,确定下述古迹的年代:(1)1950年从法国Lascaux 古洞中取出的碳测得放射性计数率为计数(min ⋅g ),而活树木样本测得的计数为计数(min ⋅g ),试确定该洞中绘画的年代; (2)1950年从某古巴比伦城市的屋梁中取得碳标本测得计数率为计数(min ⋅g ),活数标本为计数(min ⋅g ),试估计该建筑的年代。
解: (1),根据上题建立的模型,由已知条件可以确定00 6.68,0.97t v v ==,代入上题模型中可算出001ln 15500t c v t k v == 年(2),同理可得,该古建筑距今的年代001ln 3940t c v t k v == 年、 一容器用一薄膜分成容积为AV 和BV 的两部分,分别装入同一物质不同浓度的溶液。
设该物质分子能穿透薄膜由高浓度部分向低浓度部分扩散,扩散速度与两部分浓度差成正比,比例系数称为扩散系数。
试建立描述容器中溶液浓度变化的数学模型。
设)(l V V B A ==,每隔100s 测量其中一部分溶液的浓度共10次,具体数据为454,499,535,565,590,610,626,650,659,单位为3/m mol 。
试建立扩散系数,并决定2h 后两部分中溶液的浓度各为多少。
解:假设浓度较高的部分为B V ,则测得的十组数据是A V 中溶液浓度的变化,设A V 和B V 中溶液浓度分别为()AC t 和()B C t 。
因为扩散速度与两部分溶液浓度差成正比,则()()A B A dC t k C C dt=-又因为在整个容器中,溶液的浓度是定值,设为0C ,所以02B A C C C =-,代入上式并解得:2220()(2)kt kt A C t e k C t e C -=-⋅+然后用所给的十组数据进行数据拟合,求出上式中的参数。
、 建立耐用消费品市场销售量的模型。
如果已知了过去若干时期销售量的情况,如何确定模型的参数。
解:因为是耐用消费品,所以随着人们对它的拥有量的增加,其销售量()N t 的下降速度与()N t 成正比。
则可建立模型如下:()()dN t kN t dt=- 解上述微分方程得到:()kt N t ce -=根据已有数据用matlab 拟合指数曲线,可确定c k ,。
、 根据经验当一种新产品投入市场后,随着人们对它拥有量的增加,其销售量)(t s 的下降速度与)(t s 成正比。
广告宣传可给销售量添加一个增长速度,它与广告费)(t a 成正比,但广告只能影响这种商品在市场上尚未饱和的部分(设饱和量为M )。
建立销量)(t s 的模型。
若广告宣传只进行有限时间t ,且广告费为常数a ,问)(t s 如何变化解:假设在没有广告宣传的情况下,销售量()s t 的模型为1()()ds t k s t dt=-在加入广告宣传后,销售量()s t 随时间的变化情况如下:120()()()(())t ds t k s t k a t M s x dx dt=-+-⎰其中()ts x dx ⎰为0~t 时间内的销售总量。
如果广告宣传只进行有限时间t,则上述模型变为120001()(())()()tk s t k a M s x dx t t t ds t dt k s t t ⎧-+-≤≤+⎪=⎨⎪-⎩⎰其他时间、 对于技术革新的推广,在下列几种情况下分别建立模型(1)推广工作通过已经采用新技术的人进行,推广速度与已采用新技术的人数成正比,推广是无限的。
(2)总人数有限,因而推广速度随着尚未采用的新技术人数的减少而降低。
(3)在(2)的前提下还要考虑广告等媒介的传播作用。
解:(1),假设推广的人数为()N t ,因为推广是无限的,则()N t 可以达到无限大,建立模型如下()()dN t kN t dt=(2),总人数有限,推广速度随着推广人数()N t 的增加而降低,即推广速度与推广人数成反比,所以建立模型如下:()()dN t kN t dt=-(3),假设投入的广告费随时间的函数为()a t ,广告宣传的影响力与投入的广告费成正比,比例系数为1k ,所以建立模型如下:()1()()dN t k a t kN t dt=-、 某种细菌的增长率不知道,但假设它是常数,试验开始时估计大约有11500个细菌,一时后有2000个,问四时后大约有多少细菌 解:设经过时间t 后细菌数量为()N t ,增长率为常数x 。
()()dN t xN t dt=- 求解上述微分方程,有()xtN t ce-=由题可知,0(0)1150011500N ce c ==⇒=(1)115002000 1.7492x N e x -==⇒= 则有1.7492*4(4)1150010.5203N e -== 个。