邓肯张模型
- 格式:ppt
- 大小:613.00 KB
- 文档页数:22

可编辑修改精选全文完整版3.Duncan-Chang 模型参数的确定实验目的:Duncan 双曲线模型是一种建立在增量广义虎克定律基础上的非线性弹性模型,它在岩土工程界为人们所熟知和广泛应用。
这一类模型可以反映应力应变关系的非线性,参数的物理意义明确和易于确定, 本实验通过对不同围压的控制来模拟模型并确定其参数。
实验原理:点绘()a εσσ~31-曲线,如图3-1所示,Kondner 等人发现,可以用双曲线来拟和这些曲线。
对某一3σ,()a εσσ~31-关系可表示成:aab a εεσσ+=-31 (3-1)渐近线σ3=常量E iE tσ1-σ3(σ1-σ3)uεa 0εa /(σ1-σ3)uεa ba图 3-1 ()a εσσ~31-关系曲线 图3-2 ()a a εσσε--31/关系曲线式中:a 和b 为试验常数。
上式也可以写成:a ab a εσσε+=-31 (3-2)以()31/σσε-a 为纵坐标,a ε为横坐标,构成新的坐标系,则双曲线转换成直线。
见图3-2。
其斜率为b ,截距为a 。
有增量广义虎克定律,如果只沿某一方向,譬如Z 方向,给土体施加应力增量ΔZσ,而保持其他方向的应力不变,可得:E zx σεΔΔ=(3-3) Ev zx σεΔΔ-= (3-4)则 xzE εσΔΔ= (3-5)zxv εεΔΔ-= (3-6)邓肯和张利用上述关系推导出弹性模量公式。
由式(3-5)得:()()aa E εσσεσσεσ∂-∂=-==313111ΔΔΔ (3-7)由此可见虎克定律中所用的弹性模量实际上是常规三轴试验()a εσσ~31-曲线的切线斜率。
这样的模量叫做切线弹性模量,可用t E 表示,见图3-1。
将式(3-1)代入式(3-7),得到:()2a tb a aE ε+= (3-8)由式(3-2)可得:ba a --=311σσε (3-9)式(3-9)代入式(3-8),得: ()[]23111σσ--=b a E t (3-10)由式(3-2)可得:当0→a ε时31→⎪⎪⎭⎫⎝⎛-=a aa εσσε(3-11)而双曲线的初始切线模量i E 为: 031→⎪⎪⎭⎫⎝⎛-=a a i E εεσσ (3-12) 见图3-1。

土体邓肯—张非线性弹性模型参数反演分析土体弹性是土力学和岩土工程研究中最重要的物理量之一,它是分析土壤的受力和强度状态以及土体的力学特性的重要参数。
土体弹性的反演和分析是开发和应用理论模型,评价土体性质和解决工程问题的基础。
在过去几十年中,在土体弹性学研究中,邓肯-张(D-Z)模型被广泛地应用于土壤力学和计算力学中,以定量地描述和分析土体的弹性反应。
邓肯-张(D-Z)模型是以邓肯(Dunkerley)模型为基础,借鉴张(Zhang)模型的结构,对邓肯(Dunkerley)模型进行改进和重新建模得到的。
它将土体弹性关系表达为完全非线性的方式,具有较强的实用性,能够更准确地反映土体弹性特性。
这种完全非线性模型有八个不同的参数,它们分别表示土体的基本特性。
因此,通过定量分析土体弹性参数对土体性质的影响,可以有效评价土体的强度和稳定性,并从而更好地解决工程问题。
本文的目的是基于邓肯-张(D-Z)模型,分析土体弹性参数的反演。
研究的结果表明:八个参数可以采用拟合介质的拟合方法,通过计算完成反演分析。
这样可以对邓肯-张(D-Z)模型参数进行精确拟合,有助于更准确地反演土体性质和弹性参数。
本文采用了统计学和数学方法,使用最小二乘法和拟合介质的拟合方法,反演分析了邓肯-张(D-Z)模型参数,从而提高了参数反演的准确性和稳定性,为岩土工程研究提供了参考依据。
首先,本文介绍了土体弹性的概念和它的重要性,并介绍了邓肯-张(D-Z)模型的拟合方法。
其次,根据统计学和数学方法,介绍了最小二乘法和拟合介质的拟合方法。
最后,本文讨论了邓肯-张(D-Z)模型参数反演分析的结果,总结了参数反演对土体性质和弹性参数的影响,为岩土工程的研究提供参考依据。
从总体上来看,邓肯-张(D-Z)模型具有较强的实用性和准确性,可用于更好地反映和分析土体的弹性特性。
本研究的结果证明,采用最小二乘法,通过拟合介质的拟合方法,可以更准确地反演出土体性质和弹性参数,有助于更好地解决岩土工程中相关问题。


邓肯张本构模型在FLAC3D中的开发与实现一、本文概述随着计算机技术的不断发展和数值模拟方法的日益成熟,岩土工程领域的数值模拟分析已成为研究岩土工程问题的重要手段。
邓肯张本构模型(Duncan-Chang Constitutive Model)作为一种能够描述岩土材料非线性、弹塑性行为的本构模型,在岩土工程领域具有广泛的应用。
然而,在岩土工程数值模拟软件FLAC3D中,邓肯张本构模型并未直接内置,因此需要对其进行开发与实现。
本文旨在探讨邓肯张本构模型在FLAC3D中的开发与实现过程。
将介绍邓肯张本构模型的基本原理和特点,包括其应力-应变关系、屈服准则、硬化法则等。
然后,将详细阐述如何在FLAC3D中通过用户自定义本构模型(User-Defined Constitutive Model)接口实现邓肯张本构模型,包括模型的初始化、应力更新、应变更新等关键步骤。
还将讨论邓肯张本构模型在FLAC3D中的数值实现方法,如如何设置模型参数、如何处理模型的非线性问题等。
通过本文的研究,旨在为FLAC3D用户提供一种在岩土工程数值模拟中应用邓肯张本构模型的有效方法,也为其他岩土工程数值模拟软件的本构模型开发与实现提供借鉴和参考。
本文的研究成果将有助于提高岩土工程数值模拟的准确性和可靠性,推动岩土工程领域的数值模拟研究向更高水平发展。
二、邓肯张本构模型基本理论邓肯张本构模型(Duncan-Chang Model)是一种广泛使用的岩土工程材料本构模型,主要用于描述土的应力-应变关系。
该模型基于土的弹塑性理论,能够模拟土的非线性、弹塑性和剪胀性等行为。
邓肯张本构模型的基本假设包括土的应力-应变关系是非线性的,土的应力路径对其后续行为有影响,以及土的体积变化与其应力状态有关。
模型的核心在于其应力-应变关系的数学描述,其中包括弹性部分和塑性部分。
在弹性部分,邓肯张模型采用了切线弹性模量来描述土的弹性行为,这个模量随着应力的变化而变化,体现了土的非线性弹性特性。
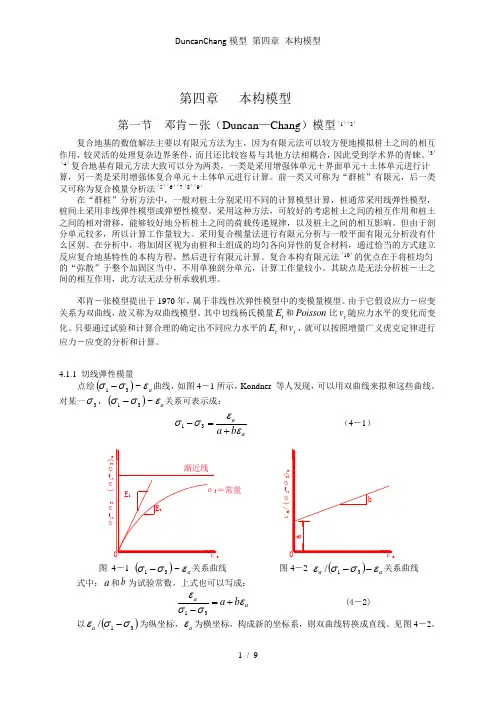
第四章本构模型第一节邓肯-张(Duncan—Chang)模型(1)(2)复合地基的数值解法主要以有限元方法为主,因为有限元法可以较方便地模拟桩土之间的相互作用,较灵活的处理复杂边界条件,而且还比较容易与其他方法相耦合,因此受到学术界的青睐。
(3)其斜率为b ,截距为a 。
有增量广义虎克定律,如果只沿某一方向,譬如Z 方向,给土体施加应力增量ΔZ σ,而保持其他方向的应力不变,可得:E zx σεΔΔ=(4-3) E v zx σεΔΔ-= (4-4)则 x zE εσΔΔ= (4-5)zxv εεΔΔ-= (4-6)邓肯和张利用上述关系推导出弹性模量公式。
由式(4-5)得:()()aa E εσσεσσεσ∂-∂=-==313111ΔΔΔ (4-7) 由此可见虎克定律中所用的弹性模量实际上是常规三轴试验()a εσσ~31-曲线的切线斜率。
这样的模量叫做切线弹性模量,可用t E 表示,见图4-1。
将式(4-1)代入式(3-7),得到:()2a tb a aE ε+= (4-8) 由式(4-2)可得:ba a --=311σσε (4-9)式(4-9)代入式(4-8),得: ()[]23111σσ--=b aE t (4-10) 由式(4-2)可得:当0→a ε时31→⎪⎪⎭⎫⎝⎛-=a aa εσσε (4-11)而双曲线的初始切线模量i E 为:31→⎪⎪⎭⎫ ⎝⎛-=a a i E εεσσ (4-12) 见图4-1。
因此:iE a 1=(4-13) 这里表示a 是初始切线模量的倒数。
在双对数纸上点绘⎪⎭⎫⎝⎛a i P E lg 和⎪⎭⎫ ⎝⎛a P 3lg σ的关系,则近似的为一直线,如图4-3所示。
这里a P 为大气压力。
于是有:na a i P KP E ⎪⎪⎭⎫⎝⎛=3σ (4-14)由式(4-2)还可见,当∞→a ε时()()ua b 313111σσσσε-=-=∞→ (4-15) 试验破坏时的偏应力为()f 31σσ-,则: ()()uf fR 3131σσσσ--=(4-16)f R 叫破坏比将式(4-13),式(4-15),式(4-16)代入式(4-10)得:24.1.2 切线泊松比Kulhawy 和邓肯认为常规三轴试验测得的a ε与()r ε-关系也可用双曲线来拟和,如图4-5所示,点绘a r εε/-与r ε-关系,为一直线,如图4-6所示,其截距为f ,斜率为D ,于是有:可见,()arεε--曲线的切线斜率具有增量泊松比的物理意义,称为切线泊松比,以tv表示。

邓肯-张模型是一个非线性本构模型,既然是一个本构模型,可想而之他反应的是应力与应变之间的关系。
说它是非线性的,那么反映应力应变关系的模量就不是一个常数E那么简单。
在介绍该模型之前,先要介绍一个概念,就是反映非线性关系的增量广义胡克定律: 1123()tt tv d d d d E E σεσσ=-+ (1) 1963年,康纳(Kondner )根据大量土的三轴试验的应力应变关系曲线,提出可以用双曲线拟合出一般土的三轴试验13()~a σσε-曲线,即:13aaa b εσσε-=+ (2)其中,a 、b 为试验常数。
对于常规三轴压缩试验,1a εε=。
邓肯等人根据这一双曲线应力应变关系提出了一种目前被广泛的增量弹性模型,一般被称为邓肯-张(Duncan-Chang )模型。
在常规三轴压缩试验中,13aaa b εσσε-=+可以写成:1113a b εεσσ=+- (3)将常规三轴压缩试验的结果按1113~εεσσ-的关系进行整理,则二者近似成线性关系(见图1)。
其中,a 为直线的截距;b 为直线的斜率。
在常规三轴压缩试验中,由于230d d σσ==,所以切线模量为ε1/(σ1-σ3)1-σ3)ult图11113~εεσσ-线性关系图13211()()t d aE d a b σσεε-==+ (4) 在试验的起始点,10ε=,t i E E =,则:1i E a=,这表明a 表示的是在这个试验中的起始变形模量E i 的倒数。
如果1ε→∞,则: 131()ult bσσ-=(5) 由此可以看出b 代表的是双曲线的渐近线所对应的极限偏差应力13()ult σσ-的倒数。
在土的试样中,如果应力应变曲线近似于双曲线关系,则往往是根据一定的应变值(如115%ε=)来确定土的强度13()f σσ-,而不可能在试验中使1ε无限大,求取13()ult σσ-;对于有峰值点的情况,取1313()()f σσσσ-=-峰,这样1313()()f σσσσ--ult <。

应用MATLAB确定邓肯-张双曲线模型中的K,n参数简介:接合承德中密砂常规三轴试验数据,介绍应用Matlab语言编写计算及绘图程序来处理试验数据的方法,可显著提高试验研究的数据处理效率和结果的可视化程度。
关键字:Matlab 三轴试验邓肯-张模型1 前言基于广义胡克定律的线弹性理论形式简单,参数少,物理意义明确,而且在工程界有广泛深厚的基础,得以应用于许多工程领域中。
早期土力学中的变形计算主要是基于线弹性理论的,只有在计算机得到迅速发展之后,非线性理论模型才得到较广泛的应用。
邓肯-张模型是建立在增量广义胡克定律基础之上的变模量的弹性模型,可以反映土变形的非线性,并在一定程度上反映土变形的弹塑性,很容易为工程界所接受,加之所用参数和材料参数不多,物理意义明确,只需用常规三轴压缩试验即可确定这些参数及材料常数适应的土类比较广,所以该模型为岩土工程界所熟知,并得到了广泛的应用,成为土的最为普及的本构模型之一。
本文主要是应用MATLAB编写计算及绘图程序来处理承德中密砂常规三轴试验数据。
2 基于MATLAB的计算过程实现现场的观测数据经过采集和整理后,按照一定的格式把数据存储在数据文件中,然后可以使用MATLAB丰富的数值运算功能可以非常容易地编制出数据处理程序,先用函数fope n()打开数据文件,fid=fopen(‘filename’,’r’)再用fscanf 函数依次从文件中读取格式化数据来完成对各变量地赋值,其使用语法为:matrix=fscanf(fid,format)。
本文由于数据不是太多,所以在计算过程中没有采取调用存储文件地形式。
直接在计算过程中输入试验数据计算。
2.1 数据的处理对第一组数据,通过编写Matlab语言,由轴向应变和应力差的试验数据可以作出~()和~双曲线关系图形,主要用到的MATLAB命令为:plot(x1,y1);axis([0 0.04 0 3]) ;hold on%(1)plot(x1, x1./y1);a=polyfit(x1, x1./y1,1);t1=0:0.001:0.07;plot(x1, x1./y1,'.',t1,a(1)*t1 +a(2))%(2)其中x1代表第一组轴向应变,x2代表第一组应力差。

研究生课程作业邓肯张模型参数计算学生姓名李俊学科专业岩土工程学号201420105614任课教师周小文教授作业提交日期2014年12月1.计算轴向应变ch h∆∑=1ε式中 1ε-轴向应变;h ∆∑-固结下沉量,由轴向位移计测得0h -土样初始高度c h —按实测固结下沉的试样高度c h ∆—试样固结下沉量2.计算按实测固结下沉的试样高度,面积:式中 Ac -按实测固结下沉的试样面积0V -土样初始体积3.计算剪切过程中试样的平均面积:式中 a A -剪切过程中平均断面积c V -按实测固结下沉的试样的体积i V ∆-排水剪中剪切时的试样体积变化 按体变管或排水管读数求得1h ∆-固结下沉量,由轴向位移计测得 3. 计算主应力差cic h V V A ∆-=01h h V V A c i c a ∆-∆-=Cc c A h V ⨯=1031⨯=-aA CR σσ 式中 31σσ- - 主应力差 1σ―大主应力 3σ-小主应力 C -测力计率定系数 R -测力计读数2 数据处理2.1 3σ=100kPa 数据初步计算当3σ=100kPa 时,各数据初步计算如表1所示。
围压100kPa 数据初步计算表 表12.1.1 由切线模量计算数据 对公式)(311σσε-=a +b 1ε进行直线拟合,如图1所示。
图11131/()~εσσε-拟合曲线 a =0.0002,1i E a==5000kPa b ==0.0028,()131ult bσσ-==263.16kPa ()13f σσ-=204.26kPa ,()()1313f fultR σσσσ-=-=0.77622.1.2 由泊松比计算数据对公式()313/f D εεε-=+-进行直线拟合,如图2所示。
图2 313/~εεε--拟合曲线f=i ν=0.2122 D=2.72972.2 3σ=200kPa 数据初步计算当3σ=200kPa 时,各数据初步计算如表2所示。

土体邓肯—张非线性弹性模型参数反演分析《土体邓肯张非线性弹性模型参数反演分析》是一项重要的科学研究,在这项研究中,研究人员将利用非线性弹性模型的参数反演分析技术,来研究土体的张拉性能。
对于土体的张拉性能,其抗拉强度、塑性性能和力学特征都具有较强的不确定性。
为了克服这种不确定性,非线性弹性模型的参数反演分析技术提供了一种有效的手段,可以在试验过程中获取到准确的参数模型,并进一步深入研究土体的张拉性能。
一、非线性弹性模型的概述非线性弹性模型是一种利用实验测量的参数,结合物理模型的理论模型,用来研究弹性反应的内部结构和行为的模型。
它可以用来描述弹性物质的非线性物性,以及土体张拉时的力学特性。
典型的非线性弹性模型包括邓肯张模型、兰氏莫尔斯模型、HarrisYarwood模型、RiceVangenuchten模型等,其中邓肯张模型是最常用也是最具代表性的模型。
邓肯张模型是一种非线性弹性模型,其物理模型以弹性超塑性为基础,以土体张拉过程中的变形量、压实率及应力量的关系为参数,描述土体张拉过程中的行为特性。
二、参数反演分析技术参数反演分析技术是一种基于回归模型的参数估计的数学方法,可以利用与实验数据相关的模型参数,经过迭代优化,最终得到最佳匹配的参数模型。
非线性弹性模型的参数反演分析技术由实验中获取的非线性参数和迭代优化模型结合而成,可以对非线性弹性模型的参数进行更为准确的反演分析,实现对土体张拉特性和参数之间联系的准确描述。
三、土体邓肯张非线性弹性模型参数反演分析非线性弹性模型的参数反演分析,可以通过试验确定土体张拉过程中的力学特性,并反演出最佳的张拉参数,以深入了解土体的张拉性能。
本文以著名的邓肯张非线性弹性模型为例,通过实验过程,获取相关参数,建立非线性弹性模型,并以最小二乘法、Simplex法等为基础,进行参数反演分析。
经过迭代优化,最终获取到准确的非线性弹性模型参数,从而对土体的张拉性能更为准确的描述。


土体邓肯—张非线性弹性模型参数反演分析近年来,非线性弹性模型在土体力学方面发挥了重要作用,可以提供可靠的分析结果,其中最有代表性的就是邓肯张模型(DuncanZhang model)。
它是由美国土木工程师Duncan和中国科学家Zhang于2003年共同提出的,用于解释和描述土壤弹性行为的力学模型,特别是一维和二维土体行为分析,已经广泛应用于地震工程、地下工程,墙壁结构等领域的研究和实践中。
邓肯张模型的特点是具有更高的非线性程度,而且在模拟分析中具有很高的精度,因此被广泛使用。
土体的非线性弹性参数的反演是土体力学和地质力学分析的基础,如果能够精确地反演出土壤的非线性弹性参数,就能够更加准确地分析出地基土壤的力学性质。
以邓肯张模型为例,参数反演在许多实际应用中发挥了重要作用,但是在参数反演的过程中,由于土壤的非线性性质,传统的拟合方法及其约束条件在反演中往往受到影响,从而导致最终反演精度不高。
为了提高土体邓肯-张模型参数反演的精度,把反演分析模型划分为四个环节:模型选择、模型参数反演、模拟验证和优化调整。
首先,在模型选择环节中,从各种非线性弹性模型中选定最适合当前问题的邓肯-张模型,以保证最终预测精度。
其次,在模型参数反演环节中,采用单级优化的方法进行参数调整,以达到最优的实验结果。
然后,在模拟验证环节中,根据实验结果,采用简单推理和比较分析等方法,对所得模型参数进行检验和验证,以确定模型有效性。
最后,在优化调整环节中,调整模型参数,以便获得准确的模型结果。
通过以上步骤,能够有效地进行邓肯张模型参数反演,提高模型的精确度,使土壤弹性分析的结果更加可靠。
在实践中,采用单级及多级优化的方法可以有效提高邓肯张模型参数反演的精度,使最终的计算结果更加准确,满足实际工程需求。
总之,邓肯张模型具有较高的非线性程度,模拟分析精度较高,广泛应用于地震工程、地下工程、墙壁结构等领域,但其参数反演的过程中受到模型约束条件的影响,反演状态精度不高。
邓肯-张模型开发及其在面板坝计算
中的应用
邓肯-张模型是一种用于计算面板坝的模型,它是由美国土木
工程师邓肯和张在20世纪50年代提出的。
该模型基于坝面的水力学原理,以及坝面的结构特性,建立了一个简单的模型,用于计算面板坝的水力特性。
邓肯-张模型的基本原理是,坝面上的水流可以分解为两个部分:一个是水流的横向分布,另一个是水流的纵向分布。
横向分布的水流可以用一个简单的模型来描述,即水流的流量与坝面的宽度成正比,而纵向分布的水流可以用一个简单的模型来描述,即水流的流量与坝面的高度成正比。
根据邓肯-张模型,可以计算出面板坝的水力特性,包括水流
的流量、水流的速度、水流的压力等。
此外,该模型还可以用来计算面板坝的抗滑性能,以及面板坝的稳定性。
邓肯-张模型在面板坝计算中的应用非常广泛,它可以用来计
算面板坝的水力特性,以及面板坝的抗滑性能和稳定性。
此外,该模型还可以用来计算面板坝的抗滑性能,以及面板坝的稳定性。
此外,该模型还可以用来计算面板坝的抗滑性能,以及面板坝的稳定性。
总之,邓肯-张模型是一种简单而有效的模型,可以用来计算
面板坝的水力特性、抗滑性能和稳定性,在面板坝计算中有着广泛的应用。
邓肯-张EB模型参数求解的二次优化法陈立宏【摘要】邓肯-张非线性弹性模型是土石坝工程中最常用的本构模型.水利行业《土工试验规程》中根据应力水平75%和90%两点法进行计算时,得到的结果往往并不合理,有时n值还可能出现负数.一般的适线法仅仅对单个试样结果进行优化,而并不是针对整组试验结果,因此无法得到最优结果.提出了一种二步优化的参数计算方法,首先对每级围压下单个试样的试验成果采用适线法优化,得到每级围压下的参数a、b.在此基础上,计算得到参数K、n、Rf的初值.然后以邓肯-张理论为基础,根据获得的参数初值针对整组试验成果进行二次优化,以理论计算与试验的应力应变曲线差的平方和最小为目标函数,从而得到EB模型的主要参数.该方法简单实用,能够快速和准确地获得邓肯-张模型参数,并结合糯扎渡大坝堆石料三轴试验数据,对方法进行了验证.%Duncan-Chang nonlinear elastic constitutive model is the most used one in embankment dam engineering.The Specification of Soil Test in hydraulic industry proposes a computational method based on the values of two points from the stress-axial strain curve of the triaxial testing results.The stress levels of these two points are 75% and 90%respectively.However the proposed method cannot obtain reasonable results all the times,and sometimes even the parameter n maybe negative.Curve fitting methods make some progress,but still could not gain the optimal value for the parameters because these methods only based on single sample result.A two step optimization method for acquiring the optimal values of Duncan-Chang model is presented herein.First,the traditional curve fitting method is adopted to obtain thevalues of parameters a and b under each confining pressure.Then the parameters K,n and Rf are ing these parameters as initial values,a second optimization procedure is carried out to fit all the resultsof triaxial test to gain the parameters of Duncan-Chang model,in which,the minimum square sum of the differences of stress and strain curves of theoretical calculation and experiment is taken as the objectivefunction.The method is simple and practical,and can quickly and accurately obtain the parameters of DuncanZhang model.The method is validated based on the triaxial test data of Nuozhadu Dam.【期刊名称】《水力发电》【年(卷),期】2017(043)008【总页数】5页(P52-55,75)【关键词】堆石料;邓肯-张模型;优化方法;土石坝【作者】陈立宏【作者单位】北京交通大学土建学院,北京100044【正文语种】中文【中图分类】TU413堆石料作为高土石坝工程的主体填料,其工程特性和本构模型参数一直为大家所关注。
以土的常三轴实验学习Duncan-Chang本构关系模型一、实验过程1、试样制备试验土样取自于南水北调焦作段一处工程,取回后,人工制成含水量15%的土体。
在实验制样过程中,由于含水量较高,所以在通过制样器后,土柱未能成型,于是在原来土样基础上,添加了较干的土,再在制样器侧壁涂抹凡士林。
最后制成高度7厘米,直径3.5厘米的土柱实验样品2、不固结不排水(UU)剪切试验试验是在土木工程学院深部矿井重点实验室进行的,试验装置如图1所示。
图1 常三轴实验仪主要试验步骤为(1)记录体变管的初始读数;(2)对试样加周围压力,并在周围压力下固结。
当孔隙水压力的读数接近零时,说明固结完成,记下排水管的读数;(3)开动马达,合上离合器,按0.0065%/min的剪切应变速率对试样加载。
按百分表读数为0,30,60,90,120,150,180,210,240,300,360,420,480,540,600,660,⋯,的间隙记读排水管读数和量力环量表读数,直到试样破坏为止。
二、邓肯张双曲线模型到目前为止,国内外学者提出的土体本构模型不计其数,但是真正广泛用于工程实际的模型却为数不多,邓肯-张模型为其中之一。
该模型是一种建立在增量广义虎克定律基础上的非线性弹性模型,可经反映应力~应变关系的非线性,模型参数只有8个,且物理意义明确,易于掌握,并可通过静三轴试验全部确定,便于在数值计算中运用,因而,得到了广泛地应用。
1、邓肯-张双曲线模型的本质邓肯-张双曲线模型的本质在于假定土的应力应变之间的关系具有双曲线性质,见图2(a)。
图2(a ) 12()~a σσε- 双曲线图2(b) 1131/()~εσσε-关系图2 三轴试验的应力应变典型关系理论图1963年,康纳(Kondner )根据大量土的三轴试验的应力应变关系曲线,提出可以用双曲线拟合出一般土的三轴试验13()~a σσε-曲线,即aab a εεσσ+=-31 (1)其中,,a b 为试验常数。