邓肯张模型模拟

可编辑修改精选全文完整版3.Duncan-Chang 模型参数的确定实验目的：Duncan 双曲线模型是一种建立在增量广义虎克定律基础上的非线性弹性模型，它在岩土工程界为人们所熟知和广泛应用。

这一类模型可以反映应力应变关系的非线性，参数的物理意义明确和易于确定， 本实验通过对不同围压的控制来模拟模型并确定其参数。

实验原理：点绘()a εσσ~31-曲线，如图3－1所示，Kondner 等人发现，可以用双曲线来拟和这些曲线。

对某一3σ，()a εσσ~31-关系可表示成：aab a εεσσ+=-31 （3－1）渐近线σ3＝常量E iE tσ1-σ3(σ1-σ3)uεa 0εa /(σ1-σ3)uεa ba图 3－1 ()a εσσ~31-关系曲线 图3－2 ()a a εσσε--31/关系曲线式中：a 和b 为试验常数。

上式也可以写成：a ab a εσσε+=-31 (3－2)以()31/σσε-a 为纵坐标，a ε为横坐标，构成新的坐标系，则双曲线转换成直线。

见图3－2。

其斜率为b ，截距为a 。

有增量广义虎克定律，如果只沿某一方向，譬如Z 方向，给土体施加应力增量ΔZσ，而保持其他方向的应力不变，可得：E zx σεΔΔ=(3－3) Ev zx σεΔΔ-= （3－4）则 xzE εσΔΔ= （3－5）zxv εεΔΔ-= （3－6）邓肯和张利用上述关系推导出弹性模量公式。

由式（3－5）得：()()aa E εσσεσσεσ∂-∂=-==313111ΔΔΔ （3－7）由此可见虎克定律中所用的弹性模量实际上是常规三轴试验()a εσσ~31-曲线的切线斜率。

这样的模量叫做切线弹性模量，可用t E 表示，见图3-1。

将式（3－1）代入式（3－7），得到：()2a tb a aE ε+= （3－8）由式（3－2）可得：ba a --=311σσε （3－9）式（3－9）代入式（3－8），得： ()[]23111σσ--=b a E t （3－10）由式（3－2）可得：当0→a ε时31→⎪⎪⎭⎫⎝⎛-=a aa εσσε（3－11）而双曲线的初始切线模量i E 为： 031→⎪⎪⎭⎫⎝⎛-=a a i E εεσσ （3－12） 见图3－1。

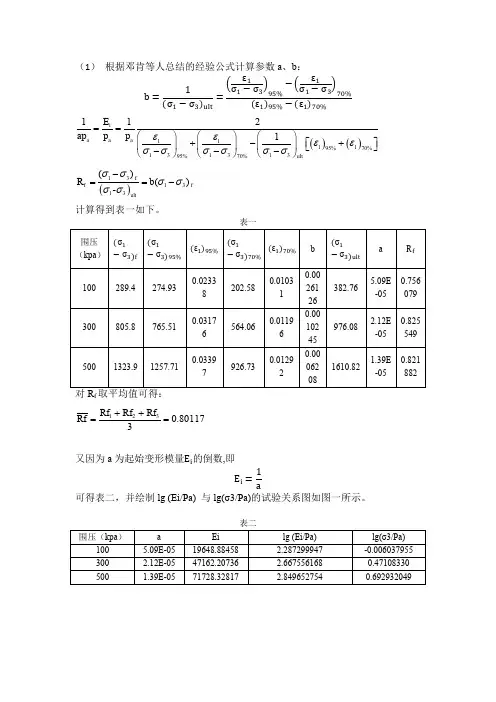
（1） 根据邓肯等人总结的经验公式计算参数a 、b ：()()111195%70%13131395%70%112a 1i a a a ultE p p p εεεεσσσσσσ==⎛⎫⎛⎫⎛⎫⎡⎤+-+ ⎪ ⎪ ⎪⎣⎦---⎝⎭⎝⎭⎝⎭()131313ult()()-ff fR b σσσσσσ-==-计算得到表一如下。

f 80117.03321=++=Rf Rf Rf Rf又因为a 为起始变形模量 的倒数,即可得表二，并绘制lg (Ei/Pa) 与lg( 3/Pa)的试验关系图如图一所示。

表二图一：承德中密砂lg (Ei/Pa) 与lg( 3/Pa)的试验关系图对图一中的试验点进行拟合，得到lg (Ei/Pa) 与lg( 3/Pa)的直线关系：y=0.8033x+2.2914.根据公式：可知K、n分别代表lg (Ei/Pa) 与lg(σ3/Pa)直线的截距和斜率，故可得K=2.2914；n=0.8033。

E-ν法在常规三轴试验中，轴向应变ε1与侧向应变—ε3之间也存在双曲线关系，经变换之后可得如下公式：由上式知—ε3/ε1与—ε3为直线关系，但实际上，二者并不是严格的直线关系，需先对试验结果进行取舍，然后选取某一区间进行拟合。

本文中选取试验曲线的后半部分进行拟合，得到不同围压下相应的拟合曲线，如下图所示。

图二：—ε3/ε1与—ε3关系曲线对应不同围压下的拟合曲线分别为：σ3=100kpa时，y=2.8211x+0.4719；σ3=300kpa时，y=2.8809x+0.4381；σ3=500kpa时，y=3.258x+0.4177.f和D分别为—ε3/ε1与—ε3直线的截距和斜率，结果如下表所示。

又因为νi=f=G-Flg（ 3/Pa）故可做νi—lg（ 3/Pa）关系曲线如下所示。

图三：νi—lg（ 3/Pa）关系曲线G和F分别为νi—lg（ 3/Pa）线性关系曲线的截距和斜率绝对值，由上图可知：G=0.4721；F=0.0765.E-B法：E-B法中引入体变模量B代替切线泊松比,即根据邓肯等人的经验公式：其中,与为达到70%时的偏差应力和体应变的试验值.计算结果如下.变换之后有:其中,和m分别为与直线关系的截距和斜率.由与关系曲线（图四）拟合得到拟合直线为y=1.5089x—3.723. 进而可得：m=1.5089；.图四：与关系曲线。

基于邓肯张模型的基坑开挖数值分析摘要：双排桩式围护结构以其各方面突出的优越性已成为目前应用较为广泛的深基坑支护形式。

与单排桩相比施工简单、成本相近、节约工期，在砂性或粘性土地区，当坑深大于10m时应考虑使用双排桩围护结构。

本文基于Duncan-Chang模型，通过数值模拟的方法研究了开挖深度对变形及内力的影响分析。

得到的规律对双排桩围护结构的施工有一定的指导意义。

关键词：基坑；Duncan-Chang模型；数值模拟；工程应用；引言：随着我国的建设事业蓬勃发展，土地资源也日益紧张，高层和超高层建筑逐渐成为城市建筑的主流，多层的地下建筑也日趋增多，对基坑工程的技术要求显著提高。

高层建筑多建在城市中心区域，因施工场地局限，基坑施工简单放坡较难实现，只能做成陡坡或者垂直坑壁，因此必须依靠围护结构固定坑壁，保证坑内的正常安全作业。

围护结构作为基坑的重要组成部分，其设计和施工成为基坑工程的关键。

[1~2]目前，基坑工程的设计施工仍以经验指导实践为主，但是理论研究相对滞后，尚未形成统一的设计施工规范，因基坑围护结构失效造成的严重事故时有发生，造成人员伤亡和经济损失。

因此，亟待进行更多理论研究、模型测试和工程监测，为基坑工程提供统一完善的理论支撑，保证基坑工程施工安全和经济高效。

[3~4]1 双排桩围护结构双排桩式围护结构以其各方面突出的优越性已成为目前应用较为广泛的深基坑支护形式，在砂性或粘性土地区，当坑深大于10m时应考虑使用双排桩围护结构，与单排桩相比施工简单、成本相近、节约工期。

单排桩在总桩数不变的前提下，以2倍桩距将桩分成两排，前后对齐或错开，桩顶用宽度等于排距的圈梁相连即成为双排桩围护结构。

横剖面相当于门式钢架，侧向刚度很大横向剖面可以视为门式钢架，如图1所示。

（a）三维视图（b）梅花式排桩图1双排桩构造示意图2 基于Duncan-Chang模型的基坑开挖数值分析2.1 计算假定（1）有限元的分析区域不可能为无穷大，根据圣维南原理，基坑工程的影响范围是有限的，因此设定在足够大范围之外土体的变形和内力变化均为零。

在ansys中导入自定义本构模型---邓肯-张模型(转载)邓肯-张模型的关键点是材料的弹性模量随大小主应力差及小主应力(围压)的变化而变化，用APDL实现之的基本思路是：给每个单元定义一个材料号，分级施加荷载，在每个荷载步结束时提取出各单元的大小主应力，据此计算出下个荷载步的弹性模量Et,修改各单元之MP，用于下一步计算。

以下是一个简单算例，copy出去可直接运行。

常规三轴试验模拟by taomingxing,NWPU2003.7.16FINISH/CLEAR/TITLE,Numerical Simulation of three axes testing of soils /PREP7*dim,SUy,array,50 !Settlement records*dim,MaxPs,array,120 !Max history p1-p3*dim,MaxDs,array,120 !Max history Ds!*dim,EEt,array,50 !Et of elememtDuncan-Chang ModelSymbols：c-粘滞力，Fai-内摩擦角，Sf-破坏强度(p1-p3)f，Ds-应力水平，Pa-大气压,P3-围压*CREATE,Duncan-Chang !Creat Macro file*afun,deg !Unit of angle*set,Pa,1e5*set,P1,-ArrS3(i) !注意：岩土工程中应力为拉负压正*set,P3,-ArrS1(i)*if,P3,LT,0.1*Pa,thenP3=0.1*Pa !围压最小取值*endifSf=2*(c*cos(Fai)+P3*sin(Fai))/(1-sin(Fai)) !Mohr-Coulomb破坏强度(p1-p3)fDs=(P1-P3)/Sf !应力水平，*if,Ds,GT,0.95,thenDs=0.95 !应力水平最大取值*endif!判断加卸荷，如果(P1-P3)小于历史最大值视为卸荷－再加荷过程 *if,MaxPs(i),LT,P1-P3,thenEi=k*Pa*(P3/Pa)**nEt=Ei*(1-Rf*Ds)**2 !加荷情况的切线模量MaxPs(i)=P1-P3 !保存历史最大应力*elseif,MaxPs(i),GE,P1-P3Et=Kur*Pa*(P3/Pa)**n !卸荷模量*endifmp,ex,i,Et !修改单元i的Etmp,nuxy,i,Mu*END单元类型et,1,42 !平面四节点单元KEYOPT,1,3,2 !平面应变以下定义材料初始模量mp,ex,1,3.728e7 !砂土的弹性模量mp,nuxy,1,0.33mp,dens,1,1800建立几何模型blc4,0,0,0.08,0.15 !8cm X 15cm /PNUM,AREA,1/REPLOT网格划分aesize,all,0.01mat,1amesh,all边界条件nsel,s,loc,y,0d,all,Uy !底边界竖向约束nsel,s,loc,x,0d,all,Ux !左侧边界水平向约束nsel,all/replotfini/SOLUtime,0.01 !施加围压sfl,all,pres,2e5 !200kPasolve分级施加荷载，实现非线性计算荷载增量10kPa,共50级*DO,ti,1,50取出计算结果，修改弹性模量 /POST1*get,SUy(ti),node,29,u,y !Settlement record of time ti ETABLE,EtabS1,S,1 !取各单元第一主应力ETABLE,EtabS3,S,3 !取各单元第三主应力*dim,ArrS1,array,120*dim,ArrS3,array,120*do,Num,1,120 !Num为单元编号*get,ArrS1(Num),elem,Num,etab,EtabS1 !将单元结果存入数组*get,ArrS3(Num),elem,Num,etab,EtabS3*enddo/PREP7!^^修改砂土单元的Et,单元号1-120c=0 $Fai=35 $Rf=0.7 $k=400 $n=0.6 $Mu=0.33 $Kur=326.7 *do,i,1,120 !各单元循环计算*use,Duncan-Chang,c,Fai,Rf,k,n,Mu,Kur !调用Duncan-Chang宏文件*enddo!EEt(ti)=ET !保存第120单元之ET/SOLUtime,tisfl,3,pres,2e5+1e4*ti !施加荷载，增量1e4solve !对ti级荷载情况求解*ENDDO。

邓肯张本构模型在FLAC3D中的开发与实现一、本文概述随着计算机技术的不断发展和数值模拟方法的日益成熟，岩土工程领域的数值模拟分析已成为研究岩土工程问题的重要手段。

邓肯张本构模型（Duncan-Chang Constitutive Model）作为一种能够描述岩土材料非线性、弹塑性行为的本构模型，在岩土工程领域具有广泛的应用。

然而，在岩土工程数值模拟软件FLAC3D中，邓肯张本构模型并未直接内置，因此需要对其进行开发与实现。

本文旨在探讨邓肯张本构模型在FLAC3D中的开发与实现过程。

将介绍邓肯张本构模型的基本原理和特点，包括其应力-应变关系、屈服准则、硬化法则等。

然后，将详细阐述如何在FLAC3D中通过用户自定义本构模型（User-Defined Constitutive Model）接口实现邓肯张本构模型，包括模型的初始化、应力更新、应变更新等关键步骤。

还将讨论邓肯张本构模型在FLAC3D中的数值实现方法，如如何设置模型参数、如何处理模型的非线性问题等。

通过本文的研究，旨在为FLAC3D用户提供一种在岩土工程数值模拟中应用邓肯张本构模型的有效方法，也为其他岩土工程数值模拟软件的本构模型开发与实现提供借鉴和参考。

本文的研究成果将有助于提高岩土工程数值模拟的准确性和可靠性，推动岩土工程领域的数值模拟研究向更高水平发展。

二、邓肯张本构模型基本理论邓肯张本构模型（Duncan-Chang Model）是一种广泛使用的岩土工程材料本构模型，主要用于描述土的应力-应变关系。

该模型基于土的弹塑性理论，能够模拟土的非线性、弹塑性和剪胀性等行为。

邓肯张本构模型的基本假设包括土的应力-应变关系是非线性的，土的应力路径对其后续行为有影响，以及土的体积变化与其应力状态有关。

模型的核心在于其应力-应变关系的数学描述，其中包括弹性部分和塑性部分。

在弹性部分，邓肯张模型采用了切线弹性模量来描述土的弹性行为，这个模量随着应力的变化而变化，体现了土的非线性弹性特性。

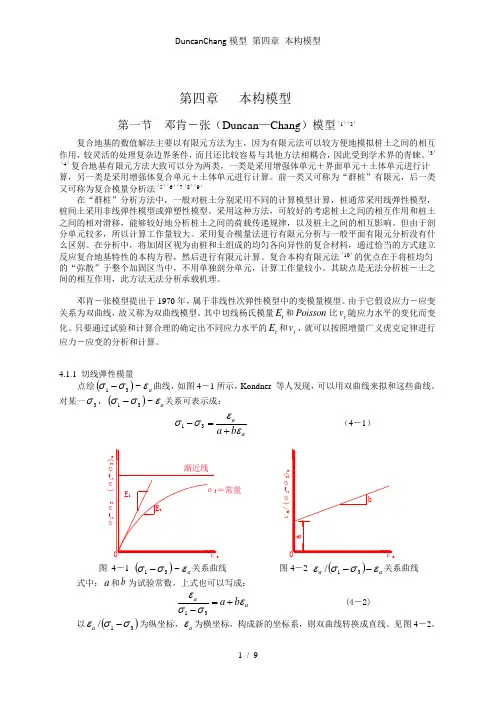
第四章本构模型第一节邓肯－张（Duncan—Chang）模型（1）（2）复合地基的数值解法主要以有限元方法为主，因为有限元法可以较方便地模拟桩土之间的相互作用，较灵活的处理复杂边界条件，而且还比较容易与其他方法相耦合，因此受到学术界的青睐。

（3）其斜率为b ，截距为a 。

有增量广义虎克定律，如果只沿某一方向，譬如Z 方向，给土体施加应力增量ΔZ σ,而保持其他方向的应力不变，可得：E zx σεΔΔ=(4－3) E v zx σεΔΔ-= （4－4）则 x zE εσΔΔ= （4－5）zxv εεΔΔ-= （4－6）邓肯和张利用上述关系推导出弹性模量公式。

由式（4－5）得：()()aa E εσσεσσεσ∂-∂=-==313111ΔΔΔ （4－7） 由此可见虎克定律中所用的弹性模量实际上是常规三轴试验()a εσσ~31-曲线的切线斜率。

这样的模量叫做切线弹性模量，可用t E 表示，见图4-1。

将式（4－1）代入式（3－7），得到：()2a tb a aE ε+= （4－8） 由式（4－2）可得：ba a --=311σσε （4－9）式（4－9）代入式（4－8），得： ()[]23111σσ--=b aE t （4－10） 由式（4－2）可得：当0→a ε时31→⎪⎪⎭⎫⎝⎛-=a aa εσσε （4－11）而双曲线的初始切线模量i E 为：31→⎪⎪⎭⎫ ⎝⎛-=a a i E εεσσ （4－12） 见图4－1。

因此：iE a 1=（4－13） 这里表示a 是初始切线模量的倒数。

在双对数纸上点绘⎪⎭⎫⎝⎛a i P E lg 和⎪⎭⎫ ⎝⎛a P 3lg σ的关系，则近似的为一直线，如图4－3所示。

这里a P 为大气压力。

于是有：na a i P KP E ⎪⎪⎭⎫⎝⎛=3σ （4－14）由式（4－2）还可见，当∞→a ε时()()ua b 313111σσσσε-=-=∞→ （4－15） 试验破坏时的偏应力为()f 31σσ-，则： ()()uf fR 3131σσσσ--=（4－16）f R 叫破坏比将式（4－13），式（4－15），式（4－16）代入式（4－10）得：24.1.2 切线泊松比Kulhawy 和邓肯认为常规三轴试验测得的a ε与()r ε-关系也可用双曲线来拟和，如图4－5所示，点绘a r εε/-与r ε-关系，为一直线，如图4－6所示，其截距为f ，斜率为D ，于是有：可见，()arεε--曲线的切线斜率具有增量泊松比的物理意义，称为切线泊松比，以tv表示。

邓肯－张模型是一个非线性本构模型，既然是一个本构模型，可想而之他反应的是应力与应变之间的关系。

说它是非线性的，那么反映应力应变关系的模量就不是一个常数Ｅ那么简单。

在介绍该模型之前，先要介绍一个概念，就是反映非线性关系的增量广义胡克定律： 1123()tt tv d d d d E E σεσσ=-+ （1） 1963年，康纳（Kondner ）根据大量土的三轴试验的应力应变关系曲线，提出可以用双曲线拟合出一般土的三轴试验13()~a σσε-曲线，即：13aaa b εσσε-=+ （2）其中，a 、b 为试验常数。

对于常规三轴压缩试验，1a εε=。

邓肯等人根据这一双曲线应力应变关系提出了一种目前被广泛的增量弹性模型，一般被称为邓肯－张（Duncan-Chang ）模型。

在常规三轴压缩试验中，13aaa b εσσε-=+可以写成：1113a b εεσσ=+- （3）将常规三轴压缩试验的结果按1113~εεσσ-的关系进行整理，则二者近似成线性关系(见图1)。

其中，a 为直线的截距；b 为直线的斜率。

在常规三轴压缩试验中，由于230d d σσ==，所以切线模量为ε1/(σ1-σ3)1-σ3)ult图11113~εεσσ-线性关系图13211()()t d aE d a b σσεε-==+ （4） 在试验的起始点，10ε=，t i E E =，则：1i E a=，这表明a 表示的是在这个试验中的起始变形模量E i 的倒数。

如果1ε→∞，则： 131()ult bσσ-=（5） 由此可以看出b 代表的是双曲线的渐近线所对应的极限偏差应力13()ult σσ-的倒数。

在土的试样中，如果应力应变曲线近似于双曲线关系，则往往是根据一定的应变值（如115%ε=）来确定土的强度13()f σσ-，而不可能在试验中使1ε无限大，求取13()ult σσ-；对于有峰值点的情况，取1313()()f σσσσ-=-峰，这样1313()()f σσσσ--ult <。

土体邓肯—张非线性弹性模型参数反演分析近年来，非线性弹性模型在土体力学方面发挥了重要作用，可以提供可靠的分析结果，其中最有代表性的就是邓肯张模型（DuncanZhang model）。

它是由美国土木工程师Duncan和中国科学家Zhang于2003年共同提出的，用于解释和描述土壤弹性行为的力学模型，特别是一维和二维土体行为分析，已经广泛应用于地震工程、地下工程，墙壁结构等领域的研究和实践中。

邓肯张模型的特点是具有更高的非线性程度，而且在模拟分析中具有很高的精度，因此被广泛使用。

土体的非线性弹性参数的反演是土体力学和地质力学分析的基础，如果能够精确地反演出土壤的非线性弹性参数，就能够更加准确地分析出地基土壤的力学性质。

以邓肯张模型为例，参数反演在许多实际应用中发挥了重要作用，但是在参数反演的过程中，由于土壤的非线性性质，传统的拟合方法及其约束条件在反演中往往受到影响，从而导致最终反演精度不高。

为了提高土体邓肯-张模型参数反演的精度，把反演分析模型划分为四个环节：模型选择、模型参数反演、模拟验证和优化调整。

首先，在模型选择环节中，从各种非线性弹性模型中选定最适合当前问题的邓肯-张模型，以保证最终预测精度。

其次，在模型参数反演环节中，采用单级优化的方法进行参数调整，以达到最优的实验结果。

然后，在模拟验证环节中，根据实验结果，采用简单推理和比较分析等方法，对所得模型参数进行检验和验证，以确定模型有效性。

最后，在优化调整环节中，调整模型参数，以便获得准确的模型结果。

通过以上步骤，能够有效地进行邓肯张模型参数反演，提高模型的精确度，使土壤弹性分析的结果更加可靠。

在实践中，采用单级及多级优化的方法可以有效提高邓肯张模型参数反演的精度，使最终的计算结果更加准确，满足实际工程需求。

总之，邓肯张模型具有较高的非线性程度，模拟分析精度较高，广泛应用于地震工程、地下工程、墙壁结构等领域，但其参数反演的过程中受到模型约束条件的影响，反演状态精度不高。