基于三轴试验的邓肯—张模型参数的确定方法

可编辑修改精选全文完整版3.Duncan-Chang 模型参数的确定实验目的：Duncan 双曲线模型是一种建立在增量广义虎克定律基础上的非线性弹性模型，它在岩土工程界为人们所熟知和广泛应用。

这一类模型可以反映应力应变关系的非线性，参数的物理意义明确和易于确定， 本实验通过对不同围压的控制来模拟模型并确定其参数。

实验原理：点绘()a εσσ~31-曲线，如图3－1所示，Kondner 等人发现，可以用双曲线来拟和这些曲线。

对某一3σ，()a εσσ~31-关系可表示成：aab a εεσσ+=-31 （3－1）渐近线σ3＝常量E iE tσ1-σ3(σ1-σ3)uεa 0εa /(σ1-σ3)uεa ba图 3－1 ()a εσσ~31-关系曲线 图3－2 ()a a εσσε--31/关系曲线式中：a 和b 为试验常数。

上式也可以写成：a ab a εσσε+=-31 (3－2)以()31/σσε-a 为纵坐标，a ε为横坐标，构成新的坐标系，则双曲线转换成直线。

见图3－2。

其斜率为b ，截距为a 。

有增量广义虎克定律，如果只沿某一方向，譬如Z 方向，给土体施加应力增量ΔZσ，而保持其他方向的应力不变，可得：E zx σεΔΔ=(3－3) Ev zx σεΔΔ-= （3－4）则 xzE εσΔΔ= （3－5）zxv εεΔΔ-= （3－6）邓肯和张利用上述关系推导出弹性模量公式。

由式（3－5）得：()()aa E εσσεσσεσ∂-∂=-==313111ΔΔΔ （3－7）由此可见虎克定律中所用的弹性模量实际上是常规三轴试验()a εσσ~31-曲线的切线斜率。

这样的模量叫做切线弹性模量，可用t E 表示，见图3-1。

将式（3－1）代入式（3－7），得到：()2a tb a aE ε+= （3－8）由式（3－2）可得：ba a --=311σσε （3－9）式（3－9）代入式（3－8），得： ()[]23111σσ--=b a E t （3－10）由式（3－2）可得：当0→a ε时31→⎪⎪⎭⎫⎝⎛-=a aa εσσε（3－11）而双曲线的初始切线模量i E 为： 031→⎪⎪⎭⎫⎝⎛-=a a i E εεσσ （3－12） 见图3－1。

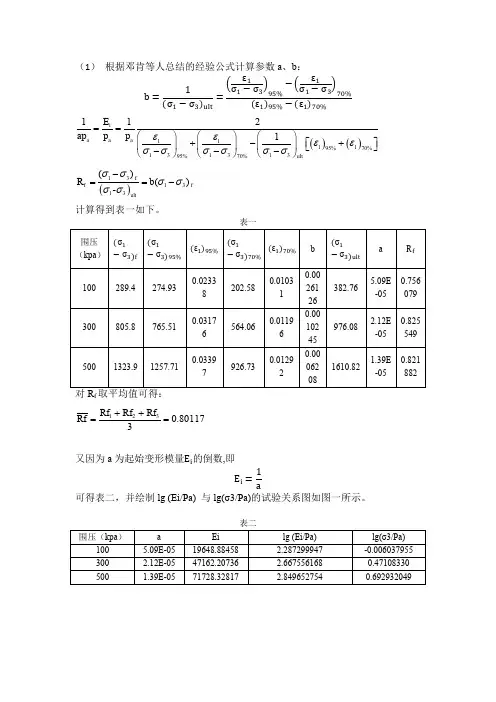
（1） 根据邓肯等人总结的经验公式计算参数a 、b ：()()111195%70%13131395%70%112a 1i a a a ultE p p p εεεεσσσσσσ==⎛⎫⎛⎫⎛⎫⎡⎤+-+ ⎪ ⎪ ⎪⎣⎦---⎝⎭⎝⎭⎝⎭()131313ult()()-ff fR b σσσσσσ-==-计算得到表一如下。

f 80117.03321=++=Rf Rf Rf Rf又因为a 为起始变形模量 的倒数,即可得表二，并绘制lg (Ei/Pa) 与lg( 3/Pa)的试验关系图如图一所示。

表二图一：承德中密砂lg (Ei/Pa) 与lg( 3/Pa)的试验关系图对图一中的试验点进行拟合，得到lg (Ei/Pa) 与lg( 3/Pa)的直线关系：y=0.8033x+2.2914.根据公式：可知K、n分别代表lg (Ei/Pa) 与lg(σ3/Pa)直线的截距和斜率，故可得K=2.2914；n=0.8033。

E-ν法在常规三轴试验中，轴向应变ε1与侧向应变—ε3之间也存在双曲线关系，经变换之后可得如下公式：由上式知—ε3/ε1与—ε3为直线关系，但实际上，二者并不是严格的直线关系，需先对试验结果进行取舍，然后选取某一区间进行拟合。

本文中选取试验曲线的后半部分进行拟合，得到不同围压下相应的拟合曲线，如下图所示。

图二：—ε3/ε1与—ε3关系曲线对应不同围压下的拟合曲线分别为：σ3=100kpa时，y=2.8211x+0.4719；σ3=300kpa时，y=2.8809x+0.4381；σ3=500kpa时，y=3.258x+0.4177.f和D分别为—ε3/ε1与—ε3直线的截距和斜率，结果如下表所示。

又因为νi=f=G-Flg（ 3/Pa）故可做νi—lg（ 3/Pa）关系曲线如下所示。

图三：νi—lg（ 3/Pa）关系曲线G和F分别为νi—lg（ 3/Pa）线性关系曲线的截距和斜率绝对值，由上图可知：G=0.4721；F=0.0765.E-B法：E-B法中引入体变模量B代替切线泊松比,即根据邓肯等人的经验公式：其中,与为达到70%时的偏差应力和体应变的试验值.计算结果如下.变换之后有:其中,和m分别为与直线关系的截距和斜率.由与关系曲线（图四）拟合得到拟合直线为y=1.5089x—3.723. 进而可得：m=1.5089；.图四：与关系曲线。

基于三轴试验的邓肯—张模型参数的确定方法李萼怀;管为华【摘要】Through inducing Duncan-Chang hyperbolic model,the paper obtains the relationship among material parameters.By analyzing triaxial test data,it determines parameters of Duncan-Chang hyperbolic model,which has provided kind of thought for inducing Duncan-Chang model.%通过对邓肯—张双曲线型模型的推导,获取材料参数之间的关系,通过三轴试验数据的分析,确定邓肯—张双曲线模型的参数,为邓肯—张双曲线模型的推导提供了一种思路。

【期刊名称】《山西建筑》【年(卷),期】2012(038)002【总页数】2页(P60-61)【关键词】邓肯—张模型;材料参数;三轴试验【作者】李萼怀;管为华【作者单位】中电投云南国际电力投资有限公司,云南昆明650224;中电投云南国际电力投资有限公司,云南昆明650224【正文语种】中文【中图分类】TU411目前土体的应力和应变分析中，主要有双曲线模型、流变模型、弹塑性模型等，在工程中广泛采用双曲线模型。

该模型理论成熟，应用简便，有较多的实践经验可供参考。

1 双曲线型模型简介［1］图1 双曲线应力应变关系双曲线模型是把三轴压缩试验所得到的应力应变关系近似地认为是双曲线，如图1a)所示。

即在试样的周围压力σ3不变时:其中，a为初始切线模量Ei的倒数;b为主应力差渐近值(σ1－σ3)的倒数;εa为轴向应变。

如果将图1a)的纵轴改为，则双曲线变为直线，如图1b)所示。

从该直线上很容易确定a和b的数值，得到σ3为某一值时的Ei和(σ1－σ3)u。

式(1)可改写为:其中，(σ1－σ3)f为试样破坏时的主应力差;Rf为破坏比，其值小于1，其定义如下:式(2)对轴向应变εa求导数，得到曲线上任一点的切线模量为:式(2)可改写为:由式(4)，式(5)得到:其中，s为应力水平，即实际主应力差与破坏时主应力差的比值，反映抗剪强度发挥的程度根据压缩试验研究，初始切线模量Ei与固结压力σ3的关系可表示如下:其中，k，n均为由试验确定的参数，可从Ei与σ3的关系求得，如图2所示，k 值反映材料的可压缩性;Pa为大气压力，单位与Ei相同，以便使k值成为无因次的数，一般取其近似值为0.1 MPa。

课程名称: 岩土工程测试技术课程编号: S021D05 课程类型: 非学位课考核方式:学科专业: 岩土工程年级: 2007研姓名: 学号:河北工程大学2007～2008学年第二学期研究生课程论文报告三轴压缩试验测定邓肯张模量参数实验报告一. 实验内容测定试样密度、含水量、界限含水率；采用静三轴仪不固结不排水剪试验测不排水强度参数及定邓肯张模量参数。

二. 实验原理1不排水强度参数以主应力差为纵坐标, 轴向应变为横坐标, 绘制主应力差与轴向应变关系曲线。

取曲线上主应力差的峰值作为破坏点, 无峰值时, 取15%轴向应变时的主应力差值作为破坏点。

以剪应力为纵坐标, 法向应力为横坐标, 在横坐标轴以破坏时的应力平面上绘制破损应力圆, 并绘制不同周围压力下破损应力圆的包线（破损应力圆的公切线）, 求出不排水强度参数。

-模型)参数2邓肯张模量(Eν详见《三轴试验原理与应用技术》P117-P122（朱思哲等, 中国电力出版社2003年6月第一版）三. 仪器设备1应变控制式三轴仪: 由压力室、轴向加压设备、周围压力系统、反压力系统、孔隙水压力量测系统、轴向变形和体积变化量测系统组成。

2 附属设备: 包括压样器；环刀、饱和器、切土器、原状土分样器、切土盘、承膜筒和对开圆膜。

3 天平: 称量200g,最小分度值0.01g;称量1000g,最小分度值0.1g。

4 橡皮膜: 弹性乳胶膜, 厚度0.1-0.2mm。

5 透水板：直径与试样相等, 其渗透系数大于试样的渗透系数, 使用前在水中煮沸并泡于水中。

四. 实验步骤1试样制备本试验采用的原状土样, 试样制备, 步骤如下:⑴将土样筒按标明的上下方向放置, 剥去蜡封和胶带, 开启土样筒取出土样。

检查土样结构, 当确定土样已受扰动或取土质量不符合规定时, 舍弃此组土样。

⑵用环刀切取试样时, 在环刀内壁涂一薄层凡士林, 刃口向下放在土样上, 将环刀垂直下压, 并用切土刀沿环刀外侧切削土样, 边压边削至土样高出环刀, 采用钢丝锯或切土刀整平环刀两端土样, 擦净环刀外壁, 称环刀和土的总质量。

邓肯模型参数k、n、R f整理方法研究张波（西安地质矿产勘查开发院，陕西，西安710100.）摘要：对四种石渣料进行三轴CD试验，采用全部法（全部试验点）、70~95法（应力水平70~95%的试验点）及分段法（小应变试验点求参数k、n，应力水平70~95%的试验点求参数R f）三种方法来求取Duncan-Chang模型参数k、n、R f，并采用三种方法求取的参数拟合应变应变曲线与试验曲线对比，研究了不同求取方法的优劣。

结果表明：三轴试验应力应变曲线并不完全符合双曲线关系，ε1/（σ1-σ3）~ε1关系曲线表现出明显的双线性，转折点应变约为1%；石渣料虽然是无粘性土，但其粘聚力并不为零，在工程中应予适当考虑；全部法和70~95法求取的参数拟合曲线与试验曲线较为吻合，拟合效果较好，但考虑到应力应变软化问题，70~95法求取的参数能较好的模拟试验曲线，分段法求取的参数虽然符合物理力学意义，但由于求取参数k、n仅采用小应变的试验点，拟合曲线与试验曲线差别较大，建议采用应力水平70~95%的试验点求取Duncan-Chang 模型参数k、n、R f。

关键词：三轴试验；石渣料；Duncan-Chang模型；应力-应变Duncan model parameters k, n, Rf sorting method/Zhang Bo,(Xi’an Institute of Geological And Mineral exploration,Xi’an Shannxi710100,China)Abstract: The four kinds of gravel material for triaxial CD tests, using all methods (all test points), 70 - 95 method (stress level 70 ~ 95% of test points) and section method (small strain test point demand parameter k , n, the stress level of 70 to 95% of the test points request parameter Rf) are three ways to strike a Duncan-Chang model parameters k, n, Rf, and the use of three methods of parameter fitting to strike a strain-strain curves and test curves comparative study of the pros and cons of different methods to strike.The results showed that: Triaxial stress-strain curve does not fully comply with the h yperbolic relationship, ε1 / (σ1-σ3) ~ ε1 curve showed a clear bilinear, the turning point is about 1% strain; carbide material although no viscous soil, but its cohesion is not zero, the project should be properly taken into account; all law and to strike the law from 70 to 95 parameter fitting curve is more consistent with the experimental curve, fit better, but considering the stress strain-softening problems, 70 to 95 law parameters can strike a better simulation curve, although the parameters of sub-strike law in line with the physical and mechanical sense, but to strike a parameter k, n using only a small strain of test points, the proposed curve together with the experimental curves vary greatly, the stress level is recommended 70 to 95% of the test points to strike Duncan-Chang model parameters k, n, Rf.Keywords: triaxial tests; carbide material; Duncan-Chang model; stress - strain1 引言土的本构模型研究是目前岩土工程的重要课题之一，目前主要有非线性弹性模型及弹塑性模型[1]。

应用MATLAB确定邓肯－张双曲线模型中的K,n参数简介：接合承德中密砂常规三轴试验数据，介绍应用Matlab语言编写计算及绘图程序来处理试验数据的方法，可显著提高试验研究的数据处理效率和结果的可视化程度。

关键字：Matlab 三轴试验邓肯－张模型1 前言基于广义胡克定律的线弹性理论形式简单，参数少，物理意义明确，而且在工程界有广泛深厚的基础，得以应用于许多工程领域中。

早期土力学中的变形计算主要是基于线弹性理论的，只有在计算机得到迅速发展之后，非线性理论模型才得到较广泛的应用。

邓肯－张模型是建立在增量广义胡克定律基础之上的变模量的弹性模型，可以反映土变形的非线性，并在一定程度上反映土变形的弹塑性，很容易为工程界所接受，加之所用参数和材料参数不多，物理意义明确，只需用常规三轴压缩试验即可确定这些参数及材料常数适应的土类比较广，所以该模型为岩土工程界所熟知，并得到了广泛的应用，成为土的最为普及的本构模型之一。

本文主要是应用MATLAB编写计算及绘图程序来处理承德中密砂常规三轴试验数据。

2 基于MATLAB的计算过程实现现场的观测数据经过采集和整理后，按照一定的格式把数据存储在数据文件中，然后可以使用MATLAB丰富的数值运算功能可以非常容易地编制出数据处理程序，先用函数fope n()打开数据文件，fid=fopen(‘filename’,’r’)再用fscanf 函数依次从文件中读取格式化数据来完成对各变量地赋值，其使用语法为：matrix=fscanf(fid,format)。

本文由于数据不是太多，所以在计算过程中没有采取调用存储文件地形式。

直接在计算过程中输入试验数据计算。

2.1 数据的处理对第一组数据，通过编写Matlab语言，由轴向应变和应力差的试验数据可以作出～（）和～双曲线关系图形，主要用到的MATLAB命令为：plot(x1,y1)；axis([0 0.04 0 3]) ；hold on%（1）plot(x1, x1./y1)；a=polyfit(x1, x1./y1,1)；t1=0:0.001:0.07;plot(x1, x1./y1,'.',t1,a(1)*t1 +a(2))%（2）其中x1代表第一组轴向应变，x2代表第一组应力差。

粗粒土三轴试验及邓肯模型参数研究的开题报告一、研究背景与意义粗粒土广泛应用于土力学、地基工程等领域，其三轴试验是粗粒土力学特性研究的基础，对于建立粗粒土力学模型和分析土体应力应变规律具有重要意义。

邓肯模型作为一种经典的粗粒土力学模型，成为了研究粗粒土力学模型的重要工具之一。

因此，对粗粒土三轴试验及邓肯模型参数研究具有重要的理论和实际意义。

二、研究内容和方案本研究拟采用室内常规三轴试验来研究粗粒土在不同固结状态下的力学特性，其中包括MaAnShan粗粒土、长江黄土以及夏邑砂土等。

并基于三轴试验数据，采用邓肯模型对粗粒土的力学行为进行分析，并研究不同邓肯模型参数对其精度的影响。

具体实验方案如下：1. 样品准备：选取不同密度下的MaAnShan粗粒土、长江黄土以及夏邑砂土作为实验材料，并按照标准方法制备土样。

2. 实验步骤：对制备好的土样进行三轴试验，试验条件为不同固结状态、不同应力路径及加载速率等，记录试验数据。

3. 数据分析：基于试验数据，进行邓肯模型参数拟合并分析其敏感性，寻找最优参数组合。

4. 结果分析：通过对试验数据和邓肯模型拟合结果的分析，研究粗粒土的力学行为及该模型在粗粒土力学中的适用性。

三、研究意义和预计成果本研究旨在研究粗粒土的力学特性和邓肯模型的适用性，并为工程实践提供理论支持。

预计可以达到以下成果：1. 确定粗粒土的力学特性及其固结特性。

2. 研究不同固结状态下邓肯模型参数对其精度的影响。

3. 提出邓肯模型在粗粒土力学中的适用性和不足之处。

4. 为今后粗粒土力学特性研究提供参考和借鉴价值。

四、研究进度安排1. 前期准备（2022.01-2022.02）：文献阅读、资料收集、土样制备及实验设备校验等。

2. 实验及数据处理（2022.03-2022.06）：进行实验、处理试验数据，进行邓肯模型参数优化。

3. 结果分析和论文撰写（2022.07-2022.10）：分析实验数据和模型拟合结果，撰写开题报告和论文初稿。

基于三轴试验红层泥岩的邓肯-张模型参数研究罗崇亮;余云燕;包得祥;王鹏【摘要】兰州地区红层泥岩形成于干旱、半干旱环境,其物理力学特性与其他地区的红层泥岩不同。

以G6京藏高速兰海养护维修工程的红层泥岩路基填料为研究对象,通过大量的常规三轴试验,研究含水率对其力学特性及邓肯-张模型参数的影响。

结果表明:在不同含水率下兰州地区红层泥岩的应力-应变曲线关系符合双曲线模型。

含水率小于最优含水率时,破坏形式为剪切破坏;含水率大于最优含水率,破坏形式为鼓状破坏;随着含水率的增加,黏聚力和内摩擦角逐渐减小,内摩擦角减小的幅度更大,究其原因是含水率对黏聚力和内摩擦角的影响机理不同而导致。

采用数学模型进行拟合发现:黏聚力、内摩擦角与含水率分别呈二次抛物线与对数曲线关系。

不同含水率下邓肯-张模型参数破坏比Rf在区间(0.869,0.984)内波动,K值随含水率增大而减小呈负线性关系,n值随含水率的增大而增大呈线性关系。

【期刊名称】《地震工程学报》【年(卷),期】2019(041)002【总页数】9页(P436-444)【关键词】红层泥岩;常规三轴试验;含水率;应力-应变关系;邓肯-张模型参数【作者】罗崇亮;余云燕;包得祥;王鹏【作者单位】[1]兰州交通大学土木工程学院,甘肃兰州730070;[1]兰州交通大学土木工程学院,甘肃兰州730070;[2]兰州交通大学甘肃省轨道交通力学应用工程实验室,甘肃兰州730070;[1]兰州交通大学土木工程学院,甘肃兰州730070;[3]甘肃省交通规划勘察设计院股份有限公司,甘肃兰州730030;[1]兰州交通大学土木工程学院,甘肃兰州730070;【正文语种】中文【中图分类】TU4110 引言红层泥岩在我国西南、西北、华东、中南、华北及东北等地区均有广泛分布[1],就西北、西南地区约有46.516×104 km2。

而甘肃是我国西北红层泥岩的主要分布地区,其红层面积约7.956×104 km2,占甘肃省面积的19.23%[2]。

以土的常三轴实验学习Duncan-Chang本构关系模型一、实验过程1、试样制备试验土样取自于南水北调焦作段一处工程，取回后，人工制成含水量15%的土体。

在实验制样过程中，由于含水量较高，所以在通过制样器后，土柱未能成型，于是在原来土样基础上，添加了较干的土，再在制样器侧壁涂抹凡士林。

最后制成高度7厘米，直径3.5厘米的土柱实验样品2、不固结不排水（UU）剪切试验试验是在土木工程学院深部矿井重点实验室进行的，试验装置如图1所示。

图1 常三轴实验仪主要试验步骤为(1)记录体变管的初始读数；(2)对试样加周围压力，并在周围压力下固结。

当孔隙水压力的读数接近零时，说明固结完成，记下排水管的读数；(3)开动马达，合上离合器，按0.0065%/min的剪切应变速率对试样加载。

按百分表读数为0，30，60，90，120，150，180，210，240，300，360，420，480，540，600，660，⋯，的间隙记读排水管读数和量力环量表读数，直到试样破坏为止。

二、邓肯张双曲线模型到目前为止，国内外学者提出的土体本构模型不计其数，但是真正广泛用于工程实际的模型却为数不多，邓肯-张模型为其中之一。

该模型是一种建立在增量广义虎克定律基础上的非线性弹性模型，可经反映应力～应变关系的非线性，模型参数只有８个，且物理意义明确，易于掌握，并可通过静三轴试验全部确定，便于在数值计算中运用，因而，得到了广泛地应用。

1、邓肯-张双曲线模型的本质邓肯-张双曲线模型的本质在于假定土的应力应变之间的关系具有双曲线性质，见图2（a)。

图2(a ） 12()~a σσε- 双曲线图2（b) 1131/()~εσσε-关系图2 三轴试验的应力应变典型关系理论图1963年，康纳（Kondner ）根据大量土的三轴试验的应力应变关系曲线，提出可以用双曲线拟合出一般土的三轴试验13()~a σσε-曲线，即aab a εεσσ+=-31 （1）其中，,a b 为试验常数。