基于修正剑桥模型的三轴试验仿真模拟
- 格式:pdf
- 大小:467.38 KB
- 文档页数:6

粗粒土大三轴试验研究综述石振明;赵晓伟;彭铭【摘要】Coarse-grained soils are widely distributed in nature.They have a good compaction performance, including high density,strong water permeability,high shear strength,small settlement.They are not easy to produce liquefaction under the earthquake load.They have been widely used in earth dam construction.On the basis of reviewing a large number of related publications,some advances of the research on the coarse-grained soils are summarized in this paper.They include the shear strength,the deformation behaviors,the stress-strain relationship characteristics and several problems in test.The authors presents some of their own thinking,pointing out the direction of future research on the coarse-grained soils according to the existing knowledge.%自然界中广泛分布粗粒土,其具有压实密度大、良好透水性、抗剪强度高、沉降变形小、不易产生地震液化等优良的工程特性,已被广泛运用于土石坝工程建设中。

基于修正剑桥模型分别计算
【实用版】
目录
1.修正剑桥模型简介
2.模型的计算方法
3.模型的应用案例
4.模型的优缺点分析
正文
1.修正剑桥模型简介
修正剑桥模型是一种经济学中的计算模型,主要用于预测和修正实际经济变量与其长期趋势之间的关系。
这一模型由剑桥大学的经济学家们提出,并在实践中得到了广泛应用。
2.模型的计算方法
修正剑桥模型的计算方法分为以下几个步骤:
(1)确定实际经济变量:如 GDP、通货膨胀率、失业率等。
(2)计算长期趋势:通过对历史数据进行回归分析,得出每个变量的长期趋势。
(3)预测未来变量:根据历史数据和长期趋势,预测未来某个时间点的经济变量。
(4)修正预测结果:根据模型的修正因子,对预测结果进行修正,得到最终的预测值。
3.模型的应用案例
修正剑桥模型在许多国家的经济预测和管理中都有应用,例如,我国国家统计局在预测 GDP 时就采用了这一模型。
通过对历史数据的分析和
计算,模型可以预测出未来一段时间内我国 GDP 的增长趋势,为我国政策制定者提供参考。
4.模型的优缺点分析
修正剑桥模型的优点在于,它考虑到了经济变量的长期趋势,因此在预测长期趋势较为稳定经济变量时,预测结果较为准确。
然而,这一模型也存在一些缺点,如在预测短期波动较大的经济变量时,预测结果可能会有较大偏差。
1修正剑桥模型介绍土体本构理论是岩土工程学科的重要基础理论。
随着对土体力学特性的不断深入,塑性理论逐渐被应用于土体本构关系的研究中来。
Roscoe 于1963 年提出著名的剑桥粘土模型,是应用塑性理论的代表,被看做现代土力学的开端,在本构理论研究发展过程中, 各种建模思想不断涌现,出现了各种不同形式的土体本构模型,但弹塑性模型中得到公认的还只有剑桥模型。
现在国际岩土本构的一大发展趋势是又回到剑桥模型,在剑桥模型基础上进行改进和修正,修正剑桥模型是由罗斯科(Roscoe)和伯兰特(Burland)于1968年对剑桥模型作了修正后提出的一个土的弹塑性模型。
主要是对剑桥模型的弹头形屈服面形状作了修正,认为屈服面轨迹应为椭圆。
修正后的模型通常称为修正剑桥模型。
随后又修正了剑桥模型认为在完全状态边界面内土体变形是完全弹性的观点。
认为在完全状态边界面内,当剪应力增加时,虽不产生塑性体积变形,但产生塑性剪切变形。
这可认为是对修正剑桥模型的再次修正。
剑桥模型是英国剑桥大学的Roscoe和Burland根据正常固结粘土和弱超固结粘土的三轴试验,采用状态边界面的概念,由塑性理论的流动法则和塑性势理论,采用简单曲线配合法,建立塑性与硬化定律的函数。
它考虑了静水压力屈服特性、压硬性、剪缩性,但破坏面有尖角,该点的塑性应变方向不易确定。
其假定的弹性墙内加载仍会产生塑性变形。
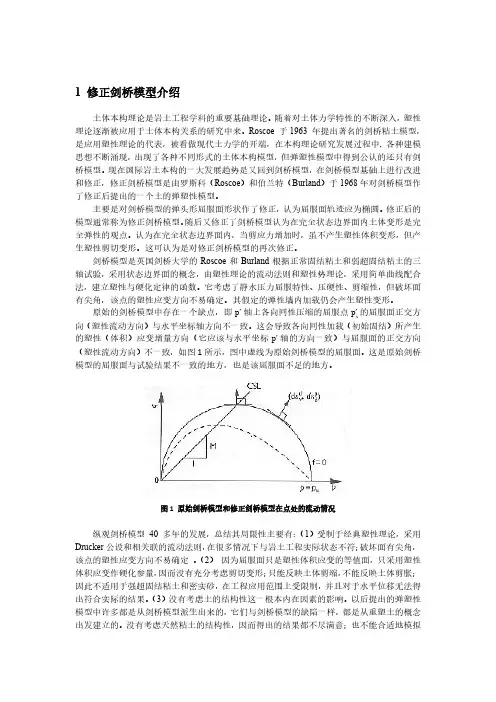
原始的剑桥模型中存在一个缺点,即p'轴上各向同性压缩的屈服点p'的屈服面正交方x向(塑性流动方向)与水平坐标轴方向不一致。
这会导致各向同性加载(初始固结)所产生的塑性(体积)应变增量方向(它应该与水平坐标p'轴的方向一致)与屈服面的正交方向(塑性流动方向)不一致,如图1所示,图中虚线为原始剑桥模型的屈服面。
这是原始剑桥模型的屈服面与试验结果不一致的地方,也是该屈服面不足的地方。
图1 原始剑桥模型和修正剑桥模型在点处的流动情况纵观剑桥模型40 多年的发展,总结其局限性主要有:(1)受制于经典塑性理论,采用Drucker公设和相关联的流动法则,在很多情况下与岩土工程实际状态不符;破坏面有尖角,该点的塑性应变方向不易确定。

饱和粘土的三轴试验此示例是Abaqus中提供的修改后的Cam-clay塑性模型的简单演示。
Cam-clay理论为饱和粘土的实验观察行为提供了合理的匹配,属于Roscoe和他的同事开发的临界状态塑性模型系列(参见Roscoe和Burland-1968以及Schofield和Wroth-1968)。
Abaqus中的Cam-clay模型允许原始Roscoe模型的两个扩展:临界状态湿侧屈服椭圆的“封顶”,以及考虑屈服函数中的第三个应力不变量。
Abaqus理论指南的第 4.4节“非金属的塑性”中记录了对修正Cam-clay理论的这两种扩展。
它们都包含在此示例中。
Abaqus中使用的通用修正Cam-clay屈服函数为其中三个应力不变量是由下式给出的等效压力应力等效剪应力由下式给出其中S为偏应力();和第三个应力不变量,函数中的其他参数为a,临界状态下的等效压力应力值;M,定义临界状态线斜率的材料参数;,a用于在临界状态的湿侧提供不同形状的屈服椭圆的“封顶”参数;g是一个依赖于第三个应力不变量的函数,用于定义压缩和拉伸时的不同屈服面尺寸:其中K是材料参数。
“标准”Cam-clay屈服函数为1。
在屈服面表达式中包含这些参数可以概括该表达式以允许在各种载荷条件下更紧密地匹配数据。
问题描述本例中使用的材料参数如下:弹性参数:对数体积模量,:0.026泊松比,:0.3塑性参数:对数硬化模量,::0.174临界状态比,M:1.0湿帽参数,:0.5第三应力不变参数,K:0.75初始超固结参数,:58.3kN/m2(8.455lb/in2)该示例研究了一个简单的三轴测试:包含在两个光滑压盘之间的轴对称土壤样品,其中一个保持固定,另一个进行规定的垂直运动,拉伸为正,压缩为负。
土样首先通过恒压加载。
然后移动顶板,向下移动以测试三轴压缩或向上移动以测试三轴拉伸。
图 3.2.4-1定义了问题几何。
分析旨在模拟排水三轴试验;因此,它们可以在Abaqus中使用纯位移元素运行。

基于修正剑桥模型模拟理想三轴不排水试验——两种积分算法的对比分析(CZQ-SpringGod )1、修正剑桥模型在塑性功中考虑体积塑性应变的影响,根据屈服面一致性原则,假定屈服函数对硬化参数的偏导为0,就获得了以理想三轴不排水试验为基础的修正剑桥模型屈服函数:22(,)()0c q f p q p p p M =+-= (1) 其中3kkp σ=,ij ij ij s p σδ=-,212ij ij J s s =,q =M 为临界线斜率,c p 为前期固结压力。
硬化/软化法则:p c v c dp v d p ελκ=- (2) 式中p v ε为体积塑性应变,v 为比体积,λ为正常固结线斜率,κ为回弹线斜率。
由于不排水屈服面推导过程是基于硬化参数c p 偏导为0,也就是说不排水试验中硬化参数同体积塑性应变无关,屈服面不变化,而若引入硬化法则就同屈服面推导过程中的假定矛盾,因此计算时将模型处理为理想塑性模型。
2、显式和隐式两种积分格式考虑应变增量ε∆驱动下,第n 增量步到第n+1增量步之间的应力积分格式。
显式积分格式的推导参考文献[1],其中弹塑性矩阵中的塑性硬化模量H=0。
隐式积分格式推导如下:11()n n n p v v p p K εε++=+∆-∆ (3) 111(2)n p n n v c p p ε+++∆=Λ⋅- (4) 12()n n p ij ij ij ij s s G e e +=+∆-∆ (5) 1123n ij p n ij s e M ++∆=Λ (6) 111112(,)()0n n n n n c qf q p p p p M +++++=+-= (7)在这一组方程中没有硬化规律方程表明为理想塑性,并将式(3)-(7)合并化简得到:1112112122(2)06()(1)0n n n n v c n n n trial c p p K K p p G q p p p M Mε++++++⎧--∆+⋅Λ⋅-=⎪⎨+-+Λ=⎪⎩ (8) 式中3(2)(2)2n n trial ij ij ij ij q s G e s G e =+∆+∆ 求解(8)式方程组即可得到n+1增量步的各个增量。


一种改进修正剑桥模型计算精度的算法第卷煤矿开采. 年月 .一种改进修正剑桥模型计算精度的算法郭延华,吴龙海河北工程大学土木工程学院,邯郸摘要和将剑桥模型的屈服面设定为椭圆,得出修正剑桥模型,修正剑桥模型充分利用等向压缩试验曲线,同时只利用了三轴试验中临界状态线,对三轴实验成果利用较少。
本文通过运用修正剑桥模型从理论上计算土体的体积应变和剪切应变,运用三轴试验测出相应土体的体积应变和剪切应变,利用最小二乘法理论拟合理论计算和试验结果的比值,对修正剑桥模型进行改进,得到的弹塑性矩阵改善模型的计算精度。
关键词修正剑桥模型;三轴试验;曲线拟合;计算精度;中图分类号: 文献标识码: . , ,, : ,, ,, . , ,,.: ; ; ;引言出修正系数,代人土的本构模型增量关系式中形成新的弹塑性矩阵刚度矩阵或柔度矩阵 ,从而达到修正剑桥模型是英国剑桥大学的和改进模型计算精度的目的,既验证了剑桥模型的适根据正常固结粘性土和弱超固结粘性土的用性,又充分利用了三轴试验的实验成果。
三轴试验,采用状态边界面的概念,由塑性理论的流动法则和塑性位势理论,利用简单曲线配合法,建立修正剑桥本构模型基本理论塑性与硬化定律的函数。
提出临界状态线、状态边界对修正剑桥模型有面、弹性墙等一系列物理概念,开创了土力学临界状态理论。
经历半个多世纪的发展,国内外许多专家学者对修正剑桥模型进行了一系列改进,如基于经典苏士。
醒理论框架的修正、非关联流动法则、次塑性理论与临界状态理论、有限应变、时间有关、各向异性及结式中: 一 , 、、、一试构性以及循环荷载下的临界状态】等。
验参数,~孔隙比。
在实际工作中,人们发现修正剑桥模型充分利一般岩土体本构模型是在平面上建立的用等向压缩试验曲线,如:土性参数、以及压缩指忽略主应力轴旋转和角的影响,塑性应变增数等,而对三轴试验,则只利用了临界状态线,量与应力一应变增量的关系式为:对三轴试验成果利用较少。
; 由本文通过用修正剑桥模型计算土体的体积应变~和剪应变,根据对应三轴试验结果,拟合两者比值得作者简介郭延华一 ,男,博士,副教授。

非饱和土水力全耦合模型与数值模拟方法研究无论是300m级高坝,还是高陡边坡、大型地下工程建设,均无一例外地涉及复杂赋存环境下岩土体渗流、变形与稳定控制问题。
岩土体渗流与变形的耦合作用以及多场多相耦合过程既是近30年来国际岩土力学领域的前沿研究热点,也是大型水利水电工程、深部岩体工程、核废料地质处置工程等建设中迫切需要解决的关键科学技术难题。
本文以非饱和土为主要研究对象,以土体细观结构及其演化为基础,紧密围绕非饱和土水力耦合机理的量化描述、耦合过程的精细模拟、耦合效应的工程控制这一核心科学问题,重点开展了非饱和土水力全耦合本构模型及数值模拟方法等内容的研究。
主要研究成果如下:(1)建立了考虑颗粒黏结效应的非饱和土弹塑性本构模型大量研究表明,非饱和状态下土体颗粒间的黏结效应对其变形具有显著影响。
采用单位接触面积上弯液面引起的黏结力,定义了黏结因子这一具有严格物理意义的独立变量,用以表征颗粒黏结效应对非饱和土力学特性的影响。
基于试验成果,建立了黏结因子与孔隙比的内在联系,推导了加载一湿陷屈服方程,并在修正剑桥模型的框架下建立了三轴应力状态下非饱和土的弹塑性本构模型。
与经典的巴塞罗那模型(Barcelona Basic Model, BBM)相比,该模型仅采用单一屈服面(BBM有2个),模型参数较少(8个,较BBM少4个参数),且物理意义明确,均可通过常规试验确定。
试验验证结果表明,该模型不仅具备BBM模型所有的描述能力,还能够描述脱湿引起的弹塑性变形等复杂力学特性。
(2)建立了考虑变形效应的土水特性与渗透特性演化模型在水力耦合过程中,土体变形及孔隙分布演化对其土水特性具有显著影响。
尽管土体孔隙分布的演化模式较为复杂,但试验研究表明,土体在变形过程中,孔隙分布的基本形态未发生显著变化、统计分布特征基本不变。
以参考状态孔隙分布函数为基础,经平移和缩放给岀了变形条件下土体的孔隙分布函数,进而建立了考虑变形和滞回效应的土水特征曲线模型。

![[1]杭州软粘土修正剑桥模型参数的分析](https://uimg.taocdn.com/7a978c34eefdc8d376ee32b1.webp)

含砾黏性土力学特性分析韩磊;曹鹏;喻豪俊;刘恩龙【摘要】通过三轴试验,分析研究含砾黏性滑带土的力学特性,发现当砾石含量低时,主要表现出黏性土的力学特性,试样强度较低;砾石含量高时,砾石间的摩擦咬合作用增强,试样强度较高.表现出应变硬化特性,且均表现为剪缩,破坏时试样均是鼓屈变形.随着砾石含量的增加,试样的排水性能先降低后增强.砾石含量较高时,试样的排水性能明显强于砾石含量低的试样与黏性土试样.绘制了四种土样的有效应力路径,低围压时,直线不能很好地包络有效应力路径;黏粒含量低时,强度包线通过原点且是直线,较好的包络了有效应力路径.确定了修正剑桥模型中的M、λ、κ等参数并且对试验结果进行了验证,CD试验计算主应力差与试验结果吻合较好,体应变计算值与试验结果偏差较大,CU试验计算与试验结果较吻合.%The triaxial tests on the viscous slip soils containing gravels are performed to investigate their mechanical properties.It is experimentally found that when the gravels contents are low, the mechanical properties of the mixture soils are weak and their strength is low.The friction and interlock between the gravels enhances with the increasing of the contents of gravels, and the strength of the samples also enhances.Soil samples behave strain hardening, with their volumetric strains decreasing gradually and the samples presenting bulge deformation.With the increasing of the contents of gravels the drainage performance of the samples first decreases and then enhances.The drainage performance of the samples with high gravels contents is better than that of those with low gravel contents.The effective stress paths of four kinds of soils are drawn in the stress plane.Under the low confiningpressure, the straight line cannot envelope the effective stress path well.When the fine contents are low, the envelope is a line through the origin which can envelope the effective stress path.The parameters of M, λandκof the modified Camclay model are determined by the soils samples of triaxial tests.A comparison of CD tests and calculations demonstrates that the principal stress difference is well, but that there are a bit of difference between the calculation results of volumetric strain with the comparisons of CU tests and calculations well.【期刊名称】《西安理工大学学报》【年(卷),期】2018(034)004【总页数】8页(P502-509)【关键词】滑带土;三轴试验;力学特性;修正剑桥模型【作者】韩磊;曹鹏;喻豪俊;刘恩龙【作者单位】国家山区公路工程技术研究中心, 重庆400000;四川大学水利水电学院, 四川成都 610065;国家山区公路工程技术研究中心, 重庆400000;四川大学水利水电学院, 四川成都 610065;国家山区公路工程技术研究中心, 重庆400000;四川大学水利水电学院, 四川成都 610065;国家山区公路工程技术研究中心, 重庆400000;四川大学水利水电学院, 四川成都 610065【正文语种】中文【中图分类】TU43大多数滑坡在滑动体与滑床之间存在一个结构被扰动、破坏的滑动带。
基于修正剑桥模型的筒仓中小麦堆应力分布的有限元计算作者:王颖程绪铎高梦瑶来源:《粮食科技与经济》2020年第01期[摘要]本文应用修正剑桥模型和有限元方法计算平底筒仓中小麦堆的应力分布,计算结果表明:在同一离仓轴径向距离下,筒仓中小麦块的竖直压应力随着粮层深度的增加而增加,但接近仓底与仓壁拐角处反而减小;筒仓中小麦堆的侧向压应力随着粮层深度的增加而增加,但接近仓底中心反而先减小再增加。
在同一深度下,筒仓中小麦堆的竖直压应力随着粮块离仓轴径向距离的增加而减小;筒仓中小麦堆的侧向压应力随着粮块离仓轴径向距离的增加而减小,但是接近仓底处反而增加;筒仓中小麦堆的分层平均竖直压应力与侧向压应力随粮层深度的增加而增加。
筒仓中小麦堆的分层平均侧向压应力与含水率呈负相关,而小麦堆的分层平均竖直压应力与含水率不相关。
[关键词]筒仓;小麦堆;应力分布;修正剑桥模型;有限元方法中图分类号:S512.1 文献标识码:A DOI:10.16465/431252ts.202001小麦储藏在筒仓中承受着重力、摩擦力、仓壁的抵抗力,这些力的作用导致筒仓内小麦堆应力的非均匀分布[1]。
筒仓中储粮的应力分布计算精度直接关系到粮仓的安全性和经济效益。
Janssen[2]提出了一种经典理论,用于预测筒仓内储料的应力分布。
该理论提出了用微层平衡原理计算筒仓中储料的垂直压应力和水平压应力的公式。
但是在Janssen理论中,假设体积密度是恒定的,这导致了对储料应力值的低估[3-4]。
20世纪后期,随着计算机技术的发展,有限元法越来越多地被国际上许多学者应用于筒仓中颗粒材料的应力分布研究[5-7]。
例如,Jofriet J C等[8]采用线弹性模型和有限元方法研究了筒仓中储料的应力分布;Mahmoud A等[9]采用非线性双曲型本构方程和有限元方法,估算了弹性波纹板的圆形筒仓壁的静压力;Bishara A G等[10]应用非线性弹性模型和有限元方法估计了混凝土筒仓壁的静压力。
浅谈土的本构模型发展简介【摘要】随着计算机广泛地用于土力学计算,土的本构模型也被大量的研究。
本文主要介绍现有的土的本构模型。
【关键词】土力学;本构模型土体是一种地质历史产物,具有非常复杂的非线性特征。
在外荷作用下,表现出的应力-应变关系通常具有弹性、塑性、粘性以及非线性、剪胀性、各向异性等性状[1]。
为了较好地描述土的真实性状,建立土的应力-应变-时间之间的关系式,有必要在试验的基础上提出某种数学模型,把特定条件下的试验结果推广到一般情况,这种数学模型称为本构模型[1,2]。
广义上说,本构关系是指自然界-作用与由该作用产生的效应两者之间的关系。
而土的本构关系则是以土为研究对象,以建立土体的应力-应变-时间关系为核心内容,以土体工程问题的模拟和预测为目标,以非线性理论和土质学为基础的一个课题[3]。
1.线弹性模型经典土力学将土体视为理想弹性体,在进行变形计算时采用基于广义虎克定律的线性弹性模型,假定土体的应力和应变关系成正比,通过测定土在不排水条件下的弹性模量E和泊松比μ,或者体积变形模量K和剪切模量G来描述其应力一应变关系。
土的线弹性模型简单,适用于不排水、安全系数较大、土体不发生屈服的情况,工程中可用:(a)计算地基中的垂直应力分布;(b)计算地基在不排水加荷情况下的位移和沉降;(c)基坑开挖问题计算,用于估计基坑在不排水条件下的侧向压力与侧向位移;(d)计算软粘上地基在加荷不排水条件下的沉降和孔隙水压力[5]。
2.非线性模型线弹性模型只适用于安全系数较大、土体不发生屈服的情况。
实际上土体要发生屈服,应力-应变关系是非线性的。
土体发生屈服后除了弹性变形之外还有不可恢复的塑性变形。
因此,实际土体在加荷与卸载时变形的特性是不同的。
土的变形不仅随着荷载的大小而异,而且还与加荷的应力路径有关。
土的这种非弹性的应力-应变关系用弹塑性模型模拟较好,但是弹塑性模型用于实际工程较为复杂,非线弹性模型是为了避免用弹塑性模型的一种方法。
关于修正剑桥模型预测负孔隙水应力的评析张京京;闫澍旺;练继建;郎瑞卿【摘要】在吸力锚和桩靴等海洋基础结构的上拔问题中,负孔隙水应力是抗拔阻力的重要组成部分,开展相关研究具有重要的科学意义和工程价值.修正剑桥模型不但可以合理地解释超静负孔隙水应力产生的机理,而且可以计算三轴卸荷过程中孔隙水应力的发展变化规律.通过开展高岭土地基桶形基础上拔室内模型试验,研究了总上拔力和超孔压随时间的变化情况;结合数值模拟,用修正剑桥模型计算卸荷对负孔隙水应力的影响,分析了上拔过程中负孔压分布特点;总结高岭土土体中受上拔速率影响的上拔承载力试验,并引入归一化速率对试验结果和数值计算结果进行分析,评析并量化了修正剑桥模型在预测负孔隙水应力时的适用条件.研究表明:负孔隙水压力在上拔初期主要集中在桶体下部和内部土体,对应的最大位移出现在桶裙底部;当上拔位移较大时,最大负孔压出现在桶内土体中;随着上拔位移的增大,土体中超静负孔压区域逐渐变大,同时桶形基础外侧土体发生向桶内的水平向位移.修正剑桥模型计算得到的超静负孔隙水应力小于模型试验结果,造成计算误差的主要原因为:剑桥修正计算模型是通过较低速率的三轴试验得到,其速率远远小于模型试验,从而低估了卸荷速率对负孔隙水应力的影响;修正剑桥模型预测负孔压的适用条件为归一化速率低于70.【期刊名称】《天津大学学报》【年(卷),期】2019(052)008【总页数】5页(P871-875)【关键词】修正剑桥模型;负孔隙水应力;适用条件;卸荷【作者】张京京;闫澍旺;练继建;郎瑞卿【作者单位】天津大学水利工程仿真与安全国家重点实验室,天津 300072;中铁十八局集团有限公司,天津 300350;天津大学水利工程仿真与安全国家重点实验室,天津 300072;天津大学水利工程仿真与安全国家重点实验室,天津 300072;天津城建大学土木工程学院,天津 300384【正文语种】中文【中图分类】TU758.11吸附力是一种常见的作用于海洋工程结构物上的外部作用,其作用机理较复杂,是海洋岩土工程学科的重要组成部分.在风和浪等荷载的作用下,位于饱和黏土中的基础结构物处于上拔状态,对应的地基土进入卸荷状态,此时土体内产生负孔隙水压力,该力是吸附力的重要组成部分.负孔压在不同结构物和工程中有多种用途:在吸力锚、吸力桩等结构物中,负孔压可以用于抵抗外荷载;而在桩靴移动、打捞沉船等工程中,负孔压则是需要克服的不利因素. 因此,对负孔压的预测和计算具有重要的工程价值.Li等[1]用有限元法结合修正剑桥模型阐述了负孔隙水应力的产生机理,文献[2-3]则通过三轴试验验证了负孔隙水应力产生机理的合理性.三轴试验、模型试验均表明,速率对负孔隙水应力有重要影响.为了探究修正剑桥模型预测孔隙水应力在模型试验中的应用效果,采用有限元法对桶型基础上拔试验进行模拟,根据分析结果论证该模型预测和计算孔隙水应力的适用性并量化相关适用条件.文献[4-11]开展了大量桶形基础上拔室内模型试验,并对上拔过程中的孔压分布进行了监测.结合以上模型试验和修正剑桥模型,探讨上拔过程中负孔压的预测和计算方法.试验装置由固结试验槽、桶形基础模型和上拔设备等组成.其中,固结试验槽直径为1.0m,高度为1.4m,无缝不锈钢材质.具体模型试验装置见图1.桶形基础模型(见图2)高度为0.40m,外径为0.205m,桶壁厚度为0.0225m,顶部厚度为0.02m.模型内部材料为钢材,外部为混凝土,总重为22.25kg.桶形基础内部净高为0.38m,基础裙底为楔形体,坡度为1∶2.为了便于监测土塞等现象,桶形基础顶部材料为透明的亚格力材料.高岭土使用广泛,但普遍具有固结系数小、渗透性低等特点.本次试验选用高岭土进行.试验用高岭土液限61,塑限38,相对体积质量2.61,灵敏度2.3.试验用土容重和含水率如图3所示.固结压力分别为25kPa和90kPa,固结压力用σc 表示.在预留的孔洞内采用十字板法测量高岭土的不排水强度cu.高岭土的不排水强度cu随深度不断变化,但是在固结桶内的变化非常有限,忽略不计,可认为地基土强度均匀.结合图3可知,25kPa固结压力下土体不排水强度cu为5.7kPa,90kPa固结压力下桶内不排水强度cu为16.7kPa.有限元计算模型(见图4)与试验尺寸相同,孔压测试点A、B埋深分别为20cm、40cm,如图4所示.上拔时固结应力不卸除,计算模型应力状态与试验相同.计算参数见表1.通过观察试验过程可知,试验上拔过程中桶内土体与桶体脱离,发生剪切破坏[11].因此,在数值模拟中,可将桶壁与土体之间的接触设置为可脱离摩擦.根据模型试验反算,侧壁摩擦系数为0.11.上拔承载力试验结果与数值模拟结果对比如图5所示.对比图5中两条曲线可以看出,数值模拟得到的上拔力与试验测得的上拔力较为吻合.通过数值模拟可较为详细地研究上拔过程中孔压的分布.不同上拔位移对应的土体孔压分布见图6.由图6可以看出:当上拔位移较小时,负孔隙水压力主要集中在桶体下部和内部土体,对应的最大位移出现在桶裙底部;当向上位移较大时,最大负孔压出现在桶内土体中;随着桶形基础被不断拔出,土体中超静负孔压区域逐渐变大,同时桶形基础外侧土体发生向桶内的水平向位移.该现象表明,在上拔过程中,桶壁作用于周围土体上的作用不仅有剪切作用,还有水平向卸荷作用,从而导致了负孔压的产生[1-2].对上拔过程中,深度为0.20m和0.40m处的土体孔压变化进行监测.数值计算所得孔压与试验值对比如图7所示.由图7可知,试验测得的孔压与计算值存在一定差异:深度为0.2m处,最大负孔压实测值为-6kPa,而数值模拟值为-1.5kPa;深度为0.4m处,最大负孔压实测值为-10kPa,而数值模拟值为-3.2kPa.由此可见,采用MCC模型计算得到的孔压小于模型试验的实测值.Chen等[12]和Li等[13]的研究表明,卸荷速率对负孔隙水应力有重要影响,卸荷速率越快负孔隙水应力越大,对卸荷速率v、埋深或排水路径H和固结系数Cv进行归一化处理,得到归一化速率V=vH/Cv,并通过分析得到完全不排水、部分排水、完全排水条件的速率界限,如图8所示.由图8可知,根据Chen等[12]的研究结果可将归一化速率为10~1000的试验界定为卸荷时部分排水问题;而若根据Li等[13]的研究结果该速率介于10~100之间.本文中桶形基础模型试验拔出速率v为3.23cm/min,孔压测试点A、B有效排水路径H分别为0.20m和0.40m,试验用高岭土的固结系数Cv为1.5m2/a,则计算得到两点归一化速率V分别为1582、3164.修正剑桥模型根据三轴试验结果建立,为了确定有限元计算模型速率效应的影响作用,对高岭土三轴试验速率进行归一化分析.三轴试样尺寸为14cm×7cm,试验速率0.05%~0.10%/min,高岭土三轴试验归一化速率V为17.0~68.6.结合图8中相关界定数值可知,试验用土常规三轴试验可界定为部分排水状态,而本文中上拔模型试验则属于不排水问题.速率对负孔压值有很大的影响,Chen等[12]和Li等[13]的研究表明,卸荷速率越快则负孔隙水应力越大,三轴试验也验证了这一结论[12].MCC模型是在归一化速率较低三轴试验条件下得到的本构关系,而本文模型试验的归一化速率较高.因此,运用MCC模型计算得到本文试验条件下的孔压结果偏小.当通过较低速率三轴试验得到的本构模型预测并计算土体中负孔压的发展及相应的应力状态时,可能会造成计算结果偏小,低估了负孔压的作用.当三轴试验的加载速率与实际情况相同时,即图8中的完全不排水条件时,运用固结理论考虑速率的影响才能得到与实际工程较为接近的结果.因此,通过常规三轴试验得到的修正剑桥模型较为适用于低速率(对于高岭土为归一化速率小于70)的卸荷问题,而对于归一化速率较大的卸荷问题尚需另做研究.当卸荷速率较快时,模型试验更适用于负孔压预测.采用有限元法研究修正剑桥模型在桶形基础上拔问题中的应用,主要得出以下结论.(1) 采用修正剑桥模型对高岭土地基中桶形基础上拔试验进行分析,数值计算得到的负孔压小于实测值.该现象产生的原因为:修正剑桥模型在较低速率的常规三轴试验中得到,该速率远低于模型试验条件,而卸荷速率越快,负孔隙水应力越大,修正剑桥模型低估了速率对孔压的影响.(2) 修正剑桥模型能够揭示负孔隙水应力的产生机理,但较适用于计算低速卸荷条件下孔压值.对于高岭土,该低速卸荷条件的界限值为70,而对于较高速率的卸荷问题则参考模型试验结果进行预测更为合理.【相关文献】[1] Li X J,Tian Y H,Gaudin C,et al. Comparative study of the compression and uplift of shallow foundations[J]. Computers and Geotechnics,2015,69(5):38-45.[2] Yan S W,Zhang J J,Tian Y H,et al. Pore pressure characteristics in isotropic consolidated saturated clay under unloading conditions[J]. Journal of Marine Science and Technology,2016,24(1):19-25.[3]闫澍旺,张京京,陶琳,等. 等向固结饱和黏土卸荷特性影响因素研究[J]. 岩土工程学报,2016,38(增2):42-47.Yan Shuwang,Zhang Jingjing,Tao Lin,et al. Influencing factors for unloading characteristics in saturated clay[J]. Chinese Journal of Geotechnical Engineering,2016,38(Suppl 2):42-47(in Chinese).[4]闫澍旺,霍知亮,楚剑,等. 黏土中负压桶形基础下沉与承载特性试验及有限元分析研究[J]. 工程力学,2016,33(1):122-132.Yan Shuwang,Huo Zhiliang,Chu Jian,et al. Test and FEA of installation and axial behavior of suction caisson in clay[J]. Engineering Mechanic,2016,33(1):122-132(in Chinese).[5]闫澍旺,霍知亮,孙立强,等. 海上风电机组筒型基础工作及承载特性研究[J]. 岩土力学,2013,34(7):2036-2042.Yan Shuwang,Huo Zhiliang,Sun Liqiang,et al. Study of working mechanism and bearing capacity behavior of bucket foundation for offshore wind turbine [J]. Rock and Soil Mechanics,2013,34(7):2036-2042(in Chinese).[6] Chu J,Yan S W,Li W. Innovative methods for dike construction—An overview[J]. Geotextiles and Geomembranes,2012,30(2):35-42.[7] He J,Chu J,Liu H L. Undrained shear strength of desaturated loose sand under monotonic shearing[J]. Soils & Foundations,2014,54(4):910-916.[8] Guo W,Chu J,Kou H. Model tests of soil heave plug formation in suction caisson[J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering,2016,169(2):214-223.[9] Guo W,Chu J. Experimental study of installation of concrete suction caisson in clay[C]//Proceedings of the Institution of Civil Engineers. San Antonio Texas,USA,2015:784-791.[10] Guo Z,Wang L,Yuan F,et al. Model tests on installation techniques of suction caissons in a soft clay seabed[J]. Applied Ocean Research,2012,34(1):116-125.[11]霍知亮. 黏土地基中桶形基础模型试验及工作机理研究[D]. 天津:天津大学建筑工程学院,2015.Huo Zhiliang. Model Test and Working Mechanism Study of Suction Caisson in Clay[D]. Tianjin:School of Civil Engineering,Tianjin University,2015(in Chinese).[12] Chen R,Gaudin C,Cassidy M J. Investigation of the vertical uplift capacity ofdeep water mudmats in clay[J]. Canadian Geotechnical Journal,2012,49(7):853-865. [13] Li X,Gaudin C,Tian Y,et al. Rate effects on the uplift capacity of skirted foundations on clay[C]// ICPMG 2014-Physical Modelling in Geotechnics. London,UK,2014:473-479.。
基于ABAQUS的红黏土三轴试验数值模拟摘要:目前ABAQUS具有多种岩土体本构关系模型,其中修正剑桥模型以其自身的优越性被广泛应用。
本文选用修正剑桥模型模拟红黏土的三轴压缩试验,试验结果显示应力-应变曲线和孔压-时间关系曲线与实测结果相比具有较好的一致性。
研究成果为红粘土的物理力学特性的研究提供了一定的借鉴意义。
关键词:ABAQUS;本构关系;修正剑桥模型;三轴试验Numerical Simulation of Red Clay Triaxial Test Based on ABAQUSZHANG Xing-shuo,LIU Yang,ZHOU Ze-jiang,GONG Jun-xiang(School of Civil Engineering,Guizhou University Guiyang 550025 China)Abstract:At present,ABAQUS has a variety of geomorphological constitutive models,and the Modified Cambridge model is widely used for its own superiority.In this paper,the Modified Cambridge model is used to simulate the triaxial compression test of red clay,the test results show that the stress-strain curve and the pore pressure-time relationship curve have good consistency with the measured results.The research results provide a certain reference for the study of the physical and mechanical properties of red clay.Keywords:ABAQUS,Constitutive relationship,Modified Cambridge model,triaxial test引言岩土体的应力应变关系通常具有非线性、弹塑性、剪胀性各向异性等特点,试图用一种数学模型反应土体的本构关系等特性是不合理的。
第 3 期水 利 水 运 工 程 学 报No. 3 2023 年 6 月HYDRO-SCIENCE AND ENGINEERING Jun. 2023 DOI:10.12170/20220720002刘翀,傅中志,张意江,等. 堆石料湿化变形特性大型三轴试验研究[J]. 水利水运工程学报,2023(3):138-147. (LIU Chong, FU Zhongzhi, ZHANG Yijiang, et al. Large-scale triaxial test study on wetting deformation characteristics of rockfill materials[J]. Hydro-Science and Engineering, 2023(3): 138-147. (in Chinese))堆石料湿化变形特性大型三轴试验研究刘翀1,傅中志1, 2,张意江1,石北啸1(1. 南京水利科学研究院,江苏南京 210029; 2. 水利部水库大坝安全重点实验室,江苏南京 210029)摘要: 堆石料浸水湿化易导致其和心墙之间变形的不协调,从而在坝顶部位产生纵向裂缝,危害大坝安全。
通过对某水电站筑坝堆石料开展大型三轴压缩试验和三轴湿化试验,分别研究了加载和湿化过程中剪胀比与应力比之间的关系,以及湿化应变与围压和应力水平的关系。
结果表明:湿化试样的峰值强度与初始饱和试样的峰值强度基本相同,即试样湿化时的应力水平对其峰值强度几乎没有影响,但试样的最终体变明显受到湿化时应力水平的影响。
因此,计算土石坝湿化变形宜基于单线法试验;三轴湿化试验时的固结围压和应力水平均对湿化应变具有显著影响,围压越高,湿化体积应变越大,湿化应力水平越高,轴向湿化应变越大,据此提出了一个考虑围压和应力水平影响的湿化应变计算模型;堆石料在加载和湿化过程中服从不同的应力剪胀方程,在构建湿化变形的弹塑性模型时,应采用不同的塑性势函数分别描述堆石料加载应变方向和湿化应变方向。