用修正剑桥模型研究超固结土的变形特性
- 格式:pdf
- 大小:953.82 KB
- 文档页数:5


1修正剑桥模型介绍土体本构理论是岩土工程学科的重要基础理论。
随着对土体力学特性的不断深入,塑性理论逐渐被应用于土体本构关系的研究中来。
Roscoe 于1963 年提出著名的剑桥粘土模型,是应用塑性理论的代表,被看做现代土力学的开端,在本构理论研究发展过程中, 各种建模思想不断涌现,出现了各种不同形式的土体本构模型,但弹塑性模型中得到公认的还只有剑桥模型。
现在国际岩土本构的一大发展趋势是又回到剑桥模型,在剑桥模型基础上进行改进和修正,修正剑桥模型是由罗斯科(Roscoe)和伯兰特(Burland)于1968年对剑桥模型作了修正后提出的一个土的弹塑性模型。
主要是对剑桥模型的弹头形屈服面形状作了修正,认为屈服面轨迹应为椭圆。
修正后的模型通常称为修正剑桥模型。
随后又修正了剑桥模型认为在完全状态边界面内土体变形是完全弹性的观点。
认为在完全状态边界面内,当剪应力增加时,虽不产生塑性体积变形,但产生塑性剪切变形。
这可认为是对修正剑桥模型的再次修正。
剑桥模型是英国剑桥大学的Roscoe和Burland根据正常固结粘土和弱超固结粘土的三轴试验,采用状态边界面的概念,由塑性理论的流动法则和塑性势理论,采用简单曲线配合法,建立塑性与硬化定律的函数。
它考虑了静水压力屈服特性、压硬性、剪缩性,但破坏面有尖角,该点的塑性应变方向不易确定。
其假定的弹性墙内加载仍会产生塑性变形。
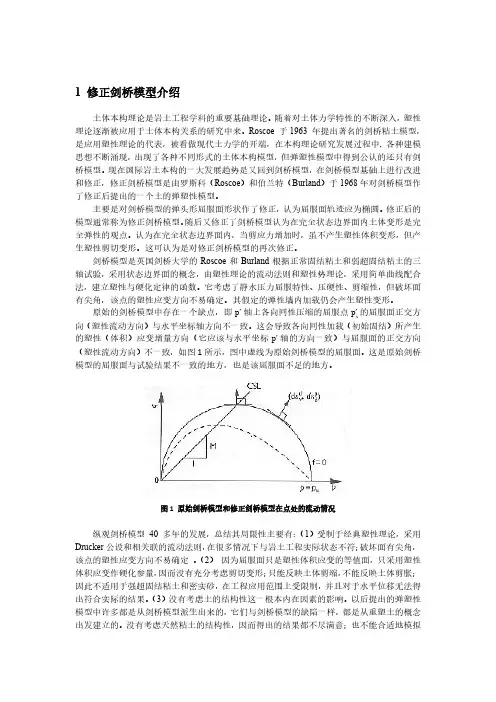
原始的剑桥模型中存在一个缺点,即p'轴上各向同性压缩的屈服点p'的屈服面正交方x向(塑性流动方向)与水平坐标轴方向不一致。
这会导致各向同性加载(初始固结)所产生的塑性(体积)应变增量方向(它应该与水平坐标p'轴的方向一致)与屈服面的正交方向(塑性流动方向)不一致,如图1所示,图中虚线为原始剑桥模型的屈服面。
这是原始剑桥模型的屈服面与试验结果不一致的地方,也是该屈服面不足的地方。
图1 原始剑桥模型和修正剑桥模型在点处的流动情况纵观剑桥模型40 多年的发展,总结其局限性主要有:(1)受制于经典塑性理论,采用Drucker公设和相关联的流动法则,在很多情况下与岩土工程实际状态不符;破坏面有尖角,该点的塑性应变方向不易确定。

浅析ABAQUS中的修正剑桥模型(⼀)摘要问题1:平均主应⼒p'缘何成为CSL的⼀个坐标轴。
问题2:理清各曲线的关系。
1 简单的破坏线q'=Mp'在⼟⼒学中,剑桥模型章节有许多公式、坐标平⾯和曲线,令笔者许多年后依然⽬眩眼花。
浅显的内容易被忽略,复杂的推导却求不得甚解,感觉看得越多熵值越⼤。
这时,不妨回过头看看简单的破坏线q'=Mp'是怎么来的,就算是精神胜利法。
⼟的性质是复杂的,不然也不会搞出来那么多经验公式和本构。
⼟⼒学是基于试验的学科,因为⼟的性质复杂⽆法看透,只能借助试验⼀点点搞起,归纳出⼀些⽚⾯的规律,之后⽤更多的试验来寻找更准确的公式或对前⼈的公式修修补补。
基于对饱和重塑正常固结粘⼟的试验,前⼈在p'-q'平⾯拟合出了破坏线q'=Mp'。
之所以⽤“拟合”,是因为⼟⼒学中的原话是“其关系可近似⽤直线表⽰”,这更体现出试验与各个公式、曲线之间的微妙关系。
偏应⼒q'好理解,就是⼤主应⼒与围压的差值,但平均应⼒p'是⼲什么的,为什么⽤p'当坐标轴⽽⾮其他参数?这或许是个⽆关紧要的问题。
也许前⼈在p'这个位置上试了超多的参数,拟合出的公式或绘制出的曲线都不够优美,所以最后选择了p'。
这就是基于试验和经验的学科,习惯就好。
2 三维坐标系q'-v-p'正常固结曲线NCL位于v-p'平⾯内,q=0,即相当于饱和重塑粘⼟在围压(各向等压)下的e-p曲线。
NCL表⽰在v-lnp'坐标系中表⽰为⼀条直线。
临界状态线CSL是q'为最⼤值各点的连线,是⼀条由⽆数试验拟合出来的空间曲线。
CSL在p'-q'平⾯上的投影是⼀条过原点的直线,即破坏线q'=Mp',在v-p'平⾯上的投影表⽰在v-lnp'坐标系中也是⼀条直线,斜率与NCL 相同。


正常固结黏土本构关系研究综述摘要:正常固结黏土是一种普遍存在于土工和岩土工程中的地质材料,在地基工程和地质灾害评估等领域具有重要作用。
本文通过文献综述的方式总结了已有研究中适用于正常固结黏土的本构模型:Mohr-Coulomb模型、Drucker-Prager模型、Cam-Clay模型、Bingham模型,并对其进行分类评述。
关键词:黏土;本构模型;综述在土壤力学领域中,对于黏土的研究一直是一个重要而又复杂的课题。
黏土是黏性土的典型代表,具强塑性、吸水性、膨胀性、收缩性、吸附性、冻胀性、烧结性、耐火性等特殊性质。
其性质和行为对于工程建设、地质灾害预测与调控等方面具有重要意义[1]。
本构关系指的是描述土体力学性质与其应力-应变关系之间联系的数学模型。
对于正常固结黏土的本构关系研究,旨在揭示黏土在径向和剪切方向上的变形特性。
本综述旨在回顾当前关于正常固结黏土本构关系的研究进展,并对其中涉及的主要观点、方法进行综合概述。
1.Mohr-Coulomb模型土塑性力学理论始于1773年法国科学家库伦提出的Coulomb屈服准则1776年库伦总结土的破坏现象和影响因素,提出土的破坏公式为:根据砂土实验结果得到:对于黏性土,可给出更为普遍的表达式:式中c为内聚力,为内摩擦角。
Mohr-Coulomb模型[2]是基于莫尔-库仑准则的一种用于描述土体和岩石的强度和变形行为的本构模型。
该模型假设土体或岩石在发生破坏时遵循弹塑性行为,其中包括两个主要参数:内聚力和内摩擦角。
内聚力越大,材料越难破坏;内摩擦角越大材料越抗剪切破坏。
应力状态:屈服准则:Mohr-Coulomb模型通过在应力空间中绘制Mohr圆来描述材料的破坏准则。
根据Mohr圆上某一点的位置,可以判断材料处于弹性区还是塑性区,以及是否达到破坏条件。
2.Drucker-Prager模型Drucker等提出在Mohr-Coulomb锥形屈服面上再加上一族强化帽形屈服面。

高等土力学试题(2011)1、饱和土中的渗流和非饱和土中水分迁移规律有哪些相同,哪些不同?孔隙水的移动速率在哪种土中快,为什么?答:二者的相同点:土体中水的流动都服从达西定律;不同点:饱和土中只存在水这一相,而非饱和土中存在水和气两相,他们有各自的渗透流动规律,但气的流动又影响到水的流动,尤其影响到土的固结,也要讨论气的渗透规律。
饱和土中水压力是正值,非饱和土中水压力是负值。
饱和土的渗透系数是常数,非饱和土的渗透系数不是常数;孔隙水率在饱和土中的移动速率快,渗透系数受饱和度的影响,饱和度低,孔隙中气体占据一定的体积,阻碍了水的流动,过水断面面积也缩小,渗透系数就小,孔隙水的移动速率慢。
2、什么叫剪胀性,剪缩性?什么样的土表现为剪胀?什么样的土表现为剪缩?邓肯双曲线模型能否反映剪胀剪缩性?为什么?修正剑桥模型能否反映?答:剪胀性:试样在排水剪试验中体积先减小后增加剪缩性:试验在排水剪试验中体积减小。
强超固结土表现为剪胀,正常固结土和弱超固结表现为剪缩。
邓肯双曲线模型不能反映剪胀剪缩性。
这是因为模型用于广义胡克定律,而胡克定律不可能反映剪胀剪缩性。
对于邓肯张非线性模型,有Eν-与-两种,Eν-模型本身是允许剪胀的,计算所得的泊松比可能大于0.5。
E B-只是有限元计算中,不允许泊松比大于0.5,故模型中不反映剪胀性;E B 模型本身不反映剪胀性。
修正剑桥模型许多情况下能较好反映土的变形特性,它能反映剪缩,但不能反映剪胀。
3、土体有哪些主要变形特性?答:土体的变形是土力学最基本也是最重要的问题,土体变形是复杂的,有些土加荷后立即完成,有些土的变形随时间逐步发展。
随时间发展的变形中又有两部分:一部分是由孔压的消散,即固结变形:另一部分与孔压无关,即使孔压完全消散了,变形仍然随时间而发展,即流变变形。
土的变形是有效应力引起的,有效应力并不是颗粒之间接触点处的实际应力。
通过饱和土有效应力原理和非饱和土的有效应力原理来反映土的一些有效参数,来发现土的一些基本特性。



![[1]杭州软粘土修正剑桥模型参数的分析](https://uimg.taocdn.com/7a978c34eefdc8d376ee32b1.webp)
05年一、一粘土试样在三轴仪中,施加有效应力300kPa 下等向固结,固结完成后等向卸载至有效应力50kPa (状态B )。
在此基础上进行常规排水压缩试验(侧向应力保持不变),使q ′=100kPa (状态C )。
然后试样在不排水条件下 加载至破坏(状态D )。
利用修正剑桥模型分析上述试验。
土的材料参数为:λ=0.16,κ=0.04,Γ=3.0 和M =1.0。
求 (1) 在e~lnp 坐标下绘出正常固结和临界状态线和A →B →C →D 路径; (2) 估计在A →B →C →D 试验过程中q 的峰值; (3) 估计土样破坏时q 的极限值和孔隙比e (状态D )。
(1) 已知:λ=0.16,κ=0.04,Γ=3.0 和M =1.0。
N 与Γ之间的关系为:08.3ln2)04.016.0(0.32ln )(=-+=-+Γ=k N λ 正常固结线(NCL )为: p p N e '-='--=ln 16.008.2ln )1(λ; 临界状态线(CSL )为: p p e '-='--Γ=ln 16.00.2ln )1(λ ; 卸载回弹线(κ线)为:p p p k p N e '-='--='-'---=ln 04.040.1ln 04.068.008.2 ln ln )()1(0κλ修正剑桥模型为:0/222='+''-'M q p p p c,则 030022='+'-'q p p据此可以绘出试样的应力路径(见图1)。
(2)B 点,650/300/=='cc p p 为重超固结土; BC 线的斜率为3.0, 方程为q=3.0(p-50) 所以C 点的3.83='cp kPa ; 代入030022='+'-'q p p ,可解得A →B →C →D 试验过程中q 的峰值为4.134'='cq kPa(3)土体破坏时,见图1中D 点D 点的e 值与C 点的相同,C 点的P=83.3kPa ,代入p e ln 04.040.1-= 求得e=1.22,同理,将e=1.22代入p e ln 16.0000.2-= 求得q=130.3 kPa解法2解:(1)已知:λ=0.16,κ=0.04,Γ=3.0和M=1.0,p’0=300kPa由N=Γ+(λ-κ) ln2得N=Γ+(λ-κ) ln2=3.0+(0.16-0.04)ln2≈3.083∴正常固结线(NCL)方程:v=1+e=N-λln p’,即e= N-1-λln p’= 3.083-1-0.16ln p’ =2.083-0.16 ln p’;临界状态线(CSL)方程:v=1+e=Γ-λln p’,即e=Γ-1-λln p’=3.0-1-0.16ln p’=2.0-0.16ln p’;卸载回弹线(SL )方程:v =1+e = v κ-κln p’= N -(λ-κ)ln p’0-κln p’,即e = N -1-(λ-κ)ln p’0-κln p’=3.083-1-(0.16-0.04)ln300-0.04ln p’ =1.399-0.04ln p’;修正剑桥模型屈服函数为:2222f=M 0p M p p q ''''-+=,代入已知参数得屈服面方程为:223000p p q '''-+=状态A :在有效应力300kPa 下等向固结,所以300A p kPa '=,0A q '=,根据正常固结线(NCL)方程可得:e =2.083-0.16 ln p A ’=1.17。
一、 名词解释1、固结:根据有效应力原理,在外荷载不变的条件下,随着土中超静孔隙水压力的消散,有效应力将增加,土体将被不断压缩,直至达到稳定,这一过程称为~。
单向固结:土体单向受压,孔隙水单向渗流的条件下发生的固结。
2、 固结度:在某一荷载作用下,经过时间t 后土体固结过程完成的程度。
3、 平均固结度:在某一荷载作用下,经过时间t 后所产生的固结变形量与该土层固结完成时最终固结变形量之比称为~。
4、固结系数:反映土的固结特性,孔压消散的快慢,与渗透系数k 成正比,与压缩系数a 成反比,(1)v v wk e C a γ+=⋅5、 加工硬化(应变硬化):正常固结粘土和松砂的应力随应变增加而增加,但增加速率越来越慢,最后趋于稳定。
6、 加工硬化定律(理论):计算一个给定的应力增量引起的塑性应变大小的准则。
7、 加工软化(应变软化):在密砂和超固结土的试验曲线中,应力一般是开始时随应变增加而增加,达到一个峰值后,应力随应变增大而减小,最后趋于稳定。
8、 压硬性:土的变形模量随围压增加而提高的现象。
9、剪胀性:由剪应力引起的体积变化,实质上是由于剪应力引起的土颗粒间相互位置的变化,使其排列发生变化,加大颗粒间的孔隙,从而体积发生了变化。
10、 屈服准则:可以用来弹塑性材料被施加应力增量后是加载还是卸载或是中性变载,即是否发生变形的准则。
屈服准则用几何方法来表示即为屈服面(轨迹)。
11、 流动准则:在塑性理论中,用于确定塑性应变增量的方向或塑性应变增量张量的各个分量间的比例关系的准则,也叫做正交定律。
塑性势面g 与屈服面f 重合(g=f ),称为相适应的~;如果g f ≠,即为不相适应流动规则。
12、 物态边界面:正常固结粘土'p ,'q 和v 三个变量间存在着唯一性关系,所以在 ''p q v --三维空间上形成一个曲面称为~,它是以等压固结线NCL 和临界状态线CSL 为边界的。