反比例函数专题复习公开课总结
- 格式:ppt
- 大小:384.00 KB
- 文档页数:16

第十七章 反比例函数第4课时 反比例函数概念 反比例函数图像函数知识是初中数学的核心内容,本课内容是本学期《反比例函数》的第一、二课时,在同学们学会一次函数之后,接触的另一类新函数,它位居初中阶段三大函数的第二,区别于一次函数,但又建立在一次函数之上,又为以后更高次函数的学习奠定了基础。
所以本节内容有着举足轻重的地位。
理解反比例函数的实际意义,体会反比例函数的不同表示方法,会判断反比例函数,会用待定系数法确定反比例函数的解析式 ,会画出反比例函数图像。
在学生学习了用描点法画函数图象的基础上,学习画反比例函数的图象,其中列表取值很关键。
反比例函数 (k ≠0)自变量的取值范围是x ≠0,所以取值时应对称式地选取正数和负数各一半,并且互为相反数,通常取的数值越多,画出的图象越精确。
连线时要告诉学生用平滑的曲线连接,不能用折线连接。
点击一:反比例函数的概念1.定义:一般地,形如ky x=(k 是常数,0k ≠)的函数为反比例函数.其中自变量x 的取值范围是不等于零的实数. 注意:(1)要能理解反比例函数所表示两个变量的乘积是一个常数; (2)在ky x=中,自变量x 的取值范围是不等于零的实数,且0k ≠;(3)ky x=的表达形式常写成1y kx -=的形式便于应用. 针对练习1:1.当路程s 一定时,速度v 与时间t 之间的函数关系是( ) A.正比例函数 B.反比例函数 C.一次函数 D.以上均不正确2.如果y =122-+k kkx 是反比例函数,k 的值为( )A.k =0;B.k =-21;C.k =0或k =-21;D.k =0且k =-21 3.已知y 与x 成反比例,并且当x =-1时,y =2,那么该函数的解析式为( )A.y =-2x ;B.y =-21x ;C.y =x2- ;D.y =21x4.下列函数中,哪些表示y 是x 的反比例函数?(1)y =43x ;(2)y =x21;(3)xy =6;(4)3x +y =0;(5)x -2y =1;(6)3xy +2=0.5.判断下列两个变量是否成比例?如果成比例,是成正比例,还是成反比例?(1)人的身高y (厘米)与他的年龄x (岁)的关系; (2)圆的面积S (cm 2)与它的半径R(cm)的关系;(3)等腰三角形的顶角y 与底角x 的关系;(4)某人每分钟走200米,则她从家到学校用的时间t(分)与她行走的速度v (米/分)的关系. 6.近视眼镜的度数y (度)与镜片焦距x (米)成反比例,已知400度近视眼镜片的焦距为0.25米,则眼镜度数y 与焦距x 之间的函数关系式是_____________.7.在下列各问题中,函数关系式是一次函数的有 个,是正比例函数的有 个,是反比例函数的有 个.(1)正方形的面积S 与边长x 的函数关系;(2)面积为常数m 的三角形一边长为y 与这条边上的高x 之间的函数关系;(3)一本500页的书,每天看15页,x 天后尚未看完的页数y 与天数x 之间的函数关系; (4)一年期的存款利率为a ,带期后的利息y (元)与存入的金额x (元)之间的关系. 8.写出下列函数关系式:(1)一个矩形面积是20 cm 2,相邻两边长分别为xcm 和ycm ,那么变量y 是x 的函数吗?是反比例函数吗?为什么?(2)某村有耕地360公顷,人口数n 逐年发生变化,那么该村人均占有耕地面积m (公顷/人)是全村人口数n 的函数吗?是反比例函数吗?为什么?(3)北京到上海skm ,一列火车从北京到上海,所用时间t(h)与速度v(km /h)之间的关系是函数关系吗?是反比例函数吗?为什么?9.已知12y y y =+,1y 与x 成正比例,2y 与2x 成反比例,且x=2时,y=0;x=-1时,142y =, 求y 与之间的x 函数关系式.10.已知某电路两端电压不变,当R=12.5Ω时,I=0.2A , 求:(1)I 与R 的函数关系式; (2)当R=5Ω时,求电流强度I ; (3)当I=2A 时,求电阻R .11.如图1,在矩形ABCD 中,AB=2,BC=3,P 是BC 边 上与B 、C 两点不重合的任意一点,设PA=x ,D 点到PA 的距离为y ,求y 与x 之间的函数关系式是 ,自 变量x 的取值范围是 . 答案:1、B ;2、B ;3、C ;4、解:(1)y =43x 不是反比例函数.(2)∵y =x21,∴xy =21.∴y =x 21,是反比例函数.(3)∵xy =6,∴y =x6,是反比例函数.(4)∵3x +y =0,∴y =-3x ,不是反比例函数. (5)∵x -2y =1,∴2y =x -1.∴y =21x -1,不是反比例函数.(6)∵3xy +2=0,∴xy =-32.∴y =x 32-,是反比例函数.5、(1)(2)(3)不成比例;(4)成比例.6、解:∵y 与x 成反比例,∴y =x k ,将x =0.25,y =400代入y =xk,得 400=25.0k ,∴k =100.∴y =x 100,即y 与x 之间的函数关系式是y =x100.7、(1)2s x =,它不是正比例函数,也不是一次函数,也不是反比例函数;图1(2)2my x=是反比例函数;(3)y=500-15x 是一次函数 (4)y=ax 是正比例函数,也是一次函数.所以,应该填2,1,1.8、(1)是,是,因为20y x =;(2)是,是,因为360m n =;(3)是,是,因为s t v=(s 是常数,s≠0). 9、由1y 与x 成正比例,所以可设1y =k 1x ,由2y 与2x 成反比例,所以可设22k y x=,又由于12y y y =+,所以,21k y k x x =+,x=2时,y=0;x=-1时,142y =,所以有2112202142k k k k ⎧+=⎪⎪⎨⎪--=⎪⎩,解得12326k k ⎧=⎪⎨⎪=-⎩,所以y 与之间的x 函数关系式为362y x x =-. 10、(1)由U I R =,可得U=IU=12.5×0.2=2.5,所以 2.5I R=; (2)当R=5Ω时,电流强度I=2.50.55=(A );(3)当I=2A 时,电阻R 2.51.252=(Ω). 11、过D 点作DE⊥PA,垂足为E ,所以△ABP∽△DEA,所以可以得到y=x6.当P 与B 重合时,PA=BA=2,即x=2;当P 与C 重合时,PA=CA=13,即x=13, 所以自变量的取值范围为2<x <13.点击二:反比例函数的图象反比例函数图象的画法是描点法,其步骤是:1.列表:自变量的取值应以O 为中心,沿0的两边取三对以上相反数,分别计算y 的值; 2.描点:先画出一侧,另一侧根据关于原点的对称性去找.3.连线,按从左到右的顺序连接各点,图象的两个分支是断开的,延伸部分有逐渐靠近坐标轴的趋势,但永远不能与坐标轴相交.4.在图象上注明函数的关系式.注意:(1)在连线过程中,应从x 由大到小的顺序用平滑的曲线连接. (2)不能把图象画成与坐标轴相交. 针对练习2:1.在下列函数中,当x 增大时,y 反而减小的函数是( )A.y =31x ;B.y =-x 4;C.y =2x ;D.y =x3 2.已知反比例函数y =xk(k ≠0)的图象过点(-2,1),则它的图象所在的象限是( )A.一、三;B.三、四;C.二、四;D.一、二3.已知点(x 1,-1)、(x 2,-425)、(x 3,-25)在函数y =-x 1的图象上,则下列关系式正确的是( )A.x 1<x 2<x 3;B.x 1>x 2>x 3;C.x 1>x 3>x 2;D.x 1<x 3<x 24.已知y 与x 成反比例,当x =3时,y =4,那么当y =3时,x =_____________.5.已知双曲线11k y x=与直线22y k x =都过点(-2,1),求两个函数解析式,双曲线与直线是否还有其它交点,若有求出这个交点的坐标,若没有请说明情况 6.已知反比例函数y=xk2和一次函数y=2x-1,其中一次函数的图象经过(a,b)、(a+1,b+k)两点.(1)求反比例函数的解析式;(2)如图2,已知点A 在第一象限,且同时在上述两个图象上,求A 点坐标; (3)利用(2)的结果,请问:在x 轴上是否存在点P,使△AOP 为等腰三角形? 若存在,把符合条件的P 点坐标都求出来;若不存在,请说明理由.7.如图3,直线b x y +-=(b >0)与双曲线xky =(k >0)在第一象限的一支相交于A 、B 两点,与坐标轴交于C 、D 两点,P 是双曲线上一点,且PD PO =.(1)试用k 、b 表示C 、P 两点的坐标;(2)若△POD 的面积等于1,试求双曲线在第一象限的一支的函数解析式; (3)若△OAB 的面积等于34,试求△COA 与△BOD 的面积之和. 8.两个反比例函数xy 3=,x y 6=在第一象限内的图象如图4所示, 点P 1,P 2,P 3,…,P 2 005在反比例函数x y 6=图象上,它们的横坐标分别是x 1,x 2,x 3,…,x 2 005,纵坐标分别是1,3,5,…,共2 005个连续奇数,过点P 1, P 2,P 3,…,P 2 005分别作y 轴的平行线,与xy 3=的图象交点依次是Q 1(x 1,y 1),Q 2(x 2,y 2),Q 3(x 3,y 3),…,Q 2 005(x 2 005,y 2 005),则y 2 005= .答案:1、D ;2、C ;3、B ;4、4;5、两交点的坐标为(2,-1)和(-2,1);6、(1)由条件可得b=2a-1,b+k=2(a+1)-1,解得k=2.因此所求的反比例函数解析式为y=x1. (2)由y=x 1,y=2x-1, 得x 1=1,x 2=-21(舍去).从而y=1,所以点A 的坐标为(1,1). (3)若符合条件的点P 存在,①A=2211+=2,OA 与x 轴所夹的锐角为45°. ②若OA 为底,则由∠AOP 1=45°,OA=2,OP 1=P 1A,得OP 1=1,所以点P 1的坐标为(1,0). ③若OA 为腰,AP 为底,则由OP=OA,得P 2(-2,0),P3(2,0). ④若OA 为腰,OP 为底,则由AO=AP=2,得OP=2.所以P 4(2,0).图2图4 图 3因此,这样的点有4个,分别是(1,0),(-2,0),(2,0),(2,0). 7、(1)C (0,b ),D (b ,0),∵PO=PD ,∴22b OD x P ==,b k y P 2=,∴P(2b ,bk2) (2)∵1=∆PODS ,有1221=⋅⋅b k b ,化简得:k =1∴xy 1=(x >0) (3)设A (1x ,1y ),B (2x ,2y ),由AO B CO D BO D CO A S S S S ∆∆∆∆-=+得:34212121221-=+b by bx ,又b x y +-=22得38)(221-=+-+b b x b bx ,即38)(12=-x x b 得[]1924)(212212=-+x x x x b ,再由⎪⎩⎪⎨⎧=+-=x y bx y 1得012=+-bx x ,从而b x x =+21,121=x x ,从而推出0)12)(4)(4(2=++-b b b ,所以4=b .故348-=+∆∆BO D CO A S S . 8、2005y =24009. 点击三:用待定系数法来确定反比例函数的解析式:由于反比例函数ky x=中只有一个待定系数,因此只要一对对应的x 、y 值,或已知其图象上一个点的坐标即可求出k ,进而确定反比例函数的表达式.点击四:正确理解反比例函数表达式中k 的几何意义:如图1,过双曲线ky x=上任意一点P(x ,y)作x 轴,y 轴的垂线PM 、PN ,所得矩形PMON 的面积S=PM •PN=|x |•|y|,而ky x=,所以x y=k ,所以S=|x y|=|k|.即过双曲线上用意一点作x 轴,y 轴的垂线所得矩形的面积为|k|.点击五:函数图像一次函数和反比例函数是两类重要的函数,也是考试的热点内容.在各类考试中,常常出现两类函数的图象融合在一起的题目针对练习:1.(2007 福建龙岩市)函数y x m =+与(0)my m x=≠在同一坐标系内的图象可以是( ).xyO xyO xyO xyO2. 函数1y kx =+与函数ky x=在同一坐标系中的大致图象是下图中的 ( )3.正比例函数kx y 2=与反比例函数xk y 1-=在同一坐标系中的图象不可能是( )答案:1.B; 2.A; 3.D.类型之一:反比例函数的意义例1 若函数y=(m 2-1)x235m m +-为反比例函数,则m=________.【解析】在反比例函数y=k x中,其解析式也可以写为y=k ·x -1,故需满足两点,一是m 2-1≠0,二是3m 2+m-5=-1 【点评】函数y=kx为反比例函数,需满足k ≠0,且x 的指数是-1,两者缺一不可. 答案:m=43- 类型之二:反比例函数图象例2 已知P 1(x 1,y 1),P 2(x 2,y 2),P 3(x 3,y 3)是反比例函数y=•的图象上的三点,且x 1<x 2<0<x 3,则y 1,y 2,y 3的大小关系是( )A .y 3<y 2<y 1B .y 1<y 2<y 3C .y 2<y 1<y 3D .y 2<y 3<y 1 【解析】反比例函数y=2x的图象是双曲线、由k=2>0•知双曲线两个分支分别位于第一、三象限内,且在每一个象限内,y 的值随着x 值的增大而减小,点P 1,P 2,P 3•的横坐标均为负数,故点P 1,P 2均在第三象限内,而P 3的第一象限.故y>0.•此题也可以将P ,P ,P 三点的横坐标取特殊值分别代入y=2x中,求出y 1,y 2,y 3的值,再比较大小.xy O B . xyO D .O xyC .xy O A . x yx yx yxyADC B答案:C例3 如图,一次函数y=kx+b 的图象与反比例函数y=mx图象交于A (-2,1),B (1,n )两点.(1)求反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值大于反比例函数的值的x 的取值范围.【解析】(1)求反比例函数解析式需要求出m 的值.把A (-2,1)代入y=m x中便可求出m=-2.把B (1,n )代入y=2x-中得n=-2.由待定系数法不难求出一次函数解析式.(2)认真观察图象,结合图象性质,便可求出x 的取值范围. 答案:(1)y=-2x,y=-x-1 (2)x<-2或0<x<1 类型之三:确定函数关系式例1 已知函数43m y mx +=是反比例函数,试求出m 的值,并写出函数关系式. 解析:此类问题,一般采用反比例函数的另一种表达方式)0(1≠=-k kx y 来列式求解. 由题意得:m+4=-1,解得m =-5.将m 值代入得函数关系式15y x=-. 例2 已知反比例函数的图象经过点(-3,4),则此函数关系式是 . 解析:将点(-3,4)代入xk y =,得k =-12,所以此函数关系式为.12x y -=例3 如图(1)所示的函数图象的关系式可能是 ( ). A . y =x B . y x 1=C . y =x 2D . y =||1x 解析:由图象知,x >0或x <0时,y >0,只有D 符合,故选D .例4 一个反比例函数在第三象限的图象如图(2),若A 是图象上任意一点,AM ⊥x 轴于M ,O 是原点,如果△AOM 的面积是5,求这个反比例函数的解析式.解析:此题除了利用△AOM 的面积等于||21k 外,还要用双曲线的 位置确定k 的符号.因为||21k =5,所以|k |=10,又因为双曲线在第三象限,所以k >0,所以k =10.所以xy 10=.例5 正比例函数y =x 的图象与反比例函数xky =的图象有一个交点的纵坐标是2, 求反比例函数的解析式.解析:由题意将y =2代入y =x 中求出x =2,得出交点(2,2),将(2,2)代入xky =得k =4,所以反比例函数解析式为xy 4=. 类型之四:函数图像Ax y图(2) O M例1(2007滨州市)如图1,点P 为反比例函数2y x=上的一动点,作PD x ⊥轴于点D ,POD △的面积为k ,则函数1y kx =-的图象为( )析解:设P 点坐标为(b a ,),因为P 点在反比例函数2y x=图象上,所以a b =2,又因为P 点在第一象限,所以POD △的面积为k =21a b =1,则一次函数的解析式为y=x-1,它的图象与两坐标轴的交点分别是(1,0)和(0,-1),应选(A ).例2(2007深圳市)在同一直角坐标系中,函数(0)ky k x=≠与(0)y kx k k =+≠的图象大致是( )解析:在同一坐标系中,同时确定一次函数与反比例函数的图象,解答这类问题一般 使用排除法,对每一个选项进行讨论.先根据选项中其中一个函数图象的位置特点确定k 的符号,再根据k 的符号确定另一个函数图象的位置.在选项(A)与(C)中,由反比例函数的图象知k >0,则一次函数(0)y kx k k =+≠的图象应当过第一、二、三象限,(A)中的一次函数图象不合题意,(C)中的一次函数图象符合题意;在选项(B)与(D)中由反比例函数的图象知k <0,则一次函数(0)y kx k k =+≠的图象应当过第二、三、四象限,但(B)与(D)中的一次函数图象都不符合题意.故答案选(C).类型之五:“点”在反比例函数的图象上所谓点在反比例函数的图象上,也就是反比例函数的图象经过该点,则该点的坐标一定满足其解析式.例1在ABC △的三个顶点(23)(45)(32)A B C ----,,,,,中,可能在反比例函数(0)ky k x=>的图象上的点是 .解析:由反比例函数ky x=知,k xy =.∵0k >,∴若点(,)x y 在该函数的图象上,需横坐标与纵坐标同号.则只有点B 满足.图1 x yP0 D A . x y0 1 1-B . xy 01 1- C .x y11 D .xy1-1-A. x y B. x y C. x y D. x y例2下列函数中,图象经过点(11)-,的反比例函数解析式是( )(A )1y x=(B )1y x-=(C )2y x=(D )2y x-=解析:设该函数解析式为k y x =,由题可得k xy ==-1,∴该反比例函数解析式为1y x-=,应选(B ). 例3已知反比例函数的图象经过点(3,2)和(m ,-2),则m 的值是__. 解析:解答本题应先求函数解析式.由题可得6k =,∴该函数的解析式为6y x=.把(m ,-2)代入6y x =,得62m-=,3m =- 例4反比例函数6y x=-图象上一个点的坐标是 .解析:本题是一道开放性试题,答案不唯一,只要满足条件6xy =-的任一点()x y ,均可. 例5若反比例函数1y x=-的图象上有两点1(1)A y ,,2(2)B y ,,则1y ______2y (填“>”或“=”或“<”).解析:本题考查反比例函数图象的性质。


人教版九年级数学下册:26.小结——《反比例函数》复习说课稿1一. 教材分析《人教版九年级数学下册》第26节是小结章节,主要是对反比例函数的复习。
本节课的内容包括反比例函数的定义、性质、图象和解析式等。
通过本节课的学习,学生能够掌握反比例函数的基本概念,理解反比例函数的性质,能够运用反比例函数解决实际问题。
二. 学情分析九年级的学生已经学习了函数的基本概念和性质,对函数有一定的认识和理解。
但是,对于反比例函数的理解可能还不够深入,需要通过本节课的学习来加深对反比例函数的理解。
同时,学生需要通过实例来理解反比例函数的实际应用。
三. 说教学目标1.知识与技能目标:学生能够掌握反比例函数的定义和性质,能够运用反比例函数解决实际问题。
2.过程与方法目标:学生通过自主学习和合作交流,培养解决问题的能力和团队协作能力。
3.情感态度与价值观目标:学生培养对数学的兴趣,提高学习的积极性和主动性。
四. 说教学重难点1.教学重点:反比例函数的定义、性质和解析式。
2.教学难点:反比例函数的实际应用和图象的理解。
五. 说教学方法与手段本节课采用自主学习、合作交流和实例分析的教学方法。
通过学生的自主学习,培养学生的独立思考能力;通过合作交流,促进学生之间的思维碰撞,提高团队协作能力;通过实例分析,让学生更好地理解反比例函数的实际应用。
六. 说教学过程1.导入:通过复习正比例函数和一次函数的知识,引导学生自然地过渡到反比例函数的学习。
2.新课导入:介绍反比例函数的定义和性质,让学生理解反比例函数的概念。
3.实例分析:通过实际问题,让学生运用反比例函数解决问题,加深对反比例函数的理解。
4.小组讨论:学生分组讨论反比例函数的性质和图象,培养学生的合作交流能力。
5.总结提升:教师引导学生总结反比例函数的知识,加深对反比例函数的理解。
6.课堂练习:学生进行课堂练习,巩固反比例函数的知识。
7.课后作业:布置相关的课后作业,让学生进一步巩固反比例函数的知识。


第二十六章反比例函数(九下)一、基础复习1. 反比例函数的概念定义:形如y=kx(k为常数,k≠0) 的函数称为反比例函数,其中x是自变量,y是x的函数,k是比例系数。
三种表达式方法:y=kx或xy=k 或y=kx-1 (k≠0).【注意】(1)k≠0;(2)自变量x≠0;(3)函数y≠02. 反比例函数的图像和性质(1)反比例函数的图像:反比例函数y=kx(k≠0)的图像是双曲线__,它既是轴对称图形又是中心对称图形,反比例函数的两条对称轴为直线y = x__和y=-x__;对称中心是:原点(2) 反比例函数的性质(3) 反比例函数比例系数 k 的几何意义k 的几何意义:反比例函数图像上的点 (x,y) 具有两坐标之积 (xy=k) 为常数这一特点,即过双曲线上任意一点,向两坐标轴作垂线,两条垂线与坐标轴所围成的矩形的面积为|k|。
.规律:过双曲线上任意一点,向两坐标轴作垂线,一条垂线与坐标轴、原点所围成的三角形的面积为|k|2。
3. 反比例函数的应用◑利用待定系数法确定反比例函数①根据两变量之间的反比例关系,设y=kx;②代入图像上一个点的坐标,即x、y 的一组对应值,求出k 的值;③写出解析式。
◑反比例函数与一次函数的图象的交点求直线y=k1x+b (k1≠0)和双曲线y=k2x(k2≠0)的交点坐标就是解这两个函数解析式组成的方程组。
◑利用反比例函数相关知识解决实际问题过程:分析实际情境→建立函数模型→明确数学问题。
注意:实际问题中的两个变量往往都只能取非负值。
二、常见考点考点一反比例函数的概念例1 下列函数中哪些是正比例函数?哪些是反比例函数?① y=3x-1 ② y=2x2③ y= 1x ④ y= 2x⑤ y=3x ⑥ y=- 1x ⑦ y= 13x⑧ y= 32x考点二反比例函数的图像和性质例2已知点A(1,y1),B(2,y2),C(-3,y3) 都在反比例函数 y=6x的图像上,则y1,y2,y3的大小关系是()A. y3<y1<y2B. y1<y2<y3C. y2<y1<y3D. y3<y2<y1解析:方法①分别把各点代入反比例函数求出y1、y2、y3的值,再比较出其大小即可.方法②:根据反比例函数的图像和性质比较。
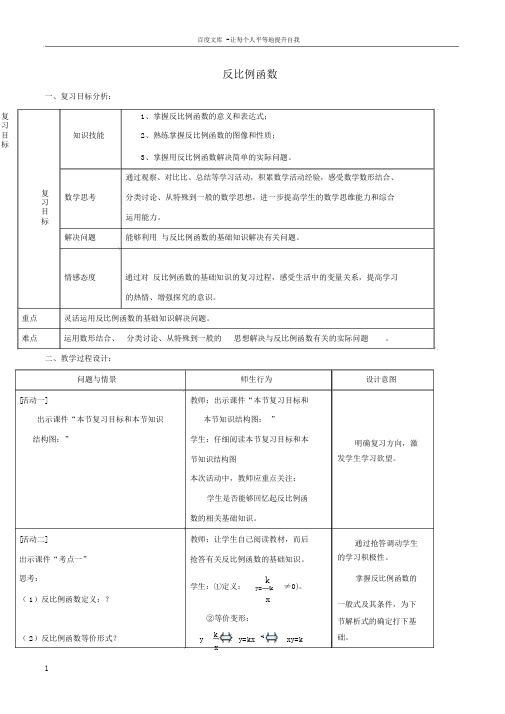
百度文库 - 让每个人平等地提升自我反比例函数一、复习目标分析:复1、掌握反比例函数的意义和表达式;习目知识技能2、熟练掌握反比例函数的图像和性质;标3、掌握用反比例函数解决简单的实际问题。
通过观察、对比比、总结等学习活动,积累数学活动经验,感受数学数形结合、复数学思考分类讨论、从特殊到一般的数学思想,进一步提高学生的数学思维能力和综合习目运用能力。
标解决问题能够利用与反比例函数的基础知识解决有关问题。
情感态度通过对反比例函数的基础知识的复习过程,感受生活中的变量关系,提高学习的热情、增强探究的意识。
重点灵活运用反比例函数的基础知识解决问题。
难点运用数形结合、分类讨论、从特殊到一般的思想解决与反比例函数有关的实际问题。
二、教学过程设计:问题与情景师生行为设计意图[活动一]教师:出示课件“本节复习目标和出示课件“本节复习目标和本节知识本节知识结构图:”结构图:”学生:仔细阅读本节复习目标和本节知识结构图本次活动中,教师应重点关注:学生是否能够回忆起反比例函数的相关基础知识。
[活动二]教师:让学生自己阅读教材,而后出示课件“考点一”抢答有关反比例函数的基础知识。
思考:k≠0)。
学生:①定义:y= (k( 1)反比例函数定义:?x②等价变形:( 2)反比例函数等价形式?y ky=kx-1xy=kx明确复习方向,激发学生学习欲望。
通过抢答调动学生的学习积极性。
掌握反比例函数的一般式及其条件,为下节解析式的确定打下基础。
百度文库 - 让每个人平等地提升自我y 与 x 成反比例通过等价变形,使学生真正掌握反比例函数的实质( 3)随堂训练:下列函数 y 与 x 是反比例函数的是 ?③ y 与 x 是反比例函数的是③、⑥、通过随堂训练得知x -1⑧学生的掌握情况,为下①y5② y=kx教师:( 1)定义: y= k(k ≠ 0) 中 k面的学习做铺垫。
③ y= 1④ y=2x⑤ x y=0x通过让学生解释② y=kx3≠0 原因?x ⑥ y=-x -1⑦ 2y=x⑧ y=3( 2)第⑤个 x y=0为何不是反比例⑤ x y=0 为何不是反比例2x函数?函数进一步强调反比例学生:解释② y= k⑤ x y=0函数的定义,从而掌握x知识的本质。
广西南宁市四十九中九年级数学《反比例函数的小结与思考》复习讲学稿内容:反比例函数 课型:复习 学习目标:1.了解反比例函数的意义.2.会根据已知条件确定反比例函数表达式、画反比例函数的图像、用反比例函数解决某些实际问题.一、基本知识回顾. 1.已知反比例函数ky x=的图象经过点(36)A --,,则这个反比例函数的解析式是 .2.近视眼镜的度数y (度)与镜片焦距x (米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y 与镜片焦距x 之间的函数关系式为 . 3.在反比例函数3k y x-=图象的每一支曲线上,y 都随x 的增大而减小,则k 的取值范围是 ( )A .k >3B .k >0C .k <3D . k <04. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m 3) 的反比例函数,其图象如图1所示.当气球内的气压大于120 kPa 时,气球将爆炸.为了安全起见,气球的体积应( )A .不小于54m 3B .小于54m 3C .不小于45m 3D .小于45m 35. 过反比例函数(0)ky k x=>的图象上的一点分别作x 、y 轴的垂线段,如果垂线段与x 、y 轴所围成的矩形面积是6,那么该函数的表达式是______;若点A(-3,m)在这个反比例函数的图象上,则m=______.6、如果点(3,-4)在反比例函数ky x=的图象上,那么下列各点中,在此图象上的是 A.(3,4) B. (-2,-6) C.(-2,6) D.(-3,-4)二、例题精讲例1 某汽车的功率P 为一定值,汽车行驶时的速度v (米/秒)与它所受的牵引力F (牛)之间的函数关系如右图所示:(1)这辆汽车的功率是多少?请写出这一函数的表达式;_4(2)当它所受牵引力为1200牛时,汽车的速度为多少千米/时? (3)如果限定汽车的速度不超过30米/秒,则F 在什么范围内?例2 如图,已知反比例函数xk y 1=的图象与一次函数b x k y +=2的图象交于A 、B 两点,)2,1(),,2(--B n A .(1)求反比例函数和一次函数的关系式; (2)在直线AB 上是否存在一点P ,使APO ∆∽AOB ∆,若存在,求P 点坐标;若不存在,请说明理由.例3、 探索应用:如图2,已知(30)A -,,(04)B -,为双曲线(0)y x x =>上的任意一点,过点P 作PC x ⊥轴于点C ,PO y ⊥轴于点D .求四边形ABCD 面积的最小值,并说明此时四边形ABCD 的形状.三、学习体会第26题图21-1y OxP1.本节课你有哪些收获?2.你认为老师上课过程中还有哪些须要注意或改进的地方?四、巩固提升1.已知点(12)-,在反比例函数ky x=的 图象上,则k = .2.在对物体做功一定的情况下,力F (牛)与此物体在力的方向上移动的距离s (米)成反比例函数关系,其图象如图所示,P (5,1)在图象上,则当力达到10牛时,物体在力的方向上移动的距离是 米. 3. 已知反比例函数的图象经过点(m ,2)和(-2,3),则m 的值为 .4.若正方形AOBC 的边OA 、OB 在坐标轴上,顶点C 在第一象限且在反比例函数y =x1的图像上,则点C 的坐标是 .5. 如图,某个反比例函数的图象经过点P, 则它的解析式为( )A.y =1x (x>0) B.y =-1x (x>0) C.y =1x (x<0) D.y =-1x(x<0) 6.对于反比例函数2y x=,下列说法不正确...的是( ) A .点(21)--,在它的图象上 B .它的图象在第一、三象限C .当0x >时,y 随x 的增大而增大D .当0x <时,y 随x 的增大而减小7.反比例函数6y x=-的图象位于( ) A .第一、三象限 B .第二、四象限 C .第二、三象限 D .第一、二象限 8.某空调厂装配车间原计划用2个月时间(每月以30天计算),每天组装150台空调. (1)从组装空调开始,每天组装的台数m (单位: 台/天)与生产的时间t (单位:天)之间有怎样的函数关系?(2)由于气温提前升高、厂家决定这批空调提前十天上市,那么装配车间每天至少要组装多少空调? 9.如图,已知A(-4,2)、B(n ,-4)是一次函数y kx b =+的图象与反比例函数my x=的图象的两个交点.(1) 求此反比例函数和一次函数的解析式;(2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.10、已知双曲线kyx=与直线14y x=相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线kyx=上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线kyx=于点E,交BD于点C.(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.(第10题)。
【反比例函数复习与小结】《反比例函数:小结与思考》教学设计【反比例函数复习与小结】《反比例函数:小结与思考》教学设计作为一名教职工,可能需要进行教学设计编写工作,教学设计是把教学原理转化为教学材料和教学活动的计划。
我们应该怎么写教学设计呢?以下是小编收集整理的【反比例函数复习与小结】《反比例函数:小结与思考》教学设计,欢迎大家分享。
[教学目标]1.回顾反比例函数的概念.通过实际问题,进一步感受用反比例函数解决实际问题的过程与方法,体会反比例函数是分析、解决实际问题的一种有效的模型.2.归纳总结反比例函数的图象和性质,进一步体会形数结合的.数学思想方法.[教学过程]1.回顾、梳理本章的知识:如同已经学过的有关方程、函数的内容一样,本章内容分为3块:(1)从生活到数学:从问题到反比例函数,即建构实际问题的数学模型;(2)数学研究:反比例函数的图象与性质;(3)用数学解决问题:反比例函数的应用.2.可以设计一组问题,重点归纳、整理反比例函数的图象与性质,进一步感受形数结合的数学思想方法.例如:(1)由形到数——用待定系数法求反比例函数的关系式;由图象的位置或图象的部分确定函数的特征;(2)由数到形――根据反比例函数关系式或反比例函数的性质,确定图形的位置、趋势等;(3)形数结合——函数的图象与性质的综合应用2例如:如图,点P是反比例函数y?上的一点,PD垂直x轴于点D,则△xPOD的面积为________3.设计一个实际问题,让学生经历“问题情境一建立模型一求解一解释与应用”的基本过程.例如:为了预防“非典”,某学校对教室采用药薰法进行消毒.已知药物燃烧时.室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例(如图).现测得药物8min燃毕,此时室内空气中每立方米含药量为6mg。
(1)写出药物燃烧前、后y与x的函数关系式;(2)研究表明,当空气中每立方米的含药量低于1。
反比例函数知识点知识点总结反比例函数知识点总结一、反比例函数的定义一般地,如果两个变量 x、y 之间的关系可以表示成 y = k/x(k 为常数,k≠0)的形式,那么称 y 是 x 的反比例函数。
其中,x 是自变量,y 是因变量。
因为 x 在分母上,所以自变量 x 的取值范围是x≠0。
例如,y = 3/x,y =-5/x 等都是反比例函数。
二、反比例函数的表达式反比例函数常见的表达式有以下三种形式:1、 y = k/x(k 为常数,k≠0)2、 xy = k(k 为常数,k≠0)3、 y = kx^(-1)(k 为常数,k≠0)这三种形式在本质上是相同的,只是形式上有所不同,我们可以根据具体的题目条件灵活选择使用。
三、反比例函数的图象反比例函数的图象是双曲线。
当 k>0 时,双曲线的两支分别位于第一、三象限,在每一象限内 y 随 x 的增大而减小;当 k<0 时,双曲线的两支分别位于第二、四象限,在每一象限内 y 随 x 的增大而增大。
需要注意的是,反比例函数的图象永远不会与坐标轴相交,因为自变量x≠0,函数值y≠0。
四、反比例函数图象的性质1、对称性反比例函数的图象既是轴对称图形,又是中心对称图形。
对称轴有两条,分别是直线 y = x 和直线 y = x。
对称中心是坐标原点(0,0)。
2、增减性在每个象限内,当 k>0 时,y 随 x 的增大而减小;当 k<0 时,y 随 x 的增大而增大。
3、渐近线双曲线无限接近于 x 轴和 y 轴,但永远不会与它们相交。
五、反比例函数中 k 的几何意义1、过反比例函数 y = k/x(k≠0)图象上任意一点 P 作 x 轴、y 轴的垂线 PM、PN,垂足为 M、N,则矩形 PMON 的面积 S = PM·PN =|y|·|x| =|xy| =|k|。
2、三角形面积若连接 PO,则三角形 POM 的面积 S = 1/2 |k| 。
六、反比例函数与一次函数的综合应用1、求交点坐标联立反比例函数和一次函数的解析式,组成方程组,解方程组即可得到交点坐标。