江苏省昆山市锦溪中学七年级数学上册 第五章 第4课时 图形的变化课时检测 苏科版

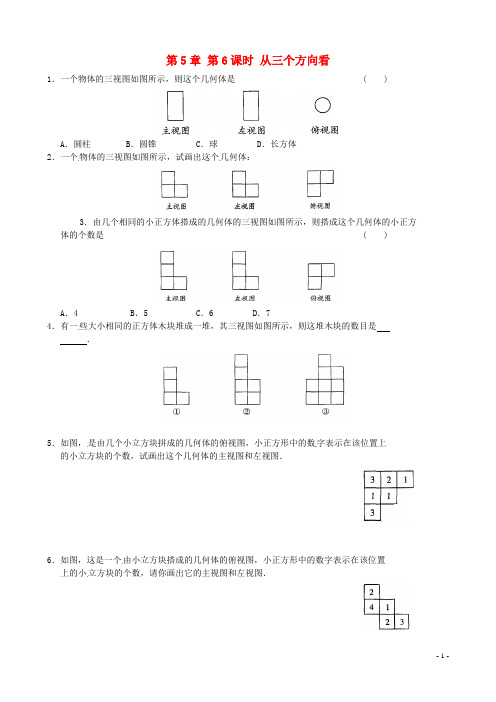
第5章第6课时从三个方向看
1．一个物体的三视图如图所示，则这个几何体是 ( )
A．圆柱 B．圆锥 C．球 D．长方体
2．一个物体的三视图如图所示，试画出这个几何体：
3．由几个相同的小正方体搭成的几何体的三视图如图所示，则搭成这个几何体的小正方体的个数是 ( )
A．4 B．5 C．6 D．7
4．有一些大小相同的正方体木块堆成一堆，其三视图如图所示，则这堆木块的数目是．
5．如图，是由几个小立方块拼成的几何体的俯视图，小正方形中的数字表示在该位置上的小立方块的个数，试画出这个几何体的主视图和左视图．
6．如图，这是一个由小立方块搭成的几何体的俯视图，小正方形中的数字表示在该位置上的小立方块的个数，请你画出它的主视图和左视图．
7．如图所示的两幅图分别是由几个小立方块所搭几何体的左视图，小正方形中的数字表示在该位置上的小立方块的个数，请画出相应的几何体的主视图和俯视图．
8．用小立方块搭一个几何体，使得它的主视图和俯视图如图所示，这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
答案
1．A 2．略 3．B 4．11 5—7．略
8．最少需要10个小立方块，最多需要16个小立方块。

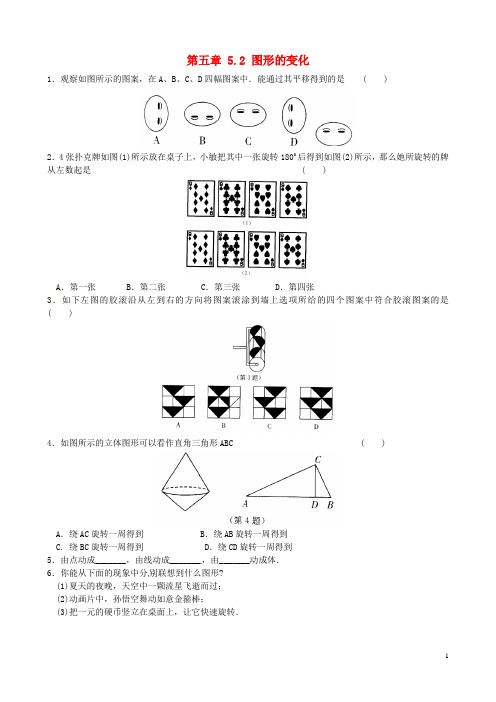
第五章 5.2 图形的变化1．观察如图所示的图案，在A、B、C、D四幅图案中．能通过其平移得到的是 ( )2．4张扑克牌如图(1)所示放在桌子上，小敏把其中一张旋转1800后得到如图(2)所示，那么她所旋转的牌从左数起是 ( )A．第一张 B．第二张 C．第三张 D．第四张3．如下左图的胶滚沿从左到右的方向将图案滚涂到墙上选项所给的四个图案中符合胶滚图案的是( )4．如图所示的立体图形可以看作直角三角形ABC ( )A．绕AC旋转一周得到 B．绕AB旋转一周得到C. 绕BC旋转一周得到 D．绕CD旋转一周得到5．由点动成_______，由线动成_______，由_______动成体．6．你能从下面的现象中分别联想到什么图形?(1)夏天的夜晚，天空中一颗流星飞逝而过；(2)动画片中，孙悟空舞动如意金箍棒；(3)把一元的硬币竖立在桌面上，让它快速旋转．7．如图所示第一行的图形绕虚线旋转一周，便能形成第二行的某个几何体，用线连一连．8．图形的翻折是指图形沿着某条直线折叠，能够与另一个图形重合，实际上，有好多的图形本身就具备这个特征，即这个图形沿着某条直线折叠，能与它本身重合，例如如图(1)所示就是这样的图形，我们可以找出其中直线如MN．观察图(2)～(5)中的图形，哪些图具有这样的特征?你能找出其中的直线吗?把它画出来．9．右边的图案是由下面五种基本图中的两种拼接而成，这两种基本图形是 ( )A．①⑤ B．②④ C．③⑤ D．②⑤10．如图，将三角尺ABC(其中∠ABC=600，∠C=900)绕点B按顺时针转动一个角度到A1B1C1的位置，使得点A、B、C1在同一条直线上，那么这个角度等于 ( )A. 1200 B．900 C．600 D．30011．如图△ABC是等腰直角三角形，BC是斜边，P为△ABC内一点，将△ABP绕点A逆时针旋转后与△ACP’重合,如果AP=3，那么线段PP’的长等于_______．12．如图，在正方形网格中，以点A为旋转中心,将△ABC按逆时针方向旋转900，画出旋转后的△AB1C1．13．剪纸是中国的民间艺术，扬州剪纸更是闻名于世．郭沫若曾亲笔题诗：“扬州艺人张永寿，剪出百花齐放来．请看剪下春秋，顿使东风遍九垓．”如图(1)所示是一个剪纸的过程，你能按照以下的步骤试着剪一个吗?你知道，剪纸艺术的数学原理吗?你能否判断图(2)中的哪些图可以由剪纸剪出来，哪些不能，并说理理由．14．(1)如图所示的是北京2008年奥运会的会标，最下面的是奥运五环标志．你能说出它是怎样形成的吗?(不虑五环的颜色)(2)你能说出下面的图案是怎样形成的吗?(不考虑颜色)15．如图，在甲组图形中，每个图形是由4种简单图形A、B、C、D中的某两个图形组合而成的．例如：由A、B组成的图形记为A*B；在乙组图形中的(a)，(6)，(c)，(d)4个图中．表示“A*D”和“A*C”的是( )A. (a)(b) B．(b)(c) C．(c)(d) D．(b)(d)16．如下图是一组人物图画，现已经画出了8幅，请你通过观察画出所缺的那一幅图案．17．认真观察图(1)的4个图中阴影部分构成的图案．回答下列问题：(1)请写出这四个图案都具有的两个共同特征。

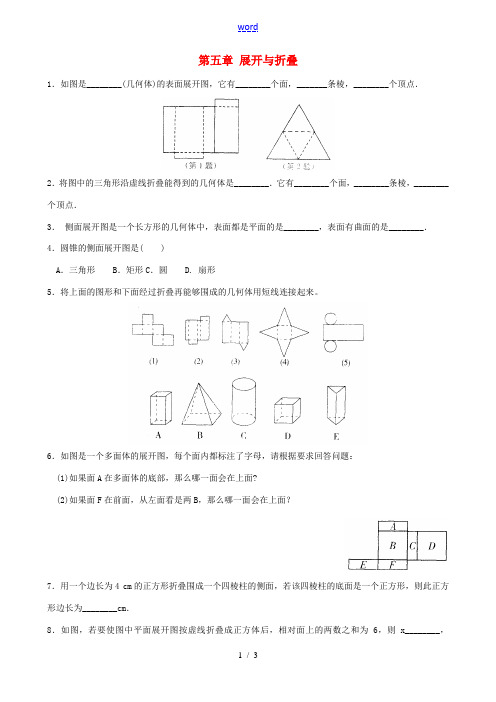
第五章展开与折叠1．如图是________(几何体)的表面展开图，它有________个面，_______条棱，________个顶点．2．将图中的三角形沿虚线折叠能得到的几何体是________．它有________个面，________条棱，________个顶点．3．侧面展开图是一个长方形的几何体中，表面都是平面的是________，表面有曲面的是________．4．圆锥的侧面展开图是( )A．三角形 B．矩形C．圆 D. 扇形5．将上面的图形和下面经过折叠再能够围成的几何体用短线连接起来。

6．如图是一个多面体的展开图，每个面内都标注了字母，请根据要求回答问题：(1)如果面A在多面体的底部，那么哪一面会在上面?(2)如果面F在前面，从左面看是两B，那么哪一面会在上面？7．用一个边长为4 cm的正方形折叠围成一个四棱柱的侧面，若该四棱柱的底面是一个正方形，则此正方形边长为________cm．8．如图，若要使图中平面展开图按虚线折叠成正方体后，相对面上的两数之和为6，则x________，y________．9．如图是一个正方体纸盒的展开图，在其中的四个正方形内标有数字1，2，3和-3．若要在其余正方形内分别填上-1，-2，使得按虚线折成正方体后，相对面上的两数互为相反数，则A处应填________，B 处应填________．10．将一个五棱柱沿一些棱剪开后展开成一个平面图形．至少要剪开多少条棱？11．有下列四句话：①棱拄的棱数一定是三的倍数：②棱锥的棱数一定是偶数：③有一个棱柱的棱数减去面数等于5：④棱锥的顶点数等于面数．说法正确的有________句，它们的序号是________．12．将一个正方体沿某些棱展开后．能够得到的平面图形是( )13．一个正方体的平面展开图如图所示，将它折成正方体后“建”字对面是( )A．和B．谐C．凉D．山参考答案1．长方体6 12 82．三棱锥 4 6 43．棱柱圆柱4．D5．(1)-D (2)-A (3)-E (4)-B (5)-C6．(1)F(2)C或E7． 18． 5 39．-2 -110．表面展开图由两个五边形和五个长方形相接而组成，最少有18条边．每两条边由一条棱剪出，至少要剪9条棱．11．3①②④12. C13. D。

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！课时练5.4《主视图、左视图、俯视图》一、选择题1.下列几何体中，三视图完全相同的是（）A.正方体B.圆柱体C.圆锥体D.五棱柱2.图中为某几何体的分别从上面、前面、左边看到的三个图形，该几何体是（）A.圆锥B.圆柱C.正三棱柱D.正三棱锥3.下列几何体中，从左面看到的图形是圆的是（）A.B.C.D.4.如图是由4个完全相同的正方体搭成的几何体，则（）A.从正面看、左面看和从上面看得到的图形都相同B.从上面看和从左面看得到的图形相同C.从正面看和从上面看得到的图形相同D.从正面看和从左面看得到的图形相同5.由6个大小相同的正方体搭成的几何体如图所示，比较从三个不同方向看到的平面图形的面积，则（）A.从三个不同方向看到的平面图形的面积一样大B.从正面看到的平面图形面积最小C.从左面看到的平面图形的面积最小第2题第4题D.从上面看到的平面图形的面积最小6.图中的三视图所对应的几何体是（）A. B.C.D.7.一个几何体由大小相同的小立方块搭成，从上面看到的几何体的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到的这个几何体的形状图是（）A.B.C.D.8.一个小正方体的六个面分别标有数字1、2、3、4、5、6，从不同方向看到的情形如图，1、2、5对面的数字分别是（）A.3、4、6B.3、6、4C.4、6、3D.6、4、39.如图，是按照比例尺为1：10绘制的一个几何体的三视图（单位：cm），则该几何体的侧面积是（）A.4900c B.7000c C.8400c D.10500c第5题第6题第7题第8题二、填空题10.在如图所示的几何体中，主视图、左视图和俯视图完全相同的几何体是_____．（写出所有正确答案的序号）11.下列几何体中，主视图是三角形的是_____．12.一个立体图形如图，从_____面看到的形状是，从_____面看到的形状是，从_____面看到的形状是．13.若干个桶装方便面摆放在桌子上，小明从三个不同方向看到的图形（分别是：主视图，左视图，和俯视图）如图所示，则这一堆方便面共有_____个．14.一个几何体由若干个相同的正方体组成，其主视图和俯视图如图所示，则这个几何体中正方体的个数最少是_____个，最多是_____个．15.几个完全相同的小正方体搭成如图的几何体，从上面拿掉一个或者几个小正方体（不能直接拿掉被压在下面的小正方体）而不改变几何体的三视图的方法有_____种．第9题第10题第11题16.如图，是一个几何体从三个不同方向看到的平面图形，则这个几何体的侧面积是_____（结果保留π）．17.如图，由十个小正方体组成的几何体中，若每个小正方体的棱长都是2，则该几何体的主视图和左视图的面积之和是_____．三、解答题18.如图，是由10个同样大小的小正方体搭成的物体．（1）请在网格中分别画出从正面、上面观察该几何体得到的平面图形并涂上阴影；（2）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体从正面和上面观察得到的平面图形不变，你认为最多还可以添加_____个小正方体．19.用小立方块搭一个几何体，使它的主视图和俯视图如图所示，俯视图中小正方形中字母表示该位置小立方块的个数，请解答下列问题：（1）a=_____，b=_____，c=_____．（2）这个几何体最少由_____个小立方块搭成，最多由_____个小立方块搭成．第13题第14题第15题第16题第17题（3）当d=e=1，f=2时，画出这个几何体的左视图．20.如图，是从上面看到的由几个小正方体搭成的几何体的图形，小正方形上的数字表示在该位置上小正方体的个数．回答下列问题：（1）从正面、左面观察该几何体，分别画出你所看到的图形；（2）该几何体的表面积是_____．21.如图是分别从正面、左面、上面观察一个几何体得到的图形，请解答以下问题：（1）这个几何体的名称为_____；（2）若从正面看到的是长方形，其长为10cm；从上面看到的是等边三角形，其边长为4cm，求这个几何体的侧面积．参考答案1、A2、C3、D4、D5、C6、B7、C8、A9、C10、①③11、②③12、正；上；左13、有2+2+1=5（个）14、5；615、416侧面积为：π×2×4=8π（cm2）．17、2×2×（6+6）=4818、19、20、21、。

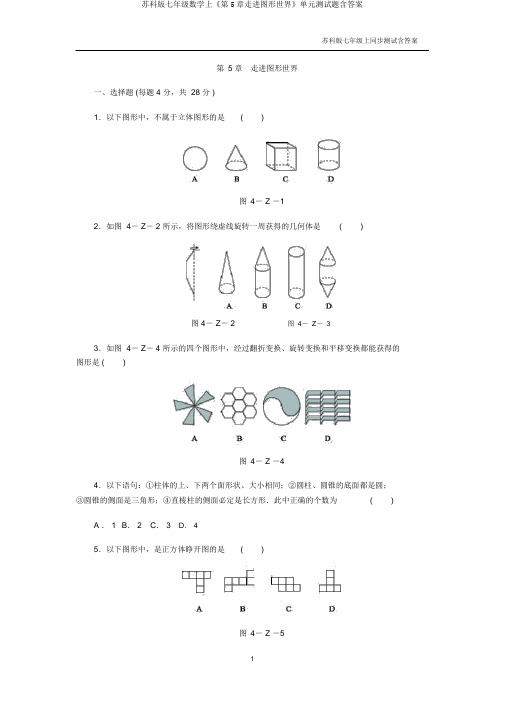
苏科版七年级上同步测试含答案第5 章走进图形世界一、选择题 (每题 4 分，共 28 分 )1．以下图形中，不属于立体图形的是()图4－ Z －12．如图 4－ Z－ 2 所示，将图形绕虚线旋转一周获得的几何体是()图 4－ Z－ 2图4－Z－33．如图 4－ Z－ 4 所示的四个图形中，经过翻折变换、旋转变换和平移变换都能获得的图形是 ()图4－ Z －44．以下语句：①柱体的上、下两个面形状、大小相同；②圆柱、圆锥的底面都是圆；③圆锥的侧面是三角形；④直棱柱的侧面必定是长方形．此中正确的个数为()A ． 1 B． 2 C． 3D． 45．以下图形中，是正方体睁开图的是()图4－ Z －56．用一个平面去截一个几何体，获得的截面是圆，这个几何体可能是()A ．圆锥B．圆柱C．球体D． A ， B， C 都有可能7．一个几何体的三视图如图4－ Z－ 6 所示，则这个几何体是()A ．三棱锥B ．三棱柱C．圆柱 D ．长方体二、填空题 (每题 4 分，共 24 分 )8．三棱锥是由________个面围成的，有________个极点，有 ________条棱．图4－ Z －69．如图 4－ Z－ 7 所示的几何体有________个面，面面订交成________线．图 4－ Z －710.如图 4－Z － 8 所示是一个由 6 个大小相同、棱长为 1 的小正方体搭成的几何体，那么它的俯视图的面积是________．图 4－ Z－ 811．如图 4－ Z － 9，②是①中图形的________视图．图 4－ Z －912．一个正方体的每个面上都有一个汉字，其表面睁开图如图4－ Z－ 10 所示，那么在该正方体中和“毒”字相对的字是________．图 4－ Z －1013．如图 4－ Z －11 是一块从一个边长为50 cm 的正方形资猜中剪出的垫片，现测得FG ＝5 cm，则这个剪出的垫片的周长是________cm.图4－Z － 11三、解答题 (共 48 分)14． (8 分) 将第一行的图形绕轴旋转一周，便获得第二行的几何体，用线连一连．图4－ Z －1215．(8 分 )如图 4－ Z－ 13 是一个小正方体所搭几何体从上边看获得的平面图形，正方形中的数字表示该地点处小正方体的个数，请你画出它从正面和从左面看获得的平面图形．图4－ Z －1316． (10 分)如图 4－ Z－ 14 所示的是某个几何体的三视图．(1)说出这个立体图形的名称；(2)依据图中的相关数据，求这个几何体的表面积．图4－ Z －1417． (10 分)察看图 4－ Z－ 15，回答以下问题：(1)甲、乙两图分别能折成什么几何体？简述它们的特点；(2)设几何体的面数为 F，极点数为 V，棱数为 E，请计算 (1) 中两个几何体的 F ＋ V－ E 的值．图4－ Z －1518． (12 分)用相同大小的正方体木块结构一个模型(不停开 )，如图4－ Z－16 分别是其主视图和左视图，结构这样的模型，最多需要几块木块？最少需要几块？并画出相应的俯视图．图4－ Z －161． A 2． D 3． B4．C5 ． B6． D 7． B 8．4 469． 3曲10． 511．主12．防13． 21014．解： A 旋转后获得图形 c，B 旋转后获得图形 d，C 旋转后获得图形 a，D 旋转后获得图形e， E 旋转后获得图形 b.15．解：如下图：16．解： (1) 这个立体图形是直三棱柱．(2)表面积为12× 3× 4× 2＋ 15× 3＋15× 4＋15× 5＝ 192.17．解： (1)甲、乙两图能折成的几何体分别是长方体(四棱柱 )与四棱锥．长方体由 6 个面围成，此中有 2 个大小相同的底面，侧面都是长方形且侧棱长相等，四棱锥由 5 个面围成，它只有 1 个底面，侧面都是三角形．(2)长方体有 6 个面， 8 个极点， 12 条棱，所以 F ＋ V－ E＝ 2；四棱锥有 5 个面， 5 个极点，8 条棱，所以 F＋ V－E＝ 2.18．解：依据该模型的主视图、左视图，在脑筋中想象它的三维形状：共有两层，基层起码需 5 块，至多需16 块；上层起码需 2 块，至多需 4 块．所以，该模型最少需7 块，最多需 20 块．俯视图如下图，此中暗影部分表示此处有两层小木块．。

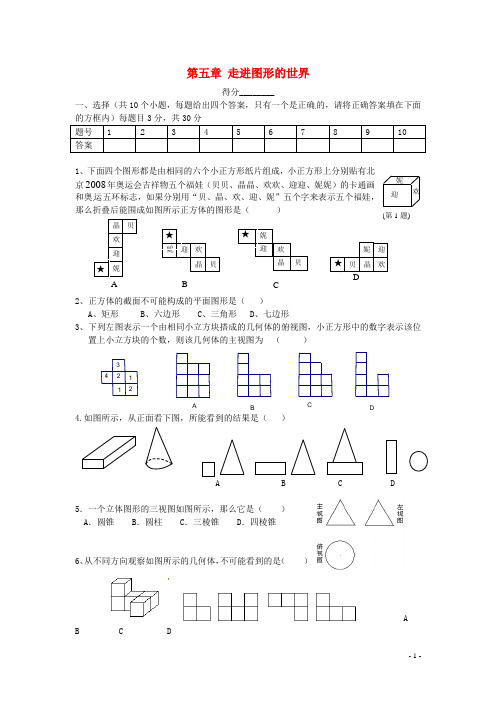
第五章 走进图形的世界得分________一、选择（共10个小题，每题给出四个答案，只有一个是正确的，请将正确答案填在下面的方框内）每题目3分，共30分 题号 1 2 3 4 5 6 7 8 9 10 答案1、下面四个图形都是由相同的六个小正方形纸片组成，小正方形上分别贴有北京2008年奥运会吉祥物五个福娃（贝贝、晶晶、欢欢、迎迎、妮妮）的卡通画和奥运五环标志，如果分别用“贝、晶、欢、迎、妮”五个字来表示五个福娃，那么折叠后能围成如图所示正方体的图形是（ ）2、正方体的截面不可能构成的平面图形是（ ）A 、矩形B 、六边形C 、三角形D 、七边形3、下列左图表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，则该几何体的主视图为 （ ）4.如图所示，从正面看下图，所能看到的结果是（ ）A B C D5．一个立体图形的三视图如图所示，那么它是（ ） A ．圆锥 B ．圆柱 C ．三棱锥 D ．四棱锥 6、从不同方向观察如图所示的几何体，不可能看到的是（ ）AB C D224113A BC D C 迎 妮 欢 晶 贝 D ★（B 妮 迎 欢 晶 贝 ★（晶 欢迎妮 贝A ★欢晶 妮 迎 ★（贝 欢迎 妮(第1题)第4题 C BAD 第3题7、下列各物体中，是一样的为（ ）A ．（1）与（2）B ．（1）与（3）C ．（1）与（4）D ．（2）与（3） 8．将如图所示的正方体沿某些棱展开后，能得到的图形是（ ）★★★★A ．B ．C ．D ．9．下图中几何体的左视图为（ ）10、若干个正方体形状的积木摆成如图所示的塔形，平放于桌面上，上面 正方体的下底四个顶点是下面相邻正方体的上底各边中点，最下面的正方体 棱长为1，如果塔形露在外面的面积超过7，则正方体的个数至少是（ ）A 、2B 、3C 、4D 、5（8至10为选做题，即拔高题，难度应大一些） 二、填空（共6个小题，每题3分，共18分）1看风景，若一个实物正面看是三角形，侧面看也是三角形，上面看是圆，这个实物是 体。

图形的变化预学目标1．通过课本中的“想一想”感受“点动成线、线动成面、面动成体”．2．通过课本中的“做一做”感受“平移”、“旋转”、“翻折”这三种平面图形的变换方式．3．欣赏课本中的美丽图案，尝试分析图案的形成过程．知识梳理1．平面图形的平移（如图1）把一个平面图形按指定的方向平移到另一个位置，这种图形变换称为_______．说明：(1)平面图形的平移改变了图形的_______，不改变图形的_______和_______．(2)平面图形的平移是图形的整体运动，所以图形中的每个点都按相同的_______移动了相等的_______．2．平面图形的旋转（如图2）把一个平面图形绕它所在平面内的一个点（或一条直线）旋转到另一个位置，通常我们将这种图形变换称为_______．说明：(1)平面图形的旋转改变了图形的_______，不改变图形的_______和_______．(2)如果将一个平面图形绕某一条直线旋转一周，那么它所经过的区域形成了一个_______．3．平面图形的翻折（如图3）平面图形翻折的实质：把一个平面图形绕某一_______旋转_______°到另一个位置．说明：(1)平面图形的翻折改变了图形的_______，不改变图形的_______和_______．(2)翻折后的图形与翻折前的图形形成了我们在小学阶段就已经认知的_______图形．例题精讲例1一个几何体可以由平面图形旋转而成．如图，第一行的图形绕虚线旋转一周，便能形成第二行的某个几何体，请你用线连一连．提示：从三角形、长方形、圆等几何图形的基本特征入手，根据面动成体的特征和生活常识求解．解答：①－C；②－D；③－E；④－B；⑤－A．点评：面动成体，关键是运动，从运动的观点看事物容易解决问题．例2观察下列图形，你能说出下列图案是怎样形成的吗？提示：本题中体现了图形的三种变化：平移、旋转、翻折．解答：图①是由一个基本图形经旋转形成的；图②是由一个基本图形经旋转形成的；图③是由一个基本图形经平移形成的．点评：分解图形，掌握三种图形变换方式的运动特征是解题的关键．热身练习1．下列各组图形中，分别将第一个图形作怎样的变化，就可以与第二个图形重合？____________________________2．下列现象中，属于平移的是( )A．将一张纸沿它的中线折叠B．飞碟的快速转动C．电梯的上下移动D．翻开书中的每一页纸张3．矩形绕其一边旋转一周形成的几何体叫_______，直角三角形绕其中一条直角边旋转一周形成的几何体叫_______．4．如图所示的立体图形可以看做是Rt△ABC ( )A．绕AC旋转一周得到的B．绕AB旋转一周得到的C．绕BC旋转一周得到的D．绕CD旋转一周得到的5．将下图中的小船向左平移4格．6．在规格为6×6的正方形网格中，有一个L形图案（图中的阴影部分）．请你用三种不同的方法分别在下图中再给一个空白的小正方形并涂上阴影，使整个阴影部分成轴对称图形．7．请你来设计：现有如图所示的6种瓷砖，请用其中的四种（可以有相同的）设计图案．例如：先拼成图①，然后再通过对它的平移、旋转或翻折，设计出更美丽、更大型的图案，如图②、图③．你的设计是：（请画在下图中）先拼成：再变换、放大得：参考答案1．平移翻折旋转翻折2．C3．圆柱圆锥4．B 5．略6．略7．略。

第3课时图形的变化
1．长方形纸板绕它的一条边旋转一周后，形成的几何体是___________．
2．直角三角尺绕它的一条直角边旋转一周后，形成的几何体是__________．
3．一个半圆绕它的直径旋转一周后，形成的几何体是___________．
4．下列图案中，能通过如图所示的图案平移得到的是 ( )
5．观察如图所示的图案，说说它们分别是怎样形成的．
6．如图，虚线左边的图形绕虚线旋转一周，形成的几何体是 ( )
7．小明用如图所示的胶滚按从左到右的方向将图案滚涂到墙上，下列所给的四幅图案中，符合胶滚涂出的图案的是 ( )
8．如图，在方格纸中，△ABC向右平移_________格后得到△A＇B＇C＇．
9．如图，第一行中的每个图形绕虚线轴转1周后，能形成第二行中的某个几何体，请用线将对应的两个
连接起来．
10．如图，将方格中的阴影图形绕点Ｏ，按顺时针方向依次旋转90ｏ，会得到什么图形?请在图中画出．
11．如图，两个三角形的大小和形状是完全相同的．则下列情况下，各作什么变化可以使两个三角形完全重合?
12．如图，分析每个图形的形成过程．
参考答案
1．圆柱
2．圆锥
3．球
4．C
5．略
6．C
7．C
8．4
9．略
10．如图所示
11．①平移②翻折③旋转12．略。

苏教版初中七年级数学试题数学学科第五章第2节5.2《图形的运动》学讲预案一、自主先学1．点动成，线动成，面动成，旋转可以形成新的图形．2.长方形纸板、直角三角板、1元硬币经过旋转后形成的几何体分别为，， .3．下侧图形绕轴线旋转1周，能形成怎样的几何体？二、合作助学4．在下面两行图形中，分别找出相互对应的图形，并用线连接.5.你还能举出生活中的“点动成线，线动成面，面动成体”吗？6.在点划线一旁空白的方格中画图，使点划线两旁的图形完全相同．7．（1）是由图“回”向右平移而成的，将准备好的纸片沿虚线剪开，（1）怎样改变图形的位置可以得到图（2），你还能得到什么样的图案？（2）如果虚线以下的部分向右平移4格，得到怎样的图形？三、拓展导学8．将两个相同的直角三角尺相等的一边拼在一起，能拼出几种不同的图形，你能说出这些图形的名称吗？四、检测助学9. 右边各图形中，不是由翻折而形成的是（）10. 右边四个图形中，形成方法与另外三个不同的是（）11．你能说出右边的图案是怎样形成的吗？12．画出图案（1）沿虚线翻折后的图案．13．将图（2）绕着点A旋转1800，请你画出所得的图形．314．说一说右边图形的是如何由左边的图形变化来的.五、反思悟学15. 观察右边图形，你能说出它们是分别根据什么基本图形，经过怎样的变化形成的吗？习题试解预习法检验预习效果的最佳途径数学学科有别于其他学科的一大特点就是直接用数学知识解决问题。

因此,预习数学的关键是先看书,进而尝试做题。

学生经过自己的努力,初步理解和掌握了新的数学知识,还要通过做练习或解决简单的问题来检验自己预习的效果。

教材中每一小节后的思考练习题,是编者根据教学大纲的要求,对教材中要点和重点的概述,是对学生理解书本内容的具体评估。

因此,我们可以利用这些题目来检查自己的预习效果。

通过试解练习题,哪些知识点已知已会,哪些难懂不会,一下子就检验出来了。

对试解出来的习题,通过听课以加深理解;对试解不出来的习题,课堂上应格外4留心听讲,力求政克,为提高课堂学习质量打下坚实的基础。

第5章第2课时图形的变化
1．如图，将正方形图案绕点O旋转180°后，得到的图案是 ( )
2．如图，在5×5的方格纸中，将图①中的图形N平移后的位置如图②中所示，那么正确的平移方法是 ( )
A．先向下移动1格，再向左移动1格
B．先向下移动1格，再向左移动2格
C．先向下移动2格，再向左移动1格
D．先向下移动2格，再向左移动2格
3．如图，第二行的图形绕虚线旋转一周，便能形成第一行的某个几何体，用线连一连．
4．直角三角形的两条直角边分别为3 cm和4 cm，将这个直角三角形分别绕两条直角边
所在的直线旋转一周，所得几何体的体积分别是多少?(
1
3
V Sh
圆锥
)
5．如图，将阴影部分：
①向下平移3格；
②沿直线AB翻折；
③绕点A顺时针旋转90°．
分别画出上述变化后得到的图形．
6．用两个三角形、两个圆和两条平行线段设计一个图案，并给图案加上恰当的解说词．
7．如图所示，在五行五列的方格棋盘上放着一枚骰子，它和平常的骰子并不相同，它在棋盘上只能左、右、上、下运动，并且必须沿着它的棱翻动(也叫做滚着走)．开始时骰子在3C处，将骰子从3C处翻到3B处，骰子的形态如图①所示，再将骰子从3B处翻到2B处，骰子的形态如图②所示．
(1)继续将骰子从2B处翻到l B处，朝上的一面点数是多少?
(2)继续翻动骰子从1B处到1A处，朝上的一面点数是多少?
(3)如果将这枚骰子从图中原来的位置翻到5E的位置，则朝上的一面点数又是多少?
答案
1．D 2．C 3．略 4．16πcm3 12πcm3
5．略 6．略 7．(1)3 (2)5 (3)5。