当前位置：文档之家 › 流体力学第五章 管中流动 湍流-2

流体力学第五章 管中流动 湍流-2

  • 格式：pdf
  • 大小：1.67 MB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

李玉柱流体力学课后题答案 第五章

李玉柱流体力学课后题答案 第五章

第五章 层流、紊流及其能量损失5—1 (1)某水管的直径d ＝100 mm ，通过流量Q ＝4 L/s ，水温T ＝20℃；(2)条件与以上相同，但管道中流过的是重燃油，其运动粘度6215010m /s ν-=⨯。

试判别以上两种情况下的流态。

解：(1) 200C 时，水的运动粘性系数ν=1.007×10-6m 2/s ，24Q u d π=水的雷诺数Re 为：-3-6244 4 L/s 10Re 5060020001.00710m /s 3.140.1mud Q v v d π⨯⨯====>⨯⨯⨯，紊流 (2) 石油：-3-6244 4 L/s 10Re 339.7200015010m /s 3.140.1m ud Q v v d π⨯⨯====<⨯⨯⨯，层流 5—2 温度为0℃的空气，以4 m/s 的速度在直径为l00 mm 的圆管中流动，试确定其流态(空气的运动粘度为521.3710m /s ν-=⨯)。

若管中的流体换成运动粘度为621.79210m /s ν-=⨯的水，问水在管中呈何流态?解：空气的雷诺数Re 为：-524 m/s 0.1m Re 2919720001.3710m /sud v ⨯===>⨯，紊流 水的雷诺数Re 为：-624 m/s 0.1m Re 223 21420001.79210m /sud v ⨯===>⨯，紊流 5—3 (1)一梯形断面排水沟，底宽0.5m ，边坡系数cot θ＝1.5(θ为坡角)，水温为20℃，水深0.4m ，流速为0.1m ／s ，试判别其流态；(2)如果水温保持不变，流速减小到多大时变为层流?解：200C 时，水的运动粘性系数ν=1.007×10-6m 2/s 水力直径为(0.520.60.5)0.4/20.23m 0.50.722AR χ+⨯+⨯===+⨯ 4-620.1m/s 0.23m Re 2.24101.00710m /sR uR ν⨯===⨯⨯，42.24102000⨯>，湍流 水流为层流时Re 500uR ν≤=(明渠流)，故 63Re 500 1.00710 2.210m/s 0.23u R ν--⨯⨯≤==⨯ 5—4 由若干水管组装成的冷凝器，利用水流经过水管不断散热而起到冷凝作用。

流体力学中的流体流动的湍流流动的湍流层效应

流体力学中的流体流动的湍流流动的湍流层效应

流体力学中的流体流动的湍流流动的湍流层效应湍流是流体力学中一种非线性、不稳定的流动状态，其特征是流动速度和压力的瞬时波动，并且在时间和空间上都是随机的。

湍流流动在自然界广泛存在，涉及到气体、液体以及其他可流动的物质。

在流体力学中，研究湍流流动是一项重要的课题，其中湍流层效应是湍流流动的一个重要现象。

湍流层是指在管道、河流或者空气流动等情况中，流体与固体壁面发生相互作用时，由于摩擦力的存在，使得流体流动产生的一种特殊现象。

在湍流层中，流体速度在垂直于壁面的方向上出现快速变化，并且速度强度较大；而在水平方向上，速度呈现规则的变化。

这种非均匀性的流动导致了湍流层效应的出现。

湍流层效应对流体流动产生了许多重要影响。

首先，湍流层效应增强了流体的混合和传热能力。

由于湍流层的不断变化和混乱性，使得流体中的温度和组分更容易混合，并且能够更快地传递热量。

这在很多工程和自然现象中都显得尤为重要，比如在化工过程中的反应器设计、气候系统中的空气传热等。

其次，湍流层效应增加了流体的阻力。

在湍流层中，流体与壁面之间摩擦力的存在导致了阻力的增加。

这使得流体在流动过程中需要消耗更多的能量，进而降低了流体的速度。

在水动力学和风力学中，湍流层效应对于流体在管道、水流中的输送都会产生明显的影响。

此外，湍流层效应还与声传播有关。

在湍流层中，流速的不断变化和速度梯度的存在导致了空气的扰动和噪声的产生。

这对于一些对声音敏感的场合，比如飞机起降噪声减低、建筑物噪声控制等有着重要的实际意义。

总之，湍流层效应作为流体力学中湍流流动的一个重要现象，对于流体的混合与传热、流体的阻力以及声传播等方面都产生了重要的影响。

深入研究湍流层效应对于理解和控制湍流流动具有重要的意义，能为相关领域的工程和科学研究提供更多的参考和指导。

流体力学D课件 第五章

流体力学D课件 第五章
Re
hf
Vd
对数形式为
lg 1.806 lg Re
在尼古拉兹图中为一条斜直线。
(2) 过渡区 (2300 Re 4000) (3) 湍流完全光滑管区
情况复杂，无单一计算公式。
布拉修斯公式 (4000 Re 105 )
0.3164 Re0.25 基于湍流速度分布导出。
水头损失的两种形式
2 p1 v12 p2 v2 z1 1 z2 2 hw g 2g g 2g
hf hj
沿程损失
局部损失
流体克服粘性阻力 而损失的能量，流 程越长，损失越大
流体克服边界形状改变 所产生的阻力而损失的 能量，发生在局部范围
直圆管流动的沿程损失 1 达西公式 不可压缩粘性流体在内壁粗糙的直圆管中作定常流动时，压 强降低（损失）的表达式（可用量纲分析方法确定）
V12 V2 2 1 1 1 2 2 hm ( p1 p2 ) (V1 V2 ) V2 (V2 V1 ) 1 ( ) g 2g g 2g V1
V12 d12 2 V12 (1 2 ) K e1 2g 2g d2
d K e1 1 d
2. 等效粗糙度 穆迪引入等效粗糙度概念 。对实际商用管，粗糙度呈随机分 布，可通过与尼古拉兹实验曲线作对比，确定其等效粗糙度。 材料(新) 铆钉钢 ε(mm) 0.9～9.0
常用商用管的 等效粗糙度列于 右表中。
水泥 木板
铸铁 镀锌铁 镀锌钢 无缝钢
0.3～3.0 0.18～0.9
0.26 0.15 0.25 ～0.50 0.012 ～0.2
1 2
1
(
Re1＝4.22×104，查Mooddy图得λ2＝0.027 ,重新计算速度

第五章 管中流动解析

第五章 管中流动解析

Re≤2320 流型判据： 2320< Re<13800 或为湍流）
Re ≥ 13800
层流 过渡状态（或为层流
湍流
5.1.4 水力直径
过流断面面积A与过流断面上流体与固体 接触周长S之比的4倍来作为特征尺寸。这种尺 寸称为水力直径，用dH表示
dH
4
A S
式中 A ——过流断面面积；
S ——过流断面上流体与固体相润湿的 周界长，称为湿周。
湍流的剪应力: 由分子运动和质 点脉动所引起
e
du
dy
e 涡流粘度,它表征脉动的强弱.
Re为一无因次量，称为雷诺数。
雷诺数的物理意义：
Re
du
u 2 u d
惯性力 粘性力
Re越大，表示惯性越大，湍动程度越剧烈； Re小，表示粘性力占主导地位，湍动程度小。
这就是说，液体流动时的雷诺数若相同，则 它的流动状态也相同。另一方面液流由层流转变 为湍流时的雷诺数和由湍流转变为层流的雷诺数 是不同的，前者称为上临界雷诺数，后者为下临 界雷诺数，后者数值小，所以一般都用后者作为 判别液流状态的依据，简称临界雷诺数，当液流 实际流动时的雷诺数小于临界雷诺数时，液流为 层流，反之液流则为湍流，常见的液流管道的临 界雷诺数可由实验求得。
(2) 湍流 当流体微团间互相掺混作无序地流动，其流速、压力等力学 参数在时间和空间中发生不规则脉动的流体运动，称为湍流，又 称为紊流。湍流是在大雷诺数下发生的，其基本特征是流体微团 运动的随机性。湍流中由于这种随机运动而引起的动量、热量和 质量的传递，其传递率比层流高很多。它一方面强化传递和反应 的效果；另一方面剧增了摩擦阻力和能量损耗。
5.1 流动形态
5.1.1 雷诺实验

流体力学 第5章 圆管流动..

流体力学 第5章 圆管流动..

第5章圆管流动一.学习目的和任务1.本章学习目的（1）掌握流体流动的两种状态与雷诺数之间的关系；（2）切实掌握计算阻力损失的知识，为管路计算打基础。

2.本章学习任务了解雷诺实验过程及层流、紊流的流态特点，熟练掌握流态判别标准；掌握圆管层流基本规律，了解紊流的机理和脉动、时均化以及混合长度理论；了解尼古拉兹实验和莫迪图的使用，掌握阻力系数的确定方法；理解流动阻力的两种形式，掌握管路沿程损失和局部损失的计算；了解边界层概念、边界层分离和绕流阻力。

二.重点、难点重点：雷诺数及流态判别，圆管层流运动规律，沿程阻力系数的确定，沿程损失和局部损失计算。

难点：紊流流速分布和紊流阻力分析。

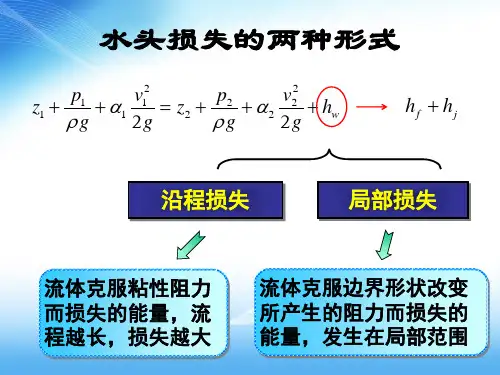
由于实际流体存在黏性，流体在圆管中流动会受到阻力的作用，从而引起流体能量的损失。

本章将主要讨论实际流体在圆管内流动的情况和能量损失的计算。

5.1 雷诺(Osborne Reynolds)实验和流态判据5.1.1 雷诺实验1883年，英国科学家雷诺通过实验发现，流体在流动时存在两种不同的状态，对应的流体微团运动呈现完全不同的规律。

这就是著名的雷诺实验，它是流体力学中最重要实验之一。

105如图5－1所示为雷诺实验的装置。

其中的阀门T1保持水箱A 内的水位不变，使流动处在恒定流状态；水管B 上相距为l 处分别装有一根测压管，用来测量两处的沿程损失f h ，管末端装有一个调节流量的阀门T3，容器C 用来计量流量；容器D 盛有颜色液体，T2控制其流量。

进行实验时，先微开阀门T3，使水管中保持小速度稳定水流，然后打开颜色液体阀门T2放出连续的细流，可以观察到水管内颜色液体成一条直的流线，如图5－2（a ）所示；从这一现象可以看出，在管中流速较小时，它与水流不相混和，管中的液体质点均保持直线运动，水流层与层间互不干扰，这种流动称为层流（Laminar flow ）。

比如，实际中黏性较大的液体在极缓慢流动时，属层流运动。

随后，逐渐开大阀门T3，增大管中液体流速，流速达到一定速度时，管内颜色液体开始抖动，具有波形轮廓，如图5－2（b ）所示。

流体力学实验_第五章

流体力学实验_第五章
28
§5.4 流动显示的光学方法
1. 适用范围 光学显示方法：利用流场的光学性质，如流体的密 度变化会造成光学折射率或传播速度的变化，通过 适当的光学装置可以显示流体的流动特性。
流场的温度、压力、浓度和马赫数等状态参数与密度 有确定的函数关系，而流体的光学折射率是其密度的 函数，因此下列流动可以采用光学流动显示的方法：
分光镜 补偿片
单色 点光 源
全反镜
风洞实验段
屏幕
40
密度均匀：干涉条纹彼此平行 密度不均匀：干涉条纹发生移动或变形，干涉条纹的改变与
流体密度的变化有关
干涉条纹 41
§5.5 流动显示技术的新发展——定量的流 动显示和测量技术
1. 激光诱导荧光（LIF）技术
激光诱导荧光技术：是一种20世纪80年代发展起来的光 致发光流动显示与测量技术，把某些物质（如碘、钠或 荧光染料等）溶解或混合于流体中，这些物质的分子在 特定波长的激光照射下能激发荧光。
照明光源：高亮度的白光碘钨灯
25
26
27
3. 荧光微丝法
采用直径为0.01 ~0.02mm的合成 纤维丝，经柔化 和抗静电处理， 使微丝染上荧光 物质，粘贴于模 型表面。
光源：采用连续 紫外光源
照相：选用合适 的滤光片
Flourescent minitufts on aircraft wing
在定常流动中，流线、迹线和染色线相同。
但在非定常流动中，是互不相同的。
4
3. 流动显示方法的分类
（1）示踪粒子流动显示：在透明无色的气流或水流中加
入一些可见的粒子，通过可见的外加粒子跟随流体微团的运 动来使各种流动现象显示出来。 固态示踪粒子：
水流（铝粉、有机玻璃粉末或聚苯乙烯小球等） 气流（烟颗粒） 液态示踪粒子：水流（牛奶、染料溶液） 气态示踪粒子：水流（氢气泡、空气泡）

第5章-圆管流动


e/d
Re
莫迪图λ
结论
0.03 0.1473 0.00102 1.732×106 0.02 用0.02重算
0.02 0.1358 0.0011 1.87×106 0.02
一致
d 0.298 1/5 0.1358m 即设计的最小管径为0.1358m
5.6 圆管湍流的沿程损失
5.6.3 非圆管的湍流沿程损失
——摩擦阻力系数，与
管径d、管中流速u和管 壁的光滑程度有关；
5.4 圆管中流体的湍流运动：
湍流剪应力分布与普朗特混合长度理论

1
2'


du dy


ux'
u
' y
平均值：
脉动值：
Re数较小时，1 占主导地位
Re数很大时， 2 1
牛顿内摩擦力 雷诺应力
y
u(y l')
第五章 圆管流动
内容提纲
5.1 雷诺实验与流态判据 5.2 圆管中流体的层流运动 5.3 椭圆管中流体的层流运动（自学） 5.4 圆管中流体的湍流运动 5.5 流体运动的两种阻力 5.6 圆管湍流的沿程损失 5.7 管路的局部损失 5.8 管路计算（自学）
按流体与固体接触情况来分，流体运动主要有下列四种形式。

1 2 umax
（层流时平均速度为最大速度的1/2）
5.4 圆管中流体的湍流运动：
湍流运动：三维随机运动，脉动性
瞬时速度 = 时均速度 + 脉动速度
u u u'
u 1
T
udt
T0
u' u u, 1 T u'dt 0

流体力学课件 第五章 流动阻力


斜直线分布
r hf 1 g grJ 2 l 2
du grh f dr 2l
抛物线分布
2.流速分布 3.流量
Q
r0 0
gh f 2 2 u (r0 r ) 4l
gh f 2 2 gh f 4 (r0 r ) 2 rdr d 4l 128l
（3）粗糙区
莫迪
§5-7 局部损失计算
一、边界层理论
1.边界层：贴近平板存在 较大切应力、粘性影响不能 忽略的这一层液体 。
2.边界层的厚度：当流速达到 边界层的厚度顺流增大，即δ是x的函数。
处时，它
3.转捩点，临界雷诺数 转捩点：在x=xcr处边界层由层流转变为紊流的过渡点。
临界雷诺数： Recr
三、总水头损失
hw h f h j
i 1 i 1 n n
§5-2 流体流动的两种型态
一、雷诺实验
1883年英国物理学家雷诺按图示试验装置对粘性流体进行 实验，提出了流体运动存在两种型态：层流和紊流。
1 4
(a)
hf 5
(b)
2
3
(c)
1.层流 ：管中水流呈层状流动，各层的流体质点互不掺混的 流动状态。
四、湍流切应力分布和流速分布
1.切应力分布
du 2 du 2 1 2 L ( ) dy dy
摩擦切应力 普朗特混合长度 ： 附加切应力
y L ky 1 r0
k 称为卡门常数
k 0.36 ~ 0.435
2.流速分布 （1）近壁层流层： 管壁切应力
du u 0 dy y
§5-6 湍流的沿程损失
一、湍流沿程损失计算

第五章 管中流动


一、时均流动与脉动
根据图所示的一点上的速度变化曲线，用一 定时间间隔T内的统计平均值，称为时均流 速 v 来代替瞬时速度，即
1 v T

T
0
vt dt
瞬时速度v与时均速度 v 之间的差值称为脉动 速度，用v’表示，即
v v v
想一想：湍流的瞬时流速、 时均流速、脉动流速、断面 平均流速有何联系和区别？
流体粘性切应力与附加切应力的产生有着本质的区别，前者是流体分子无 规则运动碰撞造成的，而后者是流体质点脉动的结果。
2. 混合长度理论
湍流附加切应力 t v vy 中，脉动流速 v , vy 均为随机量，不能直接计 x x 算，无法求解切应力。所以1925年德国力学家普兰特比拟气体分子自由程的概念， 提出了混合长理论。
p P h f gqV gqV pqV Fv g
2 128lqV P pqV d 4
七、层流起始段
流体以均匀的速度流入管道后，由于粘性，近壁处产生边界层，边界 层沿着流动方向逐渐向管轴扩展，因此沿流动方向的各断面上速度分布不 断改变，流经一段距离L后，过流断面上的速度分布曲线才能达到层流或 湍流的典型速度分布曲线，这段距离L称为进口起始段。
二、混合长度理论
1. 湍流流动中的附加切应力
t v vy 0 x
——雷诺切应力 雷诺切应力的时均值
t v vy x
在湍流运动中除了平均运动的粘性切应力 而外，还多了一项由于脉动所引起的附加 切应力，总的切应力为
dv v v x y dy
速度分布按对数规律，特 点是速度梯度小。
一、临界速度与临界雷诺数
上临界流速vc：层流→湍流时的流速。 下临界流速vc：湍流→层流时的流速。 vc < vc Re＝ vd/ 上临界雷诺数Rec ：层流→湍流时的临界雷诺数，它易受外界干扰， 数值不稳定。 下临界雷诺数Rec ：湍流→层流时的临界雷诺数，是流态的判别标准。 判别依据：

工程流体力学流体在圆管中的流动


l
流速分布
l
dr
d
p2
u
z2 z1
p1 dG
1
速度分布：u
gh f 4l
(r0 2
r2)
p
4l
(r0 2
r2)
其中 r0是圆管半径。
此处p，并不仅仅是 ( p1 p2 )，当且仅当，z1 z2时，p p1 p2。
可见:
速度和半径之间呈二次抛物线关系，管轴处流速达到最大。
2、流量
层流化；
• 利用控制湍流拟序结构来控制湍流取得了显著的成就，例如，
湍流减阻和降低噪声。
➢ • 湍流实验是认识湍流的重要工具，湍流研究也促进了流 体力学实验技术的发展；
➢ • 流场显示技术（氢气泡技术，激光诱导荧光技术等）和 湍流场的精细定量测量技术（粒子图像测速法等）相结合， 可以获得既直观又可靠的湍流场信息
流速增大时，颜色水看是动荡，但仍保持 完整形状，管内液体仍为层流状态，当到 达到某一值 v时k ，颜色线开始抖动、分散。 这是一种由层流到湍流的过渡状态。
当流速达到一定值时，质点运动曾现一种 紊乱状态，质点流动杂乱无章，说明管中 质点流动不仅仅在轴向，在径向也有不规 则的脉动现象，各质点大量交换混杂，这 种流动状态称为湍流或紊流。
2、动量修正系数
v2dA
A
V 2A
4 3
动能修正系数和动量修正系数都是大于1的正数，且 速度分布越均匀，则修正系数越小。
4.2.4 层流的沿程损失 沿程能量损失可以用压强损失、水头损失或功率损失 三种形式表示：
1、压强损失
由：V qV p R2 pd 4
A 8l 32l
移相，得：p 32l V KV
流体的流动状态与管径有关。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
粘性底层一般1 mm左右。
粘性底层 过渡区 湍流核心区
图3.4.2 湍流的速度结构
2012年12月15日 11
粘性底层虽然很小，但其作用不可忽视。 由于管子的材料，加工方法，使用条件，使用年限的影响，使得管壁 出现各种不同程度的凸凹不平，它们的平均尺寸△称为绝对粗糙度。 δ>△ 粗糙度对湍流核心几乎无影响， 水力光滑管 δ<△ 湍流核心流体冲击粗糙突起部位，引起涡旋，加剧湍乱程度， 增加能量损失， 水力粗糙管
来速度，到达新位置后，立刻和b层流体混合在一起，其速度变为b层速度。具 有了b层的时均速度。
2012年12月15日 5
vy 'dAv
该微团在x方向的原动量vy 'dAv
小于b层具有的动量
vy
'
dA(v
l
dv dy
)
和b层混合后，必然使b层流体动量在x方向上降低，引起瞬时 的速度脉动-vx。
对于原来流体微团来说，到达b层后，原来y方向的脉动转换 为x方向的脉动。如此反复，湍流脉动频繁的主要原因。
层流破坏后，在湍流中会形成许多涡旋，这是造成速 度脉动的原因，但理论上找脉动规律很困难。
统计时均法： 不着眼于瞬时状态，而是以某一个适当时间段 内的时间平均参数作为基础去研究这段时间内 湍流的时均特性。时间长短2、3秒一般足够。
2012年12月15日 2
1、时均流动与脉动
下图为一点上的速度变化曲线，用T时间段内的时间平均 值代替瞬时值，这一平均值就称作一点上的时均速度。
R
2012年12月15日 16
思考题
2.湍流研究中为什么要引入时均概念？湍流时，恒定 流与非恒定流如何定义？
3.湍流时的切应力有哪两种形式？它们各与哪些因素 有关？各主要作用在哪些部位？
把湍流运动要素时均化后，湍流运动就简化为没有脉动 的时均流动，可对时均流动和脉动分别加以研究。湍流 中只要时均化的要素不随时间变化而变化的流动，就称 为恒定流
粘性切应力——主要与流体粘度和液层间的速度梯度有 关。主要作用在近壁处。 雷诺切应力——主要与流体的脉动程度和流体的密度有 关，主要作用在湍流核心处脉动程度较大地方。
2012年12月15日 17
4. 湍流中为什么存在粘性底层？其厚度与哪些因素有关？其厚度 对湍流分析有何意义？
在近壁处，因液体质点受到壁面的限制，不能产生横向运 动，没有混掺现象，流速梯度du/dy很大，粘滞切应力 τ=μdu/dy仍然起主要作用。
二 混合长度理论
Prandtle 创立，为解决湍流中切应力、速度分布及阻力计算问 题奠定了基础。
取如图坐标，假设a,b两层流体，
a层时均速度 v v( y)
b层时均速度
vl dv dy
设想在某一瞬时，在a层有一个流体微团，经过微元面积dA以vy’的脉动 速度沿y轴正向跳动，其质量流量为 vy ' dA ,到达新位置前，其速度为原
dy
式中L称为混合长度。
2012年12月15日 8
这样，湍流的时均切应力由两部分组成，
粘性切应力+脉动切应力 dv L2(dv)2
dy
dy
有时也可统一形式 ( ) dv
dy L2 ( d v ) 称为湍动粘度或虚粘度，
dy 并非流体本身的物理属性
说明： 1）在雷诺数较小时，脉动较弱，粘性切应力占主要地位。 2）雷诺数较大时，脉动程度加剧，脉动切应力加大，在已充分发展的
(S
S
')dt
S
1 T
T 0
S
'
dt
脉动量的时均值为零
1
t
t 0
S
'
dt
0
运用统计时均法将湍流流动分成时均流动，脉动运动两部分。 时均流动：代表主流，重点是这些主流特征:包括速度分布， 切应力分布，流量及阻力计算公式等； 脉动运动：反应湍流本质，使湍流与层流有巨大差距所在。
2012年12月15日 4
1
dv dy
2
L2 ( dv )2 dy
r<0.7R时，粘性切应力几乎不起作用，以脉动为主的湍流核心。
r=0.95R时，脉动应力最大。
r>0.95R时，脉动切应力迅速降为0，以粘性切应力为主的粘性底层。
在过渡层中，两种切应力都存在。
2012年12月15日 14
3 速度分布
在粘性底层中
1
dvx dy
2012年12月15日 10
三 管中湍流的切应力分布
管中为层流时，全管中都是层流状 态，分布规律适合于整个过流断面。 湍流时：
1 粘性底层、水力光滑管与水力粗糙管
靠近管壁以层流为主，称为粘性底层。粘 性底层的厚度不是固定不变的，他与 , v, 有关，粘性底层的厚度可用公式计算近似 计算
32.8d Re
2012年12月15日 18
作业: 1、写出湍流中物理量的时均值的表达式并进行解释. 2、写出混合长度理论表示的湍流切应力的表达式? 3、什么叫水力光滑管和水力粗糙管? 练习: 8, 9
2012年12月15日 19
5.4 管路中的沿程阻力
沿程阻力是造成沿程水头损失的原因。用达西公式计算，探
讨公式中
解:
V
4Q
d 2
1.019m / s
水的运动粘度
1.007106 m2 / s Re Vd 2.53105
/d=1.210-3 ,查莫迪图, =0.021, 故
h
l d
V2 2g
0.445m(水柱)
2012年12月15日 25
解题步骤: 1 计算雷诺数 2 查找表面粗糙度,计算 3判断阻力区域类型, 选择相应的公式计算阻力系数 4 根据公式计算沿程水头损失
2012年12月15日 13
2 切应力分布规律
0
(
p1
p2 )R 2l
p l
R 2
p r l2
0
r R
过流断面上切 应力K字形分 布规律。层流 和湍流见图。
湍流中切应力包括粘性切应力与脉动
层流与湍流的切应力分布
切应力，但这两种切应力在粘性底层
和湍流核心中所占的比例是不同的
在粘性底层，脉动切应力很小，主要是粘性应力 在湍流核心处，由于速度分布均匀，速度梯度很小， 脉动剧烈，因而主要是脉动切应力。 轴心处，速度梯度为0，切应力为0。
湍流中，粘性切应力与脉动切应力相比忽略不计。 3）沿断面切应力分布不同，近壁处以粘性切应力为主（称粘性底层）
2012年12月15日 9
思考题1： 湍流的瞬时流速、时均流速、脉动流速、有何 联系和区别？
瞬时流速 ，为某一空间点的实际流速，在湍流流态 下随时间脉动； 时均流速，为某一空间点的瞬时速度在时段T内的时 间平均值； 脉动速度与时均速度的叠加等于瞬时速度；
二 莫迪图 对于工业用管，为应用方便，绘出了莫迪图，图中绝对粗糙度是 测量出的。表中也有一些常用值。
求取有三种方法：图线法，图表法和计算法。
2012年12月15日 23
例 消防水龙带直径为100mm,长为20m,要求流量为0.1 l/s, 求沿程水头损失。
Re
vd
d2
0.0001 *1.007 *106
粘性底层厚度与雷诺数、质点混掺能力有关 随Re的增大，厚度减小。 粘性底层很薄，但对能量损失有极大的影响。
5.湍流时断面上流层的分区和流态分区有何区别？
粘性底层，湍流核心：粘性、流速分布与梯度; 层流、湍流：雷诺数
6.圆管湍流的流速如何分布？
粘性底层：线性分布; 湍流核心处：对数规律分布或指数规律分布。
0.2 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg(Re)
2012年12月15日 21
理论和半经验公式较准确但复杂，经验公式准确性较差但计 算方便，有时可作理论公式的迭代初始值，迭代2,3次即可。
2012年12月15日 22
f (Re, )
d
一 尼古拉兹实验
1933年的实验，砂粒涂于管 道内壁，六种粗糙度，对不 同Re做实验：
hf l v2
2pd
lv 2
d 2g
2012年12月15日 20
lg(100)
1.1 1.0
0.9
0.8
I
0.7
0.6
0.5
II
0.4
0.3
d/
V
30
61
IV
120
252
504
III
1014
vx
0 1 ln y C k
2012年12月15日 15
k=0.4，C由边界条件确定。 假设光滑管湍流核心的边界 是它粘性底层的交界面。
vx
0
y
vx
0 1 ln y C k
y
,vx
0
,C
0
0 1 ln k
vx
0 1 ln y 0 k
式中粘性底层厚度 管壁面上的切应力
, dvx
1
dy
粘性底层很薄，可以近似 用壁面上切应力表示，于 是积分可得
vx
0
y
为直线
在湍流核心区：
2
L2 ( dv )2
dy
湍流核心中速度和y呈对数关系
0
r R
0 (1
y) R
L ky 1 y R
卡门实验得到
0 (1
y) R
k
2
y2 (1
y )( dvx R dy
)2
dvx
0 dy ky
32.8d 32.8 Re v
0
pd 4l
p