当前位置：文档之家 › 第四章 湍流流动

第四章 湍流流动

  • 格式：ppt
  • 大小：417.00 KB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

6.湍流流动

6.湍流流动


µ eff = µ 1 + µ τ
∂p − ∂x
∂ v′ 2 ∂ v′ v′ ∂ v′ v′ ∂ 2vx ∂ 2vx ∂ 2vx ∂v x ∂vx ∂vx = µ 2 + 2 + 2 − ρ x + y x + z x ρ vx + vy + vz ∂x ∂x ∂x ∂y ∂z ∂y ∂z ∂y ∂z
时均化与偏微分相互独立，表现在数学上，可交换运算次序。 凡有带脉动瞬时量的乘积项存在时，就多出一项：单个带脉动的瞬时量 时均化时，相当于把瞬时量换成时均量；对于带脉动瞬时量的乘积项， 除把瞬时量换成时均量外，还多出一项－－脉动量乘积的时均量。 冶 金 传 输 原 理 制 方 程 控
∂vz ∂v z = ∂x ∂x
∂ v′2 ∂ v′y v′ ∂ v′ v′ ∂ 2vx ∂ 2vx ∂ 2vx ∂v x ∂v x ∂v x x = µ 2 + 2 + 2 − ρ x + ρ vx + vy + vz + z x ∂x ∂x ∂x ∂y ∂z ∂y ∂z ∂y ∂z
6.3 湍流流动的定解问题
混合长度模型
τ ij = − ρ vi′v′j = ρL2 m
冶 金 传 输 原 理
应用时间最长，经验最丰富的一种湍流粘 性系数模型，优点在于模型简单。 局限：它认为湍流脉动速度与当地时均速 度梯度成正比，因而速度梯度为0时，脉动 速度也为0，与客观事实不符； 因为代数方程模型不能反映湍流过 程中特征量的对流与扩散作用，不能应用 于复杂的边界类型流动。 普朗特假设：
单方程模型
∂ vi ∂ vi ∂x j ∂x j
流体力学第4章流体流动基本原理

流体力学第4章流体流动基本原理

定义 流体质点集合 流场空间
特性 与外界 关系 主要 特征
对应方法
形状、位臵变化 力的作用 能量交换 无质量交换 质量 不变
拉格朗日方法
位臵、体积、形状确定 力的作用 能量交换 质量交换 质量随时间 变化
欧拉方法
9
由于有关物质运动的基本原理都是针对具有确 定质量的系统而言的，所以，以控制体为研究对象 时就存在这样一个问题：
mCV qm2 qm1 0 t
28
对稳态流动系统，流体及流动参数均与 时间无关，即
mCV / t 0
因此，质量守恒方程简化为
qm1 qm2
或 1v1 A1 2v2 A2
即稳态流动，输入与输出的质量必然相等。
29
对不可压缩流体的稳态流动，ρ=const，则
v1 A v2 A2 1
15
引入t+Δt时刻区域I的质量。于是上式得
(dm / dt)系统 mII |t t mIII |t t mI |t mII |t mI |t t mI |t t lim t 0 t (mII mI ) |t t (mII mI ) |t lim t 时刻的 t+Δt 时刻的 t 0 t 系统边界 系统边界 III mIII |t t mI |t t I II ( lim lim ) t 0 t 0 t t 固定的 t 时刻的流
质量不变是系统的特点。
1
2
3
5
以系统为对象研究流体运动，就必须随时对系 统进行跟踪识别其边界，这在实际流动过程中显然 是很困难的。
工程上所关心的问题也不在于跟踪质量确定的
流体的运动，而在于确定的设备空间中流体的流动
行为。
《湍流流动模型》课件

《湍流流动模型》课件


• 混合模型：结合基于方程的模型 和基于统计的模型的特点，通过 混合这两种方法来描述湍流流动 。如SST k-ω模型和修正后的k-ε 模型等。计算量适中，精度较高 ，适用于多种工程应用场景。
03 湍流流动模型的建立与求解
湍流流动模型的建立
湍流现象的描述
湍流是流体的一种复杂流动状态，具有高度的不规则性和 随机性。为了理解和模拟湍流，需要建立一个数学模型来 描述其基本特征和规律。
3
纳维-斯托克斯方程的满足度
检验模型是否满足纳维-斯托克斯方程，以评估 模型的物理意义和准确性。
湍流流动模型的应用Байду номын сангаас例
航空航天领域
湍流流动模型用于研究飞行器在高速飞行时 产生的湍流流动现象，以提高飞行器的性能 和安全性。
能源与环境领域
湍流流动模型用于模拟燃烧过程、流体机械内部流 动等复杂湍流现象，以提高能源利用效率和环境保 护水平。
化工与制药领域
湍流流动模型用于研究化学反应过程中产生 的湍流流动现象，以提高化学反应效率和制 药工艺水平。
05
湍流流动模型的发展趋势与展 望
湍流流动模型的发展趋势
多尺度模拟
随着计算能力的提升，湍流流动模型正朝着多尺度模拟的方向发 展，以更准确地模拟湍流在不同尺度上的行为。
非线性模型
传统的线性模型在处理复杂湍流时显得力不从心，非线性模型的研 发和应用成为新的趋势。
基于本征方程的模型
本征方程模型
通过求解湍流的本征方程来描述湍流 流动。本征方程基于湍流的物理特性 ，能够更准确地描述湍流流动。但计 算量大，对计算机性能要求高。
简化的本征方程模型
为了减小计算量，对基本的本征方程 进行简化处理，如忽略某些项或采用 近似解。计算量相对较小，精度有所 降低。
CFD第四章解读

CFD第四章解读

其他变量的时均输运方程
u j u j S t x j x j x j
uiu j
2019/2/24
ij
Reynolds应力 （6个）
3
4.2
直 接 数 值 模 拟 DNS 非 直 接 数 值 模 拟 大 涡 模 拟 LES
2019/2/24
6
4.2
湍流的数值模拟方法简介
4.2.3 Reynolds平均法（RANS）
不直接求解瞬时的N-S方程，而是想办法求解时均化的 Reynolds方程。这样，不仅可以避免DNS方法的计算量大的 问题，而且对工程实际应用可以取得很好的效果。Reynolds 平均法是目前使用最为广泛的湍流数值模拟方法。 Reynolds方程中有关于湍流脉动值的Reynolds应力项 ， 这属于新的未知量。因此，要使方程组封闭，必须对 uiu j 作出某种假定，即建立应力的表达式（或引入新的湍流模型方 程），通过这些表达式或湍流模型，把湍流的脉动值与时均值 等联系起来。
k kui k k t Gk t xi x j x j
u i C1 2 G k C 2 t t xi x j x j k k
u i u j k x t x x i j j
3/ 2 u i k C D x l j
• 由Kolmogorov-Prandtl表达式，有 t C kl • 其中， k , CD , C 为经验常数。 l 为湍流脉动的长度 比尺，依据经验公式或实验而定。 • 一方程模型考虑到湍动的对流输运和扩散输运， 因而比零方程模型更为合理。但是，一方程模型中如 何确定长度比尺 l 仍为不易解决的问题，因此很难得 到推广应用。
第四章 层流、湍流与湍流流动

第四章 层流、湍流与湍流流动


gz

1

p
z
1 r r
r
vz r


2vz z 2

边值条件：
v z r
r 0
0,vz
r R
0
vr r
r 0
0,vr
r R
0
⑵问题简化：设L为足够长→无限长，流动达到稳态后速度分
布与z无关
vz 0 z
2v z z 2
0
vr 0
r方向：
1 p 0
r
z方向：
gz

1

p z

1 r
r
r
vz r


0
1

dp dz
gz

1 r
r
r
vz r

dp dz

gz


1 r
r
r
vz r

1

p p1




v 说明：p 减小， 变大，直到 p p0 止。
2．一维稳态等熵流动的基本特性
由连续性方程：G A1v11 Axvx x
Ax
G
vx x
A 为截面面积。
1
将速度式及代入上式：x


1

px p1


Ax
G
4.2 层流流动的定解问题
求解实际流体的流动问题应用连续方程和运动方程。对于不可压缩及 粘性为常量的情况下方程组封闭。否则，需补充状态方程、温度场方 程等。我们首先分析定解条件。 1． 初值问题：
第四章 湍流流动

第四章 湍流流动


ux，P为瞬时速度及压力，是时间的函数。
3
瞬时参数值等于时均值与脉动值之和。
___
如： ux ux ux'
___
uy
u
y
u
' y
___
uz uz uz'
___
p p p
ux' ,u'y ,uz' ——脉动速度分量;
p ——脉动压强.
根据以上定义，在时间θ内脉动值的平均值应为零，即：
___
②
xx
x
x
___
xx
__
稳定流动，时均速度 u x 不随时间变化
____
___
____
③ ux2 ux2 ux' 2
x x x
______
___
yx yx
y y
11
______
___
④同理： zx zx
z z
_______
uzux
__
uz
__
ux
______
uz' ux'
ux y
u
' y
C1ux'
C1C2l '
ux y
∴
___
r yx
C1C2l
'
__
ux
y
C2l
'
__
ux
y
C1C22l '2
__
ux
y
2
l2
__
ux
2
y
26
式中： l 2 C1C22l '2
或 l C1C22 l'
第四章 层流流动与湍流流动

第四章 层流流动与湍流流动

第四章层流流动及湍流流动由于实际流体有粘性，在流动时呈现两种不同的流动形态：层流流动及湍流流动，并在流动过程中产生阻力。

对可压缩流体，阻力使流体受压缩。

对不可压缩流体，阻力使流体的一部分机械能转化为热能散失，这个转变过程不可逆。

散失的热量称为能量损失。

单位质量（或单位体积）流体的能量损失，称为水头损失（或压力损失），并以h w（或Δp）表示。

本章首先讨论流体的流动状态，再对粘性流体在两种流动状态下的能量损失进行分析。

第一节流动状态及阻力分类一、流体的流动状态1．雷诺试验：1882年雷诺作了如教材45页图4-1所示的流体流动形态试验。

试验装置：在圆管的中心用细玻璃管向圆管的水流中引入红色液体的细流。

试验情况：（1）当水的流速较小时（图4-1a），红色液体细流不与周围水混和，自己保持直线形状与水一起向前流动。

（2）如把水的流速逐渐增大，至一定程度时，红色细流便开始上下振荡，呈波浪形弯曲（如图4-1b）。

（3）当再把水流速度增大，红色细流的振荡加剧，至水的流速增大至某一速度后，圆管中红色细流消失，红色液体混入整个圆管的水中（如图4-1c）。

试验的三种不同状况说明：（1）对（图4-1a）所示，表明水的质点只有向前流动的位移，没有垂直水流方向的移动，即各层水的质点不相互混和，都是平行地移动的，这种流动称为层流；（2）对（图4-1b）所示，说明流动的水质点已开始有垂直水流方向的位移，离开圆管轴线较远的部位水的质点仍保持平行流动的状态；（3）对（图4-1c）所示，说明流动中水的质点运动已变得杂乱无章，各层水相互干扰，这种流动形态称为紊流或湍流。

2．雷诺数：流体之所以出现不同的流动形态，主要由流体质点流动时其本身所具有的惯性力和所受的粘性力的数值比例决定。

惯性力相对较大时，流体趋向于作紊流式的流动；粘性力则起限制流体质点作纵向脉动的作用，遏止紊流的出现。

雷诺根据此原理提出了一个判定流体流动状态的无量纲参数——雷诺数（Re）：对在圆管中流动的流体而言，雷诺数的表现形式为v：圆管内流体的平均流速（m/s）；ε：动力粘度（Pa·s）。

第 四章湍流2012

第 四章湍流2012

' 2 ' i
35
1.介绍
1.6 雷诺应力
比较N-S方程和雷诺方程，雷诺方程里面
' ' 出现了一项： ui u j , x j
这项来源于脉动运动对平均运动的影响。

雷诺应力：
ij u u
' i
' j
36
1. 介绍
1.6 雷诺应力
总应力： T p 2 e u ' u ' ij ij ij i j
42
q
2
'2 u1
2. 湍流半经验理论
1.2 普朗特混合长度理论
• 气体分子运动论 • 动量传递 • 分子运动和碰撞
0.499c 平均自由程
• 湍流
无规则运动

动量输运
43
2. 湍流半经验理论
1.2 普朗特混合长度理论
考虑平行剪切流 q ( y) y
v'
y l
q ( y l)
3.5 CH JL k- SST YS CMOTT SHIH TS Exp. 3.0
2.5
P/P1
2.0
1.5
surface pressure of 2-D Compcompression corner M=2.84
1.0 -0.2 -0.1 0.0 0.1 0.2
s(m)
4
1.介绍
2-D压缩拐角摩擦力分布M=2.84
U U 1 j i eij 2 x x i j
湍流压力：
1 ' ' pt ui ui 3
37
2. 湍流半经验理论
第四章 层流、湍流与湍流流动详解

第四章 层流、湍流与湍流流动详解

边值条件：
2 v z v z r 2 r z
v z r
vr r
0,v z
r 0
r R
0
0,vr
r 0
r R
0
⑵问题简化：设L为足够长→无限长，流动达到稳态后速度分 布与z无关
v z 0 z
2v z 0 2 z
1 p 0 r
变动量方程为：
2v x 1 p X方向：0 x y 2
g Y方向：
1 p y
2 ⑶简化后的方程为：C 1 p d v x 1 x dy 2 C 则得： v x 1 y 2 Dy B 2
由边界条件：（y=0时，y=h时）
B 0 ， D v 0 1 p h
2v y 2v y 1 p Y方向： v x x v y y g y x 2 y 2 v y v y
边值条件：
v x v x
y 0 y h
0, v0 ,
vy
y 0
0 0
vy
y h
度与固体壁面保持相对静止：
v t t ,x ,y ,z w v w t ,x ,y ,z
v w ：固体壁面的切线速度。
在与固体边壁垂直方向上，流体不能穿透而进入固体之内，即：
vn t ,x ,y ,z w 0
② 对称边值条件。
对称面：物理量在对称面上的变化率为零。 如：管道流中坐标选在管道中心线上时：
4.2 层流流动的定解问题
求解实际流体的流动问题应用连续方程和运动方程。对于不可压缩及 粘性为常量的情况下方程组封闭。否则，需补充状态方程、温度场方 程等。我们首先分析定解条件。 1． 初值问题： 非稳态问题需给出初始时刻值： 0 x ,y ,z 2． 边值问题（边界值）： ① 固体壁面无渗透、无滑移边界条件贴近固体壁面处一层流体的速
湍流流动模型-带作业

湍流流动模型-带作业


•
在工程上, 我们最感兴趣的是各种流体力学量的平
均值, 以及它们在平均值周围的变化范围, 有时也须
知道各种量之间的关联大小。然而这些量的平均值
如何确定, 这在湍流中是一个有争议的间题。
4-1-3平均量输运方程
• 现在着手建立平均量输运方程, 为容易理解起见,
首先讨论不可压缩流体。把各种参数都分解为平
4-4 双方程模型
• 为了考虑对流和扩散对湍流尺度的影响, 除了湍流动能方
程以外, 还须建立湍流尺度的微分方程。在双方程模型中,
假定式(4-27)和式(4-37)成立。初期人们尝试了各种各样
的湍流尺度的微分方程, 但在使用中都不很成功。
• 后来发现, 用各向同性耗散率作为变量, 建立微分
方程, 并用耗散率模拟式
还增加了密度脉动、速度脉动的二阶关联量和三阶关联量, 这
些量反映了密度的变化在湍流中起相当大的作用, 方程变的很
复杂。
作业: 推导上述平均方程。
• 与式(4-18)比较可看出, 在用法夫雷平均得到的输运方程
中, 没有出现与密度脉动有关的项, 使方程得到了很大的
简化, 且平均参数的物理意义有时也比简单时间平均值清
成不封闭了。
• 从瞬时参数的守恒方程出发, 可以推出各种二阶
关联量的输运方程。但很快就发现, 在这些二阶
关联量的输运方程中, 又出现了三阶关联量, 同样,
在三阶关联量的方程中, 出现四阶关联量, 如此等
等。
• 很明显, 从基本的方程出发, 无法解决不封闭问题。
• 目前, 我们一般都采用模型封闭的办法, 即用量纲
• 测量表明, 当流动雷诺数较大时, 湍流的涡旋尺寸分布可
以明显地区分为含能涡旋区、惯性区和耗散区。
传输原理-层流与紊流

传输原理-层流与紊流

传输过程原理（课程编号：30120172）2003.9.27沈厚发焊接馆308电话：89922Email：shen@第四章层流流动及湍流流动第一节流动的状态及阻力分类第二节流体在圆管中的层流流动第三节流体在平行平板间的层流流动第四节流体在圆管中的湍流运动第五节沿程阻力系数的确定第六节局部阻力本课学习内容雷诺实验Reynolds (1882)层流过渡状态湍流第一节流动的状态及阻力分类层流（流线型流）：流线呈平行状态的流动。

流体质点在流动方向上分层流动，各层互不干扰和渗混特点：流速很小、粘度很大平壁面绕流的边界层边界层（附面层Boundary Layer ）：由速度为零的壁面到速度分布“较均匀”的区域。

流体的粘性在贴近物面极薄的一层内主宰流体运动。

管内层流速度的发展1.1 层流与边界层层流起始段长度（AC ）：l = 0.065dReA B湍流质点的运动湍流：流体流动时，各质点在不同方向上作复杂的无规则运动，互相干扰地向前运动。

湍流运动在宏观上既非旋涡运动，在微观上又非分子运动。

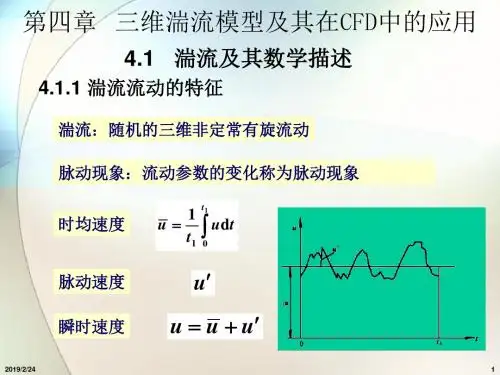
流体质点的运行路径v xtv x 湍流脉动：在总的向前运动过程中，流体微团具有各个方向的脉动。

在湍流流场空间中的任一点上，流体质点的运动速度在方向和大小上均随时间而变。

瞬时平均速度：瞬时速度在一定时间内 t 内的平均值。

管内湍流中心区域特征：流体“层”与“层”之间粘性摩擦阻力小（可忽略），相对速度很小；湍流中的流动阻力（及动量交换）主要由流体微团的无规则迁移、脉动引起。

湍流主流湍流边界层层流底层湍流起始段长度：l = 25~40 d惯性力愈大，层流趋向于紊流转变；惯性力愈小，紊流趋向于层流转变。

粘性力惯性力===νηρDv D v Re 式中：v －流体在圆管中的平均速度（m/s ）；D －圆管内径（m ）。

雷诺数（Reynolds Number ）：惯性力和粘性力比。

对于在管内强制的流体，由层流开始向湍流转变：Re cr ≤2320层流（Recr 临界雷诺数）；Re cr ’≥13000湍流（Re cr ’上临界雷诺数）；2320＜Re ＜13000，流动处于过渡区（不稳定），可能是层流、也可能是湍流。

第4章 简单剪切湍流.ppt

4.1.2 壁湍流的湍涡结构和湍涡粘性系数
圆锥形涡生成的脉动速度场有以下形式
四、简单剪切湍流
式中，x0 , z0 是锥形湍涡顶点的坐标；u0 (x x0 ) 是沿圆锥轴 向变化的脉动速度。 de de(x x0 ) 是圆锥沿轴向变化的直径。
由于近壁层中 de 是小量， u0 (x x0 ) 是缓变函数，所以
右图为利用VITA条件采样的二维脉动速度分布考察雷诺应力。
4.6 拟序结构的动力学模型
4.6.1 拟序运动的分解和能量输运
1、拟序运动的分解和能量输运
四、简单剪切湍流
拟序相：触发拟序结构的时空坐标 拟序事件：由拟序相触发的一次拟序运动 拟序平均：拟序事件的相平均 拟序分解：将湍流样本流场分解为拟序相平均与拟序脉动 拟序扰动：拟序相平均和全系综平均的差
4.1 简单剪切湍流的统计特性
4.1.1 壁湍流的统计特性和湍涡结构
直槽中流动的平均运动方程为
积分
四、简单剪切湍流
式中， 是分子粘性应力和雷诺应力之和，称为总切应力； 0是壁面切应力。
以上公式说明在槽道湍流中，总切应力是y的线性函数。
四、简单剪切湍流
4.1 简单剪切湍流的统计特性
4.1.1 壁湍流的统计特性和湍涡结构
四、简单剪切湍流
4.4 剪切湍流中的拟序运动
4.4.2 湍流边界层的拟序结构
1．湍流边界层拟序结构的实验观测
四、简单剪切湍流
4.4 剪切湍流中的拟序运动
4.4.2 湍流边界层的拟序结构
1．湍流边界层拟序结构的实验观测
在线性底层，有狭长 的低速带状氢气泡积 聚，形成有横向准周 期性的条带，称之为
条带结构。随着显
湍流 第四章
简单剪切湍流

[工学]湍流流动

流速分布曲线
τ
y
τ
二是流层的波动。在流动着的流体中，如果由于某种原因，流层 发生轻微的波动，则流层凸起的地方将因微小流束截面的减小而 使流速增大；反之，在凹入的地方，将因微小流束截面的增大而 使流速减小。根据柏努利方程，流速的增大将引起压力的减小， 而流速的减小将引起压力的增大。这样一来，轻微波动的流层就 将承受横向压力。
(5-42)
(3)湍流主体(y＋≥30)
u 2.5ln y 5.5
(5-43)
式(5-41)～式(5-43)即为光滑圆管湍流时的通用速度分布方程。这是一个 半经验半理论公式，它存在明显的局限和不足，例如用式（5-43）计算 得到的管中心速度梯度并不为零，而实际在管中心的速度梯度等于零。 尽管如此，上述通用速度分布方程仍然能够满足工程计算的要求。
此外，圆管中稳态湍流的速度分布亦可用如下形式的经验公 式近似地表示
y u umax ri
1/ n
r umax 1 ri
1/ n
4×104<Re<1.1×105时，n=6； 式中，指数 n 随Re数的变化而变化。 1×105<Re<3.2×106时，n=7； Re>3.2×106时，n=10 。 流体输送中较常遇到的Re值范围在~105左右，故1/7次方定律应用的较 为普遍。但它只是近似的，特别是不能表达壁面处的情况。因为在壁 面处其速度梯度→∞ ，这显然与实际不符。
u y l
d ux dy
将脉动速度表达式带入（5－12）中，有

引入比例系数c1
r yx
dux 2 l ( ) dy
2
r yx c1 l 2 (
dux 2 ) dy

湍流流动的特点与反应流基本方程


x j
(h
H~ x j
l
l H~l
ml x j
)
Sh
(30)
上述时均方程的通用形式：
t
(
'')
x j
( v j
vj'' vj ''
'vj'
' v j '')
x j ( x j ) S
式中 为1、 vi、ml及 H~时，即分别表示上述四个时均方程。
（31）
17
大多数湍流计算中，密度和其它量的关联程度很小 忽略密度脉 动关联项及所有三阶关联项，则上式简化为（下述方程的因变量都是 平均量，为清楚起见，略去符号上的短横）：
（1）连续性方程（质量守恒方程）
t
x j
(v j
)
0
在直角坐标系中，上式第二项可写成下列分量形式：
（17）
x1
(v1 )ຫໍສະໝຸດ x2(v2 )x3
(v3 )
（17a）
11
（2）动量平衡方程
t
(vi )
x j
(v jvi )
ij
x j
Svi
（18）
式中
ij
p ij
( vi
x j
v j x i
（1）湍流流场具有完全不规则的瞬息变化的运动特征。
（2）湍流流场中，各种物理量都是随时间和空间变化的随机量。
（3）湍流流场中，流体微团的随机运动在足够长的时间内服从某种数 学统计规律。空间点上任一瞬时物理量均可用平均值与脉动值之和来 表示，即
u u u p p p
v v v T T T c c c

第四章 管内流动与水力计算

沿x轴取一长为dx、 半径为 r 的同轴圆柱形 控制体。
在充分发展的定常层流流动条件下， 作用在控制体上的合外力为零。
外力主要有：控制体两端 的压力、侧面的粘性切应力 以及重力（忽略控制体 的流体重力），并认为两端的 压强分布均匀，可以写出控制体的力平衡式：
控制体的力平衡式为：
pr2 ( p p dx)r2 2rdx 0
2、管内湍流时均运动的速度分布
圆管内湍流时均速度分布可分层表达为：
粘性底层
y 0 y* 5
u
u*
y y*
过渡层
5 y 30 y*
u 5.0 ln y 3.05
u*
y*
湍流核心区
y y*
30
u u*

2.5 ln
y y*
5.5
y 坐标自管壁指向管道中心u*。 w — 壁面摩阻流速；
▪ 局部损失：发生在连接元件附近的损耗。 流体不仅沿流道向前运动，还有大量的碰 撞、涡旋、回流等发生。
公式表达
▪ 总损失
m
n
h w12 hf hj
▪ 沿程损失 ▪ 局部损失
hf

L V2 D 2g
hj

V2 2g
第二节 圆管内的层流与湍流
一、圆管内的层流流动
设有一无限长水平直圆管，其半径为 R， 对称轴为 x 轴，径向为 r 轴，流体沿 x 轴向作 充分发展的定常层流流动。

hf
/
L D
2
2g
1.13
由于是层流流动
64
Re
可得： Re 64 56.6

得该润滑油的运动粘度： D 1.82 104 m2/s

流体力学5粘性流体湍流流动

对于水力粗糙管：
1

2.0 lg
d 1.74 2
h f um
2
d （尼古拉兹粗糙管公式） 4lg 3.7 r 1 2.0 lg 0 1.74 若定义 d / 2 r0 ，则

1
2
平方阻力区
层流区
f (Re) 64
0 u*
水力光滑管的流速分布
u0 u* y 1 7 8.74( ) u*
水力粗糙管的流速分布
u0 y 8.5 2.5 ln( ) u*
其中 为层流底层的厚度
d 30 Re
4.3
圆管中的摩擦阻力系数
根据理论和实验分析 ，影响压降的因素有 d , , , v, L, 等， L 依π定理进行推导，得出 p f ( , ) 2 v vd d d
边界层定义：速度梯度很大的薄层。粘性在该薄层内起作用。
U0 y U0 0.99U0
U0
u(x,y) o
(x) x
L
平壁面绕流的边界层
Prandtl边界层模型——全流场分成二个流动区域。 边界层厚度(x)定义：流速从0增至0.99U0处的y值。 外区（y>）：速度梯度很小，可略去粘性的作用。 内区（y<）：速度梯度很大，考虑粘性。
L v 2 p p1 p2 d 2
在比较广泛的Re数范围内，取尼古拉兹光滑管公式：
10 Re 3 10 :
5 6
0.221 0.0032 0.237 Re
若流动为Re<105的湍流，采用卜拉休斯阻力公式：
4000 Re 105 :
平均流速 v 与Re、构成隐函数的关系，需用迭代方法求解。

湍流流动


时均值:取一时间间隔，使之 比湍流的振荡时间要长得多，比 vxi 宏观特征时间又要短得多，在该 时间间隔内做时间平均
时均速度 v x = 脉动速度 v′ x , 瞬时速度 v xi = vx + v x
v′ x
1 Δt v xi dt Δt ∫0
vxi
o
Δt
vx
t
时均参数不随时间改变的紊流流动 瞬时轴向速度与时均速度图 称为准定常流动或时均定常流
∂Vy ∂t
+
∂VxVy ∂x
+
∂VyVy ∂y
+
∂VzVy ∂z
∂ 2Vy ∂ 2Vy ∂ 2V y 1 ∂p =− +ν ( 2 + 2 + 2 ) ∂x ∂y ∂z ρ ∂y
∂Vz ∂VxVz ∂VyVz ∂VzVz ∂ 2V ∂ 2V ∂ 2V 1 ∂p + + + =− +ν ( 2z + 2z + 2z ) ρ ∂z ∂t ∂x ∂y ∂z ∂x ∂y ∂z
2
方程组（14）就是著名的不可压缩流体作湍流运动时的时均运 动方程称为雷诺方程。 将时均运动方程（ 14 ）和N—S方程（12a）相比可以看出，湍 流中的应力，除了由于粘性所产生的应力外，还有由于湍流脉 动运动所形成的附加应力，这些附加应力称为雷诺应力。雷诺 方程与N—S方程在形式上是相同的，只不过在粘性应力项中多 出了附加的湍流应力项。 以上导出 的雷诺方程和连续方程中，除过要求解的四个变 Vy 、 Vz 和 p 外，还有与脉动速度有关的如 V 'x V 'x 、 V 'x V ' y 等 量 Vx 、 六个未知数。四个方程中有十个未知数，即方程组不封闭。要 使方程组封闭，必须补充其它未知量的关系式才能够进行求 解。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

②
xx
x
x
___
xx
__
稳定流动，时均速度 u x 不随时间变化
____
___
____
③ ux2 ux2 ux' 2
x x x
______
___
yx yx
y y
11
______
___
④同理： zx zx
z z
_______
uzux
__
uz
__
ux
______
uz' ux'
___ ___ ___
, , ——湍流时，法向、切向应力的时均值。
xx yx zx
（相当于层流时的应力值）
___ ___ ___
r xx
,
r yx
,
r zx
——脉动速度产生的法向、切向应力时均值。 （或附加应力时均值）
15
6.涡流粘度与混合长
宗旨：为求解上述方程，必须确立雷诺应力（脉动速度分量） 与时均速度梯度之间的关系。
x
xx ux2
y
yx uyux
z
zx
uzux
——（4）
X ——质量力
x
xx ux2
——法向应力
y
yx uyux
——x方向切向应力（作用面垂直于y）
z
zx
uzux
——x方向切向应力（作用面垂直于z）
10
对上式各项取时均值：
____
__
①
ux ux 0
_____
z
z
z
以上各式代入（4）式有：
0
X
___
xx
___
ux2
___
ux'2
___
yx
__
uy
__
ux
______
u
u' '
yx
x x x y
y
y
___
zx
__
uz
__
ux
______
uz' ux'
z
z
z
12
___
__ __
__ __
或：
u
2 x
uy ux
uz ux
X
x
y
z
__ __
uy
u
' y
,
uz
uz uz'
∴代入连续性方程中，有：
__
__
__
ux
uy
uz
u
' x
u
' y
uz'
0
x y z x y z
6
经过推导整理可得：
ux uy uz 0 x y z
__
__
__
ux uy uz 0
x y z
ux'
u
' y
uz'
0
x y z
时均速度，瞬时速度，脉动速度分量均符合连续性方程。
uz ux X
z
___
xx
x
___
ux'2
x
___
yx
y
______
u
' y
ux'
y
___
zx
z
______
u
u' '
zx
z
（——法向应力） （——切向应力） （——切向应力）
——湍流时的x方向动量衡算方程
13
___ ___ ___
令：
t xx
xx
r xx
___ ___ ___
uuyyuuxx
____ ____
uuzzuuxx
XX
xx
yy
zz
t xx
x
t yx
yt zxz——（5）14
___
t xx ——湍流流动时x方向总法向应力。
___
r xx ——涡流粘性产生的附加法向应力。
___ ___ ___
t xx
,
t yx
,
t zx
——湍流时，总时均法向、切向应力的平均值。
ux，P为瞬时速度及压力，是时间的函数。
3
瞬时参数值等于时均值与脉动值之和。
___
如： ux ux ux'
___
uy
u
y
u
' y
___
uz uz uz'
___
p p p
ux' ,u'y ,uz' ——脉动速度分量;
p ——脉动压强.
根据以上定义，在时间θ内脉动值的平均值应为零，即：
___
7
4.湍流时的微分动量衡算方程
X方向的微分动量衡算方程
Dux X xx yx zx
D
x y z
ux
ux
ux x
uy
ux y
uz
ux z
X
xx
x
yx
y
zx
z
——（1）
又∵
ux uy uz 0
x y z
上式两边同乘 ux，有：
ux
ux x
uy y
uz z
第四章 湍流流动
1
一、关于湍流流动的基本概念
当流体在高速流动时，流体质点不仅在流动方向上运动，而且在 垂直于流动方向的方向上存在着运动。这造成质点的流线和迹线十分 复杂，难以用数学式简单的描述。该流动状态称为湍流。
1、临界雷诺准数
当Re<2000时，流体呈层流，
当Re>4000时，流体呈湍流。
Rec=4000——定义为湍流流动的下限，即临界雷诺准数。
①湍流的统计学说。利用统计学的原理建立雷诺应力与时均速度之间的 关系，这无疑是一条正确的途径，但到目前为止，统计学说还未达到直 接、有效地解决工程实际问题的阶段。 ②半经验半理论的方法。该方法是在理论分析的基础上，先假设建立湍 流时动量传递的机理及模型，然后结合实验结果，建立雷诺应力与时均 速度之间的关系。尽管目前这类方法尚存在某些欠缺，但仍是解决实际 工程问题的一条有效途径。在这方面普兰德（Plandtl）提出的混合长概 念被普遍应用，又称为普兰德动量传递理论。
0
——（2）
8
(1)+(2)得：
ux
2ux
ux x
uy
ux y
ux
uy y
uz
ux z
ux
uz z
X
xx
x
yx
y
zx
z
上式可改写为：
ux
ux2
uyux
uzux X xx yx zx
x
y
z
x y z
——（3）
9
或改写为：
ux X
2
2、时均量与脉动量
在湍流中任一点的流动参数（速度、压力），其大小和方向（速度） 随时间在无规则的变动。严格的讲，湍流中根本不存在稳定状态。通过 取一定时间段中的平均值（时均值）作为其参数值。
X方向上的时均速度定义为：
___
ux
1
0 uxd
时均压力定义为：
__
p
1
pdx
0
__ __
式中： u x，p 为时间θ内的时均值。
u
' x
1
0
u
' x
d
0
4
同理：
___ ___ ___
u'y uz' p' 0
脉动值有正、负之分，其总和为零。
通常所指的稳态流动是指 平均值不随时间变化。
5
3、湍流时的连续性方程
对于不可压缩性流体，其连续性方程为：
ux uy uz 0 x y z
___
___
___
Q ux
ux ux' , uy
16
（１）涡流粘度（涡流运动粘度或表观运动粘度）
波希涅斯克（Boussinesg）按照类似于层流时的牛顿粘性定律， 建立了雷诺应力与时均速度之间的关系。对于平行湍流而言：
t yx
yx
r yx
及
___ ___ ___
t zx
zx
r zx
___
___
r xx
ux'2
___
______
r yx
u
' y
ux'
___
______
r zx
uz' ux'
湍流应力的定义式
上述式中的“负”号表示ux 与uy 的方向相反，即脉动方向相反.
动量衡算方程为：
______
uux2x2
____ ____