第8章 相关分析
- 格式:pdf
- 大小:222.73 KB
- 文档页数:11

第8章 相关分析2. 离散相关与离散序列的卷积运算一样,离散序列的相关运算也可以分为线性相关和循环相关两种类型。
2.1 基本定义线性相互关的计算对应公式(8-1)的离散化形式,计算离散序列][n x 和][n y 的线性互相关,可得:∑+∞-∞=+⋅=i xy n i y i x n r ][][][ (8-6)对有限长度的离散序列][n x ,1,1,0-=L n 、][n y ,1,1,0-=P n ,且二者的长度分别为L 和P 。
那么,有如下公式成立:∑--=+⋅=nP i xy n i y i x n r 10][][][ (8-7)当P n i ≥+时,0][=+n i y ,所以公式(8-7)中的求和上限为n P --1。
因为序列][n r xy 下标n 的取值范围为:11-≤≤-P n M ,所以与线性卷积的长度一样,序列][n x 和][n y 的线性互相关序列的最大长度也是1-+P L 。
与离散Fourier 变换的相关特性对应的是循环相关(或称圆周相关),循环互相关的定义已在第二章中出现过,笔者在下面重新书写一遍。
∑-=+⋅=10])[(][][N i N xy n i y i x n r (8-8)其中,N n i )(+表示)(n i +除以N 的余数,][n r xy 下标n 的取值范围为:2/2/N n N <≤-。
可以利用循环相关来计算两个序列的线性相关,只是要对原有序列进行补零处理。
把长度为L 的序列][n x 和长度为P 的序列][n y 补零后拓展序列长度为N 的新序列][n x 和][n y ,只要满足1-+≥P L N ,两个新序列的循环相关就等同于原有两个序列的线性相关。
与连续函数的互相关函数一样,互相关序列][n r xy 既不是偶序列,也不是奇序列,但满足等式:][][n N r n r yx xy -=。
2.2 快速算法计算两个长度相等的序列的循环相关时,如果直接采用公式(8-8)的定义,计算量是非常大的,尤其在N 较大的情况下。





第8章 相关分析相关分析(Correlations)是研究两个变量间。
或一个变量与多个变量间,或多个变量两两变量间,或两组变量间,或多个变量组与组之间密切程度的一种常用统计学方法。
变量间的密切程度常用相关系数(Correlation Coefficients)或统计量描述。
SAS /Win(v8)系统非编程有如下5种相关量度(Correlation Measure)。
(1)Pearson product-moment correlation ,皮尔逊积矩相关分析。
(2)Spearman coefficients ,斯皮尔曼相关系数s r(3)Cronbach ’coefficient alpha ,克龙巴哈系数α(4)Kendall ’s tan –b coefficient ,肯德尔b τ系数。
(5)Hoeffding ’s D statistic ,霍夫丁D 统计量。
同时将输出变量的简单统计量(Simple Statistics),相关系数(Correlation Coefficients),相应的P 值与图形(P1ots)等。
8-1皮尔逊积矩相关分析[例8-1] 已知5-6岁儿童体检数据的指标为编号(1x ),性别(2x ),月龄(3x ),体重(4x ,kg),身高(5x ,cm),坐高(6x ,cm),胸围(7x ,cm),头围(8x ,cm),左眼视力(9x )与右眼视力(10x ),并已建立SAS 数据集SASUSER.child 。
试对体重(4x )与身高(5x )做皮尔逊(Pearson)相关分析。
(1)进入SAS /Win(V8)系统,单击So1utions->Analysis->Analyst ,进入分析家窗口。
(2)单击File->open By SAS Name->Sasuser->Child->OK ,调入SAS 数据集SASUSER.child(3)单击statistics->Descriptive->correlations ,得到图8-1所示对话框。
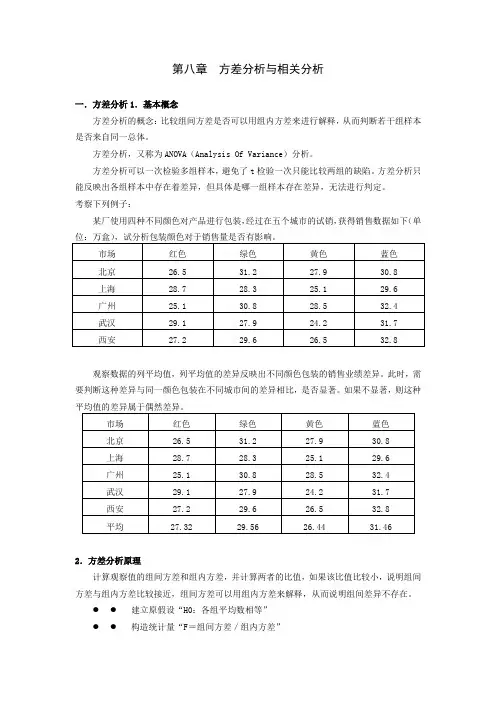
第八章方差分析与相关分析一.方差分析1.基本概念方差分析的概念:比较组间方差是否可以用组内方差来进行解释,从而判断若干组样本是否来自同一总体。
方差分析,又称为ANOVA(Analysis Of Variance)分析。
方差分析可以一次检验多组样本,避免了t检验一次只能比较两组的缺陷。
方差分析只能反映出各组样本中存在着差异,但具体是哪一组样本存在差异,无法进行判定。
考察下列例子:某厂使用四种不同颜色对产品进行包装,经过在五个城市的试销,获得销售数据如下(单观察数据的列平均值,列平均值的差异反映出不同颜色包装的销售业绩差异。
此时,需要判断这种差异与同一颜色包装在不同城市间的差异相比,是否显著。
如果不显著,则这种2.方差分析原理计算观察值的组间方差和组内方差,并计算两者的比值,如果该比值比较小,说明组间方差与组内方差比较接近,组间方差可以用组内方差来解释,从而说明组间差异不存在。
●●建立原假设“H0:各组平均数相等”●●构造统计量“F=组间方差/组内方差”●●在计算组间方差时,使用自由度为(r-1),计算组内方差时,使用自由度为(n-r)。
●●F满足第一自由度为(r-1),第二自由度为(n-r)的F分布。
●●查表,若F值大于0.05临界值,则拒绝原假设,认为各组平均数存在差异。
根据方差计算的原理,生成方差分析表如下:其中:组间离差平方和 SSA (Sum of Squares for factor A) =39.084误差项离差平方和 SSE (Sum of Squares for Error) =76.8455总离差平方和 SST (Sum of Squares for Total)=115.9295P-value值为0.000466,小于0.05,所以拒绝原假设。
3.双因素方差分析观察下列销售数据,欲了解包装方式和销售地区是否对于销售业绩有影响,涉及到双因素的方差分析。
此时需分别计算SSA、SSB与SSE之间的比值是否超过临界值。

![[课件]第八章 直线回归与相关分析PPT](https://uimg.taocdn.com/48735145f5335a8102d2207a.webp)

第八章 相关分析与回归分析习题参考答案一、名词解释函数关系:函数关系亦称确定性关系,是指变量(现象)之间存在的严格确定的依存关系。
在这种关系中,当一个或几个相互联系的变量取一定的数值时,必定有另一个且只有一个变量有确定的值与之对应。
相关关系:是指变量(现象)之间存在着非严格、不确定的依存关系。
在这种关系中,当一个或几个相互联系的变量取一定的数值时,可以有另一变量的若干数值与之相对应。
这种关系不能用完全确定的函数来表示。
相关分析:相关分析主要是研究两个或者两个以上随机变量之间相互依存关系的方向和密切程度的方法,直线相关用相关系数表示,曲线相关用相关指数表示,多元相关用复相关系数表示。
回归分析:回归分析是研究某一随机变量关于另一个(或多个)非随机变量之间数量关系变动趋势的方法。
其目的在于根据已知非随机变量来估计和预测随机变量的总体均值。
单相关:单相关是指仅涉及两个变量的相关关系。
复相关:复相关是指一个变量对两个或者两个以上其他变量的相关关系。
正相关:正相关是指两个变量的变化方向是一致的,当一个变量的值增加(或减少)时,另一变量的值也随之增加(或减少)。
负相关:负相关是指两个变量的变化方向相反,即当一个变量的值增加(或减少)时,另一个变量的值会随之减少(或增加)。
线性相关:如果相关的两个变量对应值在直角坐标系中的散点图近似呈一条直线,则称为线性相关。
非线性相关:如果相关的两个变量对应值在直角坐标系中的散点图近似呈现出某种曲线形式,则为非线性相关。
相关系数:相关系数是衡量变量之间线性相关密切程度及相关方向的统计分析指标。
取值在-1到1之间。
两个变量之间的简单样本相关系数的计算公式为:()()niix x y y r --∑二、单项选择1.B;2.D;3.D;4.C;5.A;6.D 。
三、判断题(正确的打“√”,错误的打“×”) 1.×; 2.×; 3.√; 4.×; 5.×; 6.×; 7.×; 8.√. 四、简答题1、什么是相关关系?相关关系与函数关系有什么区别?答:相关关系,是指变量(现象)之间存在着非严格、不确定的依存关系。

第 8 章 相关分析8.1 相关分析的理论与方法社会经济现象总体数量上所存在的依存关系有两种不同的类型,一种是函数关系,一种是相关关系。
函数关系是指当某一变量的数值确定之后,另一个变量的数值也完全随之而确定了。
例如电路中的欧姆定律表述了电压、电阻和电流之间的关系:电压=电流×电阻,若已知其中两个变量的值,则另一个变量的值就被唯一确定了。
相关关系是不完全确定的随机关系。
在相关关系的情况下,当一个或几个相互联系的变量取一定的值时,与之相应的另一变量的值虽然不确定,但它仍然按某种规律在一定的范围内变化。
例如,商品需求与商品价格之间的关系、投资额与国民收入之间的关系、得病率与性别的关系等等。
按照数据度量尺度的不同,相关分析的方法也不同。
连续变量之间的相关性常用Pearson 简单相关系数来测定;定序变量的相关性常用Spearman 秩相关系数或Kendall 秩相关系数来测定;而定类变量的相关分析则要使用列联表分析方法。
8.1.1 连续变量的相关分析1. Pearson 简单相关系数对于像投资额、国民收入等连续变量之间的相关性分析常用Pearson 简单相关系数来测定,其基本公式如下:2xyx yr σσσ=其中,2xy σ 为变量x 和的协方差,y x σ和y σ分别为变量x 和的标准差。
y Pearson 简单相关系数有如下的特征:r1r ≤ ,r 越大表示两变量相关性越强,r 越小表示两变量相关性越弱 0r =时,表示两变量不存在线性相关关系 1r =时,表示两变量完全正相关1r =−时,表示两变量完全负相关2. Pearson 简单相关系数的检验在实际分析中,相关系数大都是利用样本数据计算的,因而带有一定的随机性,因此也需要对相关关系的显著性进行检验,该检验的原假设为两总体相关系数等于0。
数学上可以证明,在原假设得到满足的条件下,有下面的t 统计量:t =该统计量服从自由度为的t 分布。
2n −8.1.2 定序变量的相关分析对于定序变量的相关性分析,例如分析勤奋程度与成就高低的关系、信用等级与贷款收回情况的关系等等都不能用简单相关系数来测定,而要用秩相关的非参数方法来实现,即不使用变量的原始数据,而使用原始数据的秩来计算相关系数。
1. Spearman 秩相关系数假设有容量为n 的由x 和两个变量构成的随机样本。
分别计算每个观测关于变量y x 和的秩变量和,用y i u i v (1,)=L ,2i n i i d u v i =−表示第i 个样本对应于两变量的秩之差,则Spearman 秩相关系数的公式如下:)1(61212−−=∑=n n d r ni i s与Pearson 简单相关系数一样,Spearman 秩相关系数的取值也处于-1和1之间。
显然,和之间的差别越大,则就越大。
若所有的和都相等,则,。
i u i v 21n i i d =∑i u i v 210ni i d ==∑1s r =计算出Spearman 秩相关系数后,要对该系数进行检验,此时的原假设为:两变量不相关。
在满足原假设的前提下,若是小样本,则服从Spearman 分布;在大样本下,统计量s r sr z r =近似服从标准正态分布。
2. Kendall 秩相关系数Kendall 秩相关系数与Spearman 秩相关系数类似,都是利用变量的秩进行计算,只是计算方式不同。
首先计算每个观测关于变量x 和的秩变量u 和v ,将n 个观测按变量y x 的升序排序,则n 个观测关于变量x 和的秩如下:y x 的秩变量u : 1 2 …… ny 的秩变量: ……v 1v 2v n v 设在的后面有1v 1R 个秩大于,在的后面有1v 2v 2R 个秩大于,……,在后面有2v 1n v −1n R −个秩大于,令1n v −12n 1R R R R −=+++L显然,变量x 和y 相关性越强,则R 越大。
Kendall 秩相关系数按如下公式求得:41(1)k Rr n n =−−同样,Kendall 秩相关系数的绝对值不超过1。
为了说清楚变量之间具有联系的理由,也应对Kendall 秩相关系数进行显著性检验。
此时的原假设同样为两变量不相关。
在满足原假设的前提下,若是小样本,则服从Kendall 分布;在大样本下,统计量kr z =近似服从标准正态分布。
8.1.3 定类变量的相关分析在7.2节我们曾介绍了利用2χ统计量对单一随机样本的分布进行检验的方法。
卡方检验还有一个重要的用途就是对离散变量的相关性进行检验,这种方法有时也叫作“列联表分析”。
列联表是多行多列纵横交错所形成的一个表体。
我们以例子说明列联表的形式以及如何将定类变量的相关性检验化为列联表并进行检验分析的程序。
抽样调查某地区500名待业人员,这些人员中文化程度为高中及以上的有104人(男44人),初中的有96人(男36人),小学及以下的有300人(男140人)。
试检验此调查结果能否说明待业人员中的文化程度与性别是相互独立的。
根据调查结果,我们可将数据整理成列联表:表 8-1 待业人员文化程度与性别列联表列联表的单元格中,上面的数字给出样本关于两变量的联合观察频数;下面括号内的数值为对应的联合期望频数,计算方法为:..i jij n n E n×=其中,ij E 为第一个变量取第个取值,第二个变量取第i j 个变量时的联合观察频数,为第i 行的观察频数之和,.i n .j n 为第j 列的观察频数之和,为样本容量。
n 例如,性别为男且文化程度为高中及以上所对应的期望频数为:1122010446500E ×==,其它各个单元格对应的期望频数也按同样方法计算得到。
统计量来检验两变量的相关性。
在得出对应的期望频数后,我们就可以应用Pearson 2χ该检验的原假设为:两变量相互独立。
构造的统计量为:22(ij ij E χ11s ti j ijf E ==−=∑∑其中,和分别为两个离散变量取值的个数,s t ij f 为第一个变量取第个取值,第二个变量取第i j 个变量时的联合期望频数。
在原假设成立的条件下,该统计量服从一个自由度为(1)(s t −−的1)2χ分布。
8.2 连续变量相关分析实例8.2.1 SPSS 操作步骤,常常利用资产收益率、净资产收益率、每股净收益和托宾Q 值四个指标来衡量公司经营绩效。
本节将利用SPSS 对这四个指标的相关性进行检验。
四个变量都是连续在上市公司财务分析中1. 选择菜单项Analyze →Correlate →Bivariate ,打开Bivariate Correlations 对话框,如图 8-1。
将待分析的四个衡量公司绩效的指标移入右边的Variables 列表框中。
2. 在Correlation Coefficients 选项栏中选择适当的相关系数。
三个选项分别是Pearson 简单相关系数、Kendall 秩相关系数和Spearman 秩相关系数。
本例中待分析的变量都是连续型数据,因此应该选择Pearson 简单相关系数,但为了便于比较,这里将两个非参数相关系数也选上。
3. 在Test of Significance 选项栏中选择在相关系数检验时使用双侧检验(Two-Tailed )还是单侧检验(One-Tailed )。
4. 如果选中Flag significant correlations ,则在相关系数检验中用星号标注通过显著性检验的相关系数。
图 8-1 Bivariate Correlations 对话框5. 单击Options 按钮,打开。
Statistics 选项栏用于选择是否待分的样本协差阵(Means and ns ),这是多元统计分析中Options 子对话框,如图 8-2在结果输出窗口中输出析变量standard deviations)和样本叉积离差阵(Cross-product deviatio两个这两个变量中带有缺失值的观测删除,即如果一个观测在正非常重要的样本统计量矩阵。
Missing Values 选项栏用于设置缺失值的处理方法。
Exclude case pairwise 表示在计算两个变量的协方差或相关系数时,只把在进行相关系数计算的变量中没有缺失值,则即使其它变量中有缺失值,也不影响它参与计算;Exclude case listwise 表示如果某个观测的所有分析变量中只要由一个带有缺失值,则这个观测就不参与分析。
图 8-2 Options 子对话框6. 在主对话框中单击OK 按钮,执行命令。
8.2.相关系数、相关检验t 统计量对应的2 实例结果分析表 8-2给出了Pearson 简单p 值、叉积离差阵和协差阵。
相关系数右上角有两个星号表示相关系数在0.01的显著性水平下显著。
从表中可以看出,每股在收益、净资产收益率和总资产收益率三个指标之间的相关系数都0.8以上,对应的p 值都接近于0,表示三个指标具有较强的正相关关系,而托宾Q 值与其他三个变量之间的相关性较弱。
表 8-2 Pearson 简单相关分析表 8-3给出Kendall秩相关系数和Spearman秩相关系数两种非参数相关分析结果。
从表中可以看出,使用非参数方法得出了与Pearson简单相关分析基本一致的结果。
表 8-3 Kendall秩相关分析和Spearman秩相关分析8.3 离散变量相关分析实例8.3.1 SPSS 操作步骤离散变量相关分析常用的方法是列联表分析法。
以补钙产品市场调查数据为例。
1. 选择菜单项Analyze →Descriptive Statistics →Crosstabs ,打开Crosstabs 对话框,如图 8-3。
将两个需要分析相关性的离散变量分别移入Rows 列表框和Columns 列表框。
如果要分析多于两个变量的相关性,则可以将其余变量移入Layer 列表框中,则SPSS 将构筑多维列联表来分析多个变量之间的相关性。
这里我们首先分析消费者对补钙产品的购买欲望(g3)是否与性别(gender )显著相关,所以,将这两个变量分别移入Rows 列表框和Columns 列表框。
2. 选择Display clustered bar charts 复选框,绘制交叉分组下的频数分布条形图,通过该图形可以直观地观察两变量的相关性。
,而仅给出相关分析的检验统计量。
这里不选择该选项xtract 按钮的用途参考7.2节。
3. Suppress tables 表示不输出列联表。
4. E图 8-3 Crosstabs对话框5. 单击Statistics按钮,打开Statistics子对话框,如图 8-4。
该对话框用于指定相关分析的方法以及使用的统计量。