利用SPSS进行相关分析第八章
- 格式:ppt
- 大小:1.78 MB
- 文档页数:56

第8章SPSS的相关分析学习目标:1.明确相关关系的含义以及相关分析的主要目标。
2.掌握散点图的含义,熟练掌握绘制散点图的具体操作。
3.理解简单相关系数、Spearman相关系数、Kendall相关系数的基本原理,熟练掌握计算各种相关系数的具体操作,能够读懂分析结果。
4.理解偏相关系分析的主要目标以及与相关分析之间的关系,熟练掌握偏相关分析的具体操作,能够读懂分析结果。
8.1 相关分析相关分析是分析客观事物之间关系的数量分析方法,明确客观事物之间有怎样的关系对理解和运用相关分析是极为重要的。
客观事物之间的关系大致可归纳为两大类关系,它们是函数关系和统计关系。
相关分析是用来分析事物之间统计关系的方法。
所谓函数关系指的是两事物之间的一种一一对应的关系,即荡一个变量x取一定值时,另一变量y可以依确定的函数取唯一确定的值。
例如,商品的销售额与销售量之间的关系,在单价确定时,给出销售量可以唯一地确定出销售额,销售额与销售量之间是一一对应的关系,且这个关系可以被y=Ρx(y表示销售额,Ρ表示单价,x表示销售量)这个数学函数精确地描述出来。
客观世界中这样的函数关系有很多,如圆面积和圆半径、出租车费和行程公里数之间的关系等。
另一类普遍存在的关系是统计关系。
统计关系指的是两事物之间的一种非一一对应的关系,即当一个变量x取一定值时,另一变量y无法依确定的函数取唯一确定的值。
例如,家庭收入和支出、子女身高和父母身高之间的关系等。
这些事物之间存在一定的关系,但这些关系却不能像函数关系那样可用一个确定的数字函数描述,且当一个变量x取一定值时,另一变量y的值可能有若干个。
统计关系可再进一步划分为线性相关和非线性相关关系。
线性相关又可分为正线性相关和负线性相关。
正线性相关关系指两个变量线性的相随变动方向相同,而负线性相关关系指两个变量线性的相随变动方向相反。
事物之间的函数关系比较容易分析和测度,而事物之间的统计关系却不像函数关系那样直接,但确实普遍存在,并且有的关系强,有的关系弱,程度各有差异。
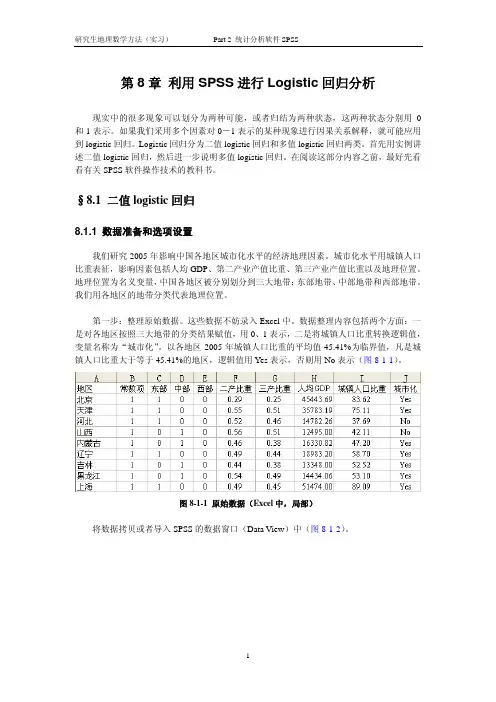


SPSS统计分析第八章聚类分析与判别分析聚类分析与判别分析是SPSS统计分析中非常重要的两个方法。
聚类分析是寻找数据之间的相似性,将相似的数据划分为一个簇,从而实现对数据的归类和分组。
判别分析则是寻找数据之间的差异性,帮助我们理解不同因素对于数据的影响程度,从而实现对数据的分类预测。
首先,我们来介绍聚类分析。
聚类分析是根据数据之间的相似性进行归类的一种方法,通过度量数据之间的相似性,将相似的数据归为一类。
它在寻找数据内在组织结构和特点上具有很大的作用。
在SPSS中进行聚类分析的步骤如下:1.载入数据集:在SPSS软件中,选择"文件"->"打开"->"数据",选择需要进行聚类分析的数据集。
2.选择聚类变量:在"分析"->"分类"->"聚类"中,选择需要进行聚类分析的变量。
可以选择一个或多个变量作为聚类变量,决定了聚类的维度。
3.设置聚类参数:在设置参数的对话框中,可以选择使用不同的距离测度和聚类算法。
距离测度可以选择欧氏距离、曼哈顿距离、切比雪夫距离等,而聚类算法可以选择层次聚类、K均值聚类等。
根据具体的数据特点,选择合适的参数。
4.进行聚类分析:点击"确定"按钮,SPSS会自动进行聚类分析,并生成聚类的结果。
聚类结果可以通过树状图、散点图等形式展示,便于我们对数据的理解和分析。
接下来,我们来介绍判别分析。
判别分析是一种通过建立数学模型,根据不同的预测变量对数据进行分类和预测的方法。
判别分析可以帮助我们理解不同因素对于数据分类的重要性,从而进行有针对性的分析和预测。
在SPSS中进行判别分析的步骤如下:1.载入数据集:同样,在SPSS软件中,选择"文件"->"打开"->"数据",选择需要进行判别分析的数据集。


SPSS教程第八课:相关分析任何事物的存在都不是孤立的,而是相互联系、相互制约的。
在医学领域中,身高与体重、体温与脉搏、年龄与血压等都存在一定的联系。
说明客观事物相互间关系的密切程度并用适当的统计指标表示出来,这个过程就是相关分析。
值得注意,事物之间有相关,不一定是因果关系,也可能仅是伴随关系。
但如果事物之间有因果关系,则两者必然相关。
SPSS的相关分析是借助于Statistics(新版为analysis)菜单的Correlate选项完成的。
第一节 Bivariate过程7.1.1 主要功能调用此过程可对变量进行相关关系的分析,计算有关的统计指标,以判断变量之间相互关系的密切程度。
调用该过程命令时允许同时输入两变量或两个以上变量,但系统输出的是变量间两两相关的相关系数。
7.1.2 实例操作[例7-1]某地区10名健康儿童头发和全血中的硒含量(1000ppm)如下,试作发硒与血硒的相关分析。
编号发硒血硒1 74 132 66 103 88 134 69 115 91 166 73 97 66 78 96 149 58 510 73 107.1.2.1 数据准备激活数据管理窗口,定义变量名:发硒为X,血硒为Y,按顺序输入相应数值,建立数据库(图7.1)。
7.1.2.2 统计分析激活Statistics菜单选Correlate中的Bivariate...命令项,弹出BivariateCorrelation对话框(图7.2)。
在对话框左侧的变量列表中选x、y,点击Ø钮使之进入Variables框;再在CorrelationCoefficients框中选择相关系数的类型,共有三种:Pearson为通常所指的相关系数(r),Kendell’stau-b为非参数资料的相关系数,Spearman为非正态分布资料的Pearson相关系数替代值,本例选用Pearson项;在Test ofSignificance框中可选相关系数的单侧(One-tailed)或双侧(Two-tailed)检验,本例选双侧检验。

![[课件]第八章SPSS的相关分析和线性相关分析PPT](https://uimg.taocdn.com/76ebd16e2b160b4e767fcfdd.webp)

第八章SPSS的相关分析和线性相关分析在统计学中,相关分析是用来研究两个或多个变量之间关系的一种方法。
SPSS(Statistical Package for the Social Sciences)是一款常用的统计软件,可用于进行相关分析和线性相关分析。
本章将介绍如何使用SPSS进行相关分析和线性相关分析,以及如何解释分析结果。
一、相关分析相关分析是一种用于研究变量之间关系的统计方法。
通过相关分析可以确定两个或多个变量之间的关联程度,以及这种关联程度的方向(正相关或负相关)。
在SPSS中进行相关分析的步骤如下:1.打开SPSS软件,选择“文件”>“打开”>“数据”,选择要进行分析的数据文件,点击“打开”。
2.在菜单栏中选择“分析”>“相关”>“双变量”或“多变量”。
3. 在弹出的对话框中,将变量移动到“变量”框中。
可以选择自定义相关性系数的类型,如Pearson相关系数、Spearman相关系数等。
4.点击“OK”进行相关分析。
5.SPSS将生成一个相关矩阵和一个相关系数表格,展示了变量之间的关联程度。
在进行相关分析时,需要注意以下几点:1.相关系数的取值范围为-1到1,-1表示完全负相关,1表示完全正相关,0表示没有相关性。
2.根据相关系数的取值大小可以判断变量之间的关联程度,一般认为相关系数大于0.7为强相关,0.3到0.7为中等相关,小于0.3为弱相关。
3.相关分析只能判断变量之间是否存在关系,不能确定因果关系。
线性相关分析是一种用于研究两个变量之间线性关系的统计方法。
通过线性相关分析可以确定两个连续变量之间的关联程度,以及这种关联程度的方向(正相关或负相关)。
在SPSS中进行线性相关分析的步骤如下:1.打开SPSS软件,选择“文件”>“打开”>“数据”,选择要进行分析的数据文件,点击“打开”。
2.在菜单栏中选择“分析”>“相关”>“双变量”。