第八章典型相关分析

第8章 相关分析6. 最大互相关方法(MCC)除了上面介绍的各种相关分析方法，还存在一种称为最大互相关方法(MCC ：Maximum Cross Correlation)的算法。

MCC 算法是非常传统的算法，在许多文献中都有提及，其特性和缺陷也在许多文献中有所讨论。

MCC 算法是一种基于互相关系数，取决于两张图片相似性的模板匹配算法，国内外研究人员在极区海冰漂移分析和海洋表面流场分析中经常使用该方法，因为前面的举例中笔者已经列举了极区海冰漂移分析结果，笔者后面列举的算例中提供MCC 算法在海表流场中的遥感分析应用。

6.1 MCC 原理MCC 计算过程可用图8-14表示。

A ：源模块B ：诊断窗口C ：位移矢量图8-14 MCC 计算过程简略图解 假定),(1n j m i I ++，2/2/M m M <≤-、2/2/N n N <≤-表示图8-14-A 中中心位置在(i ,j )、形状大小为M ×N 的图像块每一个点的数值(如图像灰度值)，对应的),(2n l j m k i I ++++表示图8-14-B 中中心位置在(i+k ,j+l )、形状大小为M ×N 的图像块每一个点的数值。

源模块和目标模块之间的相似性可以用如下公式(8-34)的互相关系数量化表示出来：∑∑∑∑∑∑--=--=--=--=--=--=++-++++⨯-++++-++++⨯-++=1221222221221222111221222211)],(),([)],(),([)],(),([)],(),([),(M M m N N n M M m N N n M M m N N n l j k i I n l j m k i Ij i I n j m i I l j k i I n l j m k i I j i I n j m i I l k r (8-34) 上式中，),(1j i I 表示图8-14-A 中中心位置在(i ,j )的选定的源模块范围的平均值，),(2l j k i I ++表示图8-14-B 中中心位置在(i+k ,j+l )的选定的目标模块范围的平均值。

第8章 相关分析相关分析(Correlations)是研究两个变量间。

或一个变量与多个变量间，或多个变量两两变量间，或两组变量间，或多个变量组与组之间密切程度的一种常用统计学方法。

变量间的密切程度常用相关系数(Correlation Coefficients)或统计量描述。

SAS ／Win(v8)系统非编程有如下5种相关量度(Correlation Measure)。

(1)Pearson product-moment correlation ，皮尔逊积矩相关分析。

(2)Spearman coefficients ，斯皮尔曼相关系数s r(3)Cronbach ’coefficient alpha ，克龙巴哈系数α(4)Kendall ’s tan –b coefficient ，肯德尔b τ系数。

(5)Hoeffding ’s D statistic ，霍夫丁D 统计量。

同时将输出变量的简单统计量(Simple Statistics)，相关系数(Correlation Coefficients)，相应的P 值与图形(P1ots)等。

8-1皮尔逊积矩相关分析[例8-1] 已知5-6岁儿童体检数据的指标为编号(1x )，性别(2x )，月龄(3x )，体重(4x ，kg)，身高(5x ，cm)，坐高(6x ，cm)，胸围(7x ，cm)，头围(8x ，cm)，左眼视力(9x )与右眼视力(10x )，并已建立SAS 数据集SASUSER.child 。

试对体重(4x )与身高(5x )做皮尔逊(Pearson)相关分析。

(1)进入SAS ／Win(V8)系统，单击So1utions->Analysis->Analyst ，进入分析家窗口。

(2)单击File->open By SAS Name->Sasuser->Child->OK ，调入SAS 数据集SASUSER.child(3)单击statistics->Descriptive->correlations ，得到图8-1所示对话框。

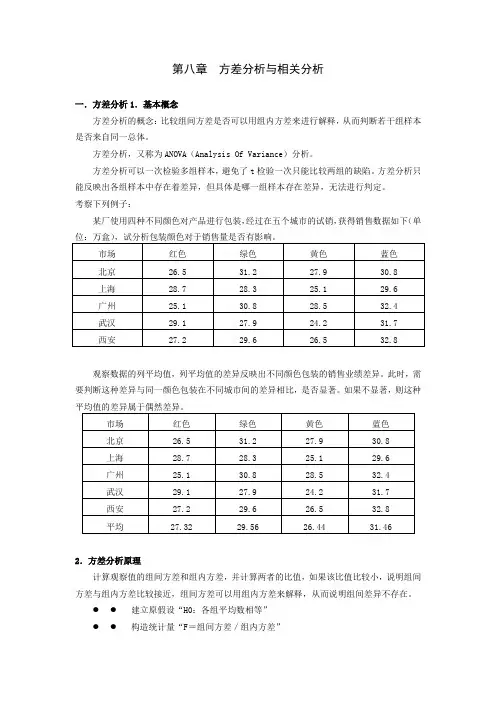
第八章方差分析与相关分析一．方差分析1．基本概念方差分析的概念：比较组间方差是否可以用组内方差来进行解释，从而判断若干组样本是否来自同一总体。

方差分析，又称为ANOVA（Analysis Of Variance）分析。

方差分析可以一次检验多组样本，避免了t检验一次只能比较两组的缺陷。

方差分析只能反映出各组样本中存在着差异，但具体是哪一组样本存在差异，无法进行判定。

考察下列例子：某厂使用四种不同颜色对产品进行包装，经过在五个城市的试销，获得销售数据如下（单观察数据的列平均值，列平均值的差异反映出不同颜色包装的销售业绩差异。

此时，需要判断这种差异与同一颜色包装在不同城市间的差异相比，是否显著。

如果不显著，则这种2．方差分析原理计算观察值的组间方差和组内方差，并计算两者的比值，如果该比值比较小，说明组间方差与组内方差比较接近，组间方差可以用组内方差来解释，从而说明组间差异不存在。

●●建立原假设“H0：各组平均数相等”●●构造统计量“F＝组间方差／组内方差”●●在计算组间方差时，使用自由度为（r-1），计算组内方差时，使用自由度为（n-r）。

●●F满足第一自由度为（r-1），第二自由度为（n-r）的F分布。

●●查表，若F值大于0.05临界值，则拒绝原假设，认为各组平均数存在差异。

根据方差计算的原理，生成方差分析表如下：其中：组间离差平方和 SSA (Sum of Squares for factor A) ＝39.084误差项离差平方和 SSE (Sum of Squares for Error) ＝76.8455总离差平方和 SST (Sum of Squares for Total)＝115.9295P-value值为0.000466，小于0.05，所以拒绝原假设。

3．双因素方差分析观察下列销售数据，欲了解包装方式和销售地区是否对于销售业绩有影响，涉及到双因素的方差分析。

此时需分别计算SSA、SSB与SSE之间的比值是否超过临界值。

第八章 相关分析与回归分析习题参考答案一、名词解释函数关系：函数关系亦称确定性关系，是指变量（现象）之间存在的严格确定的依存关系。

在这种关系中，当一个或几个相互联系的变量取一定的数值时，必定有另一个且只有一个变量有确定的值与之对应。

相关关系：是指变量（现象）之间存在着非严格、不确定的依存关系。

在这种关系中，当一个或几个相互联系的变量取一定的数值时，可以有另一变量的若干数值与之相对应。

这种关系不能用完全确定的函数来表示。

相关分析：相关分析主要是研究两个或者两个以上随机变量之间相互依存关系的方向和密切程度的方法，直线相关用相关系数表示，曲线相关用相关指数表示，多元相关用复相关系数表示。

回归分析：回归分析是研究某一随机变量关于另一个（或多个）非随机变量之间数量关系变动趋势的方法。

其目的在于根据已知非随机变量来估计和预测随机变量的总体均值。

单相关：单相关是指仅涉及两个变量的相关关系。

复相关：复相关是指一个变量对两个或者两个以上其他变量的相关关系。

正相关：正相关是指两个变量的变化方向是一致的，当一个变量的值增加（或减少）时，另一变量的值也随之增加（或减少）。

负相关：负相关是指两个变量的变化方向相反，即当一个变量的值增加（或减少）时，另一个变量的值会随之减少（或增加）。

线性相关：如果相关的两个变量对应值在直角坐标系中的散点图近似呈一条直线，则称为线性相关。

非线性相关：如果相关的两个变量对应值在直角坐标系中的散点图近似呈现出某种曲线形式，则为非线性相关。

相关系数：相关系数是衡量变量之间线性相关密切程度及相关方向的统计分析指标。

取值在-1到1之间。

两个变量之间的简单样本相关系数的计算公式为：()()niix x y y r --∑二、单项选择1.B;2.D;3.D;4.C;5.A;6.D 。

三、判断题（正确的打“√”，错误的打“×”） 1.×; 2.×; 3.√; 4.×; 5.×; 6.×; 7.×; 8.√. 四、简答题1、什么是相关关系？相关关系与函数关系有什么区别？答：相关关系，是指变量（现象）之间存在着非严格、不确定的依存关系。

第8章 典型相关分析典型相关分析是用来描述两组随机变量（两个随机向量）间关系的统计分析方法。

两组随机向量，各含有许多随机变量，能否用少量随机变量来描述其相关性？例如为了研究饲料与荤菜价格的关系，统计若干年玉米、大豆、稻子、麦子、鱼粉以及猪肉、牛肉、羊肉、鸡肉、鸡蛋、鸭肉、鸭蛋的价格，分析饲料与荤菜价格的关系时，发现单独一种饲料和单独一种肉蛋禽价格关系并不密切(由显著性检验可见)，但饲料的某种综合价格则与肉蛋禽综合价格的关系很密切。

把饲料价格看成一组随机变量，肉蛋禽价格看成另一组随机变量，找这两组随机变量的线性组合，使之相关系数平方最大，从而分析两组随机变量间的关系，判定这两组随机变量是否有关联，这就是典型相关分析。

8.1 典型相关分析数学模型设随机向量)',...(1p x x X =与)',...(1p y y Y =的方差yy xx ∑∑,存在，协方差为xy Y X ∑=),cov(。

b a ,为常数向量。

则1/2(',')'/('')xy xx yy corr a X b Y a b a ab b =∑∑∑，为了计算确定性，限制,1')'(=∑=a a X a D xx 1')'(=∑=b b Y b D yy 。

定义8.1 设11,b b a a ==在条件：,1')'(=∑=a a X a D xx 1')'(=∑=b b Y b D yy下使co v(',')a X b Y 大，则称Y b w X a v ','1111==为第一对典型相关变量，c o v(',')a Xb Y 称为第一典型相关系数。

由定义可见，11,w v 尽可能多地反映原来p 对随机变量相关的信息。

第一对典型相关变量往往不能完全反映随机向量间的关系，必须建立其它典型相关变量,它应当最能反映随机向量间的关系，但是它应当与第一对典型相关变量不相关（不包含第一对典型相关变量的信息）。

第八章相关分析一、单项选择⒈当自变量按必然数量转变时，因变量也相应随之而等量转变，这时两个变量之间存在着（ ）①直线相关关系；②曲线相关关系；③负相关关系；④正相关关系。

⒉当变量ｘ值增加时，变量ｙ值随之下降，那ｘ和ｙ两个变量之间存在着（ ） ①正相关关系；②负相关关系；③曲线相关关系；④直线相关关系。

⒊假设变量ｘ值减少，而变量ｙ值却增加，那么变量ｘ与变量ｙ之间存在着（ ）①直线相关关系；②正相关关系；③曲线相关关系；④负相关关系。

⒋圆的面积与半径间存在着（ ）①相关关系；②因果关系；③函数关系；④比较关系。

⒌若是变量ｘ和变量ｙ之间的相关系数为－１，这说明两变量之间是（ ） ①高度相关关系；②完全相关关系；③低度相关关系；④完全不相关。

⒍相关分析和回归分析相较，对变量的性质要求是不同的。

回归分析中要求（ ）①自变量是给定的，因变量是随机的； ②两个变量都是非随机的； ③两个变量都是随机的； ④以上三个都不对。

⒎若是变量ｘ和变量ｙ之间的相关系数为１，那么说明两个变量之间是（ ） ①完全不相关；②高度相关关系；③完全相关关系；④低度相关关系。

⒏相关关系中，两个变量的关系是对等的，从而变量ｘ对变量ｙ的相关，同变量ｙ对变量ｘ的相关（ ）①完全不同；②有联系但不一样；③是同一问题；④不必然相同。

⒐已知某工厂甲产品产量和生产本钱有直接关系，在这条直线上，当产量为1000时，其生产本钱为30000元，其中不随产量转变的本钱为6000元，那么本钱总额对产量的回归方程是（ ）①ｙ=6000+24x ；②y=6+；③y=24000+6x ；④y=24+6000x 。

⒑已知)(∑-x x 2是)(∑-y y 2的两倍，并已知)(∑-x x ·)(y y -是)(∑-y y 2的倍，那么相关系数ｒ为（ ） ①不能计算；②；③22.1；④22.1。

⒒在相关分析中，要求相关的两个变量（ ） ①都是随机变量； ②都不是随机变量；③其中因变量是随机变量； ④其中自变量是随机变量。