运动微分方程

质点运动微分方程的初始条件
初始条件，又称初始条件问题，是指求解给定微分方程时必须满足的一组条件。

初始条件通常包括了物体的初始位置和速度，并由物理定律所确定。

在质点运动微分方程中，初始条件一般有：
1.位置初值：指定质点初始位置，一般由坐标系确定，如
x0=Ri(t=0)；
2.速度初值：指定质点初始速度，一般由分数阶导数确定，如
v0=Ri′(t=0)；
3.加速度初值：指定质点初始加速度，一般由二阶以上导数确定，如a0=Ri″(t=0)。

此外，还需要指定时间t的初值，一般由实验条件或特定问题确定。

运动微分方程和运动方程1. 引言运动微分方程和运动方程是描述物体运动的重要工具，它们在物理学、工程学和其他科学领域中得到广泛应用。

本文将介绍运动微分方程和运动方程的基本概念、应用领域以及解决问题的方法。

2. 运动微分方程运动微分方程是描述物体运动的微分方程。

它可以用来表示物体在一定时间内的位置、速度和加速度之间的关系。

在一维情况下，运动微分方程可以表示为：d2xdt2=a(t)其中，x(t)是物体在时刻t的位置，a(t)是物体在时刻t的加速度。

这个方程可以通过积分求解，得到物体的位置函数x(t)。

在二维和三维情况下，运动微分方程可以表示为：d2xdt2=a x(t)d2ydt2=a y(t)d2zdt2=a z(t)其中，x(t)、y(t)和z(t)分别是物体在时刻t的x、y和z坐标，a x(t)、a y(t)和a z(t)分别是物体在时刻t的x、y和z方向的加速度。

这个方程组可以通过积分求解，得到物体的位置函数x(t)、y(t)和z(t)。

3. 运动方程运动方程是描述物体运动的方程。

它可以用来表示物体在一定时间内的位置、速度和加速度之间的关系。

在一维情况下，运动方程可以表示为：x(t)=x0+v0t+12at2其中，x(t)是物体在时刻t的位置，x0是物体在时刻t=0的初始位置，v0是物体在时刻t=0的初始速度，a是物体在时刻t的加速度。

这个方程可以通过积分求解，得到物体的位置函数x(t)。

在二维和三维情况下，运动方程可以表示为：x(t)=x0+v0x t+12a x t2y(t)=y0+v0y t+12a y t2z(t)=z0+v0z t+12a z t2其中，x(t)、y(t)和z(t)分别是物体在时刻t的x、y和z坐标，x0、y0和z0分别是物体在时刻t=0的初始位置，v0x、v0y和v0z分别是物体在时刻t=0的初始速度，a x、a y和a z分别是物体在时刻t的x、y和z方向的加速度。

质点运动微分方程质点运动微分方程是描述物体运动的基本方程。

它是基于牛顿第二定律推导出来的。

在强加一个力的作用下，质点的加速度与力成正比，其方向与力的方向一致。

通过利用微积分学中的知识，我们可以得到质点运动的微分方程。

质点运动微分方程在物理学和工程学中有着广泛的应用。

下面，我将详细介绍质点运动微分方程的原理和应用。

首先，让我们来看看质点运动微分方程的原理。

运动状态可以用位置矢量r(t)来描述。

在t时刻，质点所处的位置矢量为r(t)。

我们假设质点受到一个力F(t)的作用力，则根据牛顿第二定律，有以下方程：F(t) = ma(t)其中，m为质量，a(t)为加速度。

根据物理学中的定义，加速度a(t)等于位置矢量r(t)对时间t的二阶导数。

因此，我们可以用r(t)对t的二阶导数来表示质点的加速度a(t)，如下所示：a(t) = d^2r(t)/dt^2将上述公式代入牛顿第二定律，得到质点运动微分方程：F(t) = m(d^2r(t)/dt^2)质点运动微分方程表明了力F(t)与位置矢量r(t)之间的关系。

这个方程的意义在于，给定一定的力，我们可以通过解方程来确定质点的运动状态。

因此，在物理学和工程学中，质点运动微分方程是解决运动问题的一个基本工具。

接下来，让我们来看看质点运动微分方程的应用。

质点运动微分方程在物理学和工程学中有着广泛的应用。

例如，在机械工程学中，我们可以用微分方程来描述物体的运动状态。

机械系统通常受到多个力的作用，因此需要解决多个微分方程，以确定系统的运动状态。

在电气工程学中，质点运动微分方程可以用来描述电路中电荷的运动状态。

在控制论中，微分方程可以用来描述物理系统的动态行为，并进一步设计控制算法。

总之，质点运动微分方程是描述物体运动的基本方程。

它可以用来解决物理学和工程学中的一些运动问题，例如机械系统的运动状态、电路中电荷的运动状态和控制系统的动态行为。

因此，熟练掌握质点运动微分方程，对于物理学和工程学的学习和应用非常重要。

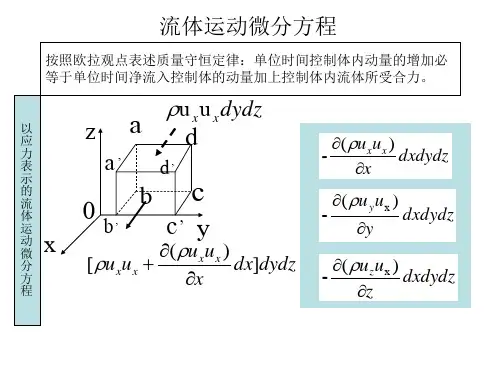
§2-3 运动(yùndòng)微分方程的求解1.求解步骤1)确定分析对象（隔离体）2)作受力分析（施力物、超距力、接触力），画隔离体图3)建立合适坐标系，写出方程解析式并给出初始位置、速度4)给出二阶常微分方程组的数字解5)阐明结果的物理含意与实质作用力为时间、位置、速度的函数；若力只是其中某一项的函数，则问题可加以简化。

2.常力作用下质点的运动〖例2-1〗求质点m在常力作用下的运动。

已知t=0时初位置和初速度分别为。

解：3.力只是时间的函数〖例2-2〗求自由电子-e在沿x轴的电场中的运动。

已知t=0时。

解：4.力只是速度的函数〖例2-3〗求在阻力正比于速度即的介质中抛物体的运动。

已知t=0时。

解：消去t得轨道方程为若阻力很小或距离很短（开始运动），即时，有轨道开始时接近抛物线，x趋于时y趋于无穷大，即为竖直直线。

5.力只是坐标的函数〖例2-4〗求做一维振动的弹性系数为k的弹簧振子的运动。

解：二维振动与利萨如图形。

6.复杂情况力为时间、坐标、速度的函数一维：（受迫振动）如LRC电路：为二阶常系数线性常微分方程，可用数值计算。

7.例题〖例2-5〗P39例1〖例2-6〗P41例3§2-4 加速(jiā sù)平动非惯性系动力学1.问题的提出在惯性系S中成立，在动系S’中是否成立？作加速平动的参照系为非惯性系。

2.改进的牛顿定律引入惯性力后牛顿定律仍成立。

3.讨论？为什么选择非惯性系：方便？惯性力与普通力的差别惯性力只是一种记号，它无施力物体，也无反作用力4.例题〖例2-7〗P44例质点运动(yùndòng)微分方程小结1.运动微分方程2.运动微分方程的解析式或3.理想光滑线约束力的求解4.平动加速非惯性系的加上惯性力后牛顿定律仍然成立处理5.例题〖例2-8〗P98补例1.4〖例2-9〗P99补例1.56.习题三〖P105习题1.21，1.27，1.32，1.33〗§2-5 质点的能量(néngliàng)积分1.第一积分直接求解运动微分方程是研究动力学问题的基本方法，但对具体问题解出微分方程有时比较困难。

运动微分方程和运动方程摘要：一、运动微分方程和运动方程的定义与区别二、运动微分方程的应用领域三、运动方程的求解方法四、实际案例分析正文：运动微分方程和运动方程是物理学中关于运动规律的两种数学表达式，它们在研究物体运动过程中起着重要作用。

一、运动微分方程和运动方程的定义与区别1.运动微分方程：描述物体在某一时刻的运动状态，如速度、加速度等，是关于时间的一阶导数。

它可以表示为物体位置、速度、加速度等物理量的函数。

运动微分方程关注的是物体在某一时刻的状态，不涉及物体运动过程中的变化。

2.运动方程：描述物体在运动过程中的规律，包括动力学方程和运动学方程。

它反映了物体受到的合外力与物体运动状态之间的关系。

运动方程关注的是物体运动过程中的变化，包括速度、加速度等。

二、运动微分方程的应用领域1.经典力学：研究质点、刚体等简单物理系统的运动规律，如牛顿运动定律、拉格朗日方程等。

2.电磁学：研究带电粒子在电磁场中的运动，如麦克斯韦方程组、洛伦兹力方程等。

3.量子力学：研究微观粒子的运动，如薛定谔方程、海森堡矩阵元等。

三、运动方程的求解方法1.分离变量法：将运动方程分解为位置、速度、加速度等物理量的函数，然后分别求解。

2.特征值法：对于线性运动方程，可以通过求解特征值和特征向量来得到解。

3.数值方法：对于复杂非线性运动方程，可以采用数值方法如欧拉法、龙格-库塔法等求解。

四、实际案例分析1.抛体运动：利用运动方程研究抛体在空气阻力作用下的运动轨迹和速度变化。

2.行星运动：根据开普勒定律和牛顿运动定律，建立行星运动的运动方程，研究行星运动轨迹和速度变化。

3.电路中的粒子运动：根据电磁学方程研究带电粒子在电路中的运动，如电子、离子等。

总之，运动微分方程和运动方程在物理学领域具有广泛的应用。

双摆运动微分方程
双摆（Pendulum）运动是物理学中常见的实验装置，它能研究各种物理学现象，如重力、势能、动能转换等。

双摆运动由微积分方程来描述，这些微积分方程也被称作“双摆方程”。

双摆运动微分方程说明了双摆运动的横坐标随时间的变化，是由物理学家研究双摆运动的工具。

双摆运动的微分方程可以用数学语言描述，它可以表示为：“双摆运动的横坐
标（x）随时间（t）的变化情况，可以用微分方程dx/dt=f（x）来表示，其中f （x）表示了横坐标x随时间t的变化率。

而具体的形式可以写成x˙˙+g/l*sin （x）=0，这是双摆方程。

其中，l 代表钟摆的黎曼长度，g 代表重力加速度。

”
双摆运动的微分方程描述了双摆运动的运动规律，可以被用来研究双摆运动的
物理学行为。

双摆的位置可以用横坐标x来表示， //**横坐标的变化就是自变量，而物体**/受到的力就是因变量，由此可以用微分方程来描述。

微分方程可以用数值解法和解析解法来解决，数值解法即将积分方程近似分解，以步长求解；而解析解法则依赖于函数形式，或使用特殊函数求解，这两种方法都可以求得双摆运动的解析解。

在物理学现象中，微分方程用来描述双摆运动的运动规律是极其重要的，它的
解可以得出运动的速度、位移和势能，甚至可以分析双摆在重力场中的特殊性质。

此外，由双摆方程可以分析出双摆运动在加入外力等介质作用时，随时间变化的横坐标变化情况，因而可以更深入地探究运动的本质。

总之，双摆运动微分方程是双摆运动的定义和研究重要的工具。

它可以让我们
分析双摆数学模型的特性，也可以深入探究双摆运动的物理科学本质，进而帮助我们理解这种复杂的动态运动。

应用质点系运动微分方程的研究技术一、质点系运动微分方程的定义质点系运动微分方程是一种描述物体在特定的空间内的运动轨迹的数学方程。

它是一种描述物体运动的微分方程，可以用来求解物体在特定条件下的运动轨迹。

它是一种描述物体运动轨迹的一般微分方程，可以用来解决质点系的运动问题，它可以用来求解物体在特定条件下的运动轨迹。

质点系运动微分方程的定义是：当物体处于一定的空间中，它的运动轨迹可以用一个特殊的微分方程来描述，这个微分方程就是质点系运动微分方程。

它由一个或多个未知函数的求导与一个或多个已知函数的乘积组成，这些函数可以是时间函数、位置函数或速度函数等，只要它们满足物体运动的物理规律。

例如，用质点系运动微分方程来描述一个抛物运动的物体，可以得到一个如下的微分方程：\frac{d^2x}{dt^2}=-g，其中，g表示重力加速度。

又如，用质点系运动微分方程来描述一个摆动运动的物体，可以得到一个如下的微分方程：\frac{d^2x}{dt^2}=-\frac{g}{l}sin(x)，其中，g表示重力加速度，l表示摆的长度。

总之，质点系运动微分方程是一种描述物体在特定的空间内的运动轨迹的数学方程，它由一个或多个未知函数的求导与一个或多个已知函数的乘积组成，它可以用来求解物体在特定条件下的运动轨迹。

二、质点系运动微分方程的常见形式质点系运动微分方程是一组常见的微分方程，它们描述了质点系的运动。

它们的形式是一般的欧拉方程，也就是一阶微分方程组，其中有n个未知函数，每个函数有m个变量。

它们的具体形式是：$$\frac{d \mathbf{x}}{dt} = \mathbf{f}(\mathbf{x},t)$$其中，$\mathbf{x}$ 是质点系的状态变量，$\mathbf{f}$ 是质点系的动力学方程，描述了质点系的运动规律。

质点系运动微分方程有许多不同的形式，比如牛顿运动方程，描述了质点受到外力时的运动规律：$$m \frac{d^2 \mathbf{x}}{dt^2} = \mathbf{F}(\mathbf{x}, t)$$这里，$m$ 是质量，$\mathbf{F}$ 是外力。

3、平面运动刚体的运动微分方程平面运动刚体的运动微分方程y x C ''：过质心平移参考系平面运动随质心平移 绕质心转动()()e e ()C C C ma FJ M F α⎫=∑⎪⎬=∑⎪⎭()()2e 22e 2d d d ()d C C C r m F tJ M F t ϕ⎫=∑⎪⎪⎬⎪=∑⎪⎭投影式： ()()()e e e ()Cx xCy y C C ma F ma F J M F α⎫=∑⎪⎪=∑⎬⎪=∑⎪⎭()()()e te ne ()Ct C n C C ma F ma F J M F α⎫=∑⎪⎪=∑⎬⎪=∑⎪⎭以上各组均称为刚体平面运动微分方程平面运动刚体的运动微分方程已知：半径为r ，质量为m 的均质圆轮沿水平直线滚动，如图所示.设轮的惯性半径为，作用于轮的力偶矩为M .求轮心的加速度.如果圆轮对地面的滑动摩擦因数为f ，问力偶M 必须符合什么条件不致使圆轮滑动?C 例 1M平面运动刚体的运动微分方程解： N 2Cx Cy C ma Fma F mg m M Fr ρα⎫=⎪=-⎬⎪=-⎭()()2222N ,,,CC C C F r Mra M r m r F ma F mgρρ+==+==纯滚动的条件： s NF f F ≤即22s Cr M f mgρ+≤C a 0C a r α=分析圆轮，受力和运动情况如图所示。

由平面运动刚体运动微分方程：平面运动刚体的运动微分方程例2已知：均质圆轮半径为r 质量为m，受到轻微扰动后，在半径为R 的圆弧上往复滚动，如图所示.设表面足够粗糙，使圆轮在滚动时无滑动.求:质心C 的运动规律.平面运动刚体的运动微分方程t Ca rα=解: t sin Cma F mg θ=-C J Frα=-θcos 2mg F r R v m N C -=-()θr R s -=0d d 2322=-+s rR gt s )sin(00βω+=t s s ()r R g -=3220ω0,0v s== s 初始条件 ()gr R v s 23,000-==β运动方程为()⎪⎫ ⎛⋅-=t gr R v s 2sin 30分析圆轮，受力和运动情况如图所示。

单摆运动微分方程求解## English Response:The equation of motion for a simple pendulum is a second-order nonlinear differential equation. It is given by:$$m l \frac{d^2 \theta}{dt^2} = -m g \sin \theta$$。

where:$m$ is the mass of the pendulum.$l$ is the length of the pendulum.$g$ is the acceleration due to gravity.$\theta$ is the angle of the pendulum from the vertical.This equation can be solved using a variety of methods,including:Analytical methods: These methods involve finding an exact solution to the equation of motion. One common analytical method is to use the separation of variables method.Numerical methods: These methods involve using a computer to approximate the solution to the equation of motion. One common numerical method is to use the Runge-Kutta method.In this example, we will use the separation ofvariables method to find the analytical solution to the equation of motion. The first step is to separate the variables in the equation of motion:$$m l \frac{d^2 \theta}{dt^2} = -m g \sin \theta$$。