当前位置：文档之家 › 第06课 多自由度系统的运动方程

第06课 多自由度系统的运动方程

  • 格式：ppt
  • 大小：2.39 MB
  • 文档页数：49

下载文档原格式

  / 49

合集下载

多自由度系统振动

多自由度系统振动


= ……
φn(i )
(i ) xn
第 i 阶特征向量φ(i ) 中的一列元素，就是系统做第 i 阶主振动时 各个坐标上位移（或振幅）的相对比值
φ(i ) 描述了系统做第 i 阶主振动时具有的振动形态，称为第 i 阶
主振型，或第 i 阶模态 虽然各坐标上振幅的精确值并没有确定，但是所表现的系统振动 形态已确定 主振动仅取决于系统的 M 阵，K 阵等物理参数。
2 φ=0 或直接用 ( K − ω M )
令主振动：
⎡ x1 ⎤ ⎡φ1 ⎤ ⎢ x ⎥ = ⎢φ ⎥ sin(ωt + ϕ ) ⎢ 2⎥ ⎢ 2⎥ ⎢ ⎣ x3 ⎥ ⎦ ⎢ ⎣φ3 ⎥ ⎦
得：
2006年5月4日 《振动力学》
⎡3k − mω 2 ⎢ ⎢ −k ⎢ 0 ⎣
−k 2 k − mω 2 −1
⎤ ⎡φ1 ⎤ ⎡0⎤ ⎥⎢ ⎥ ⎢ ⎥ ⎥ ⎢φ2 ⎥ = ⎢0⎥ 3k − mω 2 ⎥ ⎣φ3 ⎥ ⎦ ⎢ ⎣0 ⎥ ⎦ ⎦⎢ 0 −k
24
多自由度系统振动 / 多自由度系统的自由振动
⎡3k − mω 2 ⎢ ⎢ −k ⎢ 0 ⎣ −k 2k − mω 2 −1 ⎤ ⎡φ1 ⎤ ⎡0⎤ ⎥ ⎥ ⎢ ⎥ − k ⎥⎢ ⎢φ2 ⎥ = ⎢0⎥ 3k − mω 2 ⎥ ⎣φ3 ⎥ ⎦ ⎢ ⎣0 ⎥ ⎦ ⎦⎢ 0
m 令α = ω2 k
⎡3 − α ⎢ −1 ⎢ ⎢ ⎣ 0
− 2 −α −1
0 ⎤ ⎡φ1 ⎤ ⎡0⎤ ⎢φ ⎥ = ⎢0⎥ −1 ⎥ ⎥⎢ 2 ⎥ ⎢ ⎥ 3 −α ⎥ ⎦⎢ ⎣φ3 ⎥ ⎦ ⎢ ⎣0 ⎥ ⎦
令特征矩阵的行列式＝0
2 ( 3 − α )( α − 5α + 4) = 0 特征方程：
6多自由度系统振动c

6多自由度系统振动c

2 1
k (2 2 ) m
2 2
k 2 m
2 3
k (2 2 ) m
2 4
在正则坐标中分两种情况求解 x （1）i 1 时 1 0 运动方程：N1 0
x 初始条件： N1 (0) 0 xN1 (0) m v
解： x N1 at b
假使 12 是 r 重根
2 即有：12 2 r2
2 r21 ,, n 都是单根 其余的
将 2 12 代入特征值问题表达式： ( K 2 M ) 0 φ 1
rank[ K 12 M ] n r 特征矩阵[ K M ] 的秩：
2 1
令： X ΦN X N
得： X N ΛX N 0
2 x 展开，得： Ni i xNi 0
X N [ xN1
xN 2
xN 3
xN 4 ]T
(i 1 ~ 4)
1 T 初始条件： X N (0) ΦN X 0 [0 0 0 0]
X N (0) ΦN1 X 0 m v[1 0 1 0]T
多自由度系统振动 / 频率方程的零根和重根情形
• 频率方程的重根情形
在前面引入振型矩阵（或模态矩阵）的概念时，曾假设所有的 特征值都是特征方程的单根 。
复杂的系统中会出现某些特征根彼此很接近甚至相等的情况 例如，柔性航天结构
下面讨论如何求出系统固有频率出现重根时的相互正交的主振 型问题
多自由度系统振动 / 频率方程的零根和重根情形
求得固有频率：
12 0 方法一：
k m k 2 2 (2 2 ) m
2 2 (2 2 )
k m k 32 2 m
第二章(多自由度系统的运动微分方程)详解

第二章(多自由度系统的运动微分方程)详解


k11 k 21 kN1
k1 j k2 j k Nj
k1N k2 N k NN
刚度影响系数 kij ：第 j 个自由度产生单位位移，其他自由度位移为零时， 需要在第i 自由度处沿着位移方向施加的力。
用影响系数法建立系统的运动微分方程
【例】用影响系数法写出图示系统的刚度矩阵。
多自由度振动系统
Piezoelectric actuator
基于压电作动器的垂尾抖振主动抑制 （此系统有一、两千个自由度（3D实体单元） ）
Z Y
X
第二章： 多自由度系统的运动 微分方程
第二章:多自由度系统的运动微分方程
第一讲：
1.建立多自由度系统运动微分方程的 各种方法的概述 2.用牛顿第二定律列写系统的运动微 分方程 3.用影响系数法建立系统的运动微分 方程
F1 1
k3
m2
k2 (d11 d21 )
m1
k2 (d11 d21 ) k1d11 1
d 21 k2 (d11 d21 )
F2 0
d11
k3d21
k2 k3 k1k2 k1k3 k2 k3 k2 k1k2 k1k3 k2 k3
m2
d 21
k2 (d11 d21 ) k3d21 0
上次课内容回顾
3.刚度影响系数
刚度影响系数 kij ：第 j 个自由度产生单位位移，其他自由度位移为零时， 需要在第 i 自由度处沿着位移方向施加的力。
4.柔度影响系数
柔度影响系数 dij ：第 j 个自由度上作用单位力，其他自由度作用力为零时，
在第 自由度上产生的位移。 i
5.刚度矩阵和柔度矩阵的关系
结构动力学多自由度

结构动力学多自由度


▪ 振型方程：
(K i2M)ji 0 (i 1, 2, 3, n)
▪∵
K 2i M 0
▪ ∴ 第i 个振型方程中的n 个方程中只有n-1个是独立的！ ▪ ——无法得到j1i、 j2i、 … 、 jni 的确定值， ▪ 但可以确定各质点振幅之间的相对比值： ▪ —— 振型的幅值是任意的，但形状是惟一的。
一致质量矩阵：
L
pava m13v1 0 fI ( x)v( x)dx
L
0
m( x) 3( x)v3
L
1( x)v1dx
mij 0 EI ( x)i ( x) j ( x)dx
L
cij 0 c( x) i ( x) j ( x)dx
其中，c(x)表示分布的粘滞阻尼特性。
一致节点荷载
L
vˆ 表示体系的形状，不随时间变化。
v 2vˆ sin(t ) 2v 2mvˆ sin(t ) kvˆ sin(t ) 0
k 2m vˆ 0
k 2m vˆ 0
即： k 2m 0
上式的N个根，表述体系可能存在的N个振型的频率。
1
2
3
N
2)
2
)
y32
(t
)
jˆ
32
s
in
(
2
t
2
)
1
jˆ
2i
yi
(t
)
jˆ3i
s
in(i
t
i
)
jˆ ni
1
jˆ 21
jˆ 31
jˆ 32
1
jˆ 22
将N个振型中的每一振型形式，用F表示N个振型所组成的方阵。
11 12 13 1N
动力学与控制-多自由度系统数值计算(1)直接积分法

动力学与控制-多自由度系统数值计算(1)直接积分法

{x(t )} 15 25 3 { X 1} cos(1t ) 66 15 25 3 { X 2 } cos( 2t ) 66 5 1 11 3
直接积分法
• 中心差分法
将ti时刻的速度、加速度向量近似地表示为
}i {x 1 ({x}i 1 {x}i 1 ), 2 t 1 }i 2 ({x}i 1 {x}i 1 2{x}i ). { x t (
12
2
2015/5/15
直接积分法
直接积分法
为了使用Runge-Kutta公式，先把振动方程改写为一 ，则 阶方程组的形式。记 y x
Cy Kx F (t ) My
• Runge-Kutta方法
求解一阶方程组
f ( z, t ) z
的(一种)四阶Runge-Kutta公式是
[ M ]{x}i 1 {F }i , i 1,2, , n 1
直接积分法
}0 [ M ]1 ({F }0 [C ]{x }0 [ K ]{x}0 ) { x
(A.5)
数值计算时，时间步长t受系统的最高频率限.3)为线性方程组，可以从中解出{x}i+1。但是, {x}1 不能由此得到。引入虚拟的{x}-1(辅助量，没有物理 意义)，根据(A.1)得到
2015/5/15
直接积分法
多自由度系统的运动方程：
} [C ]{x } [ K ]{x} {F (t )} [ M ]{ x
(1)
动力学与控制
初始条件： (2) 假定需要计算 [0,T] 时段的响应(位移、速度或者加速 度向量)。为此，我们把时间全程划分为n个等距离时 间子域，记 t T / n ，以确定时刻
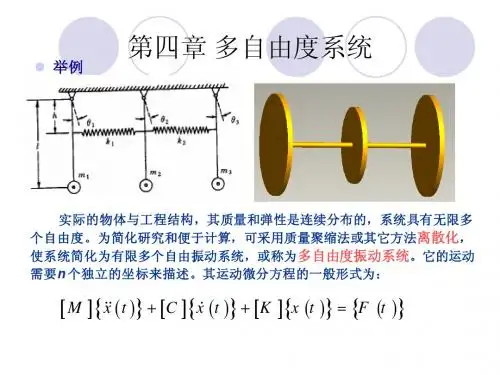
第四章 多自由度系统

第四章 多自由度系统


I1 [M ] =
I2
1 = 1960 1 kg ⋅ m 2 ) ( I3 1
第二节 无阻尼自由振动和特征值问题
− k1 0 k1 2 −2 0 由刚度影响系数法得： 由刚度影响系数法得：[ K ] = −k1 k1 + k2 −k2 = 0.98 ×107 −2 3 −1 ( N ⋅ m / rad ) 0 0 −1 1 −k2 k2 ɺɺ 1 θ1 2 −2 0 θ1 0 则作用力方程为： 则作用力方程为： 1960 1 θ 2 + 0.98 ×107 −2 3 −1 θ 2 = 0 ɺɺ θ ɺɺ 0 −1 1 θ3 0 1 3
ɺ x [ M ]{ɺɺ( t )} + [C ]{ x ( t )} + [ K ]{ x ( t )} = {F ( t )}
第一节 运动微分方程的建立
一、牛顿力学法
包括能量法、牛顿运动定律、动量定理、动量矩定理、 包括能量法、牛顿运动定律、动量定理、动量矩定理、定轴转动微分 方程、动能定理等诸多方法。 方程、动能定理等诸多方法。
方法（ 二、分析力学—— 分析力学——Lagrange方法（第三章已介绍过） —— 方法 第三章已介绍过）
三、影响系数法
1.刚度影响系数和作用力方程 刚度影响系数和作用力方程
坐标上产生单位位移（其他广义坐标位移为零），需要在第 坐标上产生单位位移（其他广义坐标位移为零），需要在第i个广义坐 ）， 标方向所加的力。实际上就是刚度矩阵的元素 刚度矩阵的元素。 标方向所加的力。实际上就是刚度矩阵的元素。
第一节 运动微分方程的建立
自由度体系的运动方程

自由度体系的运动方程


边界条件的处理
边界条件是运动方程中需要考虑的重要因素，它决定了系统 的行为和响应。
处理边界条件的方法包括直接约束法、引入虚拟约束法、罚 函数法等。根据具体问题选择适当的处理方法，以保证求解 的准确性和有效性。
04 自由度体系的稳定性分析
线性稳定性分析
线性化方程
将非线性自由度体系线性化，得到线性微分方 程。
通过建立自由度体系的运动方程，可以分析飞行器的气动性能、稳定性、控制性能等，为航空航天器设计提供重要的技术支 持。
THANKS FOR WATCHING
感谢您的观看

解析法求解需要对方程进行数学变换 ，如分离变量法、傅里叶变换等，以 简化方程并找到解。
数值法求解
数值法求解运动方程是通过对方程进 行离散化，用一系列离散点上的数值 近似代替连续的解。这种方法适用于 复杂的问题，如多自由度振动或非线 性动力学问题。
数值法求解需要选择适当的离散化方 法和迭代算法，如有限差分法、有限 元法、龙格-库塔法等，以获得满足精 度要求的解。
确定需要优化的参数，并给出其取值范围和约束 条件。
建立约束条件
根据设计要求和实际情况，建立各种约束条件， 如几何约束、性能约束等。
优化算法的选择与实现
优化算法分类
根据设计问题的特点和要求，选择合适的优化算法，如梯度下降 法、遗传算法、模拟退火算法等。
算法实现
根据选定的优化算法，编写相应的计算程序，实现优化设计的过程。
航天器姿态控制
航天器的姿态调整是通过 控制其自由度实现的，如 俯仰、偏航和滚动三个方 向的转动。
车辆动力学
车辆的运动状态可以通过 控制其轮毂电机的自由度 进行调节，实现车辆的稳 定性和操控性。
02 运动方程的建立
第十三讲—多自由度系统的运动方程

第十三讲—多自由度系统的运动方程


−
ka2θ2
+
⎛ ⎜⎝
ka 2
+
1 2
mgl
⎞⎟⎠θ3
=
0
⎡ ⎢ ⎢
1 3
ml
2
⎢ ⎢
0
⎢
0 1 ml2 3
⎢ ⎢⎣
0
0
质量矩阵
0
⎤ ⎥ ⎥
⎡⎢ka2 ⎢
+
1 2
mgl
0
⎥⎢ ⎥⎢
−ka2
1
ml
2
⎥ ⎥
⎢ ⎢
0
3 ⎥⎦ ⎢⎣
−ka2 2ka2 + 1 mgl
2 −ka2
刚度矩阵
0
⎤ ⎥
⎥
−ka2
⎥ ⎥
θ12
+
θ
2 2
+ θ32
O1
O2
O3
a
k
k
势能
θ1
θ2
θ3
U
=
1 2
k
( aθ1
−
aθ2
)2
+
1 2
k
( aθ 2
−
aθ3 )2
+
mg
l 2
(1 −
cos θ1 )
+
mg
l 2
(1 −
cosθ2
)
+
mg
l 2
(1 −
cos θ1 )
( ) 1
2
k
( aθ1
−
aθ2
)2
+
1 2
k
( aθ 2
−
aθ3
2i
j
mij
第二章(多自由度系统的运动微分方程)详解

第二章(多自由度系统的运动微分方程)详解

f 2 (t )
k3u2
c1u1
m1
c2 (u2 u1 ) c2 (u2 u1 )
m2
c3u2
受力分析时假定两质量块均沿着坐标的正方向运动.因为这样在受力分析 时容易确定所受力的大小和方向,不容易出错.
根据牛顿第二定律，得到系统的运动方程：
m1u1 k1u1 k2 (u2 u1 ) c1u1 c2 (u2 u1 ) f1 (t ) m2u2 k2 (u2 u1 ) k3u2 c2 (u2 u1 ) c3u2 f2 (t )
Mu(t ) Cu(t ) Ku(t ) f (t )
返回
用影响系数法建立系统的运动微分方程
1.总体思路
刚度影响系数 柔度影响系数 影响系数法 阻尼影响系数
K
D
C
M
质量影响系数
用影响系数法建立系统的运动微分方程
2.刚度影响系数
0
Ku f
Mu Cu Ku f
0 第j行 k1 j 0 k 2j 1 0 k Nj 0
0, u2 1
u1 0
u2 1
k12
m1
k2
k2
k22
m2
k3
k12 k2
k22 k2 k3 k1 k2 k2 刚度矩阵： K k 2 k2 k3
k11 K k21
k12 k22
用影响系数法建立系统的运动微分方程
激振力向量
Mu(t ) Cu(t ) Ku(t ) f (t )
多自由度系统运动微分方程的一般形式
建立多自由度系统运动微分方程的各种方法的概述
[工学]6-多自由度振动_OK

[工学]6-多自由度振动_OK

固有振型、固有向量、模态向量等。显然:
([K ] i2[M ]){X (i)} {0}, (i 1, 2 n)
和两自由度一样，由上式只能求出振幅的 比值，而不能确定各振幅大小。
固有频率和特征向量只决定于系统本身的 物理特性，而与外部激励和初始条件无关， 它们都是系统的固有属性。
第6章2021多/8/自20 由度系统的振动
0
k2r (k2 k3)r 2
k3r
0
k3r
k3
第6章2021多/8/自20 由度系统的振动
6.1 多自由度系统的运动微分方程式
66
对于有分支结构的m-k-c振动系统，可以用直观
目测方法直接形成振动系统的[M]、[K] 、[C]: 1. [M]为各个质量形成的对角阵; 2. [K]或[C]中的主对角线元素kii或cii为连接在质
2.247B1 0.802B2 0.555B3 1
A11 A22 A33 0
1.802A11 0.445A22 1.247 A33 0
2.247A11 0.802A22 0.555A33 0
解出各系数即可…
作业：T6-28
第6章 多自由度系统的振动
6.2无阻尼自由振动的特征值问题 26
1.振型的基准化
由于固有振型{X(i)} 只是振幅的比例关系，
各阶振型均有一个未确定的常数比例因子。 通常假设振型的某个元素为1，则其它元素 就可以表示为此元素的倍数，这种方法或过 程就是振型的基准化。
一般假设振型的第一个元素为1。
第6章 多自由度系统的振动
6.2无阻尼自由振动的特征值问题 16
2. 振型的标准化 另外一种确定振型各元素数值的方法
x3 2.247(A1 sin1t B1 cos1t) 0.802(A2 sin2t B2 cos2t) 0.555(A3 sin3t B3 cos3t)
多自由度系统的动力学方程

多自由度系统的动力学方程

得： T T M DT M C
T T K DT K C
m 0 MC 0 I C
me m 验证： M D 2 me I me C
me 1 e m 0 1 0 m e 1 me I me2 0 1 0 I C C
C C C C C
X D [ xD , D ]T
X C [ xC , C ]T
FD [ PD , M D ]T
FC [ PC , M C ]T
1 e T 1 T F ( T ) FC X D TX C F T F T D C D 0 1 将 X D TX C 代入D点的方程，并左乘 T T ： T T K TX T T F F T T M DTX C D C D C
多自由度系统振动 / 多自由度系统的自由振动
首先讨论正定系统的主振动
KX 0 正定系统： MX
主振动： X φa sin( t ) 将常数a并入 φ 中
X R
0
n
M 正定，K 正定
φ [1 2 n ]T
X φsin( t )
2
φ 0 代入振动方程： ( K M )
多自由度系统振动 / 多自由度系统的动力学方程
矩阵形式： D k1 k 2 me x k 2 a2 k1a1 xD PD m me I me2 k a k a k a 2 k a 2 M C 2 2 D D D 2 2 1 1 1 1
1/ 2
？
(K M ) φ 0
2
Kφ Mφ
2

结构动力学多自由度



pbT
~ fpa
paT ~fpb paT ~fpb T pbT ~f T pa pbT ~fpa
故 ~f 、 k 均为对称矩阵。
单元刚度矩阵
单元刚度系数表示由单位节点位移所引起的节点力。
单元刚度系数由虚位移法求得。
例如，课本P106图11-5所示简支梁中，令a端发生单位转角， 并给该处一竖向虚位移，零外力所做的功，等于内力所做的 功。
表示一个自由度发生相应单位位移而其他节点不动时在结构中所 产生的的力。
弹性特性
柔度的定义：
~ fij —在j坐标施加单位荷载而引起的i坐标的挠度。
则任意荷载组合下： vi ~fi1 p1 ~fi2 p2 ~fiN pN
用矩阵表示：
v1



vi
v N

略去阻尼矩阵和施加的荷载向量的影响： mv kv 0
假定以上多自由度体系的振动是简谐振动：
v(t) vˆ sin(t )
vˆ 表示体系的形状，不随时间变化。
v 2vˆ sin(t ) 2v 2mvˆ sin(t ) kvˆ sin(t ) 0
k 2m vˆ 0
无阻尼自由振动—振动频率分析
k 2m vˆ 0
即： k 2m 0
上式的N个根，表述体系可能存在的N个振型的频率。
1

2




3


WE va pa v1 k13
Lபைடு நூலகம்
WI v1 0 EI ( x) 1''( x) 3''( x)dx

第六讲-多自由度方程教案

前述两自由度系统动力方程)(t P X K X M =+ （3.1） 若系统有 n 个自由度，则各项皆为 n 维矩阵或列向量。

上式中⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=nn nj n n j n j m m m m m m m m m .......................................122211111M 质量矩阵、⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=nn nj n n j n j k k k k k k k k k .......................................122211111K 刚度矩阵、 位移矩阵n T n R x x x ∈=],...,,[21X 和激励矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()()()(21t P t P t P t n P 。

方程（3.1）中当质量矩阵和刚度矩阵确定后，系统动力方程可完全确定。

M 、K 的确定（1）假设外力是以准静态方式施加于系统，加速度为零0=X，有)(t K P X =。

假设作用于系统的是这样一组外力：它们使系统只在第 j 个坐标上产生单位位移，而在其他各个坐标上不产生位移，即 ：T T n j j j x x x x x ]0,...,0,1,0,...,0[],...,,,,...,[111==+-X 代入 ：⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nj j j nn nj n n j n j n k k k k k k k k k k k k t P t P t P t211222111112100100.......................................)()()()(P 所施加的这组外力数值上正是刚度矩阵 K 的第 j 列ij k 等于在第 i 个坐标上施加的力。

结论：刚度矩阵 K 中的元素ij k 是使系统仅在第 j 个坐标上产生单位位移而相应于第 i 个坐标上所需施加的力。

(结构动力学6)多自由度体系运动方程49


第六章 多自由度体系的运动方程
建立单自由度体系运动方程的方法均可以用来建立多自 由度体系的运动方程，例如：牛顿第二定律；直接平 衡法(d’ Alember)；虚位移原理；Hamilton方程；运动 的 Lagrange 方程，都可用于多自由度体系。但基于矩 阵位移法的直接平衡方程和基于变分原理的 Lagrange 方法应用更广泛一些。前者对于多自由度体系直接应 用动平衡的概念以矩阵的形式建立体系的运动方程， 概念直观，易于通过各个结构单元矩阵(刚度矩阵、质 量矩阵、阻尼矩阵)建立整个结构体系的相应矩阵，进 而建立体系的运动方程，便于计算机编程，在结构动 力分析的有限元程序中基本上都基于直接平衡法。而 对于一些特殊的问题，例如，大变形（位移）问题， 采用 Lagrange 方法可能更有效。本章将主要介绍这两 种方法。
6.1 直接平衡法
首先复习一下结构力学中的刚度阵法（矩阵位移法） 如果为N层结构，自由度为N，每一楼层有集中质量mi， 外荷载pi，层间刚度ki，各层的水平运动为ui，i=1, …, N。这个层间模型也可以转化成质点—弹簧模型。
6.1 直接平衡法
应用d’Alember原理
f I i f D i f s i pi (t ), i 1, 2, N
fIi—惯性力； fDi—阻尼力； fsi—弹性恢复力； pi—外力。
f I
f I1 f I2 f IN

p1 (t ) p (t ) 2 p(t ) p N (t )
其中{fI}称为惯性力向量，{M}称为质量矩阵，{ü }为加速 度向量。质量矩阵中的系数mij为质量影响系数，简称质 量系数或质量，它的含义是： mij—由j自由度的单位加速度引起的相应于i自由度的力 即给定j自由度一个单位加速度，产生了惯性力，其余自 由度加速度为零时，所需要的力。

第二章多自由度系统的运动微分方程


mu(t ) cu(t ) ku(t ) f (t )
多自由度系统运动微分方程的一般形式
u(t )
u(t )
位移向量
m
阻尼矩阵
M
质量矩阵
c
f (t )
C
k
K
刚度矩阵
f (t )
激振力向量
Mu(t ) Cu(t ) Ku(t ) f (t )
多自由度系统运动微分方程的一般形式
建立多自由度系统运动微分方程的各种方法的概述
k11 k 21 kN1
k1 j k2 j k Nj
k1N k2 N k NN
刚度影响系数 kij ：第 j 个自由度产生单位位移，其他自由度位移为零时， 需要在第i 自由度处沿着位移方向施加的力。
用影响系数法建立系统的运动微分方程
【例】用影响系数法写出图示系统的刚度矩阵。
2.系统运动微分方程的建立方法
牛顿第二定律: 适用于自由度不多的离散系统或简单的 连续系统
动量矩定理:
影响系数法： 建立方法
主要适用于自由度不多的离散系统
主要适用于自由度不多的离散系统
Lagrange方程法：主要适用于离散系统
Hamilton原理：
有限单元法：
主要适用于连续系统
离散系统，连续系统都适用，是一种最
第二章:多自由度系统的运动微分方程
第一讲：
1.建立多自由度系统运动微分方程的 各种方法的概述 2.用牛顿第二定律列写系统的运动微 分方程 3.用影响系数法建立系统的运动微分 方程
建立多自由度系统运动微分方程的各种方法的概述
1.多自由度系统运动微分方程的一般形式
回想单自由度系统运动微分方程的一般形式

多自由度系统振动微分方程-6


k1n 0 k1 j k2n k2 j 1 kin kij k nn 0 k n j
应用Lagrange方程。车体振动方程为
mD m eD (k1 k2 ) xD (k2 a2 k1a1 ) D FD x
2 (k a k a ) x (k a 2 k a 2 ) M m eD ( I C m e ) D x 2 2 1 1 D 1 1 2 2 D
如此施加的外力数值上 是质量矩阵M的第j列
元素 mij 是在第 i 个 广义坐标上施加的力
质量矩阵 M 中的元素 mij 是使系统仅在第 j 个广义坐 标上产生单位加速度而在第 i 个广义坐标上所需施加的力
mij、kij分别称为质量影响系数和刚度影响系数
根据影响系数的物理意义可直接得到系统的质量 矩阵M和刚度矩阵K，这种建立振动微分方程方 法称为影响系数法
xC xD eC C D


V
1 1 2 2 k1 xD a1 D k 2 xD a2 D 2 2
确定对应广义坐标的广义力。设虚位移δxD、δθD，非有势力FD和 MD所做的虚功分别为
W1 FD xD ， W2 M D D
Q1 PD ， Q2 M D
T Qj q j
Lagrange方程的基本形式为
d T dt q j
( j 1, 2, , N )
广义力Qj的表达式为
Qj

n i 1
Fi
ri qj
主动力为有势力
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
以 m2 为研究对象，有
m2x1 k2 x1 x2 c2x1 x2 k3x2 c3x2 F2 (t)
将方程(1)、（2）整理可得
（1） （2）
m1x1 c1 c2 x1 c2x2 k1 k2 x1 k2x2 F1(t)
n
1
kn2

k1n

k2n


k
n
n

刚度影响系数 作用力方程
现分析求出图所示的三自由度系统的刚度矩阵。
首先令 x1 1 x2 x3 0 在此条件下系统保持平衡，按定义需加于三物块的力 k11、k21、k31
画出各物块的受力图根据平衡条件，有
k11 k1 k2，k21 k2，k31 0
机械振动(Mechanical Vibration)
第七课 多自由度系统的运动方程
交通与车辆工程学院 刚宪约
2019年9月15日
单自由度系统回顾
单自由度系统运动方程的建模
• 牛顿第二定律（向量方法），达朗伯原理 • 能量方法d(U+T)=0 • 虚位移原理（虚功原理）
单自由度系统固有频率计算方法
T
对于图所示的系统，也可用柔度影响系数来建立其运动微分方程。
应用叠加原理可得到 x1 (F1)11 (F2 )12 (F3 )13 x2 (F1) 21 (F2 ) 22 (F3 ) 23 x3 (F1) 31 (F2 ) 32 (F3 ) 33
0
k2 k1 k3
k3
0

k
3

k3
kij k ji
刚度矩阵一般是对称的。 实际上任何多自由度线性系统都具有这个性质。即
K KT
柔度影响系数 位移方程
在单自由度的弹簧—质量系统中，若弹簧常数是 k ，
则1 k 就是物块上作用单位力时弹簧的变形，称柔度影响
系数，用 表示。
3.1 多自由度系统的运动方程
牛顿第二定律矢量建模方法 影响系数法
• 刚度影响系数法 • 柔度影响系数法
Lagrange方程方法
• 约束、自由度与广义坐标 • Lagrange方程建模方法
约束、自由度与广义坐标
约束是对自由而言得,是一个纯运动学概念,他强调力学体系在运 动时必须满足某些规定的条件.约束条件必须通过约束方程的形式才 能确切的表示出来.

1 2
m
2
x
2 2

1 2
x1
Байду номын сангаас
,
x 2
m01
0 m2
x1


x 2


1 2
x Mx
U

1 2
k1 x12

1 2
k2 x2

x1 2

1 2
k
3
x
3 2

1 2
x1
,
x
2
k1k
k
2
2
k2 k2 k3


x1 x2
方程中各项均为力的量纲，因此，称之为作用力方程。若用矩阵表示， 则可写成
Mx Kx 0
x x1 x2 xn T，x x1 x2 xn T
式中分别是系统的坐标矢量和加速度矢量。
影响系数法
刚度矩阵中的元素称刚度影响系数(在单自由度 系统中，简称弹性常数)。它表示系统单位变形所需 的作用力。具体地说，如果使第 j 个质量沿其坐标方 向产生单位位移，沿其它质量的坐标方向施加作用力 而使它们保持不动，则沿第 i 个质量坐标方向施加的
• 根据运动方程 n2 k / m
• 能量方法Umax=Tmax • 单位加速度法
初始条件下系统的运动方程
单自由度系统回顾
等效质量与等效刚度计算
• 等效质量－－动能等效 • 等效刚度－－势能等效
阻尼自由振动
• 三种阻尼类型（粘性，库伦，结构） • 阻尼比与临界阻尼，振动方程的解，初始条件下的响应 • 对数衰减率测定系统阻尼 • 粘性阻尼与库伦阻尼的衰减特征
3.1 多自由度系统的运动方程
牛顿第二定律矢量建模方法 影响系数法
• 刚度影响系数法 • 柔度影响系数法
Lagrange方程方法 • 约束、自由度与广义坐标 • Lagrange方程建模方法
影响系数法
一般情况下，n 个自由度无阻尼系统的自由振动的运动微分方程具 有以下形式
m11x1 m12 x2 m1n xn k11x1 k12 x2 k1n xn 0 m21x1 m22 x2 m2n xn k21x1 k22 x2 k2n xn 0 mn1x1 mn2x2 mnn xn kn1x1 kn2 x2 knn xn 0
n 自由度系统的柔度矩阵 Δ 为 n 阶方阵，其元素ij 称
为柔度影响系数，表示单位力产生的位移。具体地说，仅 在第 j 个质量的坐标方向上受到单位力作用时相应于在第 i
个质量的坐标方向上产生的位移，即定义为ij 。
现分析求出图所示的三自由度系统的柔度影响系数。
FF1 1
首先施加单位力 F1 1，F2 F3 0
cij

2D xix j
kij

2U xix j
根据上式得到列系统的运动微分方程的一种 简单的方法：
• 先求出系统的动能、势能和能量耗散函数，然后 利用上式求出系统的质量矩阵、阻尼矩阵和刚度 矩阵，最终求出系统的运动微分方程。
这样的优点是，由于系统的动能、势能和能 量耗散函数是标量，可以不考虑力的方向。
31
12 22 32

13 23 33



k1 1
k1 1
k1
1
k1 11 k1 k2 11 k1 k2
1
k1

1
1 k1
1
1 k2
1

k1 k2 k3
系统的柔度矩阵为
1
11 21
这时三物块所产生的静位移分别是 11、 21、 31
1
当受到F1作用后，第一个弹簧的变形为 弹簧的变形为零。
k1
，第二和第三个
所以三物块的位移都是
11

1 k1
, 21

1 k1
, 31

1 k1
F2
令 F2 1，F1 F3 0 第一和第二弹簧均受单位拉力，其变形分别为 1 , 1
• 傅立叶级数，正弦、余弦激励函数的响应，线性叠加原理 • 脉冲函数与脉冲响应 • 卷积积分 • 频响函数、脉冲响应函数与传递函数之间的关系
本章主要内容
3.1 多自由度系统的运动方程 3.2 频率方程、振型与正则坐标 3.3 多自由度系统的振动响应 3.4 多自由度系统的数值计算方法
k1 k2 第三个弹簧不受力，故其变形为零。因此有
12

1 k1
, 22

1 k1

1 k2
, 32

1 k1

1 k2
F3
再令 F1 F2 0, F3 1
可得到
13

1 k1
, 23

1 k1

1 k2
, 33

1 k1

1 k2

1 k3
系统的柔度矩阵为
1
11 21
同理，令 x1 0，x2 1，x3 0
画出受力图，则有 k12 k2 ，k22 k2 k3，k32 k3 最后令 x1 x2 0，x3 1
画出受力图，有 k13 0，k23 k3，k33 k3
因此刚度矩阵为
k1 k2
K


k2
3.1 多自由度系统的运动方程
牛顿第二定律矢量建模方法 影响系数法
• 刚度影响系数法 • 柔度影响系数法
Lagrange方程方法
• 约束、自由度与广义坐标 • Lagrange方程建模方法
牛顿第二定律建模
以 m1 为研究对象，有
m1x1 k1x1 k2x2 x1 c1x1 c2 x2 x1 F1(t)
单自由度系统回顾
简谐强迫振动
• 简谐强迫振动的解，复指数法 • 频响函数与频响特性曲线 • 品质因数与半功率带，半功率带法测量阻尼 • 旋转失衡与基础振动引起的简谐强迫振动方程、频响函数 • 积极隔振与消极隔振原理 • 位移传感器与加速度传感器的频响特性
单自由度系统回顾
周期强迫振动与非周期强迫振动
系统运动时，质量的惯性力使弹簧产生变形 x1 (m1x1 ) 11 (m2 x2 ) 12 (m3 x3 ) 13 x2 (m1x1 ) 21 (m2 x2 ) 22 (m3 x3 ) 23 x3 (m1x1 ) 31 (m2 x2 ) 32 (m3 x3 ) 33

x1 x2


k1 k2

k2
k2 k2 k3


x1 x2



F1 F2
(t) (t)
即
Mx Cx kx F(t)
Mx Cx kx F(t)
这种用矩阵写出的运动微分方程与单自由度系统的 运动微分方程非常相似。
（3）
m2x1 c2x1 c2 c3 x2 k2x1 k2 k3 x2 F2 (t) （4）