力偶

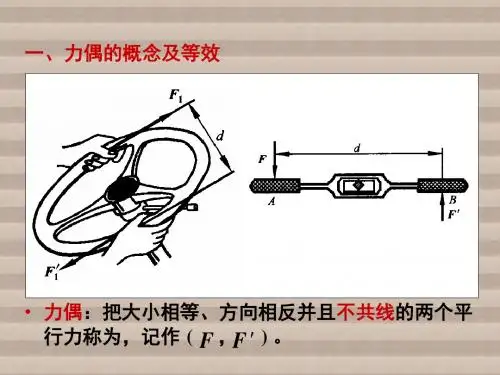
力偶产生的弯矩
力偶是指作用在物体上的两个相等大小、方向相反的力，它们的作用线通过物体的转轴。

力偶产生的弯矩可以通过以下公式计算：
M=F×d
其中，M表示力偶产生的弯矩，F表示每个力的大小，d 表示力之间的距离。

注意，这里的距离$d$是指垂直于力的作用线的最短距离。

需要注意的是，如果力偶所形成的平面与物体的转轴垂直，那么力偶产生的弯矩将是最大的。

当力偶形成的平面与转轴呈角度时，弯矩的大小将随着夹角的变化而减小。

总结起来，力偶产生的弯矩大小与力的大小和力之间的距离有关。

力偶知识点总结一、力矩的定义力矩（Torque）又称力偶，是一个由力和力臂构成的物理量。

在力矩的定义中，力臂是指力的作用线与旋转轴之间的垂直距离，而力矩的大小可以用力矩的模进行描述，方向则由右手法则确定。

一般来说，力矩可以分为正向力矩和负向力矩，具体取决于力的方向和作用点位置。

正向力矩能够使物体绕旋转轴顺时针旋转，而负向力矩则会使物体逆时针旋转。

二、力矩的计算力矩的计算公式为：M=rFsinθ，其中M是力矩的大小，r是力臂的长度，F是作用力的大小，θ是力相对于力臂的夹角。

需要注意的是，力矩的大小与力的大小、力臂的长度以及力的夹角都有关系，当这些因素改变时，力矩的大小也会相应地改变。

为了更好地计算力矩，我们还可以利用向量叉积的方法，通过叉积的运算得到力矩的大小和方向。

具体地，如果我们知道力矩的作用点、力的作用点以及力的方向，就可以利用向量叉积得到力矩的大小和方向。

力矩的计算方法有很多种，但无论采用何种方法，都需要注意力的方向以及作用点的位置，以保证计算结果的准确性。

三、力矩与力的关系力矩与力之间存在着密切的关系，力是产生力矩的基础，力矩则是力在旋转过程中所产生的影响。

如果一个物体受到一个力，而力的作用线与旋转轴不重合，就会产生力矩。

同时，力矩也可以通过力的大小、方向以及作用点的位置来计算。

根据力矩的定义以及力和力矩之间的关系，我们可以得出结论：力矩与力之间存在着正向关系，即力的大小增大，则力矩的大小也会增大；力矩与力臂之间也存在着正向关系，力臂越长，则力矩的大小也会越大。

力矩的大小还与力的方向以及作用点的位置有关系，只有在旋转轴上的力矩才为零，其他情况下，力矩都会产生。

四、力矩平衡条件在物体平衡的情况下，力矩也处于平衡状态。

力矩的平衡条件可以由力矩平衡方程来描述。

在平衡状态下，物体所受的合外力矩和合内力矩都为零，这就是力矩平衡条件。

具体地，力矩平衡条件可以用以下公式来表示：ΣM=0，即所有作用在物体上的力矩的和都为零。

力矩力偶的概念一、概念介绍力矩和力偶是力学中的重要概念，用于描述物体受到的转动效应。

力矩是由一个力在物体上产生的旋转效果，而力偶则是由两个相等大小、方向相反的力所产生的旋转效果。

二、力矩的定义与计算1. 定义：力矩是指一个作用在物体上的力对该物体产生旋转效应的量度。

2. 计算：力矩等于作用在物体上的力与该力距离物体某一点（通常为旋转中心）的垂直距离之积。

即M = Fd，其中M为力矩，F为作用在物体上的力，d为该力距离旋转中心的垂直距离。

三、影响因素1. 力大小：当施加于物体上的外部作用力增大时，其所产生的旋转效应也会增大。

2. 作用点位置：当外部作用点远离旋转中心时，其所产生的旋转效应也会增大。

3. 旋转中心位置：当旋转中心移动到距外部作用点更远处时，其所产生的旋转效应也会增大。

1. 机械工程：力矩被广泛应用于机械工程中，例如在汽车发动机的设计中，需要计算发动机输出的扭矩大小，以及通过传动系统将扭矩传递到车轮上。

2. 物理学：力矩被用于解释天体运动和物体旋转的现象，例如地球公转和自转、陀螺运动等。

3. 运动学分析：力矩可以用于分析人体运动时的肌肉力量作用，例如在举重运动中，需要计算出各个关节处所受到的力矩大小。

五、力偶的定义与计算1. 定义：力偶是由两个相等大小、方向相反的力所产生的旋转效应。

2. 计算：力偶等于两个相等大小、方向相反的力之间距离（称为臂长）之积。

即C = Fd，其中C为力偶大小，F为每个作用在物体上的相等大小、方向相反的力，d为两个作用点之间距离。

六、影响因素1. 力大小：当施加于物体上的外部作用力增大时，其所产生的旋转效应也会增大。

2. 作用点位置：当外部作用点远离旋转中心时，其所产生的旋转效应也会增大。

3. 两个作用点之间的距离：当两个作用点之间的距离增大时，其所产生的旋转效应也会增大。

1. 物理学：力偶被广泛应用于解释天体运动和物体旋转的现象，例如在行星公转和自转、陀螺运动等。

1、力矩是一个向量，可以被想象为一个旋转力或角力，导致出旋转运动的改变的力力偶是作用于同一刚体上的一对大小相等、方向相反、但不共线的一对平行力，可以理解为力矩的代数和。

2、力偶中两个力之间的垂直距离d 称为力偶臂。

3、力偶中的力F与力偶臂d 的乘积称为力偶矩。

4、他两的区别是力偶就只有两个方向,力距可以多个力多个方向。

5、力偶矩与力矩的区别是力矩的大小、正负与力和矩心的相对位置有关；力偶对任一点之矩均等于力偶矩。

力偶矩可以完全描述一个力偶；力对点之矩不能完全描述一个力偶。

6、力矩在物理学里是指作用力使物体绕着转动轴或支点转动的趋向。

力矩的单位是牛顿-米。

力矩希腊字母是tau。

力矩的概念，起源于阿基米德对杠杆的研究。

转动力矩又称为转矩或扭矩。

力矩能够使物体改变其旋转运动。

推挤或拖拉涉及到作用力，而扭转则涉及到力矩。

力矩等于径向矢量与作用力的叉积。

力矩和力偶
力矩和力偶是力学中的两个基本概念，它们在力的作用方式和使用效果上存在一些区别。

力矩是一个向量，它描述了力对物体产生转动作用的效果，是力对某一轴线或点的作用力矩。

力矩的大小等于力的大小和其到旋转轴或点的距离的乘积，方向垂直于轴或点。

在计算上，力矩等于力与力臂的乘积，其中力臂是从旋转轴或点到力的作用线的垂直距离。

力偶是一对大小相等、方向相反且不共线的平行力，它们的作用效果是使物体产生转动。

这对力在相互垂直的平面上，其中一个力垂直于这个平面，另一个力平行于这个平面。

在实际应用中，力偶可以用来转动锁紧物体，例如螺栓、螺母等。

综上所述，力矩和力偶虽然都涉及到力的作用，但它们的作用方式和使用效果有所不同。

力矩描述的是力对物体产生转动作用的效果，而力偶则是一种产生转动作用的特殊方式。

工程力学中的力矩和力偶力矩和力偶是工程力学中重要的概念，在力学计算和结构设计中发挥着重要的作用。

本文将详细介绍力矩和力偶的定义、计算方法以及应用。

一、力矩的定义和计算方法力矩是描述力的作用于物体时产生的转动效应的物理量。

力矩可以通过施加力与物体距离的乘积来计算，其计算公式为：力矩 = 力 ×距离其中，力矩的单位是牛顿·米（N·m），力的单位是牛顿（N），距离的单位是米（m）。

力矩的计算过程需要确定力的大小、方向以及力作用点到转轴的距离。

如果力作用点与转轴垂直且在同一平面上，那么力矩可以简化为：力矩 = 力 ×距离× sin(θ)其中，θ为力的作用方向与力臂方向之间的夹角。

二、力偶的定义和计算方法力偶是指两个大小相等、方向相反的力在同一直线上同时作用于物体上，力矩大小相等但方向相反。

力偶可以看作是一对平行力的叠加。

力偶的计算方法为力乘以力臂的差值，即：力偶 = 力 ×力臂差值其中，力偶的单位也是牛顿·米（N·m），力的单位是牛顿（N），力臂的单位是米（m）。

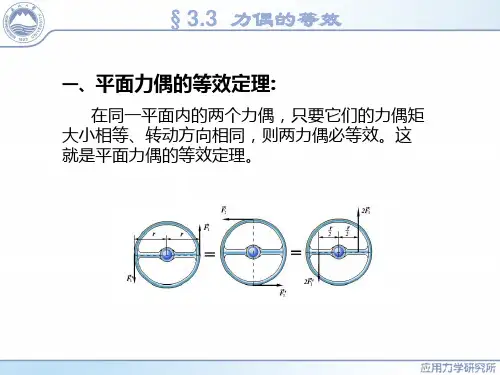
三、力矩和力偶的应用1. 平衡条件分析：力矩和力偶在平衡条件的分析中起到重要作用。

根据力矩的定义，物体处于平衡状态时，所有作用在物体上的力矩的合力为零。

通过计算各力矩的代数和，可以判断物体是否处于平衡状态。

2. 结构设计：在建筑和桥梁等结构设计中，力矩和力偶的分析是不可或缺的。

通过分析结构受力情况，可以确定合理的支撑结构和材料选择。

3. 机械传动系统：力矩和力偶在机械传动系统中也有广泛应用。

例如，齿轮传动中的扭矩计算和风力发电机组的叶片受力分析等都需要使用力矩和力偶的概念。

4. 车辆动力学：在车辆动力学中，力矩和力偶的应用十分广泛。

例如，车辆启动时的转矩计算、制动时的负载分析以及悬挂系统的设计等都需要借助力矩和力偶的概念进行分析。

总结：力矩和力偶是工程力学中的重要概念，具有广泛的应用。

力偶的术语解释力偶是物理学中的一个重要概念，它用来描述两个相等大小、方向相反的力在同一直线上作用的情况。

力偶常用于解释物体的旋转运动以及平衡条件。

本文将对力偶的定义、力矩和力偶对物体的影响等方面进行解释。

1. 力偶的定义力偶是指两个大小相等、方向相反的力在同一直线上作用的情况。

记作F1与F2为力偶两个力的大小，d为力偶的臂长（即两个力之间的距离），力偶可以表示为M = F1 × d = F2 × d。

其中M表示力偶的力矩。

力偶既是力的叠加，又是力矩的叠加。

2. 力矩力矩是力对物体产生旋转效应的物理量，用M表示，其计算公式为M = F × d。

其中F表示力的大小，d表示力的作用点到物体指定轴线的距离，力矩的单位是牛顿·米（N·m）。

3. 力偶对物体的影响力偶的作用方式是使物体发生转动。

当一个力偶作用在物体上时，力偶的力矩将使物体绕一个轴线旋转。

根据力矩的性质，力偶对物体的效果与其力矩有关。

当物体所受力矩为零时，物体处于平衡状态。

4. 力偶的平衡条件力偶的平衡条件是指力偶对物体的合成力矩为零。

当一个物体对称地受到力偶的作用时，力偶的合成力矩为零，物体将保持平衡。

利用力偶的平衡条件可以解释物体的静力平衡与旋转平衡。

5. 力偶与杠杆原理力偶与杠杆原理密切相关。

根据杠杆原理，一个物体平衡时，物体所受力偶的力矩之和为零。

利用杠杆原理可以计算物体上未知力的大小或位置。

6. 力偶的应用力偶的概念在物理学和工程学中有着广泛的应用。

在机械工程中，力偶可以用于分析物体的平衡问题和旋转运动；在土木工程中，力偶可以用于计算桥梁和结构的稳定性；在天文学中，力偶可以用于解释天体的自转现象。

总结：力偶是两个大小相等、方向相反的力在同一直线上作用的情况。

力偶的定义、力矩与力偶的关系、力偶对物体的影响和平衡条件等方面进行了解释。

力偶的概念在物理学和工程学中有着广泛的应用，对于理解物体的平衡和旋转运动以及解释天体自转等现象具有重要意义。

§1-3 力偶一力偶的概念1．力偶：大小相等，方向相反，作用线平行但不重合的二力组成的力系，称为力偶。

记作（F，F、）。

2．力偶矩：力偶（F，F、）的力偶矩，以符号M（F，F、）表示，或简写为M。

∴M=±FLd(1)方向：逆时针方向为正，顺时针方向为负。

(2)力偶的转动效应：力偶矩的大小；力偶的转向；力偶作用面的方位。

二力偶的基本性质1．力偶中两个力在力偶的作用平面内任一坐标轴上的投影的代数和等于零，因而力偶无合力。

力偶本身不平衡。

2．力偶不能用一个力来代替，也不能用一个力来平衡，力偶只能用力偶来平衡。

注意：(1)力和力偶是力学中两个基本量，不能互相代替。

(2)力矩和力偶相同点：都能使物体转动状态发生改变。

(3)不同点：力矩使物体转动效应与矩心的位置有关；力偶对其作用平面内任一点的矩为常数，且等于本身力偶矩。

三推论：等效力偶：力偶矩大小相等且转向相同，这两个力偶对物体有相同的转动效应，我们称为等效力偶。

1.力偶可以在它的作用面内任意移动和转动，而不改变它对物体的作用效果。

2.同时改变力偶中力的大小和力偶臂的长短，只要保持力偶矩的大小和力偶的转向不变，就不会改变力偶对物体的作用效果。

§1-4 力的平移定理一证明：如图所示：设刚体上有一力F作用，现在我们把作用在刚体上A点的力F平行移动到刚体上任一点O的等效条件进行推导：(1)在刚体上任意取一点O 。

(2)在O点上加一对等值，反向的力F1和F2。

(3)保证F1和F2与力F平行且大小相等，即F1=F2=F。

(4)由图可知，由F，F1，F2组成的新力系和原来的一个力F等效，可看作是一个作用于O点的力和一个力偶（F1，F2）。

小结：由以上分析可以知道，把作用在A点的力F平移到刚体的O点时，若使其作用在A 点等效，必须同时要加一个相应的力偶，这个力偶称为附加力偶。

附加力偶的矩用下式表示：M=Mo(F)=-FLd二力的平移定理：若将作用在刚体上某点的力平移到刚体上另一点，而不改变原力的作用效果，则必须附加一个力偶，其力偶矩等于原力对新作用点的矩。

组成力偶的两个力的特点组成力偶的两个力的特点在物理学中，力偶是指两个大小相等、方向相反、作用线共线的力所形成的力对。

组成力偶的两个力具有相互作用、大小相等、方向相反、作用线共线的特点。

本文将分别从这四个方面进行详细阐述。

首先，组成力偶的两个力具有相互作用的特点。

在形成力偶的过程中，两个力是相互作用的。

一个力偶由两个力组成，当一个力施加在一个物体上时，另一个力必然施加在另一个物体上。

这种相互作用的特点体现了力偶的力对性质，使得力偶对物体的作用不会单方面。

其次，组成力偶的两个力大小相等。

力偶的定义要求两个力的大小相等，这是形成力偶的基本条件之一。

而且，两个力的大小相等使得力偶不会产生单一的力效果，从而避免了对物体的单一推拉作用，使得物体更加稳定。

第三，组成力偶的两个力方向相反。

力偶的两个力在作用线上相对而行。

这种反方向的特点使得力偶的单一效果相互抵消，对物体的作用更平衡。

同时，方向相反的两个力使得力偶的合力为零，不会对物体产生整体的加速度，保持物体的静止或动态平衡。

最后，组成力偶的两个力作用线共线。

作用线共线的特点体现了力偶的力偶臂，即力的作用线与力偶的作用线之间的垂直距离。

共线的作用线使得力矩的计算更加简单。

力偶臂的长度越大，力偶在物体上产生的力矩越大，物体受到的作用力也就越大。

力偶臂的方向决定了力矩的方向，力偶对物体的转动效果就取决于这个方向。

综上所述，组成力偶的两个力具有相互作用、大小相等、方向相反、作用线共线等特点。

这些特点共同构成了力偶的基本属性，使得力偶成为一种重要的力对形式。

力偶在物体的平衡、转动、静力学等领域中有着广泛的应用。

深入理解和掌握力偶的特点，对于解决力学问题、提高分析能力具有重要意义。

力偶和弯矩
弯矩：受力构件截面上的内力的一种,其大小为该截面截取的构件部分上所有外力对该截面形心矩的代数和。

力偶：大小相等、方向相反、作用线不在同一直线上的一对力.对物体产生转动效应,作用面具有方向性。

力矩，力偶矩，弯矩有区别；
一、性质不同
1、力矩是线型力叉乘径长。

2、力偶是大小相等，方向相反，不在同一直线上的一对平行力。

3、力偶矩是力矩与力偶的乘积。

二、使用单位不同
1、力矩使用的是长度单位（米、分米、厘米等）。

2、力偶使用的是力学单位——牛顿。

3、力偶矩使用单位是复合单位——牛×米。