平面力偶系
- 格式:ppt
- 大小:864.00 KB
- 文档页数:25


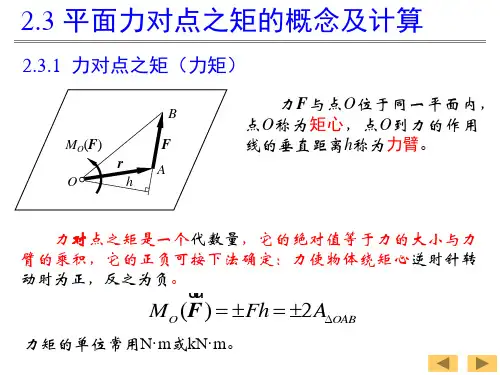




平面力偶系的合成与平衡条件引言平面力偶系是力学中一个重要的概念,它由两个等大、相对且反向的力组成。
在物体的力学分析中,我们经常需要考虑多个力对物体的合成效果以及力矩对物体的平衡条件。
本文将详细探讨平面力偶系的合成原理与平衡条件,并通过数学推导和实例分析来加深对这一主题的理解。
平面力偶系的合成平面力偶系的特点平面力偶系由两个大小相等、方向相反、作用线相交的力构成。
这两个力又被称为偶力对。
平面力偶的合成原理平面力偶系的合成原理是根据力的合成规律:力的合成等于力的矢量和。
对于平面力偶系,我们可以将两个偶力看作同时作用在物体上的两个力,然后将它们的合力作为合成后力的大小和方向。
平面力偶的合成公式设两个偶力分别为F1和F2,作用在物体上的力矩分别为M1和M2。
则它们的合力F和合力矩M满足以下关系式: - F = F1 + F2 - M = M1 + M2平衡条件的推导平衡条件的定义当物体所受合力为零,并且合力矩也为零时,物体处于力学平衡状态。
在平面力偶系中,平衡条件可以通过分析合力和合力矩的关系来推导。
平衡条件的数学推导设物体所受力偶为F,力矩为M。
根据平面力偶的合成公式可知,F = F1 + F2。
因为合力为零,所以F1 = -F2。
根据力矩的定义,力矩M = rF,其中r为力矩臂,即力的作用线到转轴的垂直距离。
考虑到F1和F2的作用线分别经过转轴的上侧和下侧,它们的力矩方向相反,即M1 = -M2。
于是,合力矩M = M1 + M2 = -M1 + M2 = 0。
平衡条件的几何推导另一种推导平衡条件的方法是通过几何关系。
对于一个平面力偶系,其合力矩为零意味着力偶矢量的作用线经过转轴。
这是因为力偶矢量的大小和方向固定,只要作用线改变,合力矩就不会为零。
因此,合力矩为零是平衡条件的几何解释。
平面力偶系的平衡例子为了更好地理解平面力偶系的合成和平衡条件,我们来看一个简单的例子。
假设有一个悬挂在弹簧上的质点,上方有一个对称的平面力偶系作用在它上面。


平面汇交力系和平面力偶系
平面汇交力系和平面力偶系是平面力学中的两个重要概念。
平面汇交力系是指各力的作用线在同一平面内且汇交于一点的力系。
在平面汇交力系中,力的大小和方向可以通过力的矢量表示。
平面汇交力系的合成可以通过力的多边形法则来进行,即将各个力按照首尾相接的顺序连接起来,形成一个封闭的多边形,合力则为这个多边形的封闭矢量。
平面力偶系是指由若干个力偶组成的力系,其中力偶是由大小相等、方向相反且不共线的两个力组成的力矩对。
在平面力偶系中,力偶的作用效果是产生旋转,而不是平移。
平面力偶系的合成可以通过力偶矩的代数和来进行。
平面汇交力系和平面力偶系在工程和物理学中有广泛的应用。
在结构分析、机械设计和力学问题中,常常需要考虑和分析平面汇交力系和平面力偶系的作用效果。
总的来说,平面汇交力系和平面力偶系是平面力学中的重要概念,它们的合成和平衡条件对于理解和解决平面力学问题至关重要。

平面力偶系
注平面力偶系是一种新兴概念,旨在改善视觉对抗环境,通过利用环境协调力。
平面力偶系是指在居家空间中创建出一种力学和美学协调性,配合一起使用,以强调自身空间中物体表面上力学和美学各自的特性,使空间自身变得更实用更美观。
这种方式可以帮助空间更加有序的形成从外观上能够展现出一种熟悉的力学效果,更加有趣、新颖。
拥有平面力偶系的装饰方式很多,可以从家居细节的创意中查看,比如以一种大格局的视角,产生一种混合空间的活动性;体现空间整体形态的轮廓中,也可以追求一种显而易见的视觉力图状态;更可以加入颜色偏好,营造出一种低调静谧的安静情调;当然,在装饰设计的本质上,追求平面力偶系的空间主题也能给我们带来许多独特的情感体验。
其实,平面力偶系是一种理念性的整合装饰方案,它利用环境现存的元素和元素相互作用产生的变化,使空间形成一种易懂、通俗易懂的平衡状态,以便实现平稳、融和的内部空间感受。
平面力偶系也包括多种设计手法,如审美观、光线处理、色彩搭配等,如果有意地结合,可以产生一种新颖的空间体验,营造出一种舒适、自然而又精心设计的家的空间感受,为家本身营造出一种浑然天成的氛围。
通过采用这种装饰方式,不仅可以改善室内质感,为人们也营造出一种高品质的生活体验,让大家能够体会到环境中不可思议的美好。