力偶理论
- 格式:ppt
- 大小:327.00 KB
- 文档页数:17









自然科学史与方法论力偶
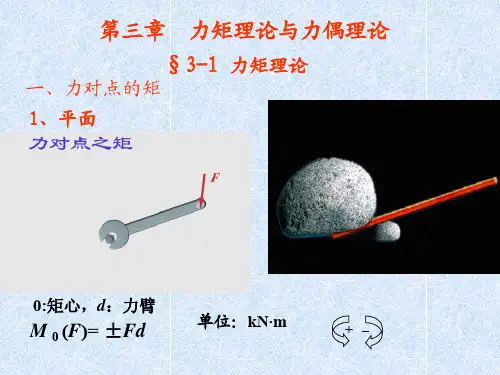
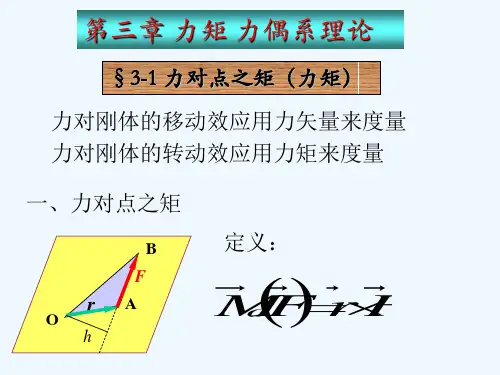
力偶是指两个力的大小相等、方向相反的力的作用,它们的作用
线在同一直线上。
力偶在物理学中有着广泛的应用,特别是在机械领域。
在自然科学史中,力偶的概念可以追溯到古希腊时期。
阿基米德
就研究过力偶的性质,他提出了“浮力原理”,即浮在液体中的物体
会受到一个向上的浮力,其大小等于被物体排开的液体重量。
阿基米
德用力偶的概念来解释这一现象,证明了浮力取决于物体与液体的体
积关系。
在物理学的发展过程中,力偶的应用也有了一系列的拓展。
牛顿
力学中的“作用与反作用定律”实际上就是力偶的体现。
在静力学中,力偶可以用来计算物体的转动。
在航空航天领域中,力偶也是非常重
要的概念,例如,在飞机的气动设计中,力偶可以用来平衡机翼上的
扰流器对飞机产生的力。
作为自然科学历史上的一个重要概念,力偶的研究也得到了广泛
的关注。
在方法论上,物理学家们通常会通过实验和观察来探究力偶
的规律和特性。
同时,理论建模也是力偶研究的重要方式,通过数学
模型来描述力偶的作用和影响。
总之,力偶的概念既有着深厚的历史渊源,又有着广泛的应用领域,它是物理学中的基本概念之一,也是机械设计和工程领域中必不
可少的概念。