_自回归条件异方差模型的研究分析

格式：pdf
大小：193.74 KB
文档页数：6

下载文档原格式

金融风险预测与监测中的自回归条件异方差模型研究

金融风险预测与监测中的自回归条件异方差模型研究金融领域中的风险预测和监测一直都是重要的课题，自回归条件异方差模型（Autoregressive Conditional Heteroskedasticity，简称ARCH模型）在金融风险预测和监测中具有广泛应用的潜力。

本文将探讨金融领域中的风险预测和监测问题，并研究ARCH模型在解决这些问题中的作用。

金融风险预测和监测的目的是为了识别并评估可能对金融市场产生影响的各种风险。

这些风险包括股票价格波动、汇率波动、利率波动等。

了解这些风险对金融市场的影响至关重要，因为它们可能导致投资损失、市场动荡甚至金融危机。

自回归条件异方差模型是由Engle（1982）首先引入的，它被广泛应用于金融风险的建模和预测。

ARCH模型的基本思想是，波动性（volatility）是随时间变化的，并且与之前的波动性存在相关性。

在ARCH模型中，波动性被建模为一个随时间变化的方差序列，这使得我们能够更好地理解金融市场的风险特征。

ARCH模型的核心是建立波动性方程，其中包含了两个重要的部分：一个是自回归项（ARCH项），用于刻画过去波动性对当前波动性的影响；另一个是白噪声项（误差项），用于表示当前波动性的随机部分。

通过估计ARCH模型的参数，我们可以预测未来的波动性，并采取相应的风险管理策略。

在金融风险预测和监测中，ARCH模型有许多优点。

首先，ARCH模型能够捕捉金融市场的波动性特征，对于更好地理解和解释金融市场的波动具有重要意义。

其次，ARCH模型能够提供波动性的预测，帮助投资者和风险管理者制定相应的决策。

此外，ARCH模型的参数估计方法相对简单，计算效率较高。

然而，ARCH模型也存在一些限制。

首先，ARCH模型假设波动性是随时间变化的，但实际中的金融市场波动性可能受到多种因素的影响，包括经济环境、政治因素等。

因此，ARCH模型难以完全捕捉到金融市场波动性的多样性。

其次，ARCH模型基于对波动性方程的参数估计，当样本数据较少或者波动性序列过于复杂时，参数估计的准确性可能受到限制。

自回归条件异方差模型在经济统计学中的应用

自回归条件异方差模型在经济统计学中的应用自回归条件异方差模型（ARCH）是一种经济统计学中常用的时间序列模型，用于分析和预测金融市场波动性。

本文将探讨ARCH模型的应用，以及其在经济统计学中的重要性。

首先，我们来了解一下ARCH模型的基本原理。

ARCH模型是由罗伯特·恩格尔于1982年提出的，用于描述时间序列数据中的异方差性。

在传统的线性回归模型中，假设误差项的方差是恒定的，但实际上，金融市场的波动性往往是不稳定的。

ARCH模型通过引入滞后期的方差来捕捉时间序列数据中的异方差性，从而更准确地描述和预测金融市场的波动性。

ARCH模型的核心思想是，当前时刻的波动性受到过去一段时间内波动性的影响。

具体而言，ARCH模型假设波动性的变化是由过去一段时间内的波动性决定的，而不是由其他因素决定的。

这种模型的优势在于能够捕捉到金融市场中的波动性聚集效应，即波动性在一段时间内呈现出明显的聚集或离散的特征。

ARCH模型的应用非常广泛，尤其在金融领域中发挥着重要的作用。

首先，ARCH模型可以用于金融市场的风险度量和风险管理。

通过对金融资产的波动性进行建模，可以更准确地估计风险水平，为投资者提供更可靠的风险评估指标。

其次，ARCH模型可以用于金融市场的波动性预测。

通过对过去一段时间内的波动性进行建模，可以预测未来的波动性水平，为投资者提供投资决策的参考依据。

此外，ARCH模型还可以用于金融市场的高频交易策略。

通过对短期波动性的建模，可以捕捉到市场中的短期交易机会，实现高频交易的盈利。

除了金融领域，ARCH模型在宏观经济学中也有着重要的应用。

例如，ARCH模型可以用于对宏观经济数据中的波动性进行建模和预测。

通过对经济数据的波动性进行分析，可以更好地理解经济的周期性波动和结构性变化，为宏观经济政策的制定提供参考。

此外，ARCH模型还可以用于对宏观经济风险的度量和管理，为国家和地区的宏观经济政策提供支持。

总之，自回归条件异方差模型在经济统计学中具有重要的应用价值。

广义自回归条件异方差模型(GARCH)在我国股票市场中的实证研究

广义自回归条件异方差模型(GARCH)在我国股票市场中的实证研究广义自回归条件异方差模型（GARCH）是一种在金融领域广泛应用的计量经济学模型，用于描述时间序列数据中的波动性，特别是股票市场中的波动性。

在我国股票市场中，GARCH模型也得到了广泛的应用和研究。

本文通过对我国股票市场中的实证研究，探讨了GARCH模型在描述我国股票市场波动性方面的应用和效果。

一、引言股票市场的波动性一直是投资者和学者关注的焦点之一。

股票市场的波动性会对投资者的投资决策产生重要影响，因此对于股票市场波动性的建模和预测具有重要的意义。

GARCH模型是一种用于描述时间序列数据中波动性的模型，因其简单且有效而在金融领域得到了广泛的应用。

GARCH模型能够捕捉时间序列数据中的波动性特征，对于股票市场的波动性建模具有重要意义。

二、GARCH模型及其在股票市场中的应用GARCH模型由Robert F. Engle于1982年提出，它是对传统的ARCH模型进行了扩展，能够更好地描述时间序列数据中的异方差性。

GARCH模型的基本形式为：\[ y_t = \mu + \varepsilon_t \]\[ \sigma_t^2 = \alpha_0 + \sum_{i=1}^{p} \alpha_i \varepsilon_{t-i}^2 +\sum_{j=1}^{q} \beta_j \sigma_{t-j}^2 \]\( y_t \)为时间序列数据，\( \mu \) 为均值参数，\( \varepsilon_t \) 为误差项，\( \sigma_t \) 为条件标准差，\( z_t \) 为白噪声序列，\( \alpha_i \) 和 \( \beta_j \) 为模型参数，\( p \) 和 \( q \) 为模型阶数。

在股票市场中，GARCH模型常常被用于描述股票收益率的波动性。

股票市场的波动性通常表现为波动性聚集效应，即当市场出现较大波动时，未来仍具有较大的概率会继续出现大的波动，这种特征正是GARCH模型所能较好地捕捉的。

广义自回归条件异方差模型

广义自回归条件异方差模型
以往的条件异方差模型主要是针对于非完全观测的时间序列而提出的，它可以考虑正、负、零值，运用随机比例因子模型将观测值拆分为已知和未知部分。

但是，由于时间序列
非完全观测存在着非常大的误差，条件异方差模型在某些应用场合可能不太适用，因此把
其扩展为广义自回归条件异方差模型（GARCH）是出于这一考虑的。

GARCH模型的基本概念来自于ARMA模型，即假设随机错误穿越时间序列具有一种条件异方差性，异方差可在历
史走势和现有资讯上建模，并不仅仅是与时间序列之前的随机错误有关，还受到时间序列
整体走势的影响。

GARCH模型和普通ARMA模型有可见的不同，其有两个主要模型：GARCH-M（简称M模型）和时间变性GARCH模型（TIGARCH），其中M模型考虑的是单调递增的变量，即以历
史异方差的走势递增的变量，其他还包括对异方差的类型有所限制，考虑的是连续时间序
列中某些特定种类的异方差模型。

TIGARGH模型考虑的是多个时间序列的变量，即以多个
时间序列的异方差水平来表示其变量，以分析其变化情况。

此外，GARCH模型还有一个重要概念，就是共振性，它是指对于潜在低持久性异方差，随机抖动可能会引起变量在某个特定潜在水平上共振，从而产生异常的观测值，这一概念
是Garch模型形成的基础。

最后，总结一下，GARCH模型是一种用于描述非完全观测时间序列的统计模型，它考
虑了时间序列走势的条件异方差和随机抖动引起的共振性，其通过对多个时间序列的变量
进行分析，实现了更精确的计算，这对实证研究和实际应用具有重要意义。

时间序列计量经济学_上_协整和自回归条件异方差模型

第25卷第11期外国经济与管理Vol.25No.11 2003年11月Foreign Economies&Management Nov.2003中图分类号:F270　文献标识码:A　文章编号:100124950(2003)21120039207时间序列计量经济学(上)———协整和自回归条件异方差模型朱小斌　译编者按:今年,瑞典皇家科学院又把诺贝尔经济学奖颁给了计量经济学家美国纽约大学的罗伯特・恩格尔教授和加州大学圣地亚哥分校的克莱夫・格兰杰教授,以表彰他们对时间序列分析作出的重大贡献。

以下是瑞典皇家科学院关于两位获奖者主要理论贡献的介绍。

一、引言宏观经济学和金融经济学中的实证研究很大程度上是以时间序列为基础的。

通过经济学大师Trygve Haavelmo的开创性工作,将经济变量的时间序列视为随机过程现在已经成为了一种标准。

这种方法允许建模者在建立和检验反映经济变量之间关系的方程中使用统计推断。

今年的诺贝尔经济学奖颁给了在以下两方面作出贡献的两位美国经济学家:加深了我们对许多经济变量时间序列非平稳和波动随时间变化这两个基本性质的理解,以及由此引申出的大量实际应用。

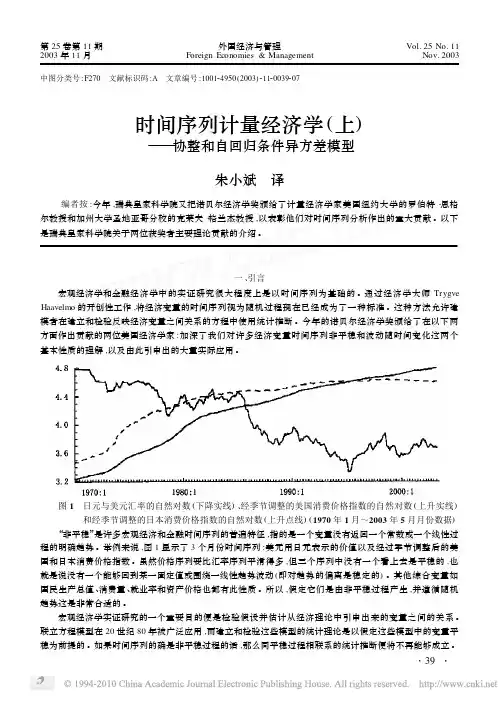
图1　日元与美元汇率的自然对数(下降实线)、经季节调整的美国消费价格指数的自然对数(上升实线)和经季节调整的日本消费价格指数的自然对数(上升点线)(1970年1月～2003年5月月份数据) “非平稳”是许多宏观经济和金融时间序列的普遍特征,指的是一个变量没有返回一个常数或一个线性过程的明确趋势。

举例来说,图1显示了3个月份时间序列:美元用日元表示的价值以及经过季节调整后的美国和日本消费价格指数。

虽然价格序列要比汇率序列平滑得多,但三个序列中没有一个看上去是平稳的,也就是说没有一个能够回到某一固定值或围绕一线性趋势波动(即对趋势的偏离是稳定的)。

其他综合变量如国民生产总值、消费量、就业率和资产价格也都有此性质。

所以,假定它们是由非平稳过程产生,并遵循随机趋势这是非常合适的。

条件异方差模型分析解析

第三节自回归条件异方差(ARCH)模型金融时间序列数据通常表现出一种所谓的集群波动现象。

模型随机误差项中同时含有自相关和异方差。

一、ARCH 模型（Auto-regressive Conditional Heteroskedastic —自回归条件异方差模型）对于回归模型t kt k t t x b x b b y ε++++= 110 （3.3.1）若2t ε服从AR （q ）过程 t q t q t t νεαεααε++++=--221102 （3.3.2）其中tν独立同分布，并满足0)(=t E ν , 2)(σν=tD 则称（3.3.2）式为ARCH 模型，序列t ε服从q 阶ARCH 过程，记为t ε～ARCH （q ）。

(3.3.1)和(3.3.2)称为回归—ARCH 模型。

注：不同时点t ε的方差2)(t t D σε=是不同的。

对于AR （p ）模型t p t p t t y y y εφφ+++=-- 11 （3.3.3）如果tε～ARCH （q ），则（3.3.3）与（3.3.2）结合称为AR （p ）-ARCH （q ）模型。

ARCH （q ）模型还可以表示为 *t t h =εt ν (3.3.4)21022110jt q j q t q t t h -=--∑+=+++=εααεαεααα (3.3.5)其中，tν独立同分布，且0)(=t E ν,1)(=tD ν,00>α 0≥j α)2,1(q j = 且11<∑=q j j α（保证ARCH 平稳）。

有时，（3.3.5）式等号右边还可以包括外生变量，但要注意应保证th 值是非负的。

如：p t p t q t q t t h h h ----++++++=θθεαεαα 1122110 1011<+<∑∑==p j j q i iθα对于任意时刻t ，条件期望E （tε| ,1-t ε）=0)(*=t t E h ν （3.3.6）条件方差t t t t t h E h E ==-)(*),|(2212νεσ （3.3.7）（3.3.7）式反映了序列条件方差随时间而变化。

【生产管理】计量学-向量自回归和自回归条件异方差模型

2
第一节向量自回归模型
一、向量自回归模型概述 ARMA模型分析针对单个时间序列，存在忽略
经济变量之间内在联系的缺点。克服这个缺点的方法是把ARMA模型扩展到针
对多个时间序列，把ARMA模型中的变量换成向量。因为自回归移动平均模型可相互转换，而且在向量变量的情况下自回归模型比较方便，因此一般主要考虑向量变量的自回归模型，称为 “向量自回归模型”（Vector autoregression model，VAR）。
变换成移动平均形式并不是很容易，因此一般采用模拟的方法求向量自回归模型的脉冲——响应函数。令 Yt 1 Yt p c εt 1 εt 2 0
εt (0,,0,1,0,,0)
32
根据上述向量自回归模型模拟时期t、 t+1、t+2…的 Y向量，其中 Yts 即对应矩阵 Ψs 的第j列。让j取遍1,…,n，即可计
7
向量自回归模型VAR(p) 展开，可以写成
每个变量对常数项和向量中所有变量的
1-p阶滞后项回归的，n个方程构成的联
立方程组系统
Y1t
1
Y (1)
11 1,t 1
Y (1)
1n n,t 1
Y ( p)
11 1,t p
Y ( p) 1n n,t p
1t
Ynt
n
Y (1)
21
T
如果
2 i
由其一致估计ˆi2
(1/T )
2 it
T
t 1
代，
而 Q1则由一致估计[(1/T ) XtXt ]1代，则
可以将近似看作
t 1
T
πˆ i ~ N (πi ,[ Xt Xt ]1) t 1
当样本容量较大时，可以利用该渐近分布进行统计推断检验。

实验14 Garch(自回归异方差模型)

实验14 G (ARCH )模型在金融数据中的应用一、实验目的理解自回归异方差（Autoregressive conditional heteroscedasticity ）模型的概念及建立的必要性和适用的场合。

了解G (ARCH ) 模型的各种不同类型，如GARCH-M 模型（GARCH in mean ），EGARCH模型(Exponential GARCH ) 和TARCH模型(又称GJR)。

掌握对G (ARCH )模型的识别、估计即如何运用Eviews软件在实证研究中实现。

二、实验内容及要求内容：以上证指数和深证成份指数为研究对象，选取1997年1月2日到2002年12月31日共六年每个交易日上证指数和深证成份指数的收盘价为样本，完成以下实验步骤：（一）、对沪深股市的收益率作波动性研究（二）、对股市收益波动作非对称性的研究（三）、对沪深股市作波动溢出效应研究要求：深刻理解本章的概念；对实验步骤中提出的问题进行思考；熟练掌握实验的操作步骤，并得到有关结果。

三、实验指导（一）、对沪深股市的收益率作波动性研究1.描述性统计(1)导入数据，建立工作组打开Eviews软件，选择“File”菜单中的“New \Workfile”选项，在“Workfile structure type”框中选择unstructured/undated（思考：为什么用非规则形式），在“Date range”输入1444，如下图14-1：图14-1单击OK ，再在命令行输入data sh sz,把上证综指和深圳成指1997-1-2号到2002-12-31号数据输入。

（2）生成收益率的数据列在Eviews窗口主菜单栏下得命令窗口中键入如下命令：genr rh=log(sh/sh(-1)) ，回车后即形成沪市收益率的数据序列，同样的方法可得深市收益数剧序列(genr rz=log(sz/sz(-1))。

新工作组如图14-2：图14-2（3）观察收益率sh 的描述性统计量双击选取“rh”数据序列，在出现的窗口中选择view 菜单下“Descriptive Statistics”菜单中的“Histogram and Stats”子菜单，则可得收益率rh 的描述性统计量，如下图7-3：图7-3同样的步骤可得收益率rz 的描述性统计量。

异方差回归与自回归模型

异方差回归与自回归模型异方差回归与自回归模型是统计学中常用的两种回归分析模型，它们在预测变量和被解释变量之间关系时都有不同的优势。

异方差回归模型和自回归模型在很多情况下都可以用来拟合数据，但是它们在拟合数据时有一些不同点，这也是它们之间的区别。

一、异方差回归模型异方差回归模型是对线性回归模型的改进，它是一种更强大的统计模型，用于预测两个变量之间的关系，可以更好地描述和预测变量之间的关系。

异方差回归模型是一种可以考虑样本异方差的线性回归模型，主要用于检验两个变量之间是否存在显著的线性关系，所谓“异方差”指的是变量之间的方差不一致，即观察值之间的方差可能随着自变量的变化而变化。

异方差回归模型的应用主要是为了更好地拟合观察数据，使得变量之间的关系更加精确准确，从而更好地描述变量之间的关系，从而更好地预测变量之间的关系。

二、自回归模型自回归模型是一种时间序列模型，它试图通过考察当前变量和其他变量的历史数据来推断当前变量的变化，建立变量之间的关系。

自回归模型将当前变量的值作为另一个变量的函数，从而推断出当前变量的值，而不是直接使用给定的数据进行拟合。

自回归模型有助于我们更好地理解时间序列中变量之间的关系，从而更好地预测这些变量的变化。

自回归模型的优势在于，它可以更好地捕捉时间序列数据之间的长期趋势，从而更好地预测未来的变化趋势。

总结异方差回归模型和自回归模型是两种统计学中常用的回归分析模型，它们在预测变量和被解释变量之间关系时都有不同的优势。

异方差回归模型是一种可以考虑样本异方差的线性回归模型，主要用于检验两个变量之间是否存在显著的线性关系，而自回归模型是一种时间序列模型，它试图通过考察当前变量和其他变量的历史数据来推断当前变量的变化，从而更好地捕捉时间序列数据之间的长期趋势，从而更好地预测未来的变化趋势。

金融市场预测中的自回归条件异方差模型研究

金融市场预测中的自回归条件异方差模型研究第一章：引言金融市场的波动性一直以来都是投资者关注的焦点。

了解和预测金融市场的波动性对于投资决策至关重要。

然而，传统的时间序列分析方法在预测金融市场波动性方面存在一些局限性。

自回归条件异方差模型（Autoregressive Conditional Heteroscedasticity Model, ARCH）的出现为解决这一问题提供了有力的工具。

本章将介绍研究背景、目的和意义，并概述后续章节的内容。

第二章：自回归条件异方差模型的理论基础2.1 自回归模型自回归模型是一种基于时间序列的统计模型，用来描述变量与其自身在不同时点的相关性。

自回归模型具有较好的拟合能力和预测性能，但却无法很好地处理异方差问题。

2.2 异方差模型异方差是指随机变量的方差在不同样本点上发生变化的现象。

传统的回归模型假设误差项的方差是常数，而金融市场中的波动率往往具有时间变化的特点，因此需要引入异方差模型。

2.3 ARCH模型ARCH模型由Engle（1982）提出，通过引入过去的误差项平方来刻画条件异方差性。

ARCH模型以自回归形式描述误差项的方差，并通过最大似然估计方法来估计模型的参数。

第三章：自回归条件异方差模型的应用3.1 风险价值（Value-at-Risk）预测风险价值是衡量金融市场风险程度的一个重要指标，也是金融机构风险管理的核心内容之一。

通过建立ARCH模型，可以对未来一段时间内的风险价值进行预测，从而帮助投资者和金融机构合理配置资产和制定风险管理策略。

3.2 金融市场波动性预测ARCH模型在金融市场波动性预测方面具有广泛应用。

通过建立和估计ARCH模型，可以获得金融市场波动率的动态演化特征，从而为投资者提供有关市场走势和波动性变化的信息。

3.3 交易策略优化利用ARCH模型对金融市场波动性进行预测，可以帮助投资者选择合适的交易策略。

例如，在高波动性时期可以采取较为积极的交易策略，而在低波动性时期则可以采取保守的投资策略，从而降低投资风险。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

· 136 ·
《数量经济技术经济研究》 2006 年第 3 期
一、 ARCH 模型及其参数 α 、 β 的确定
ARCH 模型假设观测数据的方差呈现相关性 , 即观测误差的方差是其滞后值的函数。被预测变量的条件分布为 : yt 其中
T T
Υ t -1 ～ N ( x t β , ht )
T
xt = ( x 1t , x 2 t , …, x n t )
L( θ ) 1 ε t = ∑ S t( θ )= ∑ -1 θ t =1 t =1 2 h t
n
n
2
2 Ln ht 1 ε t θ 2h t θ
T 再对 S t ( θ ) 关于 θ 求导 , 得 t S t( θ ) 1 1 ε = T T 2 ht θ θ 2
Ln ht 1 ε t + -1 θ 2 ht
引言
计量经济学建模时 , 经常会遇到异方差问题 , 在许多应用场合下 , 误差项的方差随时间的变化而变化 ;回归误差的方差依赖于过去误差的变化程度 , 表现出波动的集群性。传统分析中所使用的计量模型 , 如线性回归模型、 A RMA 模型等都采用期望值为零 , 且服从独立同方差的假设 , 不能客观和准确地描述变动的集群性和方差的时变性。自回归条件异方差 ( ARCH ) 模型是由 Ro bert Engle ( 1982) 最早提出的 , 该类模型因其良好的统计特性和对波动现象的准确描述 , 可适用于对经济类时间序列数据 , 诸如股票价格、利率、外汇汇率等的回归分析及预测。近年来虽然关于 A RC H 模型的介绍 ( Krone r , 1992 ;苗实等 , 1999 ; 张世英等 , 2002 ; 王若平 , 2002) 可经常见到 , 但对 A RCH 模型 ( 尤其是多维自回归过程) 的详细计算推导、扰动敏感性的分析以及其在预测股票价格变动中的应用 , 却鲜有报道。
其中
ht y2 t y2 t -1 ] , 则 L 2 ( θ ) = 12 ( 1 +y 2 t -1 ) - 3 ( 1 +y 2 t -1 ) 。 T = [1 θ 2h t ht λ 1 , Cm in =
T T
在加入扰动后的 A RCH 模型中 , 最大、最小曲率仍然分别为 Cm ax =2 2
2 2 2 ht =h ( ε t -1 , ε t -n , …, ε t -p , α ) ht =α 0 +α 1ε t -1 +α 2ε t -2 +… + α mε t -m
α =( α 0 , α 1 , …, α m) β= ( β1 , β2 , … , βn) ε t = y t -x t β Υ t 是在 t 时刻的信息集合 , x t 是一些外生变量或被预测变量的滞后值构成的向量 , 以其中 m 项观察为条件 ( t1 , t -2 , …, t m) , 用 n 项观察来估计 ( 1t , 2 t , …, nt) ;α 、 β 是待定参数。其中误差项服从均值为 0 、方差为 ht 的正态分布 , 即 ε t ～ N ( 0 , ht ) , 也就是说 f ( yt 令则 f ( yt
自回归条件异方差模型的研究分析
· 135 ·
自回归条件异方差模型的研究分析
王立凤
1 、2
陆晓倩
1 、2
( 1 .厦门大学经济学院 ;2.集美大学工商管理学院)
【摘要】自回归条件异方差 ( ARCH ) 模型适用于对具有群集性和方差时变性特点的经济类时间序列数据的回归分析和预测。本文对 ARCH 模型中待定参数的确定进行了详细推导 ; 探讨了对 ARCH 模型扰动影响的敏感性进行分析计算的方法 ; 并实例应用 ARCH 模型对股票收盘价格的全年变动进行预测 , 研究分析其特点。关键词 A RCH 模型预测方差扰动影响股价中图分类号 F 832. 51 文献标识码 A
ω ) ∑ L n(
t
而利用 L1 ( θ ) 、 L2 ( θ ) 就可以求出局部影响的曲率度量 , 从而判断 A RC H 模型估计的误差度 ( 即模型的风险大小) 。在 ARCH 模型中 , 最大最小曲率分别为 Cm ax =2 λ 1 , Cm in =2 λ 2 , 其中 λ 1 、 λ 2 分 T T 别为矩阵 G L 2 ( θ ) G =Δ L 2 ( θ ) Δ中绝对值最大和最小的特征值。其中 ( ω ) G = θ Δ = ω
在 ARCH 模型中的参数估计是基于似然函数的 , 因而可以假设对模型的扰动就是对似然函数的扰动 ( 即假设直接影响 h t ) 。 L( θ ( ω ) )=- 1 2 2π h t )- 1 ∑ L n( 2 t =1
n 2 ( y - xT t β) +1 ∑ ht 2 t =1 n n t =1
2 1 Lnht 1 ε t ht 1 ε t T = 2ε t xt -2 T + 1 2 θ ht ht θ 2 ht
2x t x t 0 2ε txt Lnht 1 1 ht + T T θθ 2ht 2 h2t θ 0 0 0
T
二、 ARCH 模型扰动影响的计算分析
2
L( θ ) θω
若最大曲率较小 , 则说明模型的风险较小 ; 若最小曲率较大 , 则说明模型的风险较大。则 1 1 1 1 y2 t L1 ( θ ) =+ 2 2 2 2h t y t -1 2 h t y t -1
1 θ y2 t ht 1 )= 1 h t 1 L2 ( θ )= L ( - 3 T 2 T T θ 2 ht θ y t -1 h t θ y t -1
将式 ( 3) 、( 4) 结果代入式 ( 2) 得
m
1 +ε St ( θ )= 2h t 2h2t 则 L1( θ )=
2 t
j =1
ε x ∑ -2 α
j tj
t -j
ξ t( β)
xt u t 2 L( θ ) 1 ε t + ht = = -1 θ 2 ht 0
2 Ln ht 1 ε t θ 2 ht θ
ARCH 模型对扰动影响的局部敏感性。将扰动因素表示为 :
T T ω =( ω 1 , ω 2 , …, ω p)
按照局部影响的定义 , 定义似然距离 LD ( ω )= 2 [L ( θ ) -L ( θ( ω ) ) ] , 其中 θ 为不存在扰动时对 θ 的估计 , 而 θ( ω ) 为对摸型加入扰动后的估计 , 则 LD ( ω ) 反映了扰动对模型的影响。相应地 , 一个好的模型 , 它受扰动的影响应该较小。 Z =L D ( ω ) 为影响图 , 表示一个 p +1 维空间的 p 维曲面 , 反映了扰动对模型的影响。在这个空间 , 过 ω 0 做方向为 d 的曲线 , L d ∶η d ( t) =ω 0 + dt , 则过 ω 0 方向为 d 的曲线的曲率和最大最小曲率分别为 : Cd = ‖η 2d ‖ 2 Cm ax =‖ max Cd Cm in =‖min Cd d ‖ =1 d ‖ =1 ‖η 1d ‖
n
∏
( y -x t β) 1 ex p 2h t 2π ht
n t =1
T
2
=- n L n( 2π )- 1 2 2
ht )- 1 ∑ L n( 2 t =1
∑
2 ( y - x tT β) ht
采用极大似然估计法就是固定样本的观察值 , 在 θ 可能的区间内挑选出使概率 L ( θ ) 最大的参数值 θ , 估计出待定参数 α 、 β。
n
L( θ ) = θ = 令 St ( θ ) =
Ln
t =1
y ∏f (
t
|Υ t1 ; θ ) ( 1)
θn t =1∑Fra bibliotek-1 2
2 2 L n( ht ) 1 1 ( y - x tT β) ( y - xT t β) h t 2 θ 2 ht θ ht θ
Ln f( yt
t -1 ; Υ θ ) 1 L n( ht ) 1 1 ( y -x t β) ( y -x t β) h t =θ 2 θ 2 ht θ h2 t θ
m
2 ε t -j θ
0 0n = 1 0 0 其中 +
0 0n 0
2 ε t1
0 0n +…+ 0 0
t-m ε 2 m
-2ε t -j x t -j + ∑α j
j =1
m
0 0
=
j =1
∑ -2ε x
tj
tj
ξ t( β)
0
2 2 2 T ξ t ( β) = [ 1 , ε t -1 , ε t -2 , …, ε t -m ]
T
2
T
2
( 2)
自回归条件异方差模型的研究分析
· 137 ·
其中
T 2 -2 x t ε t ( y -x t β) = θ 0( m项) 2 2 2 ht ( α 0 +α 1ε t-1 +α 2ε t2 + … +α mε t -m ) = = θ θ
( 3)
m
α 0 + θ j∑ =1
α j 2 ε t -j + j ∑α θ j =1
t -1) = Υ T
T
1 ( y -x t β) exp 2 ht 2π ht
T T
T
2
θ =( β , α) Υ t -1 ; θ )=
2 1 ( y -x tT β) ex p 2h t 2π ht
由极大似然估计法可得样本的似然函数