第三讲+条件异方差模型

时间序列条件异方差模型时间序列分析是一种重要的统计分析方法，用于研究时间变量之间的关系。

在金融、经济学、气象学和其他领域，时间序列分析都扮演着重要的角色。

而条件异方差模型则是一种用于捕捉时间序列数据中异方差性质的模型。

本文将介绍时间序列条件异方差模型的概念、原理、应用以及在金融领域的重要性。

一、条件异方差模型的概念条件异方差模型，全称为条件异方差自回归移动平均模型（ARCH），是由Robert F. Engle于1982年提出的一种用于描述时间序列数据中异方差性质的模型。

它认为时间序列数据中的方差是随时间变化的，并受到之前残差的影响，即当前的方差是过去残差的函数。

而在实际应用中，ARCH模型的延伸GARCH模型则是被广泛使用的一种工具，它不仅可以捕捉时间序列数据中的异方差性质，还可以考虑到长期记忆性和其他特征。

二、条件异方差模型的原理条件异方差模型的原理在于将时间序列数据的方差建模为过去残差的函数。

以GARCH(1,1)模型为例，其方差可以表示为：σ^2_t = ω + αε^2_(t-1) + βσ^2_(t-1)其中，σ^2_t为时间t的方差，ω为模型中的常数项，α和β分别表示过去残差和过去方差的权重。

这个模型说明当前的方差受到上一个时期残差的影响，而且方差是随时间变化的。

通过对时间序列数据进行拟合，可以得到最优的α、β和ω参数，从而建立条件异方差模型。

三、条件异方差模型的应用条件异方差模型在金融领域得到了广泛的应用。

由于金融市场的波动性较高，时间序列数据中经常存在着异方差性质。

而条件异方差模型可以帮助金融从业者更好地理解和预测市场的波动性，从而做出更为准确的决策。

例如，投资者可以利用条件异方差模型对金融资产的风险进行度量和管理，而交易员可以利用该模型进行波动性的预测和交易策略的制定。

四、条件异方差模型在金融领域的重要性金融时间序列数据中的异方差性质是一个重要的问题。

大量的实证研究表明，金融资产的收益率往往表现出高度的异方差性，这给投资者和决策者带来了很大的挑战。

条件异方差模型
条件异方差模型(ConditionalHeteroskedasticityModels，CHM)是一种用来检验和处理数据中异方差（heteroskedasticity）问题的模型，旨在估计和检验观测数据中异方差的存在，以及其影响程度，来获得更准确的分析结果。

条件异方差模型可分为简单异方差模型和动态异方差模型。

简单异方差模型假设观测值有固定的异方差，而动态异方差模型则假设异方差可以动态变化。

异方差模型通常包括四个步骤：
（1）数据准备：首先，将数据转换为异方差模型可识别的数据格式，其中可能包括数据集的统计量，如平均值，方差，偏度，峰度等；
（2）模型拟合：使用统计模型拟合数据，用于预测观测值的异方差；
（3）异方差识别：利用拟合的模型，采用检验的方法来识别异方差的存在；
（4）异方差处理：对于经识别的异方差，采用最优化的处理办法，以获得更准确和实用的异方差分析结果。

由于条件异方差模型提供了一种有效的方法来理解和处理异方差，因此，它在许多学科中，如财务分析，统计分析，市场营销，投资管理，经济分析等领域中被广泛应用。

- 1 -。

条件异方差模型分析解析第三节自回归条件异方差(ARCH)模型金融时间序列数据通常表现出一种所谓的集群波动现象。

模型随机误差项中同时含有自相关和异方差。

一、ARCH 模型（Auto-regressive Conditional Heteroskedastic —自回归条件异方差模型）对于回归模型t kt k t t x b x b b y ε++++= 110 （3.3.1）若2t ε服从AR （q ）过程t q t q t t νεαεααε++++=--221102 （3.3.2）其中tν独立同分布，并满足0)(=t E ν , 2)(σν=tD 则称（3.3.2）式为ARCH 模型，序列t ε服从q 阶ARCH 过程，记为t ε～ARCH （q ）。

(3.3.1)和(3.3.2)称为回归—ARCH 模型。

注：不同时点t ε的方差2)(tt D σε=是不同的。

对于AR （p ）模型t p t p t t y y y εφφ+++=-- 11 （3.3.3）如果tε～ARCH （q ），则（3.3.3）与（3.3.2）结合称为AR （p ）-ARCH （q ）模型。

ARCH （q ）模型还可以表示为 *t t h = εt ν (3.3.4) 21022110j t q j q t q t t h -=--∑+=+++=εααεαεααα (3.3.5)其中，tν独立同分布，且0)(=t E ν,1)(=t D ν,00>α 0≥j α)2,1(q j = 且11<∑=q j j α（保证ARCH 平稳）。

有时，（3.3.5）式等号右边还可以包括外生变量，但要注意应保证th 值是非负的。

如：p t p t q t q t t h h h ----++++++=θθεαεαα 1122110 1011<+<∑∑==p j j q i iθα对于任意时刻t ，条件期望E （tε| ,1-t ε）=0)(*=t t E h ν （3.3.6）条件方差t t t t t h E h E ==-)(*),|(2212νεσ （3.3.7）（3.3.7）式反映了序列条件方差随时间而变化。

计量经济学：异方差性异方差性在现实经济活动中，最小二乘法的基本假定并非都能满足，上一章介绍的多重共线性只是其中一个方面，本章将讨论违背基本假定的另一个方面——异方差性。

虽然它们都是违背了基本假定，但前者属于解释变量之间存在的问题，后者是随机误差项出现的问题。

本章将讨论异方差性的实质、异方差出现的原因、异方差的后果，并介绍检验和修正异方差的若干方法。

第一节异方差性的概念一、异方差性的实质第二章提出的基本假定中，要求对所有的i （i=1，2，…，n ）都有2)(σ=i u Var （5.1）也就是说i u 具有同方差性。

这里的方差2σ度量的是随机误差项围绕其均值的分散程度。

由于0)(=i u E ，所以等价地说，方差2σ度量的是被解释变量Y 的观测值围绕回归线)(i Y E =ki k i X X βββ+++ 221的分散程度，同方差性实际指的是相对于回归线被解释变量所有观测值的分散程度相同。

设模型为n i u X X Y iki k i i ,,2,1221 =++++=βββ （5.2）如果其它假定均不变，但模型中随机误差项i u 的方差为).,,3,2,1(,)(22n i u Var i i ==σ (5.3)则称i u 具有异方差性。

由于异方差性指的是被解释变量观测值的分散程度是随解释变量的变化而变化的，如图5.1所示，所以进一步可以把异方差看成是由于某个解释变量的变化而引起的，则)()(222i i i X f u Var σσ== (5.4)图5.1二、产生异方差的原因由于现实经济活动的错综复杂性，一些经济现象的变动与同方差性的假定经常是相悖的。

所以在计量经济分析中，往往会出现某些因素随其观测值的变化而对被解释变量产生不同的影响，导致随机误差项的方差相异。

通常产生异方差有以下主要原因：1、模型中省略了某些重要的解释变量异方差性表现在随机误差上，但它的产生却与解释变量的变化有紧密的关系。

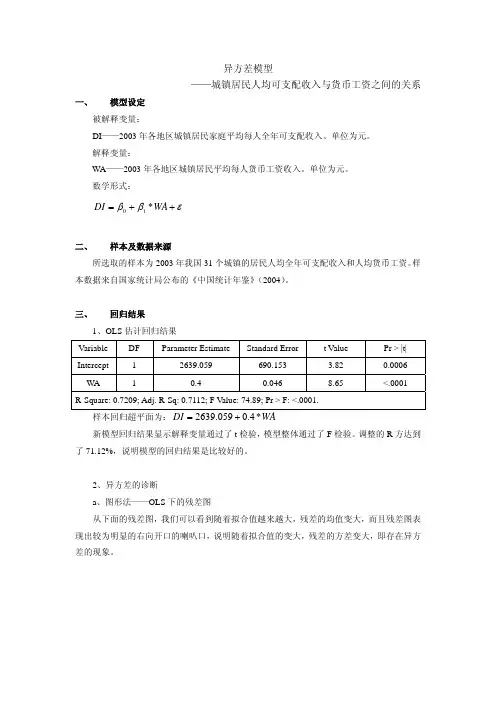
异方差模型——城镇居民人均可支配收入与货币工资之间的关系一、模型设定 被解释变量：DI ——2003年各地区城镇居民家庭平均每人全年可支配收入。

单位为元。

解释变量：WA ——2003年各地区城镇居民平均每人货币工资收入。

单位为元。

数学形式：εββ++=10WA DI *二、样本及数据来源所选取的样本为2003年我国31个城镇的居民人均全年可支配收入和人均货币工资。

样本数据来自国家统计局公布的《中国统计年鉴》（2004）。

三、回归结果1、OLS 估计回归结果 VariableDFParameter EstimateStandard Error t Value Pr > |t| Intercept 1 2639.059 690.153 3.820.0006WA 10.40.0468.65 <.0001R-Square: 0.7209; Adj. R-Sq: 0.7112; F Value: 74.89; Pr > F: <.0001.样本回归超平面为：WA DI *4.0059.2639+=新模型回归结果显示解释变量通过了t 检验，模型整体通过了F 检验。

调整的R 方达到了71.12%，说明模型的回归结果是比较好的。

2、异方差的诊断a 、图形法——OLS 下的残差图从下面的残差图，我们可以看到随着拟合值越来越大，残差的均值变大，而且残差图表现出较为明显的右向开口的喇叭口，说明随着拟合值的变大，残差的方差变大，即存在异方差的现象。

70008000900010000110001200013000-4000-200002000Fitted values R e s i d u a l slm(a$DI ~ a$WA)Residuals vs Fitted261129b 、White 检验利用White 检验的结果如下表所示Heteroscedasticity TestEquation Test Statistic DF Pr> ChiSq Variables DI White's Test12.9420.0016Cross of all varsWhite 检验的结果同样说明了异方差的存在，检验的P 值为0.0016，在1%的水平上能够通过显著性检验。

条件异方差模型条件异方差模型是一种用于描述时间序列数据的统计模型，它考虑到了不同时间点上的方差可能是不同的。

这种模型可以用来分析股票价格、汇率等金融数据，也可以用来分析环境变量、气象数据等自然科学数据。

在条件异方差模型中，方差是一个随时间变化的函数，通常被称为条件方差。

这意味着，在给定一些先前观察到的数据之后，我们可以预测未来观测值的方差。

这种方法比传统的线性回归模型更加准确，因为它能够捕捉到随着时间推移而发生变化的不确定性。

条件异方差模型最常见的形式是ARCH（自回归条件异方差）和GARCH（广义自回归条件异方差）模型。

ARCH模型是一种基于过去观测值的平方误差来预测未来观测值误差方差的模型。

GARCH模型则扩展了ARCH模型，并允许过去多个时间点上的平方误差对当前观测值误差方差产生影响。

在实际应用中，我们通常使用最小二乘法或极大似然估计法来拟合条件异方差模型。

最小二乘法是一种通过最小化残差平方和来确定模型参数的方法，而极大似然估计法则是一种基于观测到的数据来估计未知参数的方法。

需要注意的是，条件异方差模型并不适用于所有类型的时间序列数据。

例如，在具有周期性变化或季节性变化的数据中，方差通常是稳定的，因此不需要使用条件异方差模型。

此外，在具有明显趋势或趋势突变的数据中，也可能需要使用其他类型的时间序列模型。

总之，条件异方差模型是一种强大而灵活的统计工具，可以用于分析各种类型的时间序列数据。

它能够捕捉到随着时间推移而发生变化的不确定性，并且可以通过最小二乘法或极大似然估计法来拟合模型参数。

但需要注意，它并不适用于所有类型的时间序列数据，并且在实际应用中需要谨慎选择合适的模型。

条件异方差模型介绍条件异方差模型是一种用于建模和分析时间序列数据的统计模型。

在时间序列分析中，我们通常假设序列的方差是恒定的，即服从同方差假设。

然而，在实际应用中，我们经常遇到方差不恒定的情况，这时就需要使用条件异方差模型。

什么是条件异方差条件异方差指的是时间序列数据的方差在不同条件下发生变化。

换句话说，条件异方差模型允许我们在建模过程中考虑方差的非恒定性。

这在金融领域特别常见，因为金融数据通常具有波动性较大的特点。

条件异方差模型的应用条件异方差模型在金融风险管理、投资组合优化、期权定价等领域都有广泛的应用。

通过考虑方差的非恒定性，条件异方差模型能够更准确地捕捉到金融市场的波动性，从而提高模型的预测能力和风险控制能力。

常见的条件异方差模型ARCH模型ARCH（Autoregressive Conditional Heteroskedasticity）模型是最早被提出的条件异方差模型之一。

ARCH模型假设序列的方差是过去方差的线性函数，并且具有自回归结构。

ARCH模型的一阶形式可以表示为：2σt2=α0+α1ϵt−12是时间点t-1的残差的平其中，σt2是时间点t的方差，α0和α1是模型的参数，ϵt−1方。

GARCH模型GARCH（Generalized Autoregressive Conditional Heteroskedasticity）模型是对ARCH模型的拓展，能够更好地捕捉到方差的非恒定性。

GARCH模型引入了条件方差的滞后项，并且具有自回归滑动平均结构。

GARCH模型的一阶形式可以表示为：σt2=α0+∑αipi=1ϵt−i2+∑βjqj=1σt−j2其中，α0,α1,...,αp和β1,β2,...,βq是模型的参数，p和q分别表示条件方差和滞后项的阶数。

EGARCH模型EGARCH（Exponential GARCH）模型是对GARCH模型的改进，能够更好地对称和非对称的影响进行建模。