材料力学 第二章 轴向拉压、剪切挤压
- 格式:doc
- 大小:10.09 MB
- 文档页数:18


第2章拉伸压缩与剪切教学目的:了解材料的力学性质;掌握轴向拉伸、压缩、剪切和挤压的概念;掌握轴向拉压时构件的内力、应力、变形的计算;熟练掌握剪切应力及挤压应力的计算方法并进行强度校核;掌握拉压杆的超静定问题。
教学重点:建立弹性杆件横截面上内力、内力分量的概念;运用截面法画轴力图;掌握低碳钢的力学性质;掌握轴向拉伸和压缩时横截面上正应力计算公式及其适用条件;掌握拉压杆的强度计算;熟练掌握剪切和挤压的实用计算。
教学难点:低碳钢类塑性材料在拉伸过程中反映出的性质;许用应力的确定和使用安全系数的原因;强度计算问题;剪切面和挤压面的确定;剪切和挤压的实用计算;拉压杆超的静定计算。
教具:多媒体。
教学方法:采用启发式教学,通过提问,引导学生思考,让学生回答问题。
举例掌握轴向拉伸、压缩和剪切变形概念,通过例题、作业,加强辅导熟练运用截面法,掌握轴力图的画法;建立变形、弹性变形、应变、胡克定律和抗拉压刚度的概念;教学内容:轴向拉伸和压缩的概念;强度计算;材料的力学性能及应力应变图;许用应力与安全系数;超静定的计算;剪切概念;剪切实用计算;挤压实用计算。
教学学时:8学时。
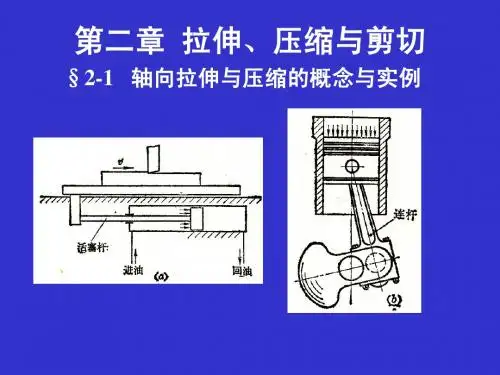
教学提纲:2.1 轴向拉伸与压缩的概念和实例1.实例(1)液压传动中的活塞杆(2)内燃机的连杆(3)起吊重物用的钢索(4)千斤顶的螺杆(5)桁架的杆件2.概念及简图这些杆件虽然外形各异,受力方式不同,但是它们有共同的特点:(1)受力特点:作用在杆件上的外力合力的作用线与杆件轴线重合,杆件变形是沿轴线方向的伸长或缩短。
(如果两个F 力是一对离开端截面的力,则将使杆发生纵向伸长,这样的力称为轴向拉力; 如果是一对指向端截面的力,则将使杆发生纵向缩短,称为轴向压力)。
(2)变形特点:主要变形是纵向伸长或缩短。
(3)拉(压)杆的受力简图:(4)说明:本章所讲的变形是指受压杆没有被压弯的情况下,不涉及稳定性问题。
2.2 轴向拉伸或压缩时横截面上的内力和应力1.截面法求内力(1)假想沿m-m 横截面将杆切开(2)留下左半段或右半段(3)将弃去部分对留下部分的作用用内力代替(4)对留下部分写平衡方程,求出内力(即轴力)的值。








第一部分 作轴力图2-1c 试求图示各杆1-1 2-2 3-3 截面上的轴力,并作轴力图。
(b ')(c ')F N 1(d ')解:方法一:截面法(1)用假想截面将整根杆切开,取截面的左或右边为研究对象,受力如图(b)、(c)、(d)所示。
列平衡方程求轴力: (b) 图:110000xN N F F F =→-=→=∑ (c) 图:220404()xN N FF F F F =→-=→=∑拉 (d) 图:330303()xN N FF F F F =→-=→=∑拉(2)杆的轴力图如图(e )所示。
方法二:悬臂法。
(为方便理解起见,才画出可以不用画的 (b ‘)、(c ‘)、(d ‘) 图,)作题的时候可用手蒙住丢弃的部份,并把手处视为“固定端”,指向“手固定端”的力引起负的轴力,反之引起正的轴力) (1)因为轴力等于截面一侧所有外力的代数和:N F F=∑一侧。
故:10N F = 24()N F F =拉 33()N F F =拉(2)杆的轴力图如图(e )所示。
方法三:动点轨迹方法。
根据杆件的平衡求出杆左端的约束反力为4F 。
从左到右画轴力图,凡是向左的力轴力图向上突变(轴力值增大),向右的力轴力图向下突变(轴力值变小),即左上右下,突变之值是该处集中力的大小,轴力图从零开始最后回归到零。
补充1: 试画求图示各杆的轴力图。
(c ')(e ')(d ')(kN)20455(f)(kN)205455(f ')题5-1aF NF N解:方法一:截面法(1)用假想截面将整根杆切开,取截面的右边为研究对象,受力如图(b)、(c)、(d)、(e)所示。
列平衡方程求轴力: (b) 图:11020020()xN N F F F kN =→-=→=∑拉(c) 图:2202025020255()xN N FF F kN =→--=→=-=-∑压(d) 图:330202550020255045()xN N F F F kN =→-+-=→=-+=∑拉 (e) 图:440202550400202550405()xN N FF F kN =→-+--=→=-+-=∑拉(2)杆的轴力图如图(f )所示。
方法二:悬臂法。
(为方便理解起见,才画出可以不用画的 (b ‘)、(c ‘)、(d ‘)、(e ‘) 图,作题的时候可用手蒙住丢弃的部份,并把手处视为“固定端”,指向“手固定端”的力引起负的轴力,反之引起正的轴力) (1)因为轴力等于截面一侧所有外力的代数和:N F F=∑一侧。
故:120()N F kN =拉220255()N F kN =-=-压 320255045()N F kN =-+=拉4202550405()N F kN =-+-=拉(2)杆的轴力图如图(f ‘)所示。
方法三:动点轨迹方法。
根据杆件的平衡求出杆左端的约束反力为5kN 。
从左到右画轴力图,凡是向左的力轴力图向上突变(轴力值增大),向右的力轴力图向下突变(轴力值变小),即左上右下,突变之值是该处集中力的大小,轴力图从零开始最后回归到零。
F (kN)(f ')45PF N 图(d)题2-1c补充2:作图示杆的轴力图。
解:(1)用1-1截面将整个杆切开,取左边部分为研究对象;再用x -x 截面整个杆切开,取右边部分为研究对象,两脱离体受力如图(b)、(c),建立图示坐标。
(2)列平衡方程求杆的轴力(c)图:(b)图:(3)杆的轴力图如图(d )所示。
第二部分 求拉压杆应力2-2 作用于零件的拉力F =38kN ,试问零件的最大应力发生于哪个截面上?并求其值 ·()1100()0/2x N N F F P F P x l =→-=→=<<∑拉()0(/2)0(/2)()/23/2xN x N x Fq x l F F q x l l x l =→--=→=-<<∑拉题2.2图解:轴力均为F =38kN331-12-21-12-21-12-23810381063.3347.520.0150.02(0.050-0.01)0.02N N F F A A σσ⨯⨯=====⨯⨯⨯Pa MPa >Pa =MPa33-33-33-3381045.242(0.050-0.022)0.015N F A σ⨯===⨯⨯Pa MPa2-5 图示结构中,1、2杆的截面直径分别为10mm 和20mm ,试求两杆内的应力。
设两根横梁皆为刚体。
解:(1)AB 杆相当于连杆,F D =0。
视销钉与ABC 固结,研究ABC 受力如图所示,1、2杆为受拉的二力杆。
22211()01102020100100C ym F F F F F F F ⎧=⨯-⨯==⎧⎧⎪→→⎨⎨⎨--===⎩⎩⎪⎩∑∑kNkN (2)求两杆应力331212221210102010127.3263.670.0100.02044N N F F A A σσππ⨯⨯=====⨯⨯Pa MPaPa =MPa2-6 直径为10mm 的圆杆,在拉力F=10kN 的作用下,试求最大切应力,并求与横截面的夹角为α=30o的斜切面上的正应力及切应力。
解:(1)应力求横截面的应力3021010127.320.0104N F A σπ⨯===⨯Pa MPa(2)求最大切应力max 127.32sin 2222ασστατ=→===63.66MPa (3)求与横截面的夹角为α=30o 的斜切面上的正应力及切应力。
220cos 127.32cos 30ασσα===95.4MPa127.32sin 2sin 6022αστα===55.13MPa补充3 图示两根截面为100mm ⅹ100mm 的木柱,分别受到由横梁传来的外力作用。
试计算两柱上、中、下三段的应力。
(b)(c)(d)(f)题5-2-N 图(kN)6108.5326.5-N 图(kN)梁与柱之间通过中间铰,可视中间铰为理想的光滑约束。
将各梁视为简支梁或外伸梁,柱可视为悬臂梁,受力如图所示。
列各梁、柱的平衡方程,可求中间铰对各梁、柱的约束反力,计算结果见上图。
(2)作柱的轴力图,如(e)、(f)所示。
(3)求柱各段的应力。
333336103100.60.30.010.010.010.01101021010.20.010.010.010.018.5100.850.010.01N AB N EF AB EF N BC N FG BC FG N CD N GH CD GH F F Pa MPa Pa MPa A A F F Pa MPaPa MPa A A F F Pa MPa A A σσσσσσ⎧-⨯-⨯===-===-⎪⨯⨯⎪-⨯-⨯⎪===-===-⎨⨯⨯⎪⎪-⨯===-==⎪⨯⎩左柱右柱36.5100.650.010.01Pa MPa ⎧⎪⎪⎪⎨⎪⎪-⨯=-⎪⨯⎩第三部分 拉压强度2-8汽车离合器踏板如图所示。
已知踏板受到压力F 1=400 N 作用,拉杆1的直径D=9mm ,杠杆臂长L =330 mm ,L =56 mm 拉杆的许用应力[]50MPa σ=。
校核1拉杆的强度。
解:(1)研究杠杆受力如图所示,列平衡方程求1拉杆所受拉力1122400330()002357.1456A F L mF F L F l F l ⨯⨯=→⨯-⨯=→===∑N N (2) 校核1拉杆的强度[]22237.05500.0094235714.4N F F A D σσππ=====Pa M Pa<M Pa 故:1杆的拉压强度足够。
2.9冷镦机的曲柄滑块机构如图所示。
镦压工件时连杆接近水平位置,承受的压镦力F =1100 kN 。
连杆是矩形截面,高度h 与宽度b 之比为:1.4hb=。
材料为45钢,许用应力[]58MPa σ=。
试确定截面尺寸h 及b 。
解:按轴向拉压强度确定截面尺寸h 及b[]336621100101581.41100104110.580N F F b A bh b σσ==⨯⨯⨯⨯⨯==→>m =0.1164m =116.4mm Pa<Pa 取b =117mm ,则h b =⨯≈=1.4 1.4116.4=162.96163mm2.12 在简易吊车中,BC 杆为钢杆,AB 杆为木杆。
木杆AB 的横截面积21100A =cm ,许用应力[]17MPa σ=;钢杆BC 的横截面积226A =cm ,许用应力[]2160MPa σ=。
试求许可吊重F 。
CA30°B FFB30°题2.11图木钢A 2 [σ2]A 1 [σ1]F N 1F N 2解:方法一:(1)求杆件的容许轴力[F N ][][]6441117101001071070N F A σ-=⨯=⨯⨯⨯=⨯=N kN[][]64322216010610961096N F A σ-=⨯=⨯⨯⨯=⨯=N kN(2)求出内力F N 与F 的关系,研究节点,受力如图:2221102()sin 3000cos3003()y N N x N N N F F F F F F F F F F ⎧==⎧⎧-=⎪⎪⎪→→⎨⎨⎨=--==-⎪⎪⎪⎩⎩⎩∑∑拉压 (3)由强度条件确定F :1122[]7040.440.4482[]96N N N N F F F F F F F F ⎧=≤=≤⎧⎪→→≤⎨⎨≤=≤=⎩⎪⎩kN kNkN kN kN故,结构的容许荷载[]40.4P =kN方法二:(1)求出内力F N 与F 的关系,研究节点,受力如图:2221102()sin 3000cos300()y N N x N N N F F F F F F F F F ⎧==⎧⎧-=⎪⎪⎪→→⎨⎨⎨=--==⎪⎪⎪⎩⎩⎩∑∑拉压 (2)由强度条件确定F :6114162242[]710Pa 40.41001040.4482[]16010Pa 610N N F F A F F F F A σσσσ--⎧⎪===≤=⨯≤⎧⎪⨯→→≤⎨⎨≤⎩⎪==≤=⨯⎪⨯⎩kN kN kN 故,结构的容许荷载[]40.4P =kN补充4:图示三角架中,已知:[][]MPa ,A MPa A 100900,160,6002211====σσ22mm mm ,试求结构的许可荷载[P ]。
解:方法一:(1)求杆件的容许轴力[F N ][][]6611116010600109600096N F A N σ-=⨯=⨯⨯⨯==kN[][]6622210010900109000090N F A N σ-=⨯=⨯⨯⨯==kN(2)求出内力F N 与P 的关系,研究节点,受力如图(b): 由于结构对称,荷载对称,所示F N 1=F N 211202cos0()6yN N N FF P F F P π=→-=→==∑拉(3)由强度条件确定P :112296[]969090[]90N N N N P kN F P F kNP kN P kN F P F kN⎧≤=≤=⎧⎪→→≤⎨⎨≤=≤=⎪⎩⎩ 故,结构的容许荷载[]kN 90=P 方法二:(略)补充5:已知图中结构的横梁AB 为刚体,①、②两杆的材料相同,许用应力均为[]160MPa σ=,杆①的横截面积A 1=20cm 2,杆②的横截面积A 2=12cm 2。