材料力学002第二章轴向拉压与剪切

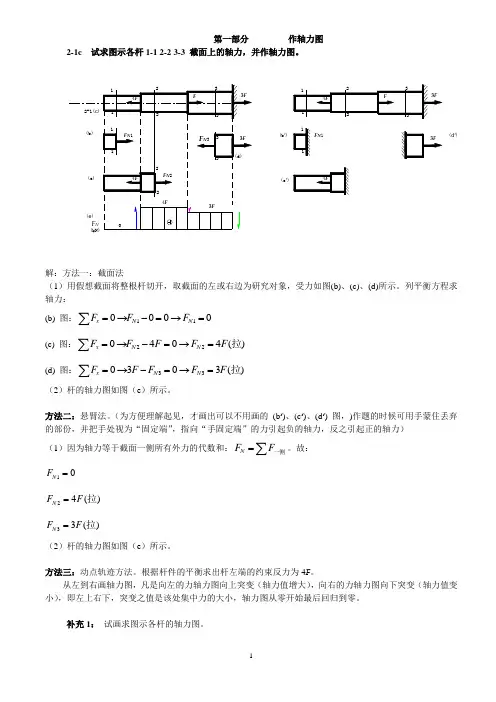
第一部分 作轴力图2-1c 试求图示各杆1-1 2-2 3-3 截面上的轴力，并作轴力图。

(b ')(c ')F N 1(d ')解：方法一：截面法（1）用假想截面将整根杆切开，取截面的左或右边为研究对象，受力如图(b)、(c)、(d)所示。

列平衡方程求轴力： (b) 图：110000xN N F F F =→-=→=∑ (c) 图：220404()xN N FF F F F =→-=→=∑拉 (d) 图：330303()xN N FF F F F =→-=→=∑拉（2）杆的轴力图如图（e ）所示。

方法二：悬臂法。

（为方便理解起见，才画出可以不用画的 (b ‘)、(c ‘)、(d ‘) 图，)作题的时候可用手蒙住丢弃的部份，并把手处视为“固定端”，指向“手固定端”的力引起负的轴力，反之引起正的轴力） （1）因为轴力等于截面一侧所有外力的代数和：N F F=∑一侧。

故：10N F = 24()N F F =拉 33()N F F =拉（2）杆的轴力图如图（e ）所示。

方法三：动点轨迹方法。

根据杆件的平衡求出杆左端的约束反力为4F 。

从左到右画轴力图，凡是向左的力轴力图向上突变（轴力值增大），向右的力轴力图向下突变（轴力值变小），即左上右下，突变之值是该处集中力的大小，轴力图从零开始最后回归到零。

补充1： 试画求图示各杆的轴力图。

(c ')(e ')(d ')(kN)20455(f)(kN)205455(f ')题5-1aF NF N解：方法一：截面法（1）用假想截面将整根杆切开，取截面的右边为研究对象，受力如图(b)、(c)、(d)、(e)所示。

列平衡方程求轴力： (b) 图：11020020()xN N F F F kN =→-=→=∑拉(c) 图：2202025020255()xN N FF F kN =→--=→=-=-∑压(d) 图：330202550020255045()xN N F F F kN =→-+-=→=-+=∑拉 (e) 图：440202550400202550405()xN N FF F kN =→-+--=→=-+-=∑拉（2）杆的轴力图如图（f ）所示。

第2章 拉伸、压缩与剪切1、轴向拉伸与压缩概念：作用于杆件上的外力合力的作用线与杆件轴线重合，杆件变形是沿轴线方向的伸长或缩短。

2、直杆轴向拉伸或压缩时横截面上的内力与应力内力：把拉伸时的轴力（轴力背向截面）为正，压缩时轴力（轴力指向截面）为负。

应力：平面假设（变形前原为平面的横截面，变形后仍保持为平面且仍垂直于轴线。

）规定：拉应力为正，压应力为负。

AF A dA F N A N =⇒==⎰σσσ 式中N F 为轴力，A 为横截面面积，σ为正应力。

3、直杆轴向拉伸或压缩时斜截面上的应力ασσα2cos = αστα2sin 2= 式中ασ和ατ分别为斜截面的正应力和切应力，σ为横截面的正应力，α为斜截面与横截面的夹角。

4、材料拉伸时的力学性能 应变：ll ∆=ε l ∆为伸长量，l 为原始长度。

（1）弹性阶段：应力σ与应变ε成正比，即εσE =。

其中E 为与材料有关的比例常数，为弹性模量。

直线部分的最高点a 所对应的应力p σ为比例极限。

b 点所对应的应力e σ为弹性极限。

（2）屈服阶段：通常把下屈服极限称为屈服极限或屈服点，用s σ表示。

其是衡量材料强度的重要指标。

（3）强化阶段：强化阶段中的最高点e 所对应的应力b σ是材料能承受的最大应力，称为强度极限。

其是衡量材料强度的另一重要指标。

（4）局部变形阶段：某一局部的横向尺寸急剧缩小，形成缩颈现象。

伸长率：%1001⨯-=ll l δ 塑性材料：%5>δ 脆性材料：%5<δ 断面收缩率：%1001⨯-=A A A ψ A 为原始横截面积，1A 为最小横截面积 5、材料压缩时的力学性能低碳钢压缩时的弹性模量E 和屈服极限s σ与拉伸时相同。

但是得不到强度极限。

铸铁的抗压强度极限比抗拉极限高5~4倍。

6、失效、安全因数和强度计算脆性材料断裂时的应力是强度极限b σ，塑性材料屈服时的应力是屈服极限s σ，这二者是构件失效时的极限应力。

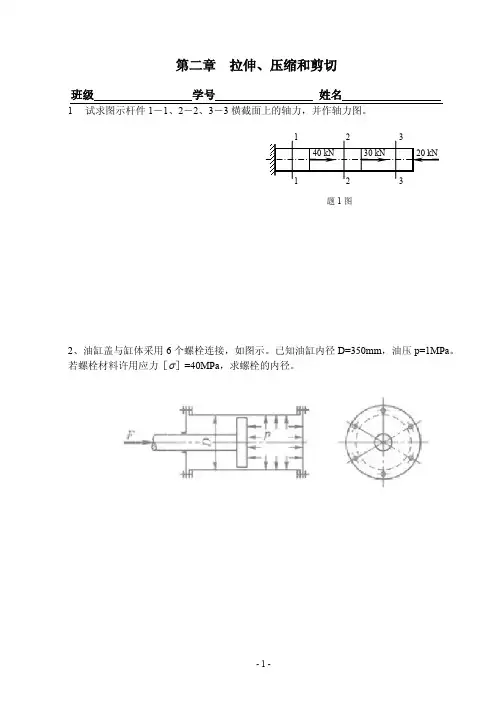
班级 学号 姓名1 试求图示杆件1－1、2－2、3－3横截面上的轴力，并作轴力图。

2、油缸盖与缸体采用6个螺栓连接，如图示。

已知油缸内径D=350mm ，油压p=1MPa 。

若螺栓材料许用应力［ ］=40MPa ，求螺栓的内径。

题1图140 kN 30 kN20 kN122 33班级 学号 姓名3 图示木制桁架受水平力P 作用。

已知P=80kN[][]MPa MPa 10,8==压拉σσ，试设计AB 、AD 两杆的横截面积。

4 图示结构，杆1、2的横截面均为圆形，直径分别为d 1=30mm , d 2=20mm 。

两杆材料相同，许用应力[σ]=160MPa ，在节点A 处受铅直力P=80kN 。

试校核结构的强度。

A B C D P60° 60° 30° 30°BC A P 12 30° 45°班级学号 姓名5、某铣床工作台进给油缸如图示，缸内油压p=2MPa ，油缸内径D=75mm ，活塞杆直径 d=18mm 。

已知活塞材料的许用应力［σ］=50MPa ，试校核活塞杆的强度。

6、简易吊车如图所示。

AB 为木杆，横截面积 21cm 100=A ，许用压应力[]MPa 71=σ。

BC 为钢杆，横截面积22cm 6=A ，许用拉应力[]MPa 1602=σ。

试求许可吊重F 。

F30°AB C木杆 钢杆第二章 拉伸、压缩和剪切班级 学号 姓名7、 图示拉杆沿斜截面m －m 由两部分胶合而成。

设在胶合面上许用拉应力[]MPa 100=σ，许用切应力[]MPa 50=τ，并设胶合面的强度控制杆件的拉力。

试问：为使杆件承受最大拉力F ，α角的值应为多少？若杆件横截面面积为4cm 2，并规定α≤60°，试确定许可载荷F 。

8、变截面杆如图所示。

已知：21cm 8=A ，22cm 4=A ， GPa 200=E 。

试求杆的总伸长l ∆。