材料力学答案-剪切的实用计算
- 格式:doc
- 大小:356.00 KB
- 文档页数:8



剪切与挤压的实用计算1.基本理论剪切是指沿着平面内条线上的应力沿剪切方向相对另一平面移位的力。
材料在受到剪切力作用时,会发生剪切变形并产生剪切应力。
剪切应力τ的计算公式为:τ=F/A其中,τ表示剪切应力,F表示受力,A表示受力面积。
材料的抗剪强度表示了材料在剪切载荷下破坏的抵抗能力,通常用剪切强度σs表示,剪切强度也可以通过横截面上的最大剪切应力来计算,即σs = τmax。
2.剪切计算方法在实际工程中,剪切常常涉及到材料的剪切强度计算、剪切连接件的设计以及剪切抗力的计算等。
(1)剪切强度计算根据材料的剪切性能参数,可以计算材料的抗剪强度。
一般来说,剪切强度与材料的抗拉强度有一定的关系。
对于金属材料来说,一般有以下公式用于计算剪切强度:σs=k·σu其中,σs表示材料的剪切强度,k表示剪切系数,一般取0.6~0.8,σu表示材料的抗拉强度。
(2)剪切连接件设计在机械设计中,常常需要设计剪切连接件,如销轴连接、键连接等。
设计剪切连接件时,需要根据剪切载荷和材料的强度参数来计算连接件的尺寸。
以销轴连接为例,假设在动力传动系统中,传递的扭矩为T,需设计一个销轴连接。
根据材料的抗剪强度和材料的弹性模量,可以计算出销轴的直径d。
d=[16·T/(π·τs)]^(1/3)其中,d表示销轴的直径,T表示扭矩,τs表示材料的抗剪强度。
(3)剪切抗力计算在工程结构设计中,剪切抗力的计算是非常重要的。
常见的剪切抗力计算方法有剪切弯曲理论、剪切流动理论等。
对于简支梁的剪切抗力计算来说,可以使用剪切弯曲理论。
根据弯矩与剪力之间的关系,可以得到梁上任意一点的剪切力V和弯矩M之间的关系:V = dM / dx其中,V表示剪切力,M表示弯矩,dM表示单位长度上的弯矩的变化,dx表示单位长度。
1.基本理论挤压是指沿轴线方向作用于材料上的静态或动态力。
当材料受到挤压力作用时,会发生长度方向的变形,并产生挤压应力。
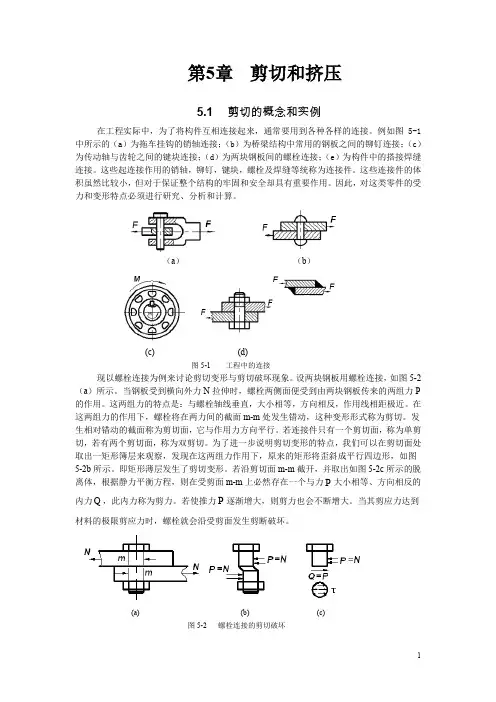
第5章剪切和挤压5.1 剪切的概念和实例在工程实际中,为了将构件互相连接起来,通常要用到各种各样的连接。
例如图5-1中所示的(a)为拖车挂钩的销轴连接;(b)为桥梁结构中常用的钢板之间的铆钉连接;(c)为传动轴与齿轮之间的键块连接;(d)为两块钢板间的螺栓连接;(e)为构件中的搭接焊缝连接。
这些起连接作用的销轴,铆钉,键块,螺栓及焊缝等统称为连接件。
这些连接件的体积虽然比较小,但对于保证整个结构的牢固和安全却具有重要作用。
因此,对这类零件的受力和变形特点必须进行研究、分析和计算。
(a)(b)(c) (d)图5-1 工程中的连接现以螺栓连接为例来讨论剪切变形与剪切破坏现象。
设两块钢板用螺栓连接,如图5-2(a)所示。
当钢板受到横向外力N拉伸时,螺栓两侧面便受到由两块钢板传来的两组力P 的作用。
这两组力的特点是:与螺栓轴线垂直,大小相等,方向相反,作用线相距极近。
在这两组力的作用下,螺栓将在两力间的截面m-m处发生错动,这种变形形式称为剪切。
发生相对错动的截面称为剪切面,它与作用力方向平行。
若连接件只有一个剪切面,称为单剪切,若有两个剪切面,称为双剪切。
为了进一步说明剪切变形的特点,我们可以在剪切面处取出一矩形簿层来观察,发现在这两组力作用下,原来的矩形将歪斜成平行四边形,如图5-2b所示。
即矩形薄层发生了剪切变形。
若沿剪切面m-m截开,并取出如图5-2c所示的脱离体,根据静力平衡方程,则在受剪面m-m上必然存在一个与力P大小相等、方向相反的内力Q,此内力称为剪力。
若使推力P逐渐增大,则剪力也会不断增大。
当其剪应力达到材料的极限剪应力时,螺栓就会沿受剪面发生剪断破坏。
(a) (b) (c)图5-2 螺栓连接的剪切破坏5.2剪切和挤压的实用计算5.2.1剪切的实用计算受剪切的连接件一般大多为短粗杆,且剪切变形均发生在某一局部,要从理论上计算它们的工作应力往往非常复杂,有时甚至是不可能的。
即使用精确理论进行分析,所得结果也会与实际情况有较大的出入。


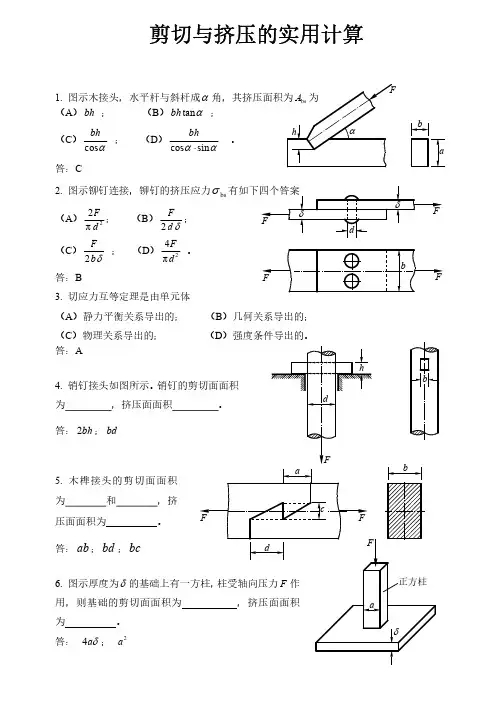
剪切与挤压的实用计算1.图示木接头,水平杆与斜杆成(A )bh ;(B )tan bh ;(C )cos bh;(D )cos sin bh。
答:C2.图示铆钉连接,铆钉的挤压应力bs(A )22π Fd ;(B )2Fd;(C )2Fb;(D )24πFd 。
答:B3.切应力互等定理是由单元体(A )静力平衡关系导出的;(B )几何关系导出的;4.5.6.7. 图示直径为d 的圆柱放在直径为3D d ,厚度为 的圆形基座上,地基对基座的支反力为均匀分布,圆柱承受轴向压力F ,则基座剪切面的剪力S F 。
答: 22S 2π 48π 49D dF F F D8. 拉杆及头部均为圆截面,已知40 mm D ,20 mm d ,15 mm h 。
材料的许用切应力[]100 MPa ,许用挤压应力bs []240 MPa ,试由拉杆头的强度确定许用拉力F 。
解:S π []94.3 kN F d h22bsbs π[]226 kN 4D d F取[]94.3 kN F 。
9. 图示在拉力F 的作用下的螺栓,已知螺栓的许用切应力[] 是拉伸许用应力的0.6倍。
试求螺栓直径d 和螺栓头高度h 的合理比值。
解:24[]πF d 因为,0.6[]πFd h所以在正应力和切应力都达到各自许用应力时,有241π0.6πFd F dh , 2.4d h 。
10. 图示键的长度30 mm l ,键许用切应力[]80 MPa ,许用挤压应力bs []200 MPa ,试求许可载荷][F 。
解:以手柄和半个键为隔离体, S 0, 204000O M F F取半个键为隔离体,bs S 20F F F由剪切:S []sFA ,720 N F由挤压:bs bs bs bs [][], 900N FF A取[]720N F 。



第5章剪切和挤压5.1 剪切的概念和实例在工程实际中,为了将构件互相连接起来,通常要用到各种各样的连接。
例如图5-1中所示的(a)为拖车挂钩的销轴连接;(b)为桥梁结构中常用的钢板之间的铆钉连接;(c)为传动轴与齿轮之间的键块连接;(d)为两块钢板间的螺栓连接;(e)为构件中的搭接焊缝连接。
这些起连接作用的销轴,铆钉,键块,螺栓及焊缝等统称为连接件。
这些连接件的体积虽然比较小,但对于保证整个结构的牢固和安全却具有重要作用。
因此,对这类零件的受力和变形特点必须进行研究、分析和计算。
(a)(b)(c) (d)图5-1 工程中的连接现以螺栓连接为例来讨论剪切变形与剪切破坏现象。
设两块钢板用螺栓连接,如图5-2(a)所示。
当钢板受到横向外力N拉伸时,螺栓两侧面便受到由两块钢板传来的两组力P 的作用。
这两组力的特点是:与螺栓轴线垂直,大小相等,方向相反,作用线相距极近。
在这两组力的作用下,螺栓将在两力间的截面m-m处发生错动,这种变形形式称为剪切。
发生相对错动的截面称为剪切面,它与作用力方向平行。
若连接件只有一个剪切面,称为单剪切,若有两个剪切面,称为双剪切。
为了进一步说明剪切变形的特点,我们可以在剪切面处取出一矩形簿层来观察,发现在这两组力作用下,原来的矩形将歪斜成平行四边形,如图5-2b所示。
即矩形薄层发生了剪切变形。
若沿剪切面m-m截开,并取出如图5-2c所示的脱离体,根据静力平衡方程,则在受剪面m-m上必然存在一个与力P大小相等、方向相反的内力Q,此内力称为剪力。
若使推力P逐渐增大,则剪力也会不断增大。
当其剪应力达到材料的极限剪应力时,螺栓就会沿受剪面发生剪断破坏。
(a) (b) (c)图5-2 螺栓连接的剪切破坏5.2剪切和挤压的实用计算5.2.1剪切的实用计算受剪切的连接件一般大多为短粗杆,且剪切变形均发生在某一局部,要从理论上计算它们的工作应力往往非常复杂,有时甚至是不可能的。
即使用精确理论进行分析,所得结果也会与实际情况有较大的出入。
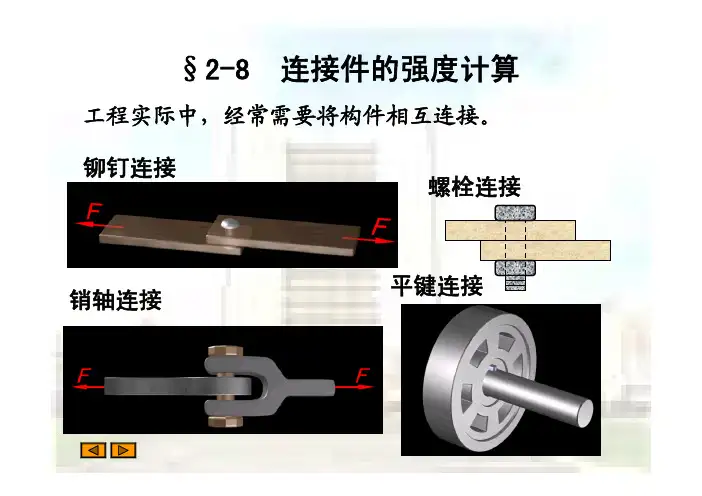
剪切和挤压实用计算剪切和挤压是材料力学中常见的载荷形式,广泛应用于工程实践中。
剪切是指在材料中施加垂直于表面的切力,而挤压是指在材料中施加平行于表面的压力。
在工程设计和材料选择过程中,必须对剪切和挤压的载荷进行合理的计算,以确保结构和材料的安全性和可靠性。
本文将介绍剪切和挤压的实用计算方法,并提供一些实际应用案例,以帮助读者更好地理解和应用这些计算方法。
一、剪切的实用计算1.剪切力的计算剪切力是指作用在材料上的垂直于断面的力,可通过以下公式进行计算:剪切力=剪切应力×断面积其中,剪切应力是材料上的剪切应力,可以通过以下公式进行计算:剪切应力=剪切力/断面积2.剪切应力的计算剪切应力是剪切力对应的应力,即单位面积上的剪切力。
对于不同的材料,剪切应力的计算方法略有不同。
对于均匀材料,可以使用以下公式计算剪切应力:剪切应力=剪切力/断面积对于层合材料,由于材料的不同层之间可能存在剪切位移,剪切应力的计算较为复杂。
通常使用剪切力与剪切位移之间的关系来计算剪切应力。
3.剪切应变的计算剪切应变是指材料在受到剪切应力作用时产生的变形。
剪切应变的计算可以使用以下公式:剪切应变=切变角/材料长度其中,切变角可以通过材料变形前后标记点的位移计算得到。
二、挤压的实用计算1.挤压压力的计算挤压压力是指作用在材料上的平行于表面的压力,可以通过以下公式进行计算:挤压压力=挤压应力×断面积其中,挤压应力是指单位面积上的挤压力,可以通过以下公式进行计算:挤压应力=挤压压力/断面积2.挤压应力的计算挤压应力是指挤压压力对应的应力,即单位面积上的挤压力。
对于不同的材料,挤压应力的计算方法略有不同。
对于均匀材料,可以使用以下公式计算挤压应力:挤压应力=挤压压力/断面积对于复杂的材料结构,可以将材料分解为多个小单元,分别计算其挤压应力,再根据应力平衡原理计算整个结构的挤压应力。
3.挤压应变的计算挤压应变是指材料在受到挤压应力作用时产生的变形。
习 题
3-1 夹剪的尺寸如图示,销子C 的直径d =0.5 cm ,作用力F=200 N ,在剪直径与用子直径相同的铜丝A 时,若a =2cm ,b =15cm .试求铜丝与销子横截面上的平均剪应力τ。
解:
QA F b F a ⨯=⨯ 2001515002QA Fb F N a ==⨯= 22444150076.390.510
QA
A F MPa d τππ-⨯===⨯⨯ ()QC F a b F a +=⨯
()200(215)17002
QC F a b F N a ++=
== MPa C 58.86105.01700442=⨯⨯⨯=-πτ 3-2 图示摇臂,试确定其轴销B 的直径d 。
已知用材料的许用应力[τj ]=100Mpa,
[σbs ]=240Mpa 。
解:
0=∑B M
cos450.6500.4F ⋅⨯=⨯
47.14F KN =
37.27B F KN =
[]24
2B F d πττ=≤ []3
262237.2710 1.541010010
B F d m πτπ-⨯⨯===⨯⨯⨯=15.4mm 验算挤压应力
[]32237.27102421.5410110B bs bs bs F MPa A σσ--⨯===≈⨯⨯⨯ 3-3 图示直径为 d 的拉杆,其端头的直径为D ,高度为h ,试建立 D 、h 与d 的合理比值(从强度考虑)。
已知:[σ]=120 MPa ,[τj ]=90 MPa ,[σbs ]=240 MPa .
解:
[]
310030.14-⨯==P P
d σπ []jy p d D σπ
π=-2244
310261.1-⨯=P D
[]
310717.12-⨯==P d P h τπ ∴67.1:22.1:1::=h D d 3-4 两根矩形截面木杆,用两块钢板
连接在一起,受轴向载荷P =45kN 作用。
已知截面宽度 b =25 cm ,沿材的顺纹方向,许用拉应力[σ]=6MPa ,许用挤压应力[σjy ]=10 MPa ,许用剪应力[τj ]=1MPa ,试确定接头的尺寸δ、l 和 h 。
解
[]τ≤⋅b
l P 2 []mm m b P l 9009.010
1025210452623==⨯⨯⨯⨯=⋅⋅=-τ []
jy b P σδ≤⋅2 []mm m b P jy 9009.010
101025210452623==⨯⨯⨯⨯⨯=≥σδ []σδ≤-b
h P )2(
[]mm m b p h 48048.0009.02106102510452623
==⨯+⨯⨯⨯⨯=+≥-δσ 3-5 货轮的传动轴和艉轴系利用轴端凸缘法兰上的12只螺栓相联接,螺栓直径d =75 mm ,螺栓中心圆的直径D=650 mm ,已知传递的扭矩M n =600 kN ·m ,螺栓和轴的材料均为35号钢,其许用应力[j τ]=80Mpa,[σjy ]=120MPa 、试校核螺栓的剪切和挤压强度。
解:
Mn D P =⨯2
12 ∴KN D M P n 85.15365
.066006=⨯== []τππτ<=⨯⨯⨯⨯==-MPa d P 8.3410
751085.15344623
2 []
jy jy jy MPa A P σσ<=⨯⨯⨯==-8.221090751085.15363 3-6 某拖轮的螺旋桨推进轴,其凸缘法兰承受总推力P=250KN ,凸缘最小宽度b=50mm ,材料为45号钢,许用剪应力[τj ]=22.5Mpa 。
试校合其剪切强度。
解
[]τππτ<=⨯⨯⨯==MPa rb P 979.305
.04.01025023
3-7 图示轴的直径d=80mm,键的尺寸b=24mm,h=14mm ,键的许用剪应力[τ
j ]=40Mpa ,
许用挤压应力[σjy ]=90Mpa 。
若通过键所传递的扭矩为3200N.m 。
试确定键的长度l 。
解:
n M d P =⨯2
KN d M P n 8010803200223
=⨯⨯==- []cm b P l 33.810
4010241030633
=⨯⨯⨯⨯=≥-τ
[]
cm h P l iy 7.1210901010103022633
=⨯⨯⨯⨯⨯=≥-σ 取mm l 127=
3-8 销钉式安全联轴器如图所示.允许传递扭矩M n =300N.m 。
销钉材料的剪切强度极限τb =360 MPa ,轴的直径D =30mm 。
试确定销订的直径d 。
解: KN D M Q n 1010
303003=⨯==- 24d Q b πτ= mm d 95.510
361010463
=⨯⨯⨯⨯=π 3-9 冲床的最大冲击力为400 kN ,冲头材料的许用应力[σ]=440MPa ,被冲钢板的剪切强度极限b τ=360 MPa .求在最大冲力作用下所能冲剪的圆孔的最小直径d 和的最大厚度t 。
解: []σπ≤24d
P []cm P
d 4.310440104004443
=⨯⨯⨯⨯=≥πσπ b td
P τπ≥ cm d P
t b 04.1104.31036010400263
=⨯⨯⨯⨯=≤-πτ 3-10 以楔C 把钩杆AB 固定联接于平板D 的孔中。
试求楔的尺寸:宽度δ,高度h 以
及钩杆的尾长x 。
设挤压许用应力[σjy ]=320MPa ,剪切许用应力[τj ]=100MPa ,P 力可由钩杆中的抗拉许用应力[σ]=160MPa 来求得。
解
[][]⎥⎦⎤⎢⎣⎡⨯-⨯⨯⨯⨯=⎥⎦⎤⎢⎣⎡⨯-⋅=⋅=--δπδπσσ22262104)104(4101604d d A P
δ6
210160104201061
--⨯⨯⨯-= 解之得: KN P 134=
mm m 47.1001047.0==δ 取mm 5.10=δ
[]mm P h 8.6310
100105.102134000105.102633=⨯⨯⨯⨯=⨯⨯≥--τ []mm d P
x 75.161040101002134000236=⨯⨯⨯⨯=≥
-τ 3-11 厚度为t=20mm 的钢板,上下用两块广度均为 t 1=10mm 的盖板和直径d =28 mm 的铆钉联接,每边铆钉数n =3,如图示,若钢的许用应力:[τj ]=100MPa ,[σjy ]=280MPa ,
[σ]=100Mpa 。
试求这个接头所能承受的许可拉力多少?
解: 柳钉:[]KN d P 6.318100264643222=⨯⨯=⨯=πτπ 挤压:[]
KN at P jy 8.436102801020102633433=⨯⨯⨯⨯⨯⨯==--σ
缀板: []KN d b t P 2.2461026421013020101604262662=⎪⎭
⎫ ⎝⎛⨯⨯⨯-⨯⨯⨯=⎥⎦⎤⎢⎣⎡⨯-⨯=--ππσ∴KN P 2.246=
将d=28mm 改为26mm ,[σ]改为160MPa 最后答案即为249.6KN.
正确答案是:
盖板:P=2*160*10*(130-26*2)=249.6
3-12 图示节点板用 4只直径为 d =17 mm 的铆钉固定在立柱上,已知节点板承受载荷P=20kN ,试求各铆钉内的剪应力。
解:
KN p Q y 54
204=== 2)40120(9021⨯⨯+⨯=⨯X X Q Q P
3401202
1
==X X Q Q
KN Q X 75.61= KN P Q X 25.245.02== KN Q Q Q X Y 8475.65221212=+=+= KN Q Q Q X Y 48.525.25222222=+=+=
MPa d Q 07.37010174108446
2321
1=⨯⨯⨯==-π
π
τ MPa d Q 14.24101741048.546
23
22
2=⨯⨯⨯==-π
π
τ。