【KS5U首发】河北省衡水中学11-12学年高二下学期一调考试(数学理)

河北省衡水中学2008—2009学年度第二学期一调考试高二年级数学试卷(理科)本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分。

第Ⅰ卷共2页，第Ⅱ卷共4页。

共150分。

考试时间120分钟。

第Ⅰ卷（选择题共60分）一、选择题（每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1.两位到北京旅游的外国游客要与2008奥运会的吉祥物福娃（5个）合影留念，要求排成一排且两位游客不站在两端，则不同的排法共有（）A.1440B.960C.720D.24002．五名学生和五名老师站成一排照相，五名老师不能相邻的排法有（）A.55552AA B.5655AA C.25655AA D.5555AA3．袋中装有4个红球和3个黄球，从中任取4个球，则既有红球又有黄球的不同的取法有（）A. 34种B. 35种C. 120种D. 140种4.关于直线m、n与平面α，β，有下列四个命题：①若m//α，n//β且α//β，则m//n；②若m⊥α，n⊥β且α⊥β，则m⊥n；③若m⊥α，n//β且α//β,则m⊥n；④若m//α，n⊥β且α⊥β，则m//n；其中真命题的序号是（）A.①②B.③④C.①④D.②③5.如图所示，在某试验区，用4根垂直于地面的立柱支撑一个平行四边形的太阳能电池板，可测得其中三根立柱AA1、BB1、CC1的长度分别为10m、15m、30m，则立柱DD1的长度是（）A.30mB. 20mC. 25mD.15m6.由1,2,3,4这四个数字组成的首位数字是1，且恰有三个相同数字的四位数有（）A.9个 B .12个 C.15个 D.18个7.正方形ABCD 沿对角线BD 折成直二面角后不会成立的结论是（ ） A.AC ⊥BD B.△ADC 为等边三角形 C.AB 、CD 所成角为060 D.AB 与平面BCD 所成角为0608..若直线)(1R k kx y ∈+=与焦点在x 轴上的椭圆17222=+a y x )0(>a 恒有公共点，则实数a的取值范围是（ ）A.10≤<aB.70<<a C. 71<≤a D. 71≤<a9.已知F 1、F 2分别是双曲线12222=-by a x （0>a ，0>b ）的左、右焦点，过F 1作垂直于x 轴的直线交双曲线于A 、B 两点，若△ABF 2为锐角三角形，则双曲线离心率的取值范围是（ ）A.(1,21+)B. (21+,∞+)C. (21-,21+)D.(2,21+)10.用0，1，2，3，4，5可以组成没有重复数字并且比20000大的五位偶数共有（ ） A. 288个 B144.个 C. 240个 D.126个 11．在正三棱锥S-ABC 中，M 、N 分别是棱SC 、BC 的中点，且MN ⊥AM ，若侧棱SA=32,则S 到平面ABC 的距离为( )A. 32B. 3 C 2 D.312.如果一个平面与一个正方体的十二条棱所在直线都成相等的角θ，那么sin θ的值为( ) A.22 B.33 C.55D.不确定 二、填空题（每题5分，共20分）13.与双曲线1242522=-y x 有公共焦点，准线与中心距离为8的椭圆方程是________________ 14.某银行储蓄卡的密码是一个4位数码，某人采用千位、百位上的数字之积作为十位、个位上的数字（如2816）的方法设计密码，当积为一位数时，十位上数字选0，千位、百位上都能取0.这样设计出来的密码共有_______个。

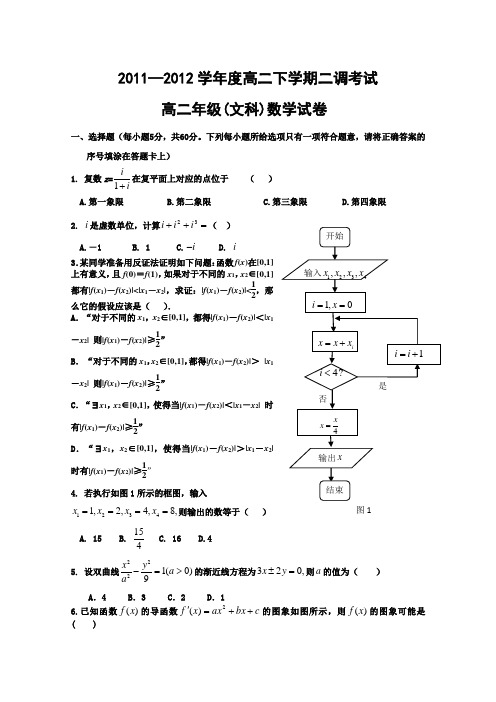
2011—2012学年度高二下学期二调考试高二年级(文科)数学试卷一、选择题（每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上） 1. 复数z =1ii+在复平面上对应的点位于 （ ） A.第一象限B.第二象限C.第三象限D.第四象限2. i 是虚数单位，计算=++32i i i （ ）A.－1B. 1C.i -D. i 3．某同学准备用反证法证明如下问题：函数f (x )在[0,1]上有意义，且f (0)＝f (1)，如果对于不同的x 1，x 2∈[0,1]都有|f (x 1)－f (x 2)|<|x 1－x 2|，求证：|f (x 1)－f (x 2)|<12，那么它的假设应该是（ ）．A ．“对于不同的x 1，x 2∈[0,1]，都得|f (x 1)－f (x 2)|＜|x 1－x 2| 则|f (x 1)－f (x 2)|≥12”B ． “对于不同的x 1，x 2∈[0,1]，都得|f (x 1)－f (x 2)|＞ |x 1－x 2| 则|f (x 1)－f (x 2)|≥12”C ．“∃x 1，x 2∈[0,1]，使得当|f (x 1)－f (x 2)|＜|x 1－x 2| 时有|f (x 1)－f (x 2)|≥12”D ．“∃x 1，x 2∈[0,1]，使得当|f (x 1)－f (x 2)|＞|x 1－x 2|时有|f (x 1)－f (x 2)|≥12”4. 若执行如图1所示的框图，输入12341,2,4,8,x x x x ====则输出的数等于（ ）A. 15B.415C. 16D.4 5. 设双曲线2221(0)9x y a a -=>的渐近线方程为320,x y ±=则a 的值为（ ） A ．4 B ．3 C ．2 D ．16.已知函数)(x f 的导函数c bx ax x f ++='2)(的图象如图所示，则)(x f 的图象可能是( )图17 . 复数=+---+iii i 32233223（ ） A 、0B 、2C 、i 2-D 、i 28. 如下图为一串白黑相间排列的珠子，按这种规律往下排起来，那么第36颗珠子应是什么颜色的（ ）A ．白色B ．黑色C ．白色可能性大D ．黑色可能性大 9. 函数a ax x y +-=23在)1,0(内有极小值，则实数a 的取值范围为（ ） A.(0,3) B. )3,(-∞ C. ),0(+∞ D. )23,0(10. 将两个顶点在抛物线()022>=p px y 上，另一个顶点是此抛物线焦点的正三角形的个数记为n ，则（ ）A. 0=nB. 1=nC. 2=nD. 3≥n11. 对实数a 和b ，定义运算“⊗”：⎩⎨⎧>≤=⊗b a b ba ab a ,,设函数R x x x x f ∈+⊗=),2()(2若函数c x f y -=)(的图像与x 轴恰有三个公共点，则实数c 的取值范围是（ ）A ．[)0,1-B ．)1,0(C ．),0(+∞D ．[)+∞⋃-,1)0,1(12. 若执行如右图所示的框图，1x ，2x ，3x 为某次考试三个评阅人对同一道题的独立评分，p 为该题的最终得分，当16x =，29x =，8.5p =时，3x 等于（ ）A. 11B.10C. 8D. 7二、填空题（每题5分，共20分。

.下学期高二年级一调考试理科数学试卷第Ⅰ卷一、选择题（本大题共 12 个小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只有一项是符合题目要求的）1、已知 i 是虚数单位， m 和 n 都是实数，且 m(1i )7 ni ，则mni （）m niA ．-1B ． 1C ．-ID ． i2、复数 Z 点 Z 对应， Z 1, Z 2 为两个给定的复数， Z 1Z 2，则 Z Z 1Z Z 2 决定的 Z的轨迹是（）A ．过 Z 1, Z 2 的直线B．线段 Z 1, Z 2 的中垂线C ．双曲线的一支D ．以 Z 1, Z 2 为端点的圆a, b 的方向向量分别是 ur uur3、设两个不同的直线 e 1 ,e 2 ，平面ur uur ur rur uure 1 // e 2 e 1 // e 2 b //e 1 // na //b ；③ b①ur r；② uur re 1 // ne 2 // nur uure 1 e 2r的法向量是 n ，则下列推理ur uure 1 // e 2b ；b //；④urre 1 // n其中正确的命题序号是（ ）A ．①②③B ．②③④C ．①③④D ．①②④4、若 ( ax2b)4 的展开式中 x 3 的系数为 20，则 a 2 b 2 的最小值为（）xA ． 1 B．2C ．3D ．45、 2(2cos 2xtan x)dx （）2 2．2 B ．2C．D ．2A226、已知 x 表示不超过实数x 的最大整数 ( x R) ，如： 1.3 2, 0.8 0, 3.43，定义 xx x ，求 {1 } { 2} { 3 } L{ 2014}（）2014 2014 20142014A ． 2013 B． 2013C．1007 D． 201427、若不等式 ( 1)n a 2( 1)n 1 对于任意正整数 n 恒成立， 则实数 a 的取值范围是 （）n.33A．[ 2, ] B ．( 2, ] C ．[ 3,2]D ．( 3,1)228、将n2个正整数1,2,3,L n2填入 n n 方格中，使其每行、每列、每条对角线上的数的和相等，这个正方形叫做n 阶幻方，记f n 为n阶幻方对角线的和，如图就是一个 3 阶幻方，可知 f 315 ，则 f5（）A． 63 B ．64C． 65D． 669、某班班会准备从含有甲乙丙的7 名学生中选取 4 人发言，要求甲乙至少有一人参加，若甲乙同时参加市，丙不能参加，且甲乙两人的发言顺序不能相邻，那么不同的发言顺序有（）A．484 种B．552种C．560种D．612种10、某次联欢会要安排 3 个歌舞类节目、 2 个小雷节目和 1 个相声类急忙的演出顺序，则同类节目不相邻的排法种数是（）A．72B．120C．144 D．16811、用 a 代表红球， b 代表篮球， c 代表黑球，由加法原理及乘法原理，从 1 个红球和 1 个篮球中取出若干个求的所有取法可由(1 a)(1 b) 的展开式1 a b ab 表示出来，如：“1”表示一个球都不取，“ a”表示取出一个红球，而“ ab”则表示把红球和篮球都取出来，依次类推，下列各式中，其展开式可用来表示从 5 个无区别的红球， 5 个无区别的篮球， 5 个有区别的黑球中取出若干个球，且所有的篮球都取出或都不取出的所有取法的是（）A．(1 a a2a3a4a5 )(1b5 )(1c)5B．(1a5 )(1b b2b3b4b5 )(1c)5C．(1a5 )(1b b2b3b4b5 )(1c5 )D．(1a5 )(1b)5 (1c c2c3c4c5 )12、已知函数y f x 对于任意的 x (, ) 满足 f x cosx f x sin x 0 （其中22f x 是函数 f x的导函数），则下列不等式不成立的是（）A．C．2 f ( ) f ()34f (0) 2 f ()4B． 2 f () f ( )34D． f (0) 2 f ()3第Ⅱ卷二、填空题：本大题共/4 小题，每小题 5 分，共 20 分，把答案填在答题卷的横线上。

高二年级理科数学试卷第I 卷 选择题 （共60分）选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.复数z 满足()52)(=--i i z ，则复数z 在复平面内对应的点位于 （ ） A.第一象限 B.第二象限C.第三象限D.第四象限2．“a = 1”是“复数21(1)a a i -++（a R ∈，i 为虚数单位）是纯虚数”的（ ）A 充分不必要B 必要不充分C 充要条件D 既不充分也不必要3.在证明f(x)＝2x ＋1为增函数的过程中，有下列四个命题：①增函数的定义是大前提；②增函数的定义是小前提；③函数f(x)＝2x ＋1满足增函数的定义是小前提；④函数f(x)＝2x ＋1满足增函数的定义是大前提．其中正确的命题是 ( )． A ．①② B ．②④ C ．①③ D ．②③ 4.设a ，b ，c ∈(－∞，0)，则a ＋1b ，b ＋1c ，c ＋1a ( )A ．都不大于－2B ．都不小于－2C ．至少有一个不小于－2D ．至少有一个不大于－25.我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中，有5架舰载机准备着舰，如果甲、乙两机必须相邻着舰，而丙、丁两机不能相邻着舰，那么不同的着舰方法有（ ） A.12 B.18 C.24 D.486, 已知函数f(x)＝x3－px2－qx 的图象与x 轴相切于点(1,0)，则f(x)的极值情况为( ) A ．极大值427，极小值0 B ．极大值0，极小值427C ．极大值0，极小值－427D ．极大值－427，极小值07．已知抛物线y2＝4x 的准线过双曲线x2a2－y2b2＝1(a>0，b>0)的左顶点，且此双曲线的一条渐近线方程为y ＝2x ，则双曲线的焦距等于 ( )． A. 5 B ．2 5 C. 3 D ．2 38．已知空间四面体D ABC -的每条边都等于1，点,E F 分别是,AB AD 的中点，则FE DC ⋅等于 （ ）A ．14B ．14-C ．3D ．3-9．函数()1,10cos ,02x x f x x x π+-≤<⎧⎪=⎨≤≤⎪⎩的图象与x 轴所围成的封闭图形的面积为（ ） A.32 B.1 C.2 D.1210．已知双曲线的方程为)0,0(12222>>=-b a b y a x ，过左焦点1F 作斜率为33的直线交双曲线的右支于点P ，且y 轴平分线段P F 1,则双曲线的离心率为（ ） A ．3 B ．51+ C ．2 D ．23+11．把3盆不同的兰花和4盆不同的玫瑰花摆放在右图图案中的1,2,3,4,5,6,7所示的位置上，其中三盆兰花不能放在一条直线上，则不同的摆放方法为( )A ．2680种B ．4320种C ．4920种D ．5140种12．已知函数1()ln ln f x x x =+，则下列结论中正确的是（ ）A ．若1212,()x x x x <是()f x 的极值点，则()f x 在区间12(,)x x 内是增函数 B ．若1212,()x x x x <是()f x 的极值点，则()f x 在区间12(,)x x 内是减函数C ．0,x ∀>且1x ≠ ，()2f x ≥D ．00,x ∃> ()f x 在0(,)x +∞是增函数第Ⅱ卷 非选择题 （共90分）二、填空题 （本大题共4个小题，每小题5分，共20分）13. 用数学归纳法证明1＋12＋13＋…＋12n －1<n(n ∈N ，且n>1)，第一步要证的不等式是__________________________________________．14.已知函数f(x)＝⎩⎪⎨⎪⎧log2x x>0，3x x≤0且关于x 的方程f(x)＋x －a ＝0有且只有一个实根，则实数a 的取值范围是________．15. 学校资料室有相同的物理书3本，历史书2本，数学书4本，分别借给四个理科学生和三个文科学生，每人限借与本学科相关的书一本，求共有 种不同的借法。

2011—2012学年度高二下学期三调考试高二年级(理科)数学试卷一、选择题（每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1．如果函数24)(x x x f -=，那么 ()f i '=( ) （i 是虚数单位）A ．－2iB ．2iC ．6iD ．－6i2. 若一个三角形能分割为两个与自己相似的三角形，那么这个三角形一定是（ ）A.锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定 3. 函数()()()221f x x x =-+在区间[]0,2上的值域为（ ）A. [－2，0 ]B. [－4，1]C. [－4，0 ]D. [－2， 9] 4. 下列等于1的积分是（ ）A ．dx x ⎰10 B ．dx x ⎰+10)1( C ．dx ⎰101 D ．dx ⎰10215. 如图，⊙O 的直径AB =6 cm ，P 是AB 延长线上的一点，过P 点作⊙O 的切线，切点为C ，连接AC ， 若CPA ∠=30°，PB 的长为（ ）cm.A． B． C ．4 D ．36．家电下乡政策是应对金融危机，积极扩大内需的重要举措．我市某家电制造集团为尽快实现家电下乡提出四种运输方案，据预测，这四种方案均能在规定的时间T 内完成预期运输任务Q 0，各种方案的运输总量Q 与时间t 的函数关系如下图所示，在这四种方案中，运输效率(单位时间的运输量)逐步提高的是()7．将()y f x =的图象的横坐标伸长为原来的3倍，纵坐标缩短为原来的13，则所得函数 的解析式为（ ）A ．3(3)y f x =B ．11()33y f x =C ．1(3)3y f x =D ．13()3y f x = 8．如图所示, 圆的内接ABC ∆的∠C 的平分线CD 延长后交圆于点E , 连接BE , 已知5,7,3===BC CE BD , 则线段=BE ( )A ．157 B ．521C ．353D ．4 9. 用数学归纳法证明：1+21+31+)1,(,121>∈<-+*n N n n n 时，在第二步证明从n=k 到n=k+1成立时，左边增加的项数是（ ）A.k 2B.12-kC.12-kD.12+k 10．在极坐标系中，圆2cos ρθ=与方程π4θ=（0ρ>）所表示的图形的交点的极坐标是 ( )．A. ()1,1B. π1,4⎛⎫ ⎪⎝⎭C. π4⎫⎪⎭D. π2⎫⎪⎭ 11. AB 是圆O 的直径，EF 切圆O 于C ，AD ⊥EF 于D ，AD ＝2，AB ＝6，则AC 长为( )．A. B ．3 C． D ．212．函数f(x )＝sin x ＋2x ()3f π'，()f x '为f(x )的导函数，令a ＝－ 12，b ＝log 32，则下列关系正确的是( )A ．f(a )>f(b )B ．f(a )<f(b )C ．f(a )＝f(b )D ．f(|a |)<f(b )第Ⅱ卷（共90分）二、填空题（本大题共4小题，每题5分，共20分）13．若m R ∈，复数(2m 2-3m-2)+(m 2-3m+2)i 表示纯虚数的充要条件是 . 14．定积分dx x ⎰--2224=___________．15．把极坐标系中的方程2)3cos(=-πθρ化为直角坐标形式下的方程为 . 16．如右图，圆 O 的割线 PBA 过圆心 O ， 弦 CD 交 PA 于点F ，且△COF ∽△PDF ，ACOF BD PPB = OA = 2，则PF = .三、解答题（共70分。

河北省衡水中学高二下学期一调试题（数学理）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分，共150分。

考试时间1。

第Ⅰ卷（选择题 共60分）一、选择题（每小题5分，共60分.下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1. 袋中有5个黑球和6个白球，从中任取2个，以下每对事件是对立事件的是 A.恰有一个白球和恰有2个黑球； B.至少有1个黑球和全是黑球； C.至少有1个白球和至少有1个黑球； D.至少有1个黑球和全是白球2.给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行； ②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直； ③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中真命题的个数是 （ ） A ．1个 B ．2个 C ．3个 D ．4个3.设椭圆12622=+y x 和双曲线1322=-y x 的公共焦点为21,F F ，P 为两曲线的一个交点，则21cos PF F ∠的值等于（ ）A ．41B ． 91C ．31D ． 534. n∈N 且n<55，则乘积（55-n ）（56-n ）……（69-n ）等于（ ） A 、nnA --5569B 、1569nA - C 、1555nA - D 、1469nA -5.某公共汽车站上有5名乘客，沿途有10个车站，乘客下车的可能方式有 （ ） A.510 种 B.105 种 C.50 种 D.A510 种6.将甲、乙、丙、丁四名学生分到三个不同的班，每个班至少分到一名学生，则不同分法的种数为 （ ）.18A.24B.30C.36D7．底面边长与侧棱长均为a的正三棱柱ABC—A1B1C1中，已知M为A1B1的中点，则M到BC的距离是（）A.a215B.a419C.a25D.a278椭圆)0(12222≠=+abbyax的离心率为23，有一个焦点与抛物线xy342=的焦点重合，则 b 的值为 ( )A．3 B．3 C．2 D．19. 用0，1，2，3，4组成没有重复数字的全部五位数中，若按从小到大的顺序排列，则数字12340应是第（）个数.A.6B.9C.10D.810.在二项式251()xx-的展开式中，含4x的项的系数是 ( )A．10- B．10C．5- D．511.奥运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中小张和小赵只能从事前两项工作，其余三人均能从事这四项工作，则不同的选派方案共有A. 36种B. 12种C. 18种D. 48种12.已知两个集合{}10987654321,,,,,,,,,aaaaaaaaaaA=，{}54321,,,,bbbbbB=，若从A到B的映射f使得B中的每个元素都有原象，且)()()()(10321afafafaf≤≤≤≤，则这样的映射共有多少个（）A.126B.210C.252D.第Ⅱ卷（非选择题共90分）二、填空题（每题5分，共把答案填在答题纸的横线上）13.设地球O的半径为R，P和Q是地球上两地，P在北纬450东经Q在北纬450东经1100，则P，Q两地的球面距离为_______.14. 某校要求每位学生从8门课程中选修5门，其中甲、乙两门课程至少选修一门，则不同的选课方案有 种．15．盒中装着标有数字1，2，3，4的卡片各2张，从盒中任取3张，每张卡片被抽出的可能性相等，则抽出的3张卡片上最大的数字是4的概率为__________.16.设21,F F 为椭圆1422=+y x 的两焦点，点P 在椭圆上，当21PF F ∆的面积为1时，21PF ∙ 的值为________.三、解答题（本大题共6个小题，共７０分，解答应写出文字说明、证明过程或演算步骤）。

2011—2012学年度高二上学期一调考试高二年级(理科)数学试卷一、选择题（每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1. 过点P(-3,1),Q(0,m)的直线的倾斜角α的范围为[3π，32π]，则m 值的范围为（ ）A.m ≥2B.-24≤≤mC.m 2-≤或m ≥4D.m ≤0或m ≥2.2.如果点（5，b ）在两条平行线6x-8y+1=0,3x-4y+5=0之间,则b 应取的整数值为（ ）A.-4B.4.C.-5D.5.3．若过点P(-2,1)作圆222)1()3(r y x =++-的切线有且只有一条，则圆的半径r 为（ ）A.29B. 29C. 小于29D. 大于29.4. 过圆x 2+y 2-2x+4y- 4=0内一点M （3，0）作直线 ，使它被该圆截得的线段最短，则直线 的方程是（ ）A ．x+y-3=0B ．x-y-3=0C ．x+4y-3=0D ．x-4y-3=05．函数3()sin 1()f x x x x R =++∈，若3)(=a f ,则()f a -的值为（ ） A.3 B.0 C.-1 D.-26.圆01222=++-+y ax y x 关于直线01=--y x 对称的圆的方程为122=+y x , 则实数a 的值为（ ）A ．0B ．6C ． ±2D ．2 7. 已知p ：,0)3(:,1|32|<-<-x x q x 则p 是q 的（ ） A ．必要不充分条件 B ． 充分不必要条件 C ．充要条件 D ．既不充分也不必要条件8. 直线)0(>+=n n my x 经过点)34,4(A ，若可行域⎪⎩⎪⎨⎧≥≥-+≤003y y x n my x 围成的三角形的外接圆的直径为3314，则实数n 的值是（ ） A. 3或5 B.4或5 C. 3或6 D.3或49. 已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2， 则两圆的圆心距等于（ ） A ．1B ．2C ．3D ．210. 已知等比数列{n a }中，各项都是正数，且1a ，321,22a a 成等差数列，则=++6587a a a a （ ）A.112-C. 3+D.3-11. 若关于x 的方程3)2(42+-=-x k x 有两个不等实数根，则实数k 的范围是 （ ）A. 53(,]124 B.5(,)12+∞ C.13(,]24 D.5(0,]1212. 若直线1x ya b+=通过点(cos sin )M αα，，则（ ）A ．221a b +≤B ．221a b +≥ C ．22111a b+≥D ．22111a b+≤ 二、填空题（每题5分，共20分。

一、教学目标? 利用地图说明全球海陆分布的特点,记住海陆面积比例;运用地图判别岛屿、大陆、大洲、半岛及大洋、海和海峡;运用地图说明七大洲、四大洋的名称、位置、轮廓和分布特点。

二、教学重点? 记住海陆面积比例;运用地图说明七大洲、四大洋的名称和位置。

三、教学难点 众多概念的理解、众多地名的记忆 四、教具准备? 地球仪、 “世界地形图”、“世界海陆分布图”及以它为底图的各大洲轮廓剪成的图片,并为每张学生桌上准备一个小地球仪。

、教学方法 读图启发式、讲述法、讲解法、讨论法 ?、教学过程? 导入新课? 1.世界上第一位乘宇宙飞船进入太空的宇航员是谁? 2.他为什么说地球起错了名字,不应叫“地球”,而应改名叫“水球”?把学生的注意力集中起来,激发学生学习地理的兴趣,很自然地导入新课。

观察地球仪和“世界海陆分布图” 1.海陆面积哪个较大? 2.比例大概是多少??让学生进一步加深“水球”的印象,为后面的讨论作铺垫讨论? 1.加加林说得有没有道理? 2.是否应该把“地球”改为“水球”?2.地球上海陆分布是否均匀??.联系东西半球、南北半球划分的“旧知”,看哪个半球陆地大些?? .通过地球仪演示归纳:任一半球,海洋? 陆地? 通过观察,分析海陆分布大势,培养学生的观察能力和分析能力? 读图? 1.指导学生读图2.5“大陆、半岛、岛屿与海洋”,讲解岛屿、大陆、大洲、半岛及大洋、海和海峡的概念,并理解它们之间的关系,例如:大洲=大陆+附近岛屿? 2.出示“世界地形图”,让学生找出其中的岛屿、大陆、大洲、半岛及大洋、海和海峡图2.5(景观图)。

生动直观,可使学生通过观察、比较、概括得到准确的概念;通过想象,又可把概念迁移到地形图(平面图)上。

观察地球仪和“世界地形图”? 1.上指出七大洲的位置2.分别找出东西半球、南北半球上的大洲;? 3.读“世界地形图”,找出各大洲的分界? 记忆、训练? 1.观察七大洲面积的大小;? 2.投影七大洲面积数据,看谁能又快又好地记住大小顺序;? 3.老师示例谐音记忆:亚非美(北美)男(南美)是南极欧阳(大洋洲)? 适时进行学法指导,让学生总结适合自己的记忆方法? 观察地球仪和“世界地形图”? 1.七大洲各被哪些大洋包围?? 2.分别在“世界地形图”、地球仪上指出四大洋位置;? 3.比较四大洋面积的大小。

2011-2012 学年度高二上学期期末考试高二年级数学试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷( 非选择题 ) 两部分，共 150分。

考试时间120分钟。

第Ⅰ卷（选择题共 60分）一、选择题（每题5分，共 60分 . 以下每题所给选项只有一项切合题意，请将正确答案的序号填涂在答题卡上）1.已知变量 a， b 已被赋值，要互换a、 b 的值，采纳的算法是（）A ． a=b, b=a B． a=c, b=a, c=b C．a=c, b=a, c=a D． c=a, a=b, b=c2.“ ab 0 ”是方程“ax2by2 c ”表示双曲线的()A. 必需不充足条件B.充足不用要条件C. 充要条件D.既不充足也不用要条件3.甲、乙两人独立地解同一问题，甲解决这个问题的概率是p1，乙解决这个问题的概率是 p ，那么恰巧有 1 人解决这个问题的概率是（）2A．p1p2B．p1(1 p2) p2(1 p1)C．1 p1p2D．1(1 p1 )(1p2 )4.假如随机变量: N( , 2),且E3, D1,那么 P(24) 等于（）（此中 N(μ , σ2) 在 ( μ－σ , μ＋σ ) 内的取值概率为 0.683 ；在 ( μ－ 2σ , μ＋ 2σ) 内的取值概率为0.954 ；在 ( μ－ 3σ , μ＋ 3σ ) 内的取值概率为 0.997 ）A． 0.5B． 0.683C． 0.954D．0.9975.若 (2 x 3) 4a0a1 x a2 x2a3 x3 a4 x4，则 (a0 a2a4 )2(a1a3 )2的值为（）A. 1 B ．1 C ．0 D ．26.高二年级举行一次演讲赛共有10 位同学参赛，此中一班有 3 位，二班有 2 位，其余班有 5 位，若采纳抽签的方式确立他们的演讲次序，则一班有 3 位同学恰巧被排在一起（指演讲序号相连），而二班的 2 位同学没有被排在一同的概率为：（）A.1B.1 C.1 D.11020401207. 10 件产品，此中 3 件是次品，任取两件， 若表示取到次品的个数， 则 E 等于（ ）A ． 3B ．8C ．14 51515D ． 18.从 6 个正方形拼成的 12 个极点 ( 如图 ) 中任取 3 个极点作为一组，此中能够组成三角形的组数为A ． 208B ．204 C()．200D． 1969. 20 名学生，随意分红甲、乙两组，每组10 人，此中 2 名学生干部恰巧被分在不一样组内的概率是（）A ． C 21C 189B ． 2C 21C 188C ． 2C 21C 198D ． C 21C 188C 2010C 2010C 2010C 201010. 空间 6 个点，随意四点都不共面，过此中随意两点均有一条直线，则成为异面直线的对数为（）A ． 15B ． 30C ． 45D ．6011. 一块各面均涂有油漆的正方体被锯成1000 个大小同样的小正方体，若将这些小正方体均匀地搅混在一同，则随意拿出一个正方体其两面涂有油漆的概率是（ ）A ．1B．1C ．3D． 1212102512512. 椭圆 x2y 2 1(a b) 的右焦点 F ，其右准线与 x 轴的交点为 A ，在椭圆上存在a 2b 2点 P 知足线段 AP 的垂直均分线过点 F ，则椭圆离心率的取值范围是（）A.0,2B.0,1C. 2 1,1D.1,1222第Ⅱ卷（非选择题 共 90分）二、填空题（每题5分，共 20分 . 把答案填在答题纸的横线上）．．．．．．．．13.设 a, b (0,1) ，则对于 x 的方程 x 22ax b 20 在 (, ) 上有两个不一样的零点的概率为 ______________.14. 已知数据 x 1, x 2 ,, x n 的均匀数 x 5 ，方差 S 2 4 则数据 3x 1 7,3x 2 7, ,3x n 7的准差。

2012—2013学年度第一学期第一次调研考试高二年级数学（理科）试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷((非选择题非选择题))两部分，共两部分，共150150150分。

考试时间分。

考试时间分。

考试时间120120120分分钟。

第Ⅰ卷（选择题共60分）注意事项：1.1.答卷Ⅰ前，考生将自己的姓名、准考证号、考试科目涂写在答题卡上。

答卷Ⅰ前，考生将自己的姓名、准考证号、考试科目涂写在答题卡上。

2.2.答卷Ⅰ时，答卷Ⅰ时，每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

一、选择题（每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1.若011<<ba ，则下列不等式不正确．．．的是（）A.ab b a <+B.2>+ba ab C.2b ab < D.22b a >2. 数列{n a }的通项公式是n a ＝122+n n(n Î*N )，那么n a 与1+n a 的大小关系是（）A.n a ＜1+n aB.n a ＞1+n aC.n a ＝1+n aD.不能确定3．已知等差数列{}na 中，n S 是它的前n 项和，若0,01716<>S S ，则当nS 最大时n 的值为（）A.8B.9C.10D.16 4.若等差数列{}n a 满足234a S +=，3512a S +=，则47a S +的值是（）A ．20B ．24C ．36D ．72 5. 在ABC D 中，1600==b A ，，其面积为3，则CB A cb a sin sin sin ++++等于（）A ．33B ．3326C ．3392D ．2296.已知实数n m 、满足不等式组ïïîïïíì³£+££+032-42m n m n m n m ，则关于x 的方程()0623-2=++mn x n m x的两根之和的最大值和最小值分别是 （ ）A ．6—，—6B 6 B ．8—，—8C 8 C ．4—，—7D 7 D ．7—，—4 47. 已知正项等比数列}{na 满足：5672a a a +=，若存在两项nm a a 、，使得14a a a n m =，则n m +的值为 ( )A.10B.6C.4D.不存在8.已知{}n a 为等差数列，{}n b 为正项等比数列，公比q ≠1，若111111,a b a b ==，则（ ） A ．66b a = B ．66b a < C ．66b a > D ．66b a <或66b a >9.数列{}()()=^+===+10011,,1,,,,1a b a n a b a n a a a n n n 则且的（ ）A ．99100B ．—99100C ． 100D —．—100 10010. 将正偶数集合{},6,4,2从小到大按第n 组有n 2个偶数进行分组：{}{}{} ,24,22,20,18,16,14,12,10,8,6,4,2，则2120位于第 （ ）组A.33B.32C.31D.3011、数列{}n a 满足21(*)2n n n a a a n N ++=Î，且121,2a a ==，则数列{}n a 的前2011项的乘积为()A ．20122B ． 20112C ．20102D ．2009212、数列{}na 满足2*113,1()2n n n a a a a n N +==-+Î，则122009111m a a a =+++的整数部分是（ ）A ．0B ．1C ．2D ．3第Ⅱ卷（非选择题（非选择题共90分） 二、 填空题（每题5分，共20分。