探究“雪花”曲线
- 格式:doc
- 大小:879.50 KB
- 文档页数:3


科赫曲线
简介
科赫曲线(Koch curve )是一种像雪花的几何曲线,所以又称为雪花曲线。
1904年瑞典数学家科赫第一次描述了这种不论由直段还是由曲段组成的始终保持连通的线,因此将这种曲线成为科赫曲线。
定义
设想一个边长为1的等边三角形,取每边中间的三分之一,接上去一个形状完全相似的但边长为其三分之一的三角形,结果是一个六角形。
现在取六角形的每个边做同样的变换,即在中间三分之一接上更小的三角形,以此重复,直至无穷。
外界的变得原来越细微曲折,形状接近理想化的雪花。
画法
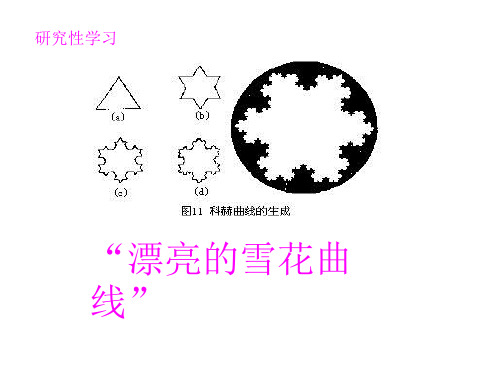
1、任意画一个正三角形,并把每一边三等分;
2、取三等分后的一边中间一段为边向外作正三角形,并把这“中间一段”擦掉;
3、重复上述两步,画出更小的三角形。
4、一直重复,直到无穷,所画出的曲线叫做科赫曲线。
特性
1、它是一条连续的回线,永远不会自我相交。
2、曲线任何处不可导,即任何地点都是不平滑的。
3、曲线是无限长的,即在有限空间里的无限长度。
4、曲线上任意两点距离无穷大。
5、每次变化面积都会增加,但是总面积是有限的,不会超过初始三角形的外接圆。
思考
科赫曲线中产生一个匪夷所思的悖论:"无穷大"的边界,包围着有限的面积。
这让保守派数学大师们都很难相信。
科赫曲线是比较典型的分形图形,它具有严格的自相似特性。
提问:在有限面积里面,无穷的去选择无穷小的点来组成的"封闭"曲线.会包围着无穷大的面积吗?。



科赫曲线总结
科赫曲线是一种分形。
其形态似雪花,又称科赫雪花、雪花曲线。
其豪斯多夫维是。
它最早《关于一条连续而无切线,可由初等几何构作的曲线》。
1.给定线段AB,科赫曲线可以由以下步骤生成:
2.将线段分成三等份(AC,CD,DB)
3.以CD为底,向外(内外随意)画一个等边三角形DMC
4.将线段CD移去
分别对AC,CM,MD,DB重复1~3。
科赫雪花是以等边三角形三边生成的科赫曲线组成的。
科赫雪花的面积是,其中S是原来三角形的边长。
每条科赫曲线的长度是无限大,它是连续而无处可微的曲线。
一、教学背景分析:本节课所学内容可以看作属于高一数学《数列》中的内容,《数列》是人教版教材中第三章的内容,在讲完了等比数列后开设本节研究课。
本节课通过研究大家熟知的雪花,分析它的形状、周长及其面积,来激发大家学习的兴趣,唤起大家对数学美的追求。
同时通过研究雪花曲线,将分形几何的内容逐步渗透到我们的教学中来,为以后的进一步学习打下铺垫。
二、教学目标:1.认知目标:①学会用等比数列解决实际问题;②了解雪花曲线,了解分形几何。
2.能力目标:①培养学生自我探究,自我发现的能力;②利用几何画板自我掌握新知识的能力;③同学之间相互协作的能力。
3.情感目标:①创设问题情境,激发学生学习数学的热情和兴趣;②培养学生对数学美的认识,对美的追求。
三、教法、学法:通过提出问题“雪花的形状如何?”引出话题,激起学生的兴趣,相互讨论得出结论,由老师给出科赫的雪花曲线构成方法,让学生在几何画板环境下作雪花曲线,以探求曲线形状。
雪花曲线的周长及其所围面积可通过讨论由学生来发现计算方法,老师在其中起引导作用。
本节课以学生为主来发现问题、解决问题,通过学生之间的讨论来达到对能力的培养。
四、教学重、难点:重点:对雪花曲线认识及其周长、所围面积的求法。
难点:雪花曲线的周长无限长,而面积是有限的,即无限的曲线围成一个有限的面积的认识。
五、教学程序:(一)创设情景,激起兴趣通过封面的雪花飘落,引出“雪花形状”这个话题,让学生自由探讨,发表自己对雪花的理解,以激起他们对研究雪花的兴趣。
(二)激烈讨论,引出话题曲线生长(5次)当同学们通过讨论,对雪花形状有了一个初步认识之后,由老师给出科赫的构造雪花曲线的方法,让学生使用几何画板作为工具来研究雪花曲线的形状。
雪花曲线是无限生长的,永无止境,老师使用已做好的课件来演示曲线的生长过程,对曲线放大,观察局部,引起学生对曲线自相似...的初步认识。
无限生长的曲线它的周长如何?所围面积如何?提出问题让学生进一步思考。
奇妙的雪花曲线教学目标:(知识目标)1 通过对雪花曲线周长、面积等问题的探究让学生了解数学知识的形成过程;2 使学生了解分形几何的有关内容。
(能力目标)1 通过系列的探究性活动,使学生了解提出和解决数学问题的方法;2 通过对雪花曲线等图形的探究提高学生应用数学的能力。
(情感目标)1 让学生感受数学来源于实践,又服务于实践的辨证唯物主义观点2 通过生活中的具体实例,培养学生对数学美的认识以及对大自然的热爱。
教学重点:探究雪花曲线的周长及其所围面积;教学难点:雪花曲线所围面积的计算方法的寻求;教学方法:引导探究式教学媒体:计算机教学过程设计:1一、问题背景:播放雪景的图片,提问雪花的形状如何,激发学生兴趣。
二、研究问题:如果把雪花想象成如图所示的正六角形,提问学生能否从一个等边三角形出发作出这样的图形。
接着进一步指出,雪花的形状其实非常复杂,右图是瑞典数学家科赫将雪花理想化得到的科赫雪花曲线,提问学生能否仍然从等边三角形出发作出这样的一条雪花曲线,由学生讨论得出:在等边三角形每条边的中央分别向外作等边三角形,边长是原三角形边长的三分之一,就得到了一个六角形。
依照此法,无限制的进行下去,就可以得到漂亮的雪花曲线了。
雪花曲线除了具有漂亮的外形,还蕴涵了哪些数学规律,这就是我们这节课要研究的内容(板书课题)2问题1:对雪花曲线作进一步思考,在雪花曲线的每一次生长中,相对于原三角形都发生了哪些变化,导学生发现它的边长、边数、周长和面积等都发生了变化。
问题2:逐步生长,探究周长的变化规律引导学生发现等边三角形的每一边在生长过程中所发生的变化都是相同的,因此可以只研究其中一条边的变化规律,从而找到解决问题的最优化策略。
让学生自主发现、互相讨论,共同寻找到规律:3得到周长的计算公式后可以提问学生:当n越来越大时,雪花曲线的周长会有什么变化,当原图中三角形的边长为1cm时,显然三角形的周长是3cm,n=33呢,n=82呢, 我们不妨用计算机计算出这样一组数据:n=33时,周长为39819.84cm,约为398米;10 n=82时,周长约为5.27×10cm。
美妙的“雪花曲线”作者:丁学明来源:《课堂内外·创新作文小学版》2011年第01期同学们都以为数学是很一门很古老的科学,有着悠久的历史。
其实,数学也像其他科目一样,是在不断更新和发展的。
其中,分形数学(Fractal Math)就是最近发展起来的一门新的数学分支,到目前为止约有20年的历史,它第一次引起公众注意的是1985年的《科学美国人》上关于Mandelbrot集的一篇文章,自那以后,分形在表现形式和分形几何的理解等方面得到更大进展。
下面就是几个美丽的分形图形:在分形数学中,最典型的当数“雪花曲线”了。
雪花曲线因其形状类似雪花而得名,雪花曲线又名科克曲线,它是在1906年由瑞典数学家赫尔奇·冯·科克第一次作出。
雪花曲线是这样的:由图1那样的等边三角形开始。
然后把三角形的每条边三等分,并在每条边三分后的中段向外作新的等边三角形,但要像图2那样去掉与原三角形叠合的边。
接着对每个等边三角形尖出的部分继续上述过程,即在每条边三分后的中段,像图3那样向外画新的尖形。
不断重复这样的过程,便产生了雪花曲线。
雪花曲线令人惊异的性质是:它具有有限的面积,但却有着无限的周长!要说明它的面积的有限性,要用到高中极限的知识,但是我们可以这样想,在一张纸上画雪花曲线,不管生长多少次,它都不会超过一张纸的,所以说它的面积是有限的。
经过研究,由三角形分形后形成的雪花,其面积等于原三角形面积的1.6倍。
而雪花曲线的周长则可以持续增加而没有界限,所以说它的周长是无限的。
上面我们作的雪花曲线是向外作正三角形,如果我们向内作正三角形,则相应地得到如下图所标示的另一系列的雪花曲线,称之为反雪花曲线。
探究“雪花”曲线
作者:张志勇
来源:《新高考·高二数学》2015年第04期
美丽的分形是大自然景物的抽象,它无比丰富的细节、绚丽多彩的结构常令我们流连忘返,图1中的科赫(Koch)雪花曲线等给我们以美的遐想。
分形在多个领域有着广泛的应用,如物理中的湍流、化学中的高分子链、天文学中的星团分布、地理学中的河流与水系、生物学中的全息现象……
下面我们要探究的是美丽的分形背后的数学身影。
首先,我们来了解一点分形的科普小知识,提及分形,首先要涉及的是其自相似性,所谓自相似性即是指局部是整体成比例缩小的性质,通俗一点,就是当用不同倍数的照相机拍摄研究对象时,无论放大倍数如何改变,看到的照片都是相似的,由此,你能想象Koch雪花曲线的自相似性吗?
雪花曲线由瑞典数学家科赫于1904年构造,因为酷似雪花,所以叫“雪花曲线”,其构造规律是这样的:从图2-1所示的等边三角形开始(称为初始元),将三角形的每条边三等分,并在每条边三分后的中段向外作新的等边三角形(舍去中间的一段,保留两侧的两段,将中间的一段改成夹角为60°的两个等长的直线段,如图2-2),再细分便得到图2-3……不断重复这样的过程,隐去不要的部分,便可得到图1所示的雪花曲线。