奇妙的雪花曲线

科赫曲线-雪花曲线
科赫曲线
科赫曲线是一种外形像雪花的几何曲线，所以又称为雪花曲线，它是分形曲线中的一种，具体画法如下：
1、任意画一个正三角形，并把每一边三等分；
2、取三等分后的一边中间一段为边向外作正三角形，并把这“中间一段”擦掉；
3、重复上述两步，画出更小的三角形。

4、一直重复，直到无穷，所画出的曲线叫做科赫曲线。

和皮亚诺类似：
1、曲线任何处不可导，即任何地点都是不平滑的
2、总长度趋向无穷大
3、曲线上任意两点距离无穷大
4、面积是有限的
5、产生一个匪夷所思的悖论：无穷大的边界，包围着有限的面积。

（保守派数学大师们晕倒撞墙去吧）
Kohn曲线是比较典型的分形图形，它具有严格的自相似特性。

雪花曲线的有趣故事在自然界中，有一种美妙而神奇的现象叫做“雪花曲线”。

这个现象是指雪花的形状会随着温度的变化而改变，从而形成不同的曲线形状。

这个有趣的现象背后隐藏着一段引人入胜的故事。

故事发生在一个寒冷的冬天。

一个年轻的科学家叫做阿尔弗雷德，对雪花的形状变化产生了浓厚的兴趣。

他花了很多时间观察和研究不同温度下雪花的形态。

他发现，当温度越低，雪花的形状就越接近于曲线。

阿尔弗雷德意识到，这种雪花曲线可能是由于水分子在结冰时的特殊排列所致。

他开始进行实验，使用显微镜观察结冰过程中水分子的排列情况。

他发现，水分子在接近冰点的温度下会形成六边形的晶体结构，而在低于冰点的极端寒冷温度下，水分子会形成一种特殊的螺旋排列。

阿尔弗雷德非常激动，他开始将这些发现应用于他的研究当中。

他设计了一个实验装置，通过控制温度的变化来观察雪花的形态。

他发现，当温度处于特定的范围时，雪花的形状会呈现出美丽的曲线，就像被一个无形的艺术家塑造一样。

阿尔弗雷德的研究引起了科学界的广泛关注。

他的成果被认为是对自然界中奇妙现象的重要突破。

人们开始将他的研究应用于气象学和物理学中，以更好地理解和预测天气变化和自然界的规律。

除了科学意义之外，雪花曲线也给人们带来了美学上的享受。

人们开始欣赏雪花的形状和曲线，并将其应用于艺术创作中。

许多艺术家受到雪花曲线的启发，创作出了许多美丽的艺术作品。

雪花曲线的故事告诉我们，自然界中充满了无限的奇迹和美妙。

人类的探索精神和好奇心使得我们能够发现这些奇迹，并将其应用于实践中。

我们应该保持对自然界的敬畏之心，继续探索和研究其中的奥秘，为人类的发展和进步做出贡献。

总之，雪花曲线是一个令人着迷的现象，它不仅让我们对自然界的多样性有了更深的理解，也带给我们美学和艺术上的享受。

这个有趣的故事告诉我们，科学和艺术可以相互交融，创造出更加美好的世界。

一、教学背景分析：本节课所学内容可以看作属于高一数学《数列》中的内容，《数列》是人教版教材中第三章的内容，在讲完了等比数列后开设本节研究课。

本节课通过研究大家熟知的雪花，分析它的形状、周长及其面积，来激发大家学习的兴趣，唤起大家对数学美的追求。

同时通过研究雪花曲线，将分形几何的内容逐步渗透到我们的教学中来，为以后的进一步学习打下铺垫。

二、教学目标：1．认知目标：①学会用等比数列解决实际问题；②了解雪花曲线，了解分形几何。

2．能力目标：①培养学生自我探究，自我发现的能力；②利用几何画板自我掌握新知识的能力；③同学之间相互协作的能力。

3．情感目标：①创设问题情境，激发学生学习数学的热情和兴趣；②培养学生对数学美的认识，对美的追求。

三、教法、学法：通过提出问题“雪花的形状如何？”引出话题，激起学生的兴趣，相互讨论得出结论，由老师给出科赫的雪花曲线构成方法，让学生在几何画板环境下作雪花曲线，以探求曲线形状。

雪花曲线的周长及其所围面积可通过讨论由学生来发现计算方法，老师在其中起引导作用。

本节课以学生为主来发现问题、解决问题，通过学生之间的讨论来达到对能力的培养。

四、教学重、难点：重点：对雪花曲线认识及其周长、所围面积的求法。

难点：雪花曲线的周长无限长，而面积是有限的，即无限的曲线围成一个有限的面积的认识。

五、教学程序：（一）创设情景，激起兴趣通过封面的雪花飘落，引出“雪花形状”这个话题，让学生自由探讨，发表自己对雪花的理解，以激起他们对研究雪花的兴趣。

（二）激烈讨论，引出话题曲线生长（5次）当同学们通过讨论，对雪花形状有了一个初步认识之后，由老师给出科赫的构造雪花曲线的方法，让学生使用几何画板作为工具来研究雪花曲线的形状。

雪花曲线是无限生长的，永无止境，老师使用已做好的课件来演示曲线的生长过程，对曲线放大，观察局部，引起学生对曲线自相似．．．的初步认识。

无限生长的曲线它的周长如何？所围面积如何？提出问题让学生进一步思考。

奇妙的雪花曲线教学目标:(知识目标)1 通过对雪花曲线周长、面积等问题的探究让学生了解数学知识的形成过程;2 使学生了解分形几何的有关内容。

(能力目标)1 通过系列的探究性活动，使学生了解提出和解决数学问题的方法;2 通过对雪花曲线等图形的探究提高学生应用数学的能力。

(情感目标)1 让学生感受数学来源于实践，又服务于实践的辨证唯物主义观点2 通过生活中的具体实例，培养学生对数学美的认识以及对大自然的热爱。

教学重点:探究雪花曲线的周长及其所围面积;教学难点:雪花曲线所围面积的计算方法的寻求;教学方法:引导探究式教学媒体:计算机教学过程设计:1一、问题背景:播放雪景的图片，提问雪花的形状如何,激发学生兴趣。

二、研究问题:如果把雪花想象成如图所示的正六角形，提问学生能否从一个等边三角形出发作出这样的图形。

接着进一步指出，雪花的形状其实非常复杂，右图是瑞典数学家科赫将雪花理想化得到的科赫雪花曲线，提问学生能否仍然从等边三角形出发作出这样的一条雪花曲线,由学生讨论得出:在等边三角形每条边的中央分别向外作等边三角形，边长是原三角形边长的三分之一，就得到了一个六角形。

依照此法，无限制的进行下去，就可以得到漂亮的雪花曲线了。

雪花曲线除了具有漂亮的外形，还蕴涵了哪些数学规律，这就是我们这节课要研究的内容(板书课题)2问题1:对雪花曲线作进一步思考，在雪花曲线的每一次生长中，相对于原三角形都发生了哪些变化,导学生发现它的边长、边数、周长和面积等都发生了变化。

问题2:逐步生长，探究周长的变化规律引导学生发现等边三角形的每一边在生长过程中所发生的变化都是相同的，因此可以只研究其中一条边的变化规律，从而找到解决问题的最优化策略。

让学生自主发现、互相讨论，共同寻找到规律:3得到周长的计算公式后可以提问学生:当n越来越大时，雪花曲线的周长会有什么变化,当原图中三角形的边长为1cm时，显然三角形的周长是3cm，n=33呢,n=82呢, 我们不妨用计算机计算出这样一组数据:n=33时，周长为39819.84cm，约为398米;10 n=82时，周长约为5.27×10cm。

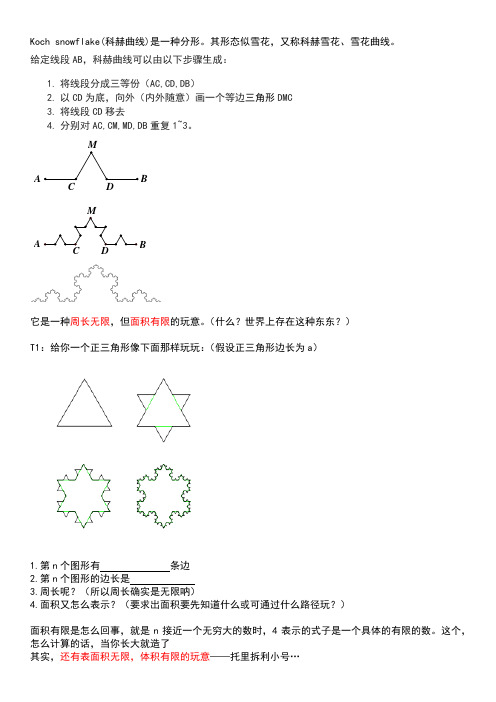
Koch snowflake(科赫曲线)是一种分形。

其形态似雪花，又称科赫雪花、雪花曲线。

给定线段AB ，科赫曲线可以由以下步骤生成： 1. 将线段分成三等份（AC,CD,DB ）
2. 以CD 为底，向外（内外随意）画一个等边三角形DMC
3. 将线段CD 移去
4. 分别对AC,CM,MD,DB 重复1~3。

它是一种周长无限，但面积有限的玩意。

（什么？世界上存在这种东东？）
T1：给你一个正三角形像下面那样玩玩：（假设正三角形边长为a ）
1.第n 个图形有条边
2.第n 个图形的边长是
3.周长呢？（所以周长确实是无限呐）
4.面积又怎么表示？（要求出面积要先知道什么或可通过什么路径玩？）
面积有限是怎么回事，就是n 接近一个无穷大的数时，4表示的式子是一个具体的有限的数。

这个，怎么计算的话，当你长大就造了
其实，还有表面积无限，体积有限的玩意——托里拆利小号… B
A B
A。

初中雪花曲线教案设计说明第一篇：初中雪花曲线教案设计说明初中数学《雪花曲线》教案设计说明民立中学丁海扬一．教材分析1．“雪花曲线”是高中一年级第二学期（试验本）即上海市二期课改新教材中“拓展型课程部分”（拓展内容加“﹡”）内容，供学校自主组织教学和学生选择修习。

2．本节课制定的教学目标是：①知道雪花曲线的生成过程；②学会利用递推关系式得到有关雪花曲线的“问题解决”；③通过对雪花曲线问题的探索与研究以及相关背景资料的介绍，理解数学的价值，感悟数学的美。

3．制定教学目标的几点想法（理论支点）：①教学中应尽可能地显现出数学知识的发生、形成过程；改变传统的注入式（结果型）教学模式，促使学生变接受式（记忆型）学习为自主式（探究型）学习。

②教师应成为学生自主学习和知识建构的促进者；教师的这种“促进者”角色将引导、促进学生的自主学习，使学生能够自己去实验、观察、探究、研讨，使他们的身心全部投入到学习活动之中。

这样的课堂才能充分体现教师的主导作用和学生的主体地位。

③教师并不是以知识的传授为目的，而是以激发学生的问题意识、加深问题的深度、探索解决问题的方法，特别是形成自己对解决问题的独立见解为目的；教师要让学生带着问题走进教室，带着更多的问题走出教室，这就是现今倡导的以问题为纽带的教育教学。

④教学的目的在于不仅希望学生掌握知识，更希望学生掌握分析知识、选择知识、更新知识的能力；简单的说，智慧比知识更重要，过程比结果更重要，知识是启发智慧的手段，过程是结果的动态延伸，教学中能够把结果变为过程，才能把知识变成智慧。

二．教法说明1．以“雪花曲线”的发生过程、“雪花曲线”的问题解决、问题解决方法的简单应用为教学主线，旨在体现：①学习的因是实际，学习的果也是实际；②学习的结果是重要的，但更重要的是学习的过程；③学习的过程是“继承和发扬”，继承就是学习基础，发扬就是学会创新。

2．以介绍“分形几何”（一门新兴的数学分支学科）为教学支线，显现数学知识的文化背景及人文价值。

奇妙的“雪花曲线”
作者：丁学明
来源：《学与玩》2015年第01期
冬季里雪花漫天飞舞，你知道吗，雪不仅是文学艺术领域常常描绘的，也是数学的研究对象。

数学在不断更新和发展，其中，分形数学就是最近发展起来的一门新的数学分支，它第一次引起公众注意是1985年在《科学美国人》上发表的一篇文章，自那以后，分形数学的研究有了许多进展。

在分形数学中，最典型的当数“雪花曲线”了。

雪花曲线因其形状类似雪花而得名，雪花曲线又名科克曲线，它是在1906年由瑞典数学家赫尔奇·冯·科克第一次作出的。

雪花曲线是这样的：由图1那样的等边三角形开始，把三角形的每条边三等分，并在每条边三分后的中段向外作新的等边三角形，但要像图2那样去掉与原三角形叠合的边。

接着对每个等边三角形尖出的部分继续上述过程，即在每条边三分后的中段，像图3那样向外画新的尖形。

不断重复这样的过程，便产生了雪花曲线。

雪花曲线令人惊异的性质是：它具有有限的面积，但却有着无限的周长！我们可以这样想，在一张纸上画雪花曲线，不管“生长”多少次，它都不会超过一张纸的，所以说它的面积是有限的。

经过研究，其面积等于原三角形面积的1.6倍。

而雪花的边长可以无限地增加下去，所以说它的周长是无限的。

上面我们作的雪花曲线是向外作正三角形，如果我们向内作正三角形，则相应地得到如下图所示的另一系列的雪花曲线，称之为反雪花曲线。

下面就是应用分形数学原理画出的两个美丽的分形图形，你能设计出什么样的图形？请你也试着画一下。

如果说有一种平面图形，它的面积是有限的而周长却是无限的，你相信吗？“雪花曲线”就是这样。

那么，什么是“雪花曲线”呢？“雪花曲线”是从一个等边三角形(如图)开始，一步一步作出来的。

第一步：把等边三角形的各边三等分，从每条边三等分后的中段，向外作小等边三角形，再去掉与原来等边三角形重叠的边(如图)。

为了便于叙述，以后把这个过程简称为“变化”。

第二步：对上一步得到的小等边三角形，重复上面的变化(如图)。

第三步：再对上一步得到的小等边三角形，重复上面的变化(如图)。

第四步：再对上一步得到的小等边三角形，重复上面的变化(如图)。

第五步、第六步……照这样一直进行下去，就得到“雪花曲线”。

现在来计算“雪花曲线”(所围成的图形)的面积和周长。

从以上过程可以看出，“雪花曲线”是一个边长、边数不断变化，同一图形边长相等的对称图形。

所以，必须首先研究一下图形的边数、边长和面积的变化规律。

观察发现：规律一：每次变化后，原来等边三角形的一条边，所形成的折线包括4条线段，所以，新图形的边数是原图形的4倍，而边长是原图形的1/3；规律二：每次变化后，原来等边三角形的一条边上，所作的小等边三角形的面积，是原来等边三角形面积的1/9(参看下图)。

一、“雪花曲线”的面积：为了便于计算，设原来等边三角形的面积为“1”。

第一步以后，因为原来的边数是3，向外作了3个小等边三角形；每个小等边三角形的面积是1/9，增加的面积是3×1/9。

第二步以后，边数变成3×4，向外作了3×4个小等边三角形；每个小等边三角形的面积是(1/9)2，增加的面积是3×4×(1/9)2。

第三步以后，边数变成3×42，向外作了3×42个小等边三角形；每个小等边三角形的面积是(1/9)3，增加的面积是3×42×(1/9)3。

第四步以后，边数变成3×43，向外作了3×43个小等边三角形；每个小等边三角形的面积是(1/9)4，增加的面积是3×43×(1/9)4。

3、用《几何画板》生成Koch雪花的制作方法科克(Koch) 雪花：把等边三角形的每一条边三等份，去掉中间的三分之一，在被去掉线段处向外作出两边为此线段三分之一的尖角。

重复这一过程得到各个尖角，以至无穷。

这个几何分形是数学家赫尔奇·冯·科克在1904年创造的。

雪花曲线制作方法1：3.1 打开一个新的绘图窗口，作点A，在水平线上作点B；选择A，双击，标记为旋转中心，按下Shift键，选择点B，从变换菜单中选择旋转命令，弹出对话框，输入“60”，按确定，得点C。

3.2 按下Shift键，依次选择点A、C(点C、B；点B、A)，按下记录对话框中的“快进”键，弹出对话框，“深度”分别选择“1”、“2”、“3”，选择确定，分得图55、图56、图57——2级、3级、4级Koch雪花。

(注意：若依次选择点A、B，则生成的曲线在开始时所作三角形的内部。

)图55 图56 图57作者：江苏省苏州实验中学周建华雪花曲线制作方法2：第1阶段：（1）任取两点AB（2）以点A为中心以(1/3)和(2/3)为比例缩放点B得点C、D（3）以点C为中心将点D旋转60°得到点E（4）选择点C、D、E，选择“构造”菜单中的“三角形内部”命令，构造三角形的内部。

（5）选择三角形的内部，选择“显示”->“颜色”命令，将三角形内部的颜色标为蓝色。

第2阶段：新建一个参数以控制迭代深度，取参数初始值为2第3阶段：（1）选择点A、B、迭代深度，按住<Shift>键不放，然后选择“变换”菜单中的“深度迭代”命令；（2）用鼠标依次选择点D、B建立如图所示A->D，B->B的映射。

第4阶段：（1）选择“结构”->“添加新的映射”命令增加A->E，B->D的新映射；（2）类似地增加如图所示映射。

（3）选择“结构”->“仅没有点的象”命令隐藏由迭代产生的点。

（4）按“迭代”键退出。