下载文档原格式
第四章连续体的振动拉格朗日（grange):1762年建立了离散系统振动的一般理论．对连续系统研究最早的是弦线的振动达朗贝尔（J.le R.d’Alembert)1746年用偏微分方程得到弦线振动的波动方程，并求出行波解伯努利（D.Bernoulli)1753年用无穷多个模态叠加的方法得到了弦线振动的驻波解1759年拉格朗日（grange):从驻波解推得行波解1811年傅里叶提出函数的阶数展开理论，给出严格的数学证明‘其它连续系统的振动问题也相继得到研究伯努利（D.Bernoulli)1744-1751年研究了梁的横向振动，导出了自由.简支和固定端的频率方程和振型函数奇拉尼（E.F.F.Chladni):1802年研究了杆的轴向和扭转振动．本章只讨论理想弹性体的振动理想弹塑性体满足以下假设条件①各向同性；②均质分布；③服从虎克定律§4.1 弦的振动T (,)q x t 讨论两端受到张力拉紧的弦，弦上还受到横向干扰力的作用(,)q x t yxdxxdm Adsρ=第四章连续体的振动设弦的密度为ρ（质量/单位体积）假设小变形，弦力不随挠度变化。
则弦上的任意一点的位移y 应为位置x 与时间t 的函数，即(,)y y x t =22()()dm Ads A dx dy Adxρρρ==+≈(,)(,)y x t x t tg xθθ∂=≈∂y [,]x x dx +沿方向作用在微小区间的外力之和为(,)[(,)](,)(,)(,)(,)x t T x t dx T x t q x t dxxx t T dx q x t dxxθθθθ∂+-+∂∂=+∂根据牛顿第二定律，弦的单元微段ds 沿y 方向的运动微分方程为：22(,)(,)(,)y x t x t Adx T dx q x t dx txθρ∂∂=+∂∂(,)(,)y x t x t xθ∂=∂代入得：2222(,)(,)(,)y x t y x t A T q x t t xρ∂∂=+∂∂22222(,)(,)1(,)y x t y x t c q x t t x Aρ∂∂=+∂∂Tc A ρ=设代入得：C 为波沿长度方向的传播速度(,)()()()sin()n y x t Y x H t Y x t ωϕ==+如无干扰力作用时，22222(,)(,)y x t y x t c t x∂∂=∂∂——称为波动方程弹性体系统作某阶主振动时，其各点也应当作同样的频率及相位运动，各点也应当同时通过静平衡位置和到达最大偏离位置，即系统具有一定的与时间无关的振型()Y x 为振型函数2222222(,)()sin()(,)()sin()nn n y x t Y x t t y x t d Y x t xdx ωωϕωϕ⎧∂=-+⎪⎪∂⎨∂⎪=+⎪∂⎩得2222()()sin()sin()n n n d Y x Y x t c t dx ωωϕωϕ-+=+()sincosnnY x A x B xc c ωω=+(,)(sin cos )sin()n nn y x t A x B x t c cωωωϕ=+⋅+2222()()0n d Y x Y x dxcω+=故,,,n A B ωϕ4个待定常数，可由弦的边界条件及振动的两个初始条件来确定。
第四章连续体的振动§4.2 杆的纵向振动例：有一根 x =0 端为自由、x =l 端处为固定的杆，固定端承受支撑运动 td t u g ωsin )(=d 为振动的幅值试求杆的稳态响应。
l x 0)(t u g §4.2 杆的纵向振动解： l x 0t d t u g ωsin )(=方程建立 dx u dx x u u u g ∂-∂+)(22xu Sdx ∂∂ρdx x F F ∂∂+F 微段分析应变： xu u dx u dx x u u u g g ∂-∂=-∂-∂+=)(])([ε内力： xu u ES ES F g ∂-∂==)(ε达朗贝尔原理： F dx F F u Sdx -∂+=∂)(2ρ),(t x u 杆上距原点 x 处截面在时刻 t 的纵向位移 22)(u u ES u S g -∂=∂ρl x 0td t u g ωsin )(=令： 代入方程： 2222)(x u u ES t u S g ∂-∂=∂∂ρg u u u -=*g u u u +=*即： **''g Su ESu Su ρρ-=-2sin Sd tρωω=-设解为： ∑∞==1*)()(i i i t q x u φ)(x i φ为归一化的正则模态 ,...5,3,1,2cos 2)(==i x li l x i πφ代入方程，得： tSd ESq q S i i i i i ωωρφφρsin )(2,...5,3,1''=-∑∞=l x0t d t u g ωsin )(=2222)(x u u ES t u S g ∂-∂=∂∂ρgu u u -=*∑∞==1*)()(i i i t q x u φ,...5,3,1,2cos 2)(==i x l i l x i πφtSd ESq q S i i i i i ωωρφφρsin )(2,...5,3,1''=-∑∞= )(x j φ用 乘上式，并沿杆长积分：⎰∑⎰⎰=-∞=lj i l j i i l j i idx t Sd dx ES q dx S q 0210''0sin )(φωωρφφφφρ 利用正交性： t d i l l q q i i i i ωωπωsin )1(2222/)1(2--=+l x 0td t u g ωsin )(=2222)(x u u ES t u S g ∂-∂=∂∂ρg u u u -=*∑∞==1*)()(i i i t q x u φ,...5,3,1,2cos 2)(==i x li l x i πφt d i l l q q i i i i ωωπωsin )1(2222/)1(2--=+ 模态稳态解： t d i l l q i i i i ωπηωωsin )1(222/)1(22--=2)/(11i i ωωη-=t lx i d i E l u i i i ωπηπωρsin 2cos )1(16,...5,3,132/)1(322*∑∞=--=l x 0td t u g ωsin )(=2222)(x u u ES t u S g ∂-∂=∂∂ρg u u u -=*2)/(11i i ωωη-=t lx i d i E l u i i i ωπηπωρsin 2cos )1(16,...5,3,132/)1(322*∑∞=--=t d l x i i E l u u u i i i gωπηπωρsin 2cos )1(161 ,...5,3,12/)1(3322*⎥⎦⎤⎢⎣⎡-+=+=∑∞=-小结1. 建立动力学方程2. 根据边界条件求解固有频率和模态3. 变量分离4. 代入动力学方程，并利用正交性条件得到模态空间方程5. 物理空间初始条件转到模态空间6. 模态空间方程求解7. 返回物理空间，得解)()(),(1t q x t x u i i i φ∞=∑=)(2t Q q q j j j j =+ω )(,x i i φω)0(),0(j j q q )(t q j )()(),(1t q x t x u i i i φ∞=∑=物理空间问题 模态空间问题 )()(),(1t q x t x u i i i φ∞=∑=模态叠加法§4.3圆轴的扭转振动取圆轴的轴心线作为x 轴，图示轴任一 x 截面处的转角表示为θ(x ,t ) 。
179第七章 弹性连续体振动的准确解实际的振系都是弹性连续体系统，在很多情况下只是为了使问题简化，计算简便，才把它们简化成前几章所讨论的有限多的离散系统来分析。
当需要对弹性体振动问题作严密的分析时，这时就需要作为连续系统来处理。
弹性连续体问题与离散体问题有不同的特点，弹性连续体的质量、刚度、阻尼是连续分布的，因之具有无限多个自由度，需用无限多个点的独立坐标来表确定，其运动微分方程需要用偏微分方程来描述，而离散体在力学模型上具有明显的集中质量和不计质量的弹性元件，其自由度有限，运动以与自由度个数相等的二阶常系数微分方程来描述。
尽管如此，但两类问题在物理本质上是相同的，若把连续系统的质量分段聚集到有限个点上，各点之间用弹性元件连接起来便成为连续体，反之，离散系统当其质点数趋于无限多时就成为连续体，它们之间有相同的动力特性。
n 自由度连续体系统有n 个固有频率及主振型，而连续体则有无限多个固有频率及主振型，连续体中也存在各个主振型之间关于质量矩阵、刚度矩阵的正交性，对弹性体的响应分析，主振型迭加法有效。
本章将研究具有以下三个条件的理想弹性连续体振动问题的求解：1.材料是均匀的，具有各向同性；2.应力不超过弹性极限、并服从虎克定律；3.变形是微小的且是连续的。
具体是一维弹性体：轴、杆、梁等。
至于其它类弹性连续体如板、壳等的振动问题，因涉及到弹性力学知识，本章将不予讨论。
7-1弦的横向振动先研究最简单的弦的横向振动问题。
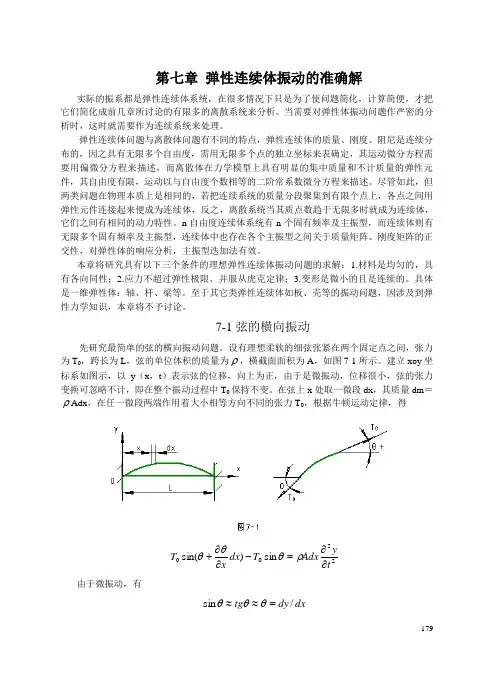
设有理想柔软的细弦张紧在两个固定点之间，张力为T 0，跨长为L ，弦的单位体积的质量为ρ，橫截面面积为A ，如图7-1所示。
建立xoy 坐标系如图示，以y （x ，t ）表示弦的位移，向上为正，由于是微振动，位移很小，弦的张力变换可忽略不计，即在整个振动过程中T 0保持不变。
在弦上x 处取一微段dx ，其质量dm ＝ρAdx ，在任一微段两端作用着大小相等方向不同的张力T 0，根据牛顿运动定律，得2200sin )sin(tyAdx T dx x T ∂∂=-∂∂+ρθθθ由于微振动，有dx dy tg /sin =≈≈θθθ180故有2200)(ty Adx T dx x T ∂∂=-∂∂+ρθθθ代入x y∂∂=θ，简化后，即为 22220ty A x y T ∂∂=∂∂ρ 或写成22222t y a x y ∂∂=∂∂ （7-1） 式中AT a ρ0=称为波沿弦长度方向传播的速度。
连续体系●系统具有连续分布的质量和弹性●物体内材料均匀，各向同性，弹性极限内服从胡克定律●弹性体具有无限多的自由度⏹需要无限多的坐标指定弹性体中任一点的位置●弹性体自由振动可以看成主振型或者正则振型的叠加●对于正则振型的振动，每个颗粒都做简谐振动⏹其频率是相应频率方程的根⏹各颗粒同时经过各自的平衡位置⏹如果物体的运动起始时的弹性曲线精确与每个主振型一致，物体将仅作主振动⏹爆炸或者外力的突然移除导致的弹性曲线，通常与主振动不一致，因而会激起所有振型的振动●在很多情况下，可以通过适当的初始条件激起某个特定的主振型●对于连续质量分布的系统的受迫振动，通过振型叠加法，可以使其转变为有限自由度的系统进行分析●常常把约束作为结构的附加支承来处理⏹会改变系统的主振型●用于表征系统变形的振型不需要一定是正交的●存在使用非正交函数的系统合成⏹例如在进行颤振计算时，为了避免质量变化引起正交振型改变时导致气动力的重新计算，可采用非正交振型，在每次计算中，保持振型不变，而重新计算非对角形式的广义质量矩阵弦的振动●一个柔软的弦，单位长度的质量为，在拉力作用下被张紧●假定其横向挠度很小，挠度引起的张力变化也很小，可以忽略不计●考虑单元长度为的一段弦的受力●挠度和斜率均很小●向的运动方程为●弦的斜率⏹波的扩展速度●一般解可以表示成如下的形式⏹和为任意函数●不管函数的类型如何，对变量微分将得到●如果做变量代换●注意到●简化后●积分两次⏹分量波以速度沿着轴方向移动⏹分量表示波以速度沿着轴方向移动⏹看成是波扩展的速度.●这一方法称为行波法10分离变量法●假定解具有分离变量的形式●代入微分方程后可得●方程左边各项与无关，方程右边各项与无关，因此两边必须是常数●令这个常数为, 得到两个常微分方程●其通解为⏹其中的待定常数, , , 由边界条件和初始条件确定●例题两端固定的张紧的弦，长度为 边界条件为●由●由为波长; 为振动频率的每个值代表一个主振动模态 固有频率为●振型为如下的正弦函数●由任意方式激起的更一般情况的自由振动, 解包括多个振动模态, 位移方程可以写为●应用初始条件and, 可以计算出和●如果把弦拉成任意形状后释放，初始条件可以表示为●每个方程都乘以并从到积分, 方程右边各项除外均为零。
