振动力学与结构动力学-(第一章)
- 格式:ppt
- 大小:1.84 MB
- 文档页数:39


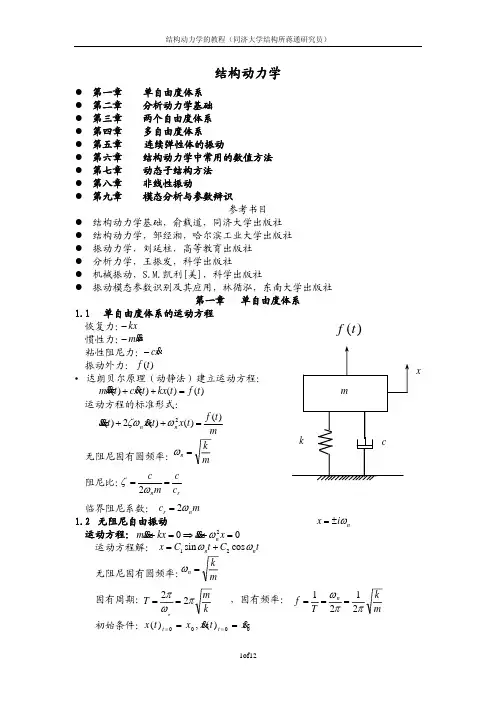




第1章概述研究结构在动荷载作用下的相应规律的学科称为结构动力学结构动力学着重研究结构关于动荷载的响应(如,位移、内力、速度、加速度等的时刻历程)以便确信结构的承载能力和动力学特性,或为改善结构的性能提供依据,结构动力学是抗震设计的基础,也是减震、隔震方法的理论依据。
§结构动力学研究对象与研究目的在动力作用下,结构产生振动,即结构在静平稳位置周围来回地运动(振动)。
振动的缘故,有的是结构本身固有的缘故引发的,如转动机械转子的偏心引发的振动;有的是外界干扰所引发的,如地震作用、风荷载作用,爆炸荷载的作用,和车辆行驶中由于路面不平顺引发的车辆及车辆引发的路面振动等。
因此结构动力学的研究对象正是工程结构的各类振动问题。
而结构动力学的研究目的确实是熟悉和了解工程结构的振动规律,并据此指导工程结构的设计实践及其他有关工作,有效地减轻以幸免有害的振动给工程结构造成破坏,从而为人类社会带来更多的福利,这确实是结构动力学研究的目的和意义。
1.1.1动荷载的概念作用在结构上的荷载是由三个因素确信的,即大小、方向和作用点。
若是这些因素不随时刻转变或随时刻缓慢转变,那么在求解结构的响应时可把其作为静荷载处置加以简化计算,如框架结构的衡宇在自身重力荷载作用下的内力和变形,水塔装满水后的内力和变形等都是结构静力学的范围。
若是作用在结构上的荷载的大小、方向和作用点随时刻转变,使得质量运动加速度所引发的惯性力与荷载相较大到不可轻忽时,那么把这种荷载称为动荷载。
如衡宇结构在风荷载作用下的内力和变形,桥梁结构在汽车荷载作用下的内力和变形,和轮船在海浪的冲击下的内力和变形等都是结构动力学的范围。
应当说明,静与动和加载慢与快是相对的,它与结构自振周期有紧密关系,假设荷载从零增至最大值的加载时刻远大于结构自振周期,例如前者为10s后者为1s,那么加载进程能够为是缓慢的,可作为静荷载对待。
可是假设荷载从零增至最大值的加载时刻接近或小于自振周期,那么加载进程应以为是快速的,这种荷载应作为动荷载来处置。

第一章 单自由度系统1。
1 总结求单自由度系统固有频率的方法和步骤。
单自由度系统固有频率求法有:牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守恒定理法。
1、 牛顿第二定律法适用范围:所有的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析,得到系统所受的合力;(2) 利用牛顿第二定律∑=F x m,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率.2、 动量距定理法适用范围:绕定轴转动的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析和动量距分析;(2) 利用动量距定理J ∑=M θ,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
3、 拉格朗日方程法:适用范围:所有的单自由度系统的振动.解题步骤:(1)设系统的广义坐标为θ,写出系统对于坐标θ的动能T 和势能U 的表达式;进一步写求出拉格朗日函数的表达式:L=T —U ; (2)由格朗日方程θθ∂∂-∂∂∂LL dt )( =0,得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
4、 能量守恒定理法适用范围:所有无阻尼的单自由度保守系统的振动。
解题步骤:(1)对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能T 和势能U 的表达式;进一步写出机械能守恒定理的表达式 T+U=Const (2)将能量守恒定理T+U=Const 对时间求导得零,即0)(=+dtU T d ,进一步得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤.用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。
方法一:衰减曲线法.求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波谷的幅值i A 、1+i A .(2)由对数衰减率定义 )ln(1+=i iA A δ, 进一步推导有 212ζπζδ-=,因为ζ较小, 所以有πδζ2=。

振动力学学习报告引言振动力学课程已经结束了。
在学完整个课程后,我将书本从头看了一边,一来加深自己都知识的掌握,二来将本课程做个总结,使自己掌握的知识能够系统化、结构化。
然后,我将各个部分的知识点总结如下。
第一章 概论一、基本概念1、目的:结构动力学研究结构在动力荷载作用下的位移和内力(统称响应)的分析原理和计算方法,为工程结构设计提供科学依据。
2、基本概念:动力荷载或动荷载(dynamic load )、弹簧力(spring force )、惯性力(inertia force )、阻尼力(damping force )。
3、动力荷载的分类:确定性:确定性动力荷载系指当时间给定后其量值是唯一的。
非确定性:非确定性动力荷载的量值随时间的变化规律不是唯一确定的,而是一个随机过程。
4、研究方法:理论计算方法、试验量测法和计算、试验混合法。
二、结构自由度简化方法1、在结构系统运动的任一时刻,确定其全部质量位置所需的独立几何参变量的个数,称为系统的动力自由度(dynamic freedom )。
2、集中质量法:将连续分布的质量集中到有限个质体上,即把连续分布质量离散成为无重弹性体系上的有限个集中质体。
3、广义位移法:适应于简单结构。
设在t 时刻x 点的位移为y(x,t)将它用一族位移函数的线性和表示∑∞==1)sin()(),(i i l xi t q t x y π,)sin(lx i π为满足位移边界条件的位移函数,)(t q i 为待定参数。
4、有限元法:将实际结构用有限个在结点处相互连接的单元所组成的离散系统代替,对每个单元给定插值函数,然后叠加单元在各个相应结点的贡献建立系统的求解方程。
三、阻尼力1、阻尼:各种能量耗散因素的总称。
在动力计算中,引入一个反应能量耗散的力,称为阻尼力。
2、阻尼力假设:粘性阻尼(viscous damping ):当系统在粘滞性液体中以不大的速度运动时,它所受到的阻尼力大小与速度成正比,而方向和速度的方向相反。

