当前位置：文档之家 › 椭球面上的几种曲率半径

椭球面上的几种曲率半径

  • 格式：ppt
  • 大小：191.00 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

第四讲 椭球面上几种曲率半径讲解材料

第四讲 椭球面上几种曲率半径讲解材料

构成直角三角形
QK Ne 2
OK
Ne 2 sin B
OQ
Ne 2 cos
B
P
W
O
B
E
Q
K
S
P点的法线
第四讲 椭球面上几种曲率半径
一.任意方向法截线曲率半径
（Normal transversal curvature radius at random directions)
1、法截面、法截线的概念
6、公式推导
(1) P-xyz中的椭球面方程
转轴：使两坐标系各轴重合
X ’
（两次转轴)
第一次转轴： P-X’Y’Z’绕Y’ 顺时针旋转(90°+B)，使Z’轴 与P 点的椭球面法线重合，得 坐标系P-X’’Y’’Z’’
Z
X
’
”
P
90°+B Y
Y’
B
Z ”
O
”
K
第一次转轴
第四讲 椭球面上几种曲率半径
6、公式推导
(1) P-xyz中的椭球面方程
第二次转轴
转换关系为
X
x coAs siA n 0x
YRZ(A)ysiA n coAs 0y
Z
z 0 0 1z
X ”
x
PA
yY”
zZ
B”
OO
K 第二次转轴
第四讲 椭球面上几种曲率半径
一.任意方向法截线曲率半径
(Normal transversal curvature radius at random directions)
椭球大地测量学
第四讲 椭球面上几种曲率半径
一系大地测量教研室
第四讲 椭球面上几种曲率半径

子午圈的曲率半径

子午圈的曲率半径
个与该点子午面相垂直的法截面同椭球面相截形成的 闭合的圈，称为卯酉圈。
r N cosB
xra NhomakorabeacosB W
N

a W

N

c V
B B=0o 0o<B<90o B=90o
N
N0=a a<N<c N90=c
说明
卯酉圈即赤道 N↗ B↗
卯酉圈 子午圈
3.主曲率半径的计算 主曲率半径：
子午圈曲率半径M
卯酉圈曲率半径N
级数展开
4.任意法截线的曲率半径
尤拉公式： 1 cos2 A sin2 A
M
RA M
N
RA

N
c os2
MN AM
s in 2
A

1
N 2 cos2
A
N V 2 12 M
A
A
P
N

N
1 e'2 cos2 B cos2 A
说明：
⑴ 法截线的方位角以子午圈的北方向为基准
本节主要内容
• 椭球面上的几种曲率半径
1. 子午圈曲率半径 2. 卯酉圈曲率半径 3. 主曲率半径的计算 4. 任意法截线的曲率半径 5. 平均曲率半径
法截面：过椭球面上任意一点可作一条 垂直于椭球面的法线，包含这条法线 的平面叫法截面。
法截线（弧）：法截面与椭球面的交线 叫法截线。
法截线（弧）上各点处的曲率半径如休 计算？
作业与思考
1. 法截线和法截面定义。 2. M的计算公式。 3. 已知B=36°42´35.2354″，L＝
117°51´43.7653″。 （1）计算M、N、R、c、d的值。 （2）M、N的1秒变化值。 （3）大地方位角为A＝45处法截弧的曲率

地球椭球曲率半径

地球椭球曲率半径

M，N，R的关系
N RM
N90 R90 M 90 c
谢谢观看
cos 2
A
1 e2
cos 2
B cos2
A
椭球的主曲率半径 子午圈曲率半径M 卯酉圈曲率半径Ｎ
第四部分
平均曲率半径
平均曲率半径
平均曲率半径
• 工程应用中，根据测量精度要求，一定范围内，把椭球面当成球面； • 椭球面某点P的所有方向 RA 的平均值作为球体的半径Ｒ；
R MN
或 R b c N a (1 e2 ) W2 V2 V W2
N a W
N c V
第三部分
任意法截弧曲率半径
任意法截弧曲率半径
任意法截弧的曲率半径
• （1）子午法截弧是南北方向，方位角为0°或180° • （2）卯酉法截弧是东西方向，方位角为90°或270° • （3）方位角为Ａ的任意法截弧的曲率半径
1 cos2 A sin 2 A
RA
M
N
N
N
RA
1 2
子午圈曲率半径
2、子午圈曲率半径特点
a(1 e2 ) M
W3
M c V3
N M
V2
B
M
说明
B 0
M 0 a(1 e2 )
c (1 e2 )3
在赤道上，小于赤道半径
0 B 90 B 90
a(1 e2 ) M c
M90
a c 1 e2
随纬度的增大而增大 极点上, 等于极点曲率半径
第二部分
法截线曲率半径都曲率半径（M）
• 子午椭圆的一部分上取一微分弧长 DK ds • 点n是微分弧 dS 的曲率中心 • 于是线段 Dn 及 Kn 便是子午圈曲率半径 M

第7章椭球面讲义上的测量计算

第7章椭球面讲义上的测量计算

(7 31)
B tg1( Z Ne2 sin B) X 2 Y2
(7 32)
H Z N(1 e2 ) sin B
(7 34)
• （7－31）可直接由（7－25）得到。
• （7－32）可根据右图得到。
• OP″＝x＝ X2 Y2
• 因等式右边也包含B，故需迭代计算， 其初始值可设为0; N值也需逐次迭代。
• 归算和改化工作分两步进行。不难理解，椭球体实际上只是一个 过渡体。
• 在第一章中已经简介过参考椭球体的有关概念和参数。本章将比 较系统、详细地介绍椭球体的参数、坐标系以及在椭球面上的测 量计算问题。
• 椭球面上的测量计算公式很多。因时间有限，不一定一一推导。 课堂上讲过的主要公式，未推导部分请同学们课后尽量自学。
• 我国1954年北京坐标系应用的是克拉索夫斯基椭球参数，1980年 西安坐标系应用的是1975年国际椭球参数，而GPS应用的是 WGS-84椭球参数。
• 涉及我国的这三组参数值见表7－1。
克拉索夫斯基椭球
1975年国际椭球
WGS-84椭球
a
6378245 (m)
6378140（m）
6378137 (m)
ab
a
④第一偏心率：e a2 b2 a
⑤第二偏心率： e a2 b2 b
• e和e‫׳‬是子午椭圆的焦点离开中心的距离与椭圆长短半径之比，它 们也能反映椭球体的扁平程度。偏心率越大，椭球愈扁。
• 五个参数中，知道其中的两个就可决定椭球的形状和大小，但其 中至少应有一个是长度元素（如a或b）。习惯上通常用a和α。
计算。参考椭球面是大地测量计算的基准面。
• 椭球体有关元素——
O为椭球中心；
NS为旋转轴；

椭球基本知识

椭球基本知识
大地线旳性质 ➢ 大地线是曲面上两点旳最短线 ➢ 大地线是无数法截线弧素旳连线
控制测量计算理论
六、地面观察值归算至椭球面
3、地面观察方向归算至椭球面 归算旳基本要求 地面观察方向归算至椭球面上有3个基本内容： 1) 将测站点铅垂线为基准旳地面观察方向换算成椭球面上以 法线方向为准旳观察方向； 2) 将照准点沿法线投影至椭球面，换算成椭球面上两点间旳 法截线方向； 3) 将椭球面上旳法截线方向换算成大地线方向。
H H正常 (高程异常)
H H正 N (大地水准面差距)
控制测量计算理论
一、常用旳四种坐标系
2、空间直角坐标系 以椭球中心O为原点，起始子午面与赤道面交线为X轴， 在赤道面上与X轴正交旳方向为Y轴，椭球体旳旋转轴为Z 轴，构成右手坐标系O-XYZ，在该坐标系中，P点旳位置 用X、Y、Z表达 。 空间直角坐标系旳坐标原点位于地球 质心（地心坐标系）或参照椭球中心（参 心坐标系），Z 轴指向地球北极，x 轴指 向起始子午面与地球赤道旳交点，y 轴垂 直于XOZ 面并构成右手坐标系。
4、平均曲率半径
在实际际工程应用中，根据测量工作旳精度要求，在一定范围内，把
椭球面当成具有合适半径旳球面。取过地面某点旳全部方向 RA 旳平均值
来作为这个球体旳半径是合适旳。这个球面旳半径——平均曲率半径R：
R MN 或
R b c N a (1 e2 ) W2 V2 V W2
所以，Ｒ等于该点子午圈曲率半径Ｍ和卯酉圈曲率半径Ｎ旳几何
控制测量计算理论
三、地球椭球及其定位
1、椭球旳几何参数及其关系
e2
a2 b2 a2
e'2
a2 b2 b2
1 e2
b2 a2
1 e2

01 第1章 地球椭球体的基本公式

01 第1章 地球椭球体的基本公式
2 2 2 e
2 e
P1
7
第一偏心率和第二偏心率之间的关系：
e 12
2 e2 = 2 1 + e2
P be E A
O
ae
e
2 2
e = 1 − e12
2 1
E1
P1
8
世界各国常用的地球椭球体数据
椭球名称
埃弗斯特(Everest) 白塞尔(Bessel) 克拉克(Clarke Ⅰ) 克拉克(Clarke Ⅱ) 海福特(Hayford) 克拉索夫斯基(Krassovsky) 1967年大地坐标系 1975年大地坐标系 1980年大地坐标系 WGS84
由（1-2）、（1-3）式可得：
dy b2 x 即 =− 2 dx a y
(1-3)
b2 x = ctgϕ 2 a y
由偏心率公式，可以进一步得到：
(1-4)
a 2 − b2 = e2 a2
即b 2 = a 2 (1 − e 2 )
(1-5)
18
（1-4）式可以化为：
1 y a2 y tgϕ = 2 = b x 1 − e2 x
10
1954年北京坐标系
采用克拉索夫斯基椭球参数，又称北京坐标系。
1980西安坐标系
采用国际地理联合会（IGU）第十六届大会推荐的椭球参数，大地 坐标原点在陕西省泾阳县永乐镇的大地坐标系，又称西安坐标系。
2000国家大地坐标系
采用地心坐标系。
11
§1.2 地球椭球面的基本点、线、面和地理坐标
点
两极 (pole)
SP
6
地球椭球体的形状和大小
扁 率(Flattening or Compression)
fe =

椭圆曲率半径的四种求法

椭圆曲率半径的四种求法

椭圆曲率半径的四种求法
椭圆曲率半径（Elliptic Curvature Radius）是形状参数中重要的一个指标，用来表示计算机显示图形上一定精度的椭圆弧度长度。

椭圆曲率半径是基于椭圆表面距离中心的距离的平均值，它指的是一个椭圆内某点处的曲率半径，即椭圆的曲率半径可用来表示椭圆的形状。

根据椭圆参数方程，椭圆曲率半径可以有以下几种求法。

第一种，基于心形方程求法，其定义为：椭圆曲率半径R = a*b / sqrt((a + b)^2 - c^2)，其中a、b、c分别表示椭圆的长轴、短轴和中心到椭圆上某点距离。

第二种，基于极坐标求法，其定义为：椭圆曲率半径R = (1 + e *cos(2 * theta ) )/(1 + e),其中e表示椭圆的离心率，theta为椭圆上某点的极角。

第三种，基于正弦正切求法，其定义为：椭圆曲率半径R = (a + b ) * (1 + tan^2(theta)) / (a * (1 + tan^2(theta)) + b)，其中a、b为长短轴，θ为椭圆上某点的正切值。

第四种，基于幂级数求法，其定义为：椭圆曲率半径R = [ a^2 * {(1-e^2 + e^4/8)} / {(1-
e^2)^2} + b^2 * {(1-e^2)/4} ] /D,其中a、b分别为长短轴，e为椭圆的离心率，D表示短轴与长轴的比值。

以上是椭圆曲率半径的四种求法。

可以看出，这四种求法的共同初衷都在于对给定的椭圆数据参数，得到椭圆上某点处的曲率半径，进而求得椭圆的形状。

这四种求法各有特点，应用范围也不尽相同，需要根据具体情况和实际应用选择合适的求法，以得到更准确的结果。

中国地质大学(北京)《测量学》期末考试拓展学习(六)80

中国地质大学(北京)《测量学》期末考试拓展学习(六)80

地大《测量学》（六）
第六章 小地区控制测量
椭球面上的测量计算
主要介绍：地球椭球的基本几何参数及相互关系，椭球面上的常用坐标系及其相互关系，椭球面上的几种曲率半径，椭球面上的弧长计算，大地线，将地面观测的方向值归算到椭球面，将地面观测的长度归算到椭球面，椭球面上三角形的解算，大地主题解算的高斯平均引数公式
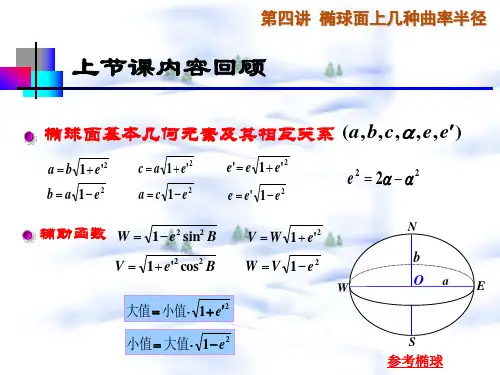
一、地球椭球的基本几何参数及相互关系
（一）、五个基本几何参数
椭圆的长半轴： a
椭圆的短半轴： b
椭圆的扁率：
a b a
α-=
椭圆的第一偏心率：
e b
'= 椭圆的第二偏心率：
e =
注 意
决定旋转椭球的形状和大小，只需知道五个参数中的两个就够了，但其中至少要有一个长度元素（如a 或b ）。

为简化书写，常引入以下符号和两个辅助函数：
2
222,tan ,cos a c t B e B b
η===' 22221sin ,1cos W e B V e B =-=-'
式中，W 第一基本纬度函数，V 第二基本纬度函数。

我国所采用的的1954年北京坐标系应用的是克拉索夫斯基椭球参数；以后采用的1980。

曲率半径

曲率半径

6、公式推导
(3) 任意方向法截线曲率半径
对法截线方程求二阶导数代入曲率半径公式可得
RA N 1 e'2 cos2 A cos2 B
公式说明
RA与L无关 RA与所在的纬度B、法截线方位角A有关 N为P点沿法线方向至椭球短轴的距离PK A为法截线方位角；e’为第二偏心率
第四讲 椭球面上几种曲率半径
(1) 形成
当A=0º 或180º 时，子午圈曲率半径，用M表示
二.子午圈曲率半径
(2) 公式
将A=0º 代入任意方向法截线曲率半径公式
RA N 1 e'2 cos2 A cos2 B
得
M R0
N 1 e 2 cos2 B
第四讲 椭球面上几种曲率半径
（Curvature radius of meridian）
2 2 W 1 e s i n B 2 2 V 1 e' cos B
W、V
W 1 2 V 1 e
M
a (1 e 2 ) c M 3 2 2 (1 e )
说明
在赤道上，M小于赤道半径。 M随纬度的升高而增大，其值 介于a(1-e2)和c之间
6、公式推导
Z
(1) P-xyz中的椭球面方程
两坐标系原点的位置关系：
P XP
ZP B
P2’
O
K
Y
P点在O-XYZ中的坐标
X
X P PP2 N cos B YP 0 2 Z P PP1 N (1 e ) si nB
P1’
P点坐标
第四讲 椭球面上几种曲率半径
N
PK N a W

5地球椭球及数学投影

5地球椭球及数学投影
cos a cos b cos c sin b sin c cos A
A c b
角的余弦公式（四元素）
cos A cos B cosC sin B sin C cos a
O
C B a
正余弦公式（五元素）
sin a cos B sin c cos b cos c sin b cos A sin a cos C sin b cos c cos b sin c cos A sin A cos b sin C cos B cos C sin B cos a sin A cos c sin B cos C cos B sin C cos c
X 说明： KP B 1）ε 为一小正数，如 P3 -10 ； ε =5×10 S 2）J 为迭代收敛时的迭 代次数。 参考椭球
Y
Q
P2
Y
（三）大地坐标与大地空间直角坐标的转换 1、（B，L，H）→（X，Y，Z）
G
N
P0
O L
B
Y
面与椭球赤道的交点方
向 Y轴：构成右手坐标系
X
KP
S
参考椭球
2、大地空间直角坐标系
大地空间直角坐标（X，Y，Z）
N
Z
H L
P
P0
地面点X坐标： OP1 地面点Y坐标： P1 P2
X
G
Z
O
P1
X
B
P2
Y
Y
地面点Z坐标： PP2
KP
S
参考椭球
3、几点补充说明
一个参考椭球（大小+
1940
1975 1996
6378245
6378140 6378137

椭球面上的测量计算

椭球面上的测量计算

控制LO测GO量
三、任意法截弧的曲率半径
❖ 子午法截弧是南北方向，其方位角为00或1800； ❖ 卯酉法截弧是东西方向，其方位角为900或2700，
这两个法截弧在P点上是正交的。
控制LO测GO量
❖ 根据欧拉公式，由曲面上任意一点主曲率半径计算该点任意 方位角A的法截弧的曲率半径的公式为：
1 cos2 A sin2 A
R MN
上式即平均曲率半径的计算公式，表明，曲面任意一点的平均 曲率半径点是该点上主曲率半径的几何平均值。
控制LO测GO量
五、M、N、R的关系
❖ 椭球面上某一点的M、N、R值均是自该点起沿法线向内量取， 其长度通常是不相等的，由前面公式可知它们有如下关系： N>R>M
❖ 只有在极点上，它们才相等，且均等于极曲率半径c，即：
dS DEdx sinB sinB
（dx取负号，是因为在子午 面直角坐标系中，点的横坐 标随纬度B的增大而缩小）
控制LO测GO量
❖两式相代得
dx 1 M
dB sinB
acos2B W
dx dB
a
W
sin
Bcos W2
B
dW dB
W 1e2sin2B
dWd1e2sin2B2e2sinB cosBe2sinB cosB
克拉索夫斯基椭球子午线弧长计算公式：
X 1. 8 1 B 6 1. 4 1 6 1 s 2 8 B 0 3 i 1 . n 8 0 3 4 s 6 4 2 B i 6 0 . 0 n 8 s 6 2 B in 2 X 1 . 8 1 B 3 6 1 . 7 2 s 1 1 B c 8 i B 0 1 3 n o 0 . 9 0 s 3 4 3 s B 2 c i 5 B 3 n 0 . o 6 9 s 5 B s 9 c i B n

椭球面的几何特征与测量计算

椭球面的几何特征与测量计算


4
e2
N
2 m
s2 cos2
Bm
s in 2 A1
a
3

e 2

12N
2 m
s2 cos2
Bm
s in 2 A1
十二 地面观测距离归算至椭球面
W
O
P
X=r
y
QB
y x(1 e2 ) tan B
a
x
cos B
1 e2 sin2 B
E
x
K
N sin B N (1 e2 )sin B e2 N sin B
S
纬度不同，椭球中心到法线与短轴交点之间的距离是不相等的
P
m2
Q1 m1
E
O
n1
n2
既不位于同一平行
圈上，也不位于同
MdB dS cos A rdL dS sin A
A P P2 dB cos A dS dL sin A dS sin A dS
dS P
M
r
N cos B
r N cos B
rdL
O
N P1
rdL N cos BdL
dA
P1T
P1T
90 B
B
P1T N tan( 90 B) N cot B
系数均以米作单位
0.00003m, 0.0003m, R 0.00009m
误差不超过这些舍去项
若将1975年国际椭球的相关参数值代入，还可得到1975年国 际椭球的曲率半径计算式。
五 椭球面上弧长 子午圈弧长公式
M dX dB
X B2 dX B2 MdB

大地测量学基础(椭球面上的几种曲率半径)

大地测量学基础(椭球面上的几种曲率半径)
首先证明：n a和n b 不重合
Ona Q1na sinB1 Onb Q2nbsinB2
b
A
a
B
O B 1 B 2 Q 2
Q1
由 Qn Ne2 ，得
na
Ona N1e2 sinB1
nb
Onb N2e2 sinB2
若 B1B2， Oan Obn
若A、B两点不在同一子午圈上，也不在同一平行圈上时，两点有两条法
⑷了解大地线微分方程和克莱劳定理
—定义：椭球面上两点间的最短程曲线叫大地线。
B
⑴ 大地线是一条空间曲线；
—性质：⑵ 大地线惟一，位于相对法截线之间。
C
—说明：⑴
1 3
A
其长度与法截线长度
相差为百万分之一毫米；
B
⑵地面观测值归算成大地线的
方向，距离。
A
3.大地线的微分方程和克莱劳方程 ⑴ 大地线的微分方程 描述p到p1时，dS与 dA、dL、 dB之间的关系 在微分直角三角形pp2p1中
截线。
说明：⑴相对法截线
A照准B：AaB叫A点的正法截线，B点的反法截线；
B照准A：BbA叫B点的正法截线，A点的反法截线。
⑵ 相对法截线的位置
BbA比AaB偏上。
B2B1， ObnOa， n
正反法截线的位置如课本图4-18 所示
⑶ 当A、B两点位于同一子午圈或平行圈时，正反法截线合 二为一。
⑷ 椭球面上A、B、C三点构不成三角形。（产生了矛盾） 2.大地线的定义和性质
个与该点子午面相垂直的法截面同椭球面相截形成的 闭合的圈，称为卯酉圈。
r N cos B
xr
a cos W
B
N
a W
N

大地测量学知识点分解

大地测量学知识点分解

一、水准面与大地水准面1、水准面我们把重力位相等的面称为重力等位面，也就是我们通常所说的水准面。

水准面有无数个。

1）水准面具有复杂的形状。

2）水准面相互既不能相交也不能相切。

3）每个水准面都对应着唯一的位能W=C=常数，在这个面上移动单位质量不做功，亦即所做的功等于0，即dW=-gsds，可见水准面是均衡面。

4）在水准面上，所有点的重力均与水准面正交。

于是水准面又可定义为所有点都与铅垂线正交的面。

故设想与平均海水面相重合，不受潮汐、风浪及大气压变化影响，并延伸到大陆下面处处与铅垂线相垂直的水准面称为大地水准面大地水准面作为测量外业的基准面，而与其相垂直的铅垂线则是外业的基准线。

似大地水准面与大地水准面在海洋上完全重合，而在大陆上也几乎重合，在山区只有2-4m 的差异我们选择参考椭球面作为测量内业计算的基准面，而与其相垂直的法线则是内业计算的基准线。

1．参心坐标系建立一个参心大地坐标系，必须解决以下问题：(1)确定椭球的形状和大小；(2)确定椭球中心的位置，简称定位；(3)确定椭球中心为原点的空间直角坐标系坐标轴的方向，简称定向；(4)确定大地原点。

我国几种常用参心坐标系：BJZ54、GDZ802．地心坐标系地心坐标系分为地心空间大地直角坐标系和地心大地坐标系等。

地心空间大地直角坐标系又可分为地心空间大地平面直角坐标系和空间大地舜时直角坐标系。

1）建立地心坐标系的意义：2）建立地心坐标系的最理想方法是采用空间大地测量的方法。

3）地心坐标系的表述形式(判断)1）WGS 一84大地坐标系WGS-84坐标系统的全称是World Geodical System-84（世界大地坐标系-84），它是一个地心地固坐标系统。

WGS-84坐标系统由美国国防部制图局建立，于1987年取代了当时GPS 所采用的坐标系统―WGS-72坐标系统而成为GPS 的所使用的坐标系统。

WGS 一84坐标系的几何定义是：坐标系的原点是地球的质心，Z 轴指向BIHl984．0定义的协议地球极(CTP)方向，X 轴指向BIHl984．0的零度子午面和CTP 赤道的交点，y 轴和Z 、X 轴构成右手坐标系。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
上节回顾
• 椭球面上的常用坐标系及其相互关系
一、各种坐标系的建立 1. 大地坐标系 2. 空间直角坐标系 3. 子午面直角坐标系 4. 地心纬度坐标系和归化纬度坐标系 5. 大地极坐标系
上节回顾
二、各坐标系间的关系 1、子午面直角坐标系同大地坐标系的关系 2、空间直角坐标系同子午面直角坐标系的关
系 3、空间直角坐标系同大地坐标系的关系 4、大地纬度 、归化纬度 、地心纬度 之间
的关系
本节主要内容
• 椭球面上的几种曲率半径
1. 子午圈曲率半径 2. 卯酉圈曲率半径 3. 主曲率半径的计算 4. 任意法截线的曲率半径 5. 平均曲率半径
法截面：过椭球面上任意一点可作一条 垂直于椭球面的法线，包含这条法线 的平面叫法截面。
法截线（弧）：法截面与椭球面的交线 叫法截线。
法截线（弧）上各点处的曲率半径如休 计算？
Q k
E A
N Q'
b
O
a
E'
S
4.3 椭球面上的几种曲率半径 1.子午圈曲率半径
M dS

y
dB
dS dx sin B
M dx 1 x acosB/W dB sin B

M

a(1 e2 ) W3
W 1 e2 sin2 B O
K dS
E dx B n dB
个与该点子午面相垂直的法截面同椭球面相截形成的 闭合的圈，称为卯酉圈。
r N cosB
x

r

a
cosB W
N

a W

N

c V
B B=0o 0o<B<90o B=90o
N
N0=a a<N<c N90=c
说明
卯酉圈即赤道 N↗ B↗
卯酉圈 子午圈
3.主曲率半径的计算 主曲率半径：
子午圈曲率半径M
6.M，N，R的关系 N>R>M
在极点处： N90o R90o M 90o c
小结
• 掌握有关概念。 • 掌握(记住)有关计算公式。
回答问题
1. 子午线与子午圈、子午弧 2. 子午圈上，曲率半径变化规律 3. 平行圈曲率半径随纬度变化规律 4. P点纬度为B，哪一条法截弧曲率半径最
大、哪一条法截弧曲率半径最小。
⑵ RA与B有关，与A有关。 当A=0o（或180o）时，RA=M（最小值） 当A=90o（或270o）时，RA=N（最大值） 当A：0o→90o，RA：M→N A：90o→180o，R ：N→M
5.平均曲率半径 平均曲率半径：过椭球面上一点的一切法截弧（从0到 2π），当其数目趋于无穷时，它们的 曲率半径的算术平均值的极限，用R表 示。 计算公式： R MN
作业与思考
1. 法截线和法截面定义。 2. M的计算公式。 3. 已知B=36°42´35.2354″，L＝
117°51´43.7653″。 （1）计算M、N、R、c、d的值。 （2）M、N的1秒变化值。 （3）大地方位角为A＝45处法截弧的曲率
半径。
D x

M

c V3
c a2 b
M

N V2

N

a W
V 1 e'2 cos2 B
B B=0o 0o<B<90o B=90o
M
M0=a(1-e2) a(1-e2)<M<c
M90=c
说明
M0<a M↗ B↗
M90=c
c：极点处（两极）子午圈的曲率半径。 2.卯酉圈曲率半径 卯酉圈：过椭球面上一点的法线，可作无限个法截面。其中一
卯酉圈曲率半径N
级数展开
4.任意法截线的曲率半径
尤拉公式： 1 cos2 A sin2 A
M
RA M
N
RA

N
c os2
MN AM
s in 2
A

1
N 2 cos2
A
N V 2 12 M
A
A
P
N

N
1 e'2 cos2 B cos2 A
说明：
⑴ 法截线的方位角以子午圈的北方向为基准