第四章_2椭球面上几种曲率半径
- 格式:ppt
- 大小:516.00 KB
- 文档页数:24






中学生数理化·教与学2009.12科学思想方法椭圆曲率半径的四种求法◆广西柳州铁一中 温黎明要分析沿曲线运动的质点在曲线上某点的运动情况,往往要先弄清曲线在这一点切线的方向及曲折程度,切线方向可由斜率反映出来,弯曲程度可用极限圆曲率半径反映出来.如果在曲线上某点附近取极短的一段,只要取得足够短,那么,这一小段就可以看成一段很短的圆弧,此圆弧所在的圆叫做曲线在该点的极限圆,极限圆的半径叫曲线在该点的曲率半径.求曲线曲率半径通常用到的依据是向心加速度公式:an =ν2ρ,得ρ=ν2an.故求曲率半径所要解决的问题是:质点经过该位置时速度和在该点法线方向的加速度.对于任意曲线,关键在于如何构建一个合理的模型,使其合运动来满足曲线方程.下面就以求椭圆端点的曲率半径为例,来说明如何构造物理模型.如图1,质点运动的椭圆轨道方程为x2a2+y2b2=1,试用物理的方法求出A(a,0)和B(0,b)两点处的曲率半径.构造模型:将质点的椭圆运动看成两个互相垂直的同频率简谐振动的叠加.解法一:设质点的两个分运动为:x=a s i nωt,y=b c o sωt.它们的合运动的轨道方程就是题中给出的椭圆方程.求速度 νx=aωc o sωt,νy=-bωs i nωt.求加速度 ax=-aω2s i nωt,ay=-bω2c o sωt.在点A处,y=0,x=a;νy =-bω;ax=-aω2,ay=0.由ρ=ν2an解得ρA=b2a.同理可得B点曲率半径ρA =a2b.点评:椭圆的参数方法可以写为x=a s i nωt,y=b c o sωt,此方法将复杂的椭圆运动利用数学中的参数方法,巧妙地分解为两个基本的同频率的简谐振动,将本来没有实际物理意义的参数方程赋予新的物理意义,这样,就简化为讨论两个基本的同121中学生数理化·教与学 2009.12科学思想方法频率的简谐振动问题.利用这个思想,我们可以将任何一个复杂的运动,利用它的参数方程来进行适当的运动分解.从而化复杂为简单,化抽象为具体,这将为我们讨论复杂运动带来很多便利.半径为b 的圆柱面被两平面相截,其中一个平面与圆柱面轴线垂直,第二个平面与第一个平面交角为θ,且满足c o s θ=ba .两平面的交线与圆柱面相切.如图1所示,可得第一个平面与圆柱面的交线是一个半径为b 的圆,第二个平面与圆柱的交线是一个半长轴为a 、半短轴为b 的椭圆.构造模型:将椭圆按上述方法投影成一个圆.解法二:设质点在半径为b 的圆周上作速率为ν的匀速圆周运动,则质点在椭圆上的投影必然沿椭圆轨道运动,轨迹方程就是题中给出的椭圆方程.如图2,点A 速度为ν,法向加速度为ν2b ,点A 的投影A ′的速度和法向加速度为νA ′=νc o s θ=ab ν,(a A ′)n =(a A )n =ν2b .由此可得A ′处的椭圆曲率半径ρA ′=ν2A ′(a A ′)n =a 2b.同理可得B ′处的椭圆曲率半径ρB ′=ν2B ′(a B ′)n =b2b.点评:此方法利用投影的思想,把一个复杂的椭圆运动简化,这是物理学中的一个重要思想.行星绕太阳的运动轨迹为椭圆,同样,我们可以用万有引力的方法来求解.构造模型:设质量为m 的质点在万有引力的作用下绕质量为M 的质点做椭圆运动,轨道的半长轴为a ,半短轴为b ,质量为M 的质点处在椭圆的一个焦点上,如图3.解法三:略.可见,物理模型的建立在物理学习中十分重要.掌握一些物理模型的特点和研究方法,学会将研究对象简化成理想模型、将新的物理情景抽象成我们熟知的物理模型并加以解决,并且于实际情景中构建新的物理模型,这需要大家不断探索和总结.122。

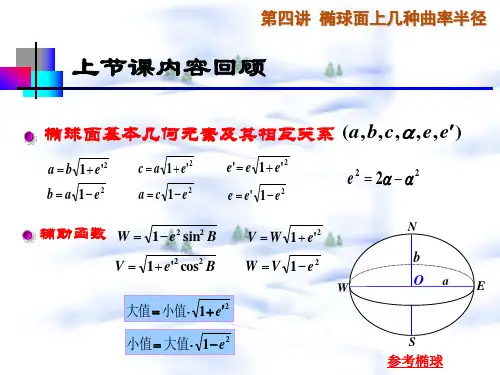


不同高度椭球子午圈曲率半径椭球子午圈曲率半径是地球椭球体上不同纬度处子午圈的曲率半径。
由于地球并非完全规则的球体,它是一个略呈椭圆形的椭球体。
因此,不同纬度处的子午圈曲率半径是不同的。
在本文中,我们将详细介绍椭球子午圈曲率半径的概念、计算方法以及其在地理测量学和地理信息系统中的应用。
首先,我们来了解一下椭球子午圈曲率半径的定义。
椭球是一个既有长轴又有短轴的椭圆体,而子午圈是指一个贯穿地球两极的经线。
由于椭球的形状不规则,子午圈在不同纬度处所形成的曲线也具有不同的弯曲程度,而曲率半径则是反映曲线弯曲程度的一个指标。
接下来,我们来看一下椭球子午圈曲率半径的计算方法。
计算椭球子午圈曲率半径需要使用地球的椭球体参数,包括半长轴(a)和偏心率(e)。
半长轴是地球两个互相垂直的短半轴之一,它的长度约为6378.137千米。
偏心率是一个无单位的常数,用来衡量椭圆体的扁平程度,其取值范围为0到1之间。
计算椭球子午圈曲率半径的公式如下:R = a / (1 - e^2*sin^2(φ))^0.5其中R表示椭球子午圈曲率半径,a表示地球的半长轴,e表示地球的偏心率,φ表示纬度。
根据上述公式,我们可以计算出不同纬度处子午圈的曲率半径。
例如,对于赤道位置(纬度为0),可以代入φ=0进行计算。
由于正弦函数sin(0)的值为0,所以公式化简为:R = a / (1 - e^2*0)^0.5R = a / (1 - 0)^0.5R = a / 1因此,在赤道位置,椭球子午圈曲率半径等于地球的半长轴。
而对于北极位置(纬度为90),可以代入φ=90进行计算。
由于正弦函数sin(90)的值为1,所以公式化简为:R = a / (1 - e^2*sin^2(90))^0.5R = a / (1 - e^2*1)^0.5R = a / (1 - e^2)^0.5因此,在北极位置,椭球子午圈曲率半径等于地球的半长轴除以(1 - e^2)的开方。

椭球面上任意一点的平均曲率半径椭球面是一种非常常见的曲面,它在许多地方都有广泛的应用。
对于椭球面上的任意一点来说,平均曲率半径是一个非常重要的参数。
以下是一个生动、全面、有指导意义的关于椭球面上任意一点的平均曲率半径的文章。
椭球面被用来描述许多物理和数学问题,例如天体运动、地球形状、电子轨道等。
如果我们想要描述椭球面上的任意一点,那么平均曲率半径就是一个非常重要的指标。
平均曲率半径是指,在椭球面上任意一点,沿着任意一个方向取得的曲率半径的平均值。
它既是和形状有关的参数,也是和方向有关的参数。
在椭球面上的一个点上,我们可以取许多不同的方向来计算曲率半径。
平均曲率半径就是将这些曲率半径的值取平均所得到的结果。
如果椭球面上的某一点的平均曲率半径比其他点大,说明这个点的曲率在不同方向上变化很大;如果平均曲率半径比其他点小,说明这个点的曲率在不同方向上相对比较均匀。
平均曲率半径除了可以用于描述椭球面的形状之外,还可以用于计算椭球面上的各种物理量。
例如,在地球科学中,我们可以通过计算地球表面上某一点的平均曲率半径来确定该点的重力场。
在天体物理学中,我们也可以利用平均曲率半径来计算行星或恒星的形状和质量分布情况。
对于椭球面上的每一个点来说,平均曲率半径都是不同的。
因此,我们需要采用一些方法来确定某个点的平均曲率半径。
最常用的方法是利用一些数学公式,例如高斯曲率和曲率半径公式等。
通过这些公式,我们可以计算出椭球面上任意一点的曲率半径,并求取平均值得到平均曲率半径。
总之,平均曲率半径是一个非常重要的参数,它可以用于描述和计算椭球面上的各种物理量。
无论是在地球科学领域还是天体物理学领域,平均曲率半径都有着广泛的应用。
对于研究椭球面的形状和性质来说,平均曲率半径更是一个必不可少的指标。