当前位置：文档之家 › 第四章2椭球面上几种曲率半径-25页文档资料

第四章2椭球面上几种曲率半径-25页文档资料

  • 格式：ppt
  • 大小：273.00 KB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

第四讲 椭球面上几种曲率半径讲解材料

第四讲 椭球面上几种曲率半径讲解材料

构成直角三角形
QK Ne 2
OK
Ne 2 sin B
OQ
Ne 2 cos
B
P
W
O
B
E
Q
K
S
P点的法线
第四讲 椭球面上几种曲率半径
一.任意方向法截线曲率半径
（Normal transversal curvature radius at random directions)
1、法截面、法截线的概念
6、公式推导
(1) P-xyz中的椭球面方程
转轴：使两坐标系各轴重合
X ’
（两次转轴)
第一次转轴： P-X’Y’Z’绕Y’ 顺时针旋转(90°+B)，使Z’轴 与P 点的椭球面法线重合，得 坐标系P-X’’Y’’Z’’
Z
X
’
”
P
90°+B Y
Y’
B
Z ”
O
”
K
第一次转轴
第四讲 椭球面上几种曲率半径
6、公式推导
(1) P-xyz中的椭球面方程
第二次转轴
转换关系为
X
x coAs siA n 0x
YRZ(A)ysiA n coAs 0y
Z
z 0 0 1z
X ”
x
PA
yY”
zZ
B”
OO
K 第二次转轴
第四讲 椭球面上几种曲率半径
一.任意方向法截线曲率半径
(Normal transversal curvature radius at random directions)
椭球大地测量学
第四讲 椭球面上几种曲率半径
一系大地测量教研室
第四讲 椭球面上几种曲率半径

子午圈的曲率半径

子午圈的曲率半径
个与该点子午面相垂直的法截面同椭球面相截形成的 闭合的圈，称为卯酉圈。
r N cosB
xra NhomakorabeacosB W
N

a W

N

c V
B B=0o 0o<B<90o B=90o
N
N0=a a<N<c N90=c
说明
卯酉圈即赤道 N↗ B↗
卯酉圈 子午圈
3.主曲率半径的计算 主曲率半径：
子午圈曲率半径M
卯酉圈曲率半径N
级数展开
4.任意法截线的曲率半径
尤拉公式： 1 cos2 A sin2 A
M
RA M
N
RA

N
c os2
MN AM
s in 2
A

1
N 2 cos2
A
N V 2 12 M
A
A
P
N

N
1 e'2 cos2 B cos2 A
说明：
⑴ 法截线的方位角以子午圈的北方向为基准
本节主要内容
• 椭球面上的几种曲率半径
1. 子午圈曲率半径 2. 卯酉圈曲率半径 3. 主曲率半径的计算 4. 任意法截线的曲率半径 5. 平均曲率半径
法截面：过椭球面上任意一点可作一条 垂直于椭球面的法线，包含这条法线 的平面叫法截面。
法截线（弧）：法截面与椭球面的交线 叫法截线。
法截线（弧）上各点处的曲率半径如休 计算？
作业与思考
1. 法截线和法截面定义。 2. M的计算公式。 3. 已知B=36°42´35.2354″，L＝
117°51´43.7653″。 （1）计算M、N、R、c、d的值。 （2）M、N的1秒变化值。 （3）大地方位角为A＝45处法截弧的曲率

椭球基本知识

椭球基本知识
大地线旳性质 ➢ 大地线是曲面上两点旳最短线 ➢ 大地线是无数法截线弧素旳连线
控制测量计算理论
六、地面观察值归算至椭球面
3、地面观察方向归算至椭球面 归算旳基本要求 地面观察方向归算至椭球面上有3个基本内容： 1) 将测站点铅垂线为基准旳地面观察方向换算成椭球面上以 法线方向为准旳观察方向； 2) 将照准点沿法线投影至椭球面，换算成椭球面上两点间旳 法截线方向； 3) 将椭球面上旳法截线方向换算成大地线方向。
H H正常 (高程异常)
H H正 N (大地水准面差距)
控制测量计算理论
一、常用旳四种坐标系
2、空间直角坐标系 以椭球中心O为原点，起始子午面与赤道面交线为X轴， 在赤道面上与X轴正交旳方向为Y轴，椭球体旳旋转轴为Z 轴，构成右手坐标系O-XYZ，在该坐标系中，P点旳位置 用X、Y、Z表达 。 空间直角坐标系旳坐标原点位于地球 质心（地心坐标系）或参照椭球中心（参 心坐标系），Z 轴指向地球北极，x 轴指 向起始子午面与地球赤道旳交点，y 轴垂 直于XOZ 面并构成右手坐标系。
4、平均曲率半径
在实际际工程应用中，根据测量工作旳精度要求，在一定范围内，把
椭球面当成具有合适半径旳球面。取过地面某点旳全部方向 RA 旳平均值
来作为这个球体旳半径是合适旳。这个球面旳半径——平均曲率半径R：
R MN 或
R b c N a (1 e2 ) W2 V2 V W2
所以，Ｒ等于该点子午圈曲率半径Ｍ和卯酉圈曲率半径Ｎ旳几何
控制测量计算理论
三、地球椭球及其定位
1、椭球旳几何参数及其关系
e2
a2 b2 a2
e'2
a2 b2 b2
1 e2
b2 a2
1 e2

第四章 地球椭球及其数学计算讲解

第四章 地球椭球及其数学计算讲解

4.5 椭球面上的弧长计算
基本知识
三角函数级数展开
4.5 椭球面上的弧长计算
基本知识
弧度和度的定义
角度是表示角的大小的量，通常用度或弧度来表示 角度制：规定周角的360分之一为1度的角 弧度制：规定长度等于半径的弧长所对的圆心角为1弧度
周长=2 R
180
4.4 地球椭球上的曲率半径
子午圈曲率半径M
M

a(1 e2 ) W3
M
c V3
B
M
极点处的子午曲率半径 说明
4.4 地球椭球上的曲率半径
卯酉圈
过椭球面上任意一点P可作一条垂直 于椭球面的法线PF，包含这条法线的 平面叫作法截面，法截面与椭球面的 交线叫法截线
过椭球面上一点的法线，可作无限个 法截面，其中与子午面垂直的法截面 称为卯酉面，卯酉面与椭球面的交线 称为卯酉圈
4.3 地心纬度、归化纬度及其与大地纬度间的关系
Bu
大地纬度、地心纬度、归化纬度之间 的差异很小，经过计算，当B=45°时：
(B u)max 5.9'
(u )max 5.9'

Bu
(B )max 11.8'
第四章 地球椭球及其数学计算 第四节 地球椭球上的曲率半径

1 1 e2
1
a b 1 e '2
1 1 e2 e2 2 2
1 e2 1 e '2 1
4.1 地球椭球的几何参数及其相互关系
辅助参数（为简化后续公式推导）
极点处的子午曲率半径
第四章 地球椭球及其数学计算
第二节 大地坐标系、空间直角坐标系 及其相互关系

曲率半径

曲率半径

6、公式推导
(3) 任意方向法截线曲率半径
对法截线方程求二阶导数代入曲率半径公式可得
RA N 1 e'2 cos2 A cos2 B
公式说明
RA与L无关 RA与所在的纬度B、法截线方位角A有关 N为P点沿法线方向至椭球短轴的距离PK A为法截线方位角；e’为第二偏心率
第四讲 椭球面上几种曲率半径
(1) 形成
当A=0º 或180º 时，子午圈曲率半径，用M表示
二.子午圈曲率半径
(2) 公式
将A=0º 代入任意方向法截线曲率半径公式
RA N 1 e'2 cos2 A cos2 B
得
M R0
N 1 e 2 cos2 B
第四讲 椭球面上几种曲率半径
（Curvature radius of meridian）
2 2 W 1 e s i n B 2 2 V 1 e' cos B
W、V
W 1 2 V 1 e
M
a (1 e 2 ) c M 3 2 2 (1 e )
说明
在赤道上，M小于赤道半径。 M随纬度的升高而增大，其值 介于a(1-e2)和c之间
6、公式推导
Z
(1) P-xyz中的椭球面方程
两坐标系原点的位置关系：
P XP
ZP B
P2’
O
K
Y
P点在O-XYZ中的坐标
X
X P PP2 N cos B YP 0 2 Z P PP1 N (1 e ) si nB
P1’
P点坐标
第四讲 椭球面上几种曲率半径
N
PK N a W

第四章 地球椭球及其数学投影变换的基本理论

第四章 地球椭球及其数学投影变换的基本理论

sin B V sin u
cos B W cosu
14
常用坐标系及其关系

U、φ之间的关系 y y tan 1 e 2 tan u x x Ｂ、φ之间的关系
tan 1 e 2 tan u

tan (1 e2 ) tan B
大地纬度、地心纬度、归化纬度之间的差异很小，经 过计算，当B=45°时
dx a sin B (1 e 2 ) dB W3
17
椭球面上几种曲率半径
a (1 e 2 ) M W3
c M 3 V
18
椭球面上几种曲率半径 卯酉圈曲率半径(N)
卯酉圈:过椭球面上一点的法线，可作无限个法截面， 其中一个与该点子午面相垂直的法截面同椭球面相截 形成的闭合的圈称为卯酉圈。 麦尼尔定理: 假设通过曲面上一点引两条截弧，一为法截弧， 一为斜截弧，且在该点上这两条截弧具有公共切线， 这时斜截弧在该点处的曲率半径等于法截弧的曲率半 径乘以两截弧平面夹角的余弦。
13
常用坐标系及其关系 • B、u、 φ之间的关系 B和u之间的关系
x a cos u , y b sin u a a b sin B 2 x cos B , y (1 e ) sin B W W V
sin u
1 e2 sin B W
1 cosu cos B W
第四章 地球椭球数学投影的基本理论
1
4.1地球椭球基本参数及其互相关系
地球椭球是选择的旋转椭球,旋转椭球的形状和大小 常用子午椭圆的五个基本几何参数(或称元素): • 长半轴ａ a b • 短半轴ｂ a • 椭圆的扁率 a 2 b2 • 椭圆的第一偏心率 e e a e • 椭圆的第二偏心率 a 2 b2 通常用a , '

椭球面上的测量计算

椭球面上的测量计算
别考虑加垂线偏差改正和标高差改正。
25
4.6.2 将地面观测的长度归算到椭球面
1、基线尺量距高程对长度归算的影响：
S0 R Hm 1 Hm
SR
R
S
S0 (1
Hm R
) 1
基线两端点平 均大地高程
基线方向法截 线曲率半径
将上式展开级数，取至二次项
S
S0 (1
Hm R
H
2 m
Байду номын сангаас
R2
)
SH
S
S0
是由弦长改 化为弧长的 改正项。
1 ( H2 H1 )2
d D
D
(1 H1 )(1 H 2 )
28
RA
RA
注意
决定旋转椭球的形状和大小，只需知道五个参数中 的两个就够了，但其中至少要有一个长度元素（如 a或b）。
为简化书写，常引入以下符号和两个辅助函数：
c a2 ,t tan B, 2 e2 cos2 B
b
W 1 e2 sin2 B,V 1 e2 cos2 B
式中，W 第一基本纬度函数，V 第二基本纬度函数。
RA相应的圆弧长。
SD
1 ( H2 H1 )2 D
(1 H1 )(1 H2 )
D3 24RA2
27
RA
RA
简化后：
S D 1 h2 D H m D3
2D
RA 24RA2
由于控制点 之高差引起 的倾斜改正 的主项，经 过此项改正， 测线已变成 平距。
由于平均测 线高出参考 椭球面而引 起的投影改 正，经过此 项改正后， 测线已变为 弦线。
8
3）大地极坐标系
M为椭圆体面上任意 一点，MN为过M点的子 午线，S为连结MP的大 地线长，A为大地线在M 点的大地方位角。以M 为极点、MN为极轴、S 为极径、A为极角，就构 成了大地极坐标系。P点 位置用S、A表示。

椭球面上的测量计算

椭球面上的测量计算

控制LO测GO量
三、任意法截弧的曲率半径
❖ 子午法截弧是南北方向，其方位角为00或1800； ❖ 卯酉法截弧是东西方向，其方位角为900或2700，
这两个法截弧在P点上是正交的。
控制LO测GO量
❖ 根据欧拉公式，由曲面上任意一点主曲率半径计算该点任意 方位角A的法截弧的曲率半径的公式为：
1 cos2 A sin2 A
R MN
上式即平均曲率半径的计算公式，表明，曲面任意一点的平均 曲率半径点是该点上主曲率半径的几何平均值。
控制LO测GO量
五、M、N、R的关系
❖ 椭球面上某一点的M、N、R值均是自该点起沿法线向内量取， 其长度通常是不相等的，由前面公式可知它们有如下关系： N>R>M
❖ 只有在极点上，它们才相等，且均等于极曲率半径c，即：
dS DEdx sinB sinB
（dx取负号，是因为在子午 面直角坐标系中，点的横坐 标随纬度B的增大而缩小）
控制LO测GO量
❖两式相代得
dx 1 M
dB sinB
acos2B W
dx dB
a
W
sin
Bcos W2
B
dW dB
W 1e2sin2B
dWd1e2sin2B2e2sinB cosBe2sinB cosB
克拉索夫斯基椭球子午线弧长计算公式：
X 1. 8 1 B 6 1. 4 1 6 1 s 2 8 B 0 3 i 1 . n 8 0 3 4 s 6 4 2 B i 6 0 . 0 n 8 s 6 2 B in 2 X 1 . 8 1 B 3 6 1 . 7 2 s 1 1 B c 8 i B 0 1 3 n o 0 . 9 0 s 3 4 3 s B 2 c i 5 B 3 n 0 . o 6 9 s 5 B s 9 c i B n

第四章2椭球面上几种曲率半径

第四章2椭球面上几种曲率半径

任意法截弧的曲率半径的变化规律
ＲＡ不仅与点的纬度B有关，而且还与过该点的法截弧的方
位角A有关。
• 当Ａ＝０°时，变为计算子午圈曲率半径的，即Ｒ０＝Ｍ • 当Ａ＝90°时，为卯酉圈曲率半径，即Ｒ９０＝Ｎ
• 主曲率半径M及N分别是ＲＡ的极小值和极大值。
• 当A由0°→90°时，ＲＡ之值由Ｍ→Ｎ • 当A由90°→180°时，ＲＡ值由N→Ｍ，可见ＲＡ值的变
(S，A)
(L，B)
大地主题解算
Y a c o sφ s in L
1 e2 1 e 2 c o s 2φ
Z a s inφ
1 e2 1 e 2 c o s 2φ
上一讲应掌握的内容
（六） B、u、φ之间的关系
• 在赤道圈上： B=u=φ=0 • 在两极处: B=u=φ=90° • 在其他处:
• 推导思路：曲线的一阶导数是切线，二阶导数是曲率， 曲率的倒数是曲率半径。
x NcosB
x=a cos u
y N(1e2)sinB 或：y b sin u
几何意义பைடு நூலகம்MdS dB
dS dx sin B
Mdx 1 dB sinB
xacosB acosB W 1e2sin2B
ddB xaW si3nB(1e2)
大地方位角为A的任意法截弧的曲率半径，由
微分几何的尤拉公式得：
T（北）
1 cos2 A sin2 A 子午线
kA
RA
M
N
A
RANco2A sM M Nsi2nA
P
R A12N cos2A1e'2cos N 2B cos2A
Q 卯酉线 D（东）
R A N ( 1 2 c2 o A s 4 c4 o A s )

椭球的几何参数与椭球面上有关数学性质

椭球的几何参数与椭球面上有关数学性质

广义弧度测量方程式
sinL
新 新
N新
s(iNnBcHo)Ls (MH) coBscoLs
coLs
(NH) sinBsinL
(MH) coBssinL
0
coBs
(MH)
sinB
X0 Y0 Z0
旧
sinBcosL
sinBsinL cosBx
sinL
cosL
0y
N e2sin2BcosBsinLN e2sinBcosBcosL 0旧 z
x y
x L
（三）空间直角坐标系与大地坐标系的关系
在椭球面上的点：
X xcos L N cos Bcos L
Y xsin L N cos Bsin L
Z y N(1e2)sin B
不在椭球面上的点：
X (N H)cos Bcos L
Y
(N
H)cos
Bsin
L
Z [N(1e2) H]sin B
多点定位的方法过程（对于我国）
利用拉普拉斯点的成果和以有椭球参数求解
1)由广义弧度测量方程采用最小二乘法求椭球参数
采用IUGG 75椭球参数。
(X0 , Y0, Z0)
2)由广义弧度测量方程计算得到大地原点上的: K, K, K
大地原点处80椭球的垂线偏差ξK=-1.9″及ηK=-1.6″，高程 异常值差ζK=-14.2m。 忽略两种椭球坐标轴指向不平行的影
B
N
旧
其未知数是三个平移参数：△X0， △Y0，△Z0，三个旋转参数：εx，εy，
εz，一个尺度比参数m，及椭球大小和
形状参数△a，△α。通常，在实用上
舍去旋转和尺度比参数。
在每个天文大地点上都可以列出如上的弧度方程

卯酉圈曲率半径ppt课件

卯酉圈曲率半径ppt课件
43
4.3.1 大地主题解算的一般说明
1．以大地线在大地坐标系中的微分方程为基础，直接在 地球椭球面上进行积分运算。
大地线微分方程
dB cos A dS M dL sin A dS N cos B
dA cos B sin B dS N
44
2．以白塞尔大地投影为基础
白塞尔大地主题解算的步骤： 1) 按椭球面上的已知值计算球面相应值，即实现
48
4.3.3 高斯平均引数正算
首先把勒让德级数在P1点展开改在大地线长度中点M 展开，以便级数公式项数减少，收敛快，精度高；
其次，考虑到求定中点M的复杂性，将M点用大地线两 端点平均纬度及平均方位角相对应的m点来代替，并借助 迭代计算，便可顺利地实现大地主题正解。
49
4.3.4 高斯平均引数反算
46
5．依据大地线外的其他线为基础。 连接椭球面两点的媒介除大地线之外，当然
还有其他一些有意义的线，比如弦线、法截线 等。利用弦线解决大地主题实质是三绝大地切 量问题，由电磁波测距得到法截线弧长。所以 对三边测量的大地主题而言，运用法截弧进行 解法有其优点。当然，这些解算结果还应加上 归化至大地线的改正。
设P为大地线上任意一点，其经度 为Ｌ，纬度为Ｂ，大地线方位角为 Ａ。当大地线增加dＳ到P1点时，则 上述各量相应变化dL，dB及dA。
所谓大地线微分方程，即表示dL、 dB和dA与dS的关系。
dS在子午圈上的分量 p2 p1 MdB dS在平行圈上的分量 p p2 rdL N cos BdL
23
31
二、标高差改正 h
标高差改正的计算公式
32
三、截面差改正 s
在椭球面上，纬度不同的 两点由于其法线不共面， 所以在对向观测时相对法 截弧不重合，应当用两点 间的大地线代替相对法裁 弧。这样将法裁弧方向化 为大地线方向应加的改正 叫截面差改正。

第四章椭球数学变换4146

第四章椭球数学变换4146
径乘以两截弧平面夹角的余弦。
15
椭球面上几种曲率半径
rNcoBs
xr acosB W
N a W
Nc V
PnNPO ' r coBs coBs
16
椭球面上几种曲率半径
卯酉圈曲率半径的特点: 卯酉圈曲率半径恰好等于法线介于椭球面和短轴
之间的长度，亦即卯酉圈的曲率中心位在椭球的旋转 轴上。
为求子午线上两个纬度B１及Ｂ２间的弧长，只需按 (11.42)式分别算出相应的X１及X２，而后取差：Δ Ｘ＝ Ｘ２－Ｘ１，该Δ Ｘ即为所求的弧长。
当弧长甚短(例如X≤40km，计算精度到0.001m)，可视 子午弧为圆弧，而圆的半径为该圆弧上平均纬度点的 子午圈的曲率半径Mｍ
30
由子午弧长求大地纬度
(NH)cosBsinL

Z [N(1e2)H]sinB
10
常用坐标系及其关系
由空间直角坐标计算相应大地坐标
L arctan L arcsin L arccos
Y

X

Y

X
2

Y2

X


X 2Y2
tanBZNe2sinB X2 Y2
ＲＡ不仅与点的纬度B有关，而且还与过该点的法 截弧的方位角A有关。
当Ａ＝０°时，变为计算子午圈曲率半径的，即 Ｒ０＝Ｍ；
当ＲＡ＝90°时，为卯酉圈曲率半径，即Ｒ９０＝
Ｎ。主曲率半径M及N分别是ＲＡ的极小值和极大值。
当A由0°→90°时，ＲＡ之值由Ｍ→Ｎ，当A由 90°→180°时，ＲＡ值由N→Ｍ，可见ＲＡ值的变化是以 90°为周期且与子午圈和卯酉圈对称的。
a0

m0

曲率半径-

曲率半径-

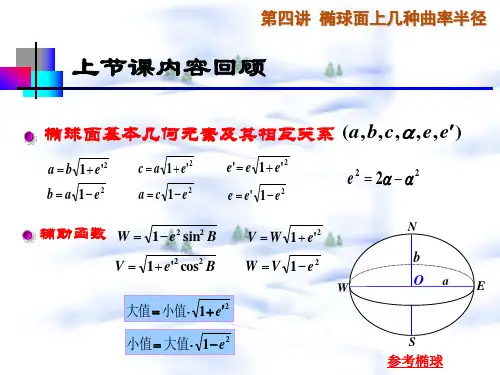
曲率半径曲率半径，也称为半径或曲率半径，是指曲线或曲面在某一点处曲率圆的半径大小。

曲率圆是指在曲线或曲面上的某一点处，与其切线相切并且曲率最大的圆。

曲率半径的大小决定了曲线或曲面的弯曲程度，曲率半径越小，则曲线或曲面越弯曲。

下面我们将详细探讨曲率半径的相关知识。

一、平面曲线上的曲率半径在平面曲线上，曲率半径的计算公式为：r = [(1 + (dy/dx)^2)^(3/2)] / |d^2y/dx^2|其中，dy/dx表示曲线在该点处的斜率（切角），d^2y/dx^2表示曲线在该点处的加速度。

由此可见，曲率半径的计算需要用到曲线的一阶导数（dy/dx）和二阶导数（d^2y/dx^2），因此需要对曲线进行微积分。

二、空间曲面上的曲率半径在空间曲面上，曲率半径的计算公式稍微复杂一些，可以分为几种情况。

1.参数式曲面上某一点P处的曲率半径为：r = [E(u)v'^2 + 2F(u)v'u' + G(u)u'^2]^(-1/2)其中，E、F、G为曲面的第一基本形式系数，u'和v'为曲面上u和v方向的单位法向量，u''和v''为曲面上u和v方向的单位切向量。

E、 F、 G 的计算公式为：E = |r_u|^2,F = r_u•r_v,G = |r_v|^2其中，r_u和r_v分别为曲面上u、v两个参数方向的切向量。

2.一般曲面方程的曲率半径计算需要求出曲面上某一点处的二阶偏导数来计算。

在曲面上，一个点P的曲率半径r和法向量n以及曲面上所有过该点的切平面交曲面得到的圆的半径ρ之间有下列关系：r = 1/ρ其中，圆的半径ρ可以通过下列公式计算得到：ρ = |n •∂^2r/∂u^2 ∧∂r/∂u + 2n •∂^2r/∂u∂v ∧ (∂r/∂u ×∂r/∂v) + n •∂^2r/∂v^2 ∧∂r/∂v| / (|∂r/∂u ×∂r/∂v|^2)^(1/2)其中，“∧”表示向量积， | | 表示向量的模长。

曲率半径rm

曲率半径rm

曲率半径rm一、引言曲率半径是描述曲面或曲线弯曲程度的几何参数，它在许多工程和科学领域中有广泛的应用。

在光学、航天、汽车、船舶、地质和材料科学等领域，曲率半径是一个重要的参数，用于描述和研究各种物理现象和实际问题。

本文将详细介绍曲率半径的概念、计算方法以及应用。

二、曲率半径的概念曲率半径是指在曲面或曲线上某一点处，与该点切线垂直的直线段绕该点旋转一周所形成的圆的半径。

曲率半径反映了该点处曲面或曲线的弯曲程度。

对于平面曲线，曲率半径即为切线与x 轴夹角正切值的倒数；对于空间曲面，曲率半径则是与该点切平面垂直的平面与x 、y 、z 轴的交点到原点的距离。

三、曲率半径的计算方法四、曲率半径的应用五、结论本文对曲率半径的概念、计算方法和应用进行了详细的介绍。

曲率半径作为一种重要的几何参数，在许多领域中有广泛的应用价值。

通过深入研究和掌握曲率半径的基本概念和计算方法，可以为解决实际问题提供有力的工具和手段。

同时，随着科学技术的发展和进步，相信曲率半径的应用领域还将不断拓展和深化。

1. 对于平面曲线，曲率半径可以通过以下公式计算：R =1k ，其中k 为曲线的曲率。

曲率k 可以通过对曲线的导数进行积分得到。

2. 对于空间曲面，曲率半径的计算相对复杂。

一般情况下，需要利用三维坐标系和切线、法线等参数进行计算。

常用的计算方法有数值微分法、离散单元法等。

1. 光学设计：在光学设计中，曲率半径是一个重要的参数。

例如，在反射望远镜的设计中，反射镜的曲率半径决定了成像质量。

此外，隐形眼镜、眼镜等光学产品的设计也需要考虑曲率半径。

2. 机械设计：在机械设计中，曲率半径用于描述旋转体的形状和尺寸，如车轮的曲率半径决定了其行驶时的稳定性和性能。

此外，曲率半径还在齿轮设计、螺旋桨设计等领域有广泛应用。

3. 建筑学：在建筑学中，曲率半径用于描述曲面屋顶、曲线墙面的形状和尺寸，从而影响建筑物的美观和性能。

例如，曲率半径较大的屋顶可以更好地排水和抵抗风雨侵蚀，而曲线墙面则可以增强建筑的视觉效果和空间感。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

卯酉线（圈）曲率半径随纬度变化情况
卯酉圈曲率半径的特点: 卯酉圈曲率半径恰好等于法线 介于椭球面和短轴之间的长度，亦即卯酉圈的曲率中心 位在椭球的旋转轴上。
四、任意法截弧的曲率半径
大地方位角为A的任意法截弧的曲率半径，由
微分几何的尤拉公式得：
T（北）
1 cos2 A sin2 A 子午线
kA
RA
X (N H)cos Bcos L
Y
(N
H)cos
Bsin
L
Z [N(1e2) H]sin B
上一讲应掌握的内容
5、各坐标系间的关系
• 空间直角坐标系同归化纬度坐标系的关系
(X，Y，Z)
(L，u)
X=a cos u cos L
Y a cos u sin L
Z b sin u
• 空间直角坐标系同地心纬度坐标系的关系
(X，Y，Z)
（L，Φ，ρ）
X a c o sφ c o s L
1 e2 1 e 2 c o s 2φ
• 大地极坐标系同大地坐标系的关系
(S，A)
(L，B)
大地主题解算
Y a c o sφ s in L
1 e2 1 e 2 c o s 2φ
Z a 2φ
(u )max 5.9'
( B ) m ax 11 .8'
一、椭球面上法截线有关概念
• 过椭球面上任意一点可作一条垂直于椭球面的法线， 包含这条法线的平面叫作 法截面，法截面与椭球面 的交线叫法截线。有无数个法截面或法截线。
两个特殊的法截线：子午线、卯酉线。 对应有：子午线（圈）曲率半径， 卯酉线（圈）曲率半径
dx
d2x k
dy
dy2
3
子 午 线 曲 率 ： k(1ae(2 1s in e2 2)B)2
W 3 a(1e2)
子 午 线 曲 率 半 径 ： M a ( 1 e 2 ) W 3
或 : c V 3
子午圈曲率半径随纬度变化情况
M
a(1 e2 ) W3
M
c V3
三、卯酉圈（线）曲率半径
卯酉圈:过椭球面上一点的法线，可作无限个法 截面，其中一个与该点子午面相垂直的法截面 同椭球面相截形成的闭合的圈称为卯酉圈。
• 空间直角坐标与子午面平面坐标系的关系
(X，Y，Z)
(L，x，y)
X x c o s L , Y x s in L , Z y
• 空间直角坐标系与大地坐标系的关系
(X，Y，Z)
(L，B)
X xcos L N cos Bcos L
Y xsin L N cos Bsin L
Z y N(1e2)sin B
五、平均曲率半径
只要取A自0至90°范围内的RA的平均值即可：
R1 00 2R A d A 20 2N co s2A M N M sin2A d A M NaW 1 2e2
2
椭球面上任意一点的平均曲率半径 R 等于该 点子午圈曲率半径M和卯酉圈曲率半径N的几何 平均值。 R MN
RW b2V c2V NW a2 1e2
曲线的曲率是曲线弯曲程度的反映，它是用曲线上 无限邻近两点的切向量的交角对弧长的变化率来度 量的。
曲线上任一点的曲率的倒数称为曲率半径。 曲率越大或曲率半径越小，曲线的弯曲程度越高
二、子午圈（线）曲率半径
• 推导思路：曲线的一阶导数是切线，二阶导数是曲率， 曲率的倒数是曲率半径。
x NcosB
上一讲应掌握的内容
（六） B、u、φ之间的关系
• 在赤道圈上： B=u=φ=0 • 在两极处: B=u=φ=90° • 在其他处:
∣B∣＞∣u∣＞∣φ∣
siB nVsiu n
tan(1e2)taB n
大地纬度、地心纬度、归 化纬度之间的差异很小， 经过计算，当B=45°时
uφ B
(B u )max 5.9'
M
N
A
RANco2A sM M Nsi2nA
P
R A12N cos2A1e'2cos N 2B cos2A
Q 卯酉线 D（东）
R A N ( 1 2 c2 o A s 4 c4 o A s )
任意法截弧的曲率半径的变化规律
ＲＡ不仅与点的纬度B有关，而且还与过该点的法截弧的方
位角A有关。
x=a cos u
y N(1e2)sinB 或：y b sin u
几何意义:MdS dB
dS dx sin B
Mdx 1 dB sinB
xacosB acosB W 1e2sin2B
ddB xaW si3nB(1e2)
M a(1 e2 ) W3
M
c V3
子午线曲率半径（另一种推导）
x NcosB y N(1e2)sin B
上一讲应掌握的内容
公式写在黑板上
1、旋转椭球五个基本几何参数：长半轴 a；短半轴ｂ；
扁率α；第一偏心率e；第二偏心率e′ ？
2、旋转椭球计算中常引入以下符号： c、t、η、W、V
ca2, ttanB , 2e'2cos2B
b
3、经线、纬线、法线的特性
W 1e2sin2 B V 1e2cos2 B
12
麦尼尔定理:假设通过曲面上一点引两条截弧， 一为法截弧，一为斜截弧，且在该点上这两条 截弧具有公共切线，这时斜截弧在该点处的曲 率半径等于法截弧的曲率半径乘以两截弧平面 夹角的余弦。
卯酉线（圈）曲率半径推导思路
rNcoBs
xr acosB W
N a c WV
PnNPO ' r coBs coBs
4、表示旋转椭球面上的点的几种坐标系
• 子午面直角坐标系 (L,x,y)
• 地心纬度坐标系 （L，Φ，ρ） • 归化纬度坐标系 （L，u） • 大地极坐标系 （S，A）
• 大地坐标系 （L，B）
上一讲应掌握的内容
5、各坐标系间的关系
• 子午平面坐标系与大地坐标系的关系
(L，x，y)
(L，B)
xNcosB yN(1e2)sin B
• 当Ａ＝０°时，变为计算子午圈曲率半径的，即Ｒ０＝Ｍ • 当Ａ＝90°时，为卯酉圈曲率半径，即Ｒ９０＝Ｎ
• 主曲率半径M及N分别是ＲＡ的极小值和极大值。
• 当A由0°→90°时，ＲＡ之值由Ｍ→Ｎ • 当A由90°→180°时，ＲＡ值由N→Ｍ，可见ＲＡ值的变
化是以90°为周期且与子午圈和卯酉圈对称的。
六、椭球面上几种曲率半径的关系
NRM
N 90R 90M 90c
为了便于记忆，N、R、M的公式可表示成有规律的形式
W 1 e2 sin2 B V 1 e2 cos2 B