18、轴向拉压杆的强度计算解析

轴向拉压杆件内力计算公式在工程力学中，轴向拉压杆件是一种常见的结构元件，它在工程实践中被广泛应用于各种机械设备和建筑结构中。

轴向拉压杆件内力计算公式是用来计算轴向拉压杆件在受力作用下内部产生的拉力或压力的公式，它是工程设计和分析中非常重要的一部分。

在本文中，我们将介绍轴向拉压杆件内力计算公式的推导和应用，希望能够帮助读者更好地理解和应用这一重要的工程知识。

一、轴向拉压杆件的受力分析。

轴向拉压杆件是一种受拉或受压的结构元件，它通常由材料制成，具有一定的截面形状和尺寸。

当轴向拉压杆件受到外部力的作用时，内部会产生拉力或压力，这种内力的大小和方向是由外部力和结构本身的特性共同决定的。

在进行轴向拉压杆件的内力计算时，需要先进行受力分析，确定受力情况和受力方向。

通常情况下，轴向拉压杆件受到的外部力可以分为两种情况，拉力和压力。

对于受拉的轴向拉压杆件，外部力的方向和内部拉力的方向相同；对于受压的轴向拉压杆件，外部力的方向和内部压力的方向相反。

在受力分析的基础上，可以得到轴向拉压杆件内力计算的基本公式：N = A σ。

其中，N为轴向拉压杆件的内力，A为截面积，σ为应力。

根据受力分析的结果，可以确定σ的正负号，从而确定N的正负号，进而确定内力的方向。

二、轴向拉压杆件内力计算公式的推导。

1. 受拉的轴向拉压杆件。

对于受拉的轴向拉压杆件，外部拉力的方向和内部拉力的方向相同，因此内力的大小可以直接由外部拉力计算得到。

假设外部拉力为P，截面积为A，根据胡克定律，可以得到应力σ=P/A，进而得到内力N=P。

因此，受拉的轴向拉压杆件内力计算公式为：N = P。

2. 受压的轴向拉压杆件。

对于受压的轴向拉压杆件，外部压力的方向和内部压力的方向相反，因此内力的大小需要考虑结构的稳定性。

假设外部压力为P，截面积为A，根据胡克定律，可以得到应力σ=P/A，进而得到内力N=P。

然而，受压的轴向拉压杆件在实际应用中往往需要考虑结构的稳定性，因此需要引入材料的材料的屈服强度和稳定性系数，从而得到更加精确的内力计算公式。

轴向拉、压杆的强度计算教学设计基于中职、中专类学生的特点，我选用的是高教出版社《土木工程力学基础》，该书在内容上对原有的冗杂部分进行了删减，在满足教学需要的同时，符合中专生以就业为导向的培养思想。

力学课是一门技术基础课，本课的学习主要是为学生学习专业课做铺垫的，所以十分重要。

所以结合教学大纲的要求及学生层次特点，本课的教学重难点为：【教学重难点】教学重点：理解正应力拉压干强度公式含义教学难点：利用拉压杆强度条件公式解决强度效和、截面设计等工程实际问题。

【教学目标】1. 技能目标：使学生能够应用正应力强度条件公式完成轴向拉压构件强度校核、截面设计和确定许用荷载方面的实际任务。

2.能力目标：加强学生解决问题的能力。

3.情感目标：在探究学习中增强学生的自信。

这样多元化的教学目标，把关键的能力培养蕴含于知识技能的学习中专，并培养他们自信的心理态度。

【教学过程】科学合理的教学方法能使教学效果事半功倍，达到教与学的和谐完美统一。

因为我们所面对的学生的学习基础薄弱，学习方法单一，习惯于被动接受，而非主动思考，而本节课又是理论性极强的一节课，所以我采用的教法是以任务驱动法为主线贯穿整堂课，各部分穿插讲授法、演示教学法、启发教学法。

而学法上，我贯彻的指导思想是以提高和发展学生的能力为本，启发引导学生积极思考探究问题，发现规律，看到本质，纳未知为已知；倡导“自主、合作、探究”的学习方式，具体的学法是自主学习、探究学习、小组合作完成任务法和分组讨论法。

我的教学过程的开展以任务驱动的形式为主要的教学方法贯穿于课程始终。

在完成任务课题探讨阶段分别使用了范例式教学法和启发式教学法，使学生通过自主学习、探究学习、合作学习的学习方式理解新课知识点。

整个过程强调提高和发展学生的能力为本，其中贯穿了引导、启发的思想，充分发挥教师主导的同时，体现学生主体的教学理念，下面我对具体的教学过程进行做一下阐释。

为了完成教学目标，解决教学重点突破教学难点，课堂教学我按四个大模块、七个教学环节展开来完成教学过程。

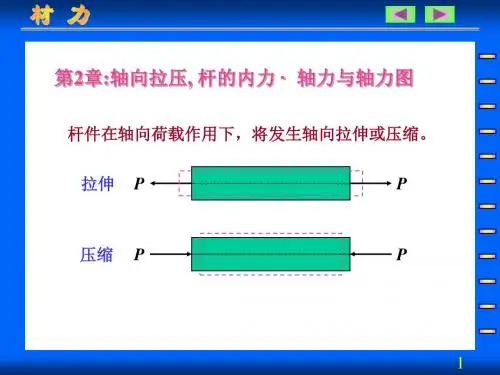
第九章杆件的强度分析与计算第一节概述一、构件的承载能力机械或机器的每一组成部分称为构件，它是机器的运动单元，为保证构件正常工作，构件应具有足够的能力负担所承受的载荷。

因此，构件应当满足以下要求：（一）、强度要求：构件在外力作用下应具有足够的抵抗破坏的能力。

在规定的载荷作用下构件不应被破坏,具有足够的强度。

例如，冲床曲轴不可折断；建筑物的梁和板不应发生较大塑性变形。

强度要求就是指构件在规定的使用条件下不发生意外断裂或塑性变形。

（二）、刚度要求：构件在外力作用下应具有足够的抵抗变形的能力。

在载荷作用下，构件即使有足够的强度，但若变形过大，仍不能正常工作。

例如，机床主轴的变形过大，将影响加工精度；齿轮轴变形过大将造成齿轮和轴承的不均匀磨损，引起噪音。

刚度要求就是指构件在规定的使用条件下不发生较大的变形。

（三）、稳定性要求：构件在外力作用下能保持原有直线平衡状态的能力。

承受压力作用的细长杆，如千斤顶的螺杆、内燃机的挺杆等应始终维持原有的直线平衡状态，保证不被压弯。

稳定性要求就是指构件在规定的使用条件下有足够的稳定性。

为满足以上三方面的要求，构件可选用较好的材料和较大的截面尺寸，但这与节约和减轻构件自相矛盾。

构件设计的任务就是在保证满足强度、刚度和稳定性要求的前提下，以最经济的方式，为构件选择适宜的材料、确定合理的形状和尺寸。

二、变形固体的基本假设由各种固体材料制成的制成的构件在载荷作用下将产生变形，称为变形固体或变形体。

为了便于理论分析和实际计算，对变形固体常采用的几个基本假设：（一）．连续性假设：假设在固体所占有的空间内毫无空隙地充满了物质。

实际上，组成固体的粒子之间存在空隙，但这种空隙极其微小，可以忽略不计。

于是可认为固体在其整个体积内是连续的。

基于连续性假设，固体内的一些物理量可用连续函数表示。

（二）．均匀性假设：均匀性假设是指材料的力学性能在各处都是相同的，与其在固体内的位置无关。

（三）．各向同性假设：即认为材料沿各个方向的力学性质是相同的。