2014年秋季新版华东师大版九年级数学上学期23.5、位似图形同步练习

23.5 位似图形知识点 1 位似图形1．位似图形的位似中心可以在( ) A ．原图形外 B ．原图形内C ．原图形的边上D ．以上三种都有可能 2．下列说法正确的是( ) A ．相似图形一定是位似图形 B ．位似图形一定是相似图形 C ．全等的图形一定是位似图形 D ．位似图形一定是全等图形3．下列图形中，不是位似图形的是( )图23－5－1知识点 2 位似图形的性质4．如果两个多边形是位似图形，它们的相似比为2∶5，那么这两个多边形的周长之比是______________，面积之比是________．5．［xx·绥化］如图23－5－2，△A ′B ′C ′是由△ABC 以点O 为位似中心经过位似变换得到的，若△A ′B ′C ′的面积与△ABC 的面积比是4∶9，则OB ′∶OB 等于( )A. 2∶3 B ．3∶2 C ．4∶5 D ．4∶9图23－5－26．如图23－5－3所示，矩形ABCD 中，AB ＝9，BC ＝6，若矩形AEFG 与矩形ABCD 位似，且相似比为23，则点C ，F 之间的距离为( )A. 13 B ．2 13 C. 3 13 D ．12图23－5－3知识点 3 位似图形的相关作图7．如图23－5－4，已知△EFH 和△MNK 是位似图形，那么其位似中心是( )图23－5－4A．点A B．点B C．点C D．点D8．如图23－5－5所示，在下列由作位似图形的方法得到的图形中，其相似比为2的是( )图23－5－59．如图23－5－6，以点O为位似中心，将△ABC放大，使新图形与原图形的相似比为2∶1.图23－5－610．如图23－5－7，△DEF是由△ABC经过位似变换得到的，位似中心是点O，请确定点O的位置，如果OC＝3.6 cm，OF＝2.4 cm，求出它们的相似比．图23－5－711．如图23－5－8所示，在平面直角坐标系中，有两点A(4，2)，B(3，0)，以原点为位似中心，A′B′与AB的相似比为12，得到线段A′B′.正确的画法是( )图23－5－812．如图23－5－9，以点O为位似中心，将边长为256的正方形OABC依次作位似变换，经第一次变换后得正方形OA 1B 1C 1，其边长OA 1缩小为OA 的12，经第二次变换后得正方形OA 2B 2C 2，其边长OA 2缩小为OA 1的12，经第三次变换后得正方形OA 3B 3C 3，其边长OA 3缩小为OA 2的12，…，依此规律，经第n 次变换后，所得正方形OA n B n C n 的边长为正方形OABC 边长的倒数，则n ＝________．图23－5－913．［教材习题23.5第2题变式］［xx·天等县一模］如图23－5－10，在6×8的网格中，每个小正方形的边长均为1，点O 和△ABC 的顶点均在小正方形的顶点上．(1)在△ABC 的内部作△A ′B ′C ′，使△A ′B ′C ′和△ABC 位似，且位似中心为点O ，相似比为1∶2；(2)连结(1)中的AA ′，则线段AA ′的长度是________．图23－5－1014．印刷一张矩形的广告ABCD ，如图23－5－11所示，它的印刷面积(四边形A ′B ′C ′D ′)是32 cm 2，上、下空白各1 cm ，左、右空白各0.5 cm ，设印刷部分从上到下(A ′B ′)的长是x cm.(1)当要求四周空白处的面积为18 cm 2时，求用来印刷这张广告的纸张的长和宽各是多少； (2)在(1)的条件下，内外两个矩形是位似图形吗？请说明理由．15．如图23－5－12，用下面的方法可以画△AOB 的内接等边三角形，阅读后证明相应问题． 画法：①在△AOB 内画等边三角形CDE ，使点C 在OA 上，点D 在OB 上；②连结OE 并延长，交AB 于点E ′，过点E ′作E ′C ′∥EC ，交OA 于点C ′，作E ′D ′∥ED ，交OB 于点D ′；③连结C ′D ′.则△C ′D ′E ′是△AOB 的内接三角形．求证：△C ′D ′E ′是等边三角形．图23－5－121．D2．B 3．D 4．2∶5 4∶25 5．A 6．A 7．B 8．B 9．略10．解：连结AD ，CF 交于点O ，则点O 即为所求． ∵OC ＝3.6 cm ，OF ＝2.4 cm ， ∴OC ∶OF ＝3∶2，∴△ABC 与△DEF 的相似比为3∶2.11．D 12．1613．解：(1)如图，△A ′B ′C ′即为所作．(2) 514． (1)由题意得2×x ×0.5＋2×32x×1＋4×1×0.5＝18.∵x ≠0，∴x 2－16x ＋64＝0，∴(x －8)2＝0，∴x ＝8(负值已舍去)． 经检验x ＝8符合题意． ∴x ＋2＝10，32x＋1＝5.答：用来印刷这张广告的纸张的长是10 cm ，宽是5 cm.(2)是位似图形．理由：∵外面矩形的长与宽之比为105＝2，里面矩形的长与宽之比为84＝2，故两图形相似，且知四对对应顶点的连线都经过同一点，∴内外两个矩形是位似图形．15．证明：由题意知△OEC ∽△OE ′C ′，△ODE ∽△OD ′E ′，∴OC OC ′＝OE OE ′＝CE C ′E ′＝DE D ′E ′＝OD OD ′. ∵OC OC ′＝OD OD ′，∠COD ＝∠C ′OD ′， ∴△COD ∽△C ′OD ′， ∴OC OC ′＝CD C ′D ′，∴CEC′E′＝DED′E′＝CDC′D′，∴△CDE∽△C′D′E′.∵△CDE是等边三角形，∴△C′D′E′是等边三角形．（本资料素材和资料部分来自网络，供参考。

23.5 位似图形1．若是两个图形对应点的连线__交于一点__，而且各对对应点与那个交点所连线段的比值__相等__，那么这两个图形叫做位似图形，那个交点叫做__位似中心__．2．判定位似图形必需具有三个条件：(1)两个图形__相似__；(2)对应点的连线__相交于一点__；(3)对应边相互__平行__或在__同一条直线上__．3．位似图形必然是相似图形；位似图形上任意一对对应点到位似中心的距离之比等于__相似比__．知识点1：位似图形的概念1．以下3个图形中是位似图形的有( B )A．1个B．2个C．3个D．0个2．(2021·东营)以下关于位似图形的表述：①相似图形必然是位似图形，位似图形必然是相似图形；②位似图形必然有位似中心；③若是两个图形是相似图形，且每组对应点的连线所在的直线都通过同一个点，那么，这两个图形是位似图形；④位似图形上任意两点与位似中心的距离之比等于位似比．其中正确命题的序号是( A) A．②③ B．①② C．③④ D．②③④3．图中两个四边形是位似图形，它们的位似中心是( D )A．点M B．点N C．点O D．点P知识点2：位似图形的性质4．两个图形中，对应点到位似中心的线段比为2∶3，那么这两个图形的相似比为( A )A．2∶3 B．4∶9C.2∶ 3 D．1∶25．如图，四边形ABCD与四边形AEFG是位似图形，且AC∶AF＝2∶3，那么以下结论不正确的选项是( B ) A．四边形ABCD与四边形AEFG是相似图形B．AD与AE的比是2∶3C．四边形ABCD与四边形AEFG的周长比是2∶3D．四边形ABCD与四边形AEFG的面积比是4∶9,第5题图) ,第6题图)6．如图，以点O 为位似中心，将五边形ABCDE 放大后取得五边形A ′B ′C ′D ′E ′，已知OA ＝10 cm ，OA ′＝20 cm ，那么五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比值是__12__．知识点3：位似图形的画法7．如图，找出以下图形的位似中心O .解：略8．如图，已知形如木屋架的五边形ABCDE ，点O 在BC 上，以O 点为位似中心把ABCDE 缩小到原先的12.解：略9．(2021·玉林)△ABC 与△A′B′C′是位似图形，且△ABC 与△A′B′C′的位似比是1∶2，已知△ABC 的面积是3，那么△A′B′C′的面积是( D )A ．3B ．6C ．9D ．1210．如图，五边形ABCDE 和五边形A 1B 1C 1D 1E 1是位似图形，且PA 1＝23PA ，则AB ∶A 1B 1等于( B )A.23B.32C.35D.5311．用作位似图形的方式，能够将一个图形放大或缩小，位似中心位置可选在( D ) A ．原图形的外部 B ．原图形的内部 C ．原图形的边上 D ．任意位置12．如图，以下由位似变换取得的图形中，面积比是1∶9的是( D )13．如图，△ABC 与△A ′B ′C ′是位似图形，点O 是位似图形，若OA ＝2AA ′，S △ABC ＝8，则S △A ′B ′C ′＝__18__． 14．如图，△ABC 与△A ′B ′C ′是位似图形，且位似比是1∶2，若AB ＝2 cm ，则A ′B ′＝__4__cm ，并在图中画出位似中心O .解：图略15．如图，已知△DEO 与△ABO 是位似图形，△OEF 与△OBC 是位似图形，试说明：OD ·OC ＝OF ·OA .解：由△DEO 与△ABO 位似取得OD OA ＝OE OB ；由△OEF 与△OBC 位似可得OE OB ＝OF OC .∴OD OA ＝OFOC ，即OD·OC ＝OF·OA16．如图，图中的小方格都是边长为1的正方形，△ABC 与△A ′B ′C ′是关于点O 为位似中心的位似图形，它们的极点都在小正方形的极点上．(1)画出位似中心点O ；(2)求出△ABC 与△A ′B ′C ′的位似比；(3)以点O 为位似中心，再画一个△A 1B 1C 1，使它与△ABC 的位似比等于1.5.解：(1)略 (2)1∶2 (3)画图略，寻觅A 1，B 1，C 1的方式是OA OA 1＝OB OB 1＝OC OC 1＝23即可17．如图，在6×8的网格图中，每一个小正方形的边长均为1，点O 和△ABC 的极点均为小正方形的极点．(1)以O为位似中心，在网格图中作△A′B′C′，使△A′B′C′和△ABC位似，且相似比为1∶2；(2)连接(1)中的AA′，求四边形AA′C′C的周长．(结果保留根号)解：(1)如图（2）四边形AA′C′C的周长＝4＋62。

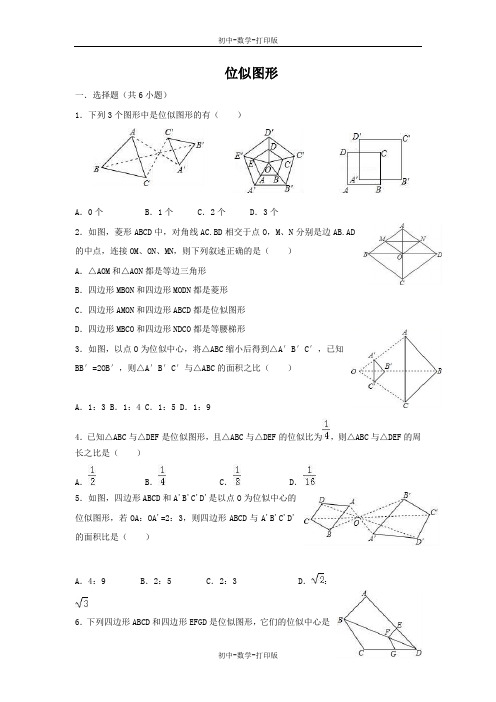
位似图形一．选择题（共6小题）1．下列3个图形中是位似图形的有（）A．0个B．1个C．2个D．3个2．如图，菱形ABCD中，对角线AC.BD相交于点O，M、N分别是边AB.AD的中点，连接OM、ON、MN，则下列叙述正确的是（）A．△AOM和△AON都是等边三角形B．四边形MBON和四边形MODN都是菱形C．四边形AMON和四边形ABCD都是位似图形D．四边形MBCO和四边形NDCO都是等腰梯形3．如图，以点O为位似中心，将△ABC缩小后得到△A′B′C′，已知BB′=2OB′，则△A′B′C′与△ABC的面积之比（）A．1：3 B．1：4 C．1：5 D．1：94．已知△ABC与△DEF是位似图形，且△ABC与△DEF的位似比为，则△ABC与△DEF的周长之比是（）A． B． C． D．5．如图，四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形，若OA：OA'=2：3，则四边形ABCD与A'B'C'D'的面积比是（）A．4：9 B．2：5 C．2：3 D．：6．下列四边形ABCD和四边形EFGD是位似图形，它们的位似中心是（）A．点E B．点F C．点G D．点D二．填空题（共6小题）7．把一个三角形变成和它位似的另一个三角形，若边长缩小到倍，则面积缩小到原来的倍．8．如图，△ABC与△DEF位似，位似中心为点O，且S△ABC=S△DEF，则AB：DE的值为9．在由边长为1的正三角形组成的正六边形网格中画一个与已知△ABC相似但不全等的三角形．10．如图，以点O为位似中心，将△ABC缩小得到△A′B′C，若AA′=2OA′，则△ABC与△A′B′C′的周长比为__________．11．如图，矩形ABCD与矩形A′B′C′D′是位似图形，A是位似中心，已知矩形ABCD的周长为24，BB′=4，DD′=2．求AB和AD的长．12．如图，四边形ABCD与四边形EFGH位似，位似中心是点O，若=，则=__________．三．解答题（共4小题）13．已知如图，点P是边长为4的正方形ABCD内一点，且PB=3，BF⊥BP于B，请在射线BF 上找一点M，使以B.M、C为顶点的三角形与△ABP相似．14．在4×4的方格中，△ABC的三个顶点都在格点上．（1）在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形（画出一个即可）；（2）在图2、图3中各作一格点D，使得△ACD∽△DCB，并请连结AD.CD.BD．15．如图，在6×6的正方形方格中，每个小正方形的边长都为1，顶点都在网格线交点处的三角形，△ABC是一个格点三角形．（1）在图①中，请判断△ABC与△DEF是否相似，并说明理由；（2）在图②中，以O为位似中心，再画一个格点三角形，使它与△ABC的位似比为2：1 （3）在图③中，请画出所有满足条件的格点三角形，它与△ABC相似，且有一条公共边和一个公共角．16．在4×6的方格中（1）画出与格点△ABC相似的△DEF（相似比不为1，且顶点应在格点上）；（2）证明你的结论．参考答案一．选择题1．D．2．C．3．D．4．B．5．A．6．D．二．填空题7．．8．2：3．9．如图所示，△A′BC即为所求．10．3：1．11． 8， 4．12．．三．解答题13．解：∵四边形ABCD为正方形，PB⊥BF，∴∠ABC=∠PBF=90°，∴∠ABP+∠PBC=∠PBC+∠CBF，∴∠ABP=∠CBF，当△ABP∽△CBM时，则有=，即=，解得BM=3；当△ABP∽△MBC时，则有=，即=，解得BM=；∴BM=3或．14．解：（1）如图所示：（2）如图所示：△ACD∽△DCB．15．解：（1）如图①所示：△ABC与△DEF相似，理由：∵AB=1，BC=，AC=2；DE=，EF=，DF=4，∴====，∴△ABC与△DEF相似；（2）如图②所示：△A′B′C′即为所求；（3）如图③所示：△ADC和△CEB即为所求．16．解：（1）如图，△DEF为所作；（2）证明如下：∵AB=4，BC==2，AC==2，DE=2，EF==，DF==，∴==， ==， ==，∴==，∴△DEF∽△ABC．。

23.5 位似图形同步测试题（满分120分；时间：120分钟）班级____________姓名___________成绩_________一、选择题（本题共计10 小题，每题3 分，共计30分，）1. 如图两个三角形是位似图形，它们的位似中心是（）A.点B.点C.点D.点2. 如图所示，，，，分别是，，，的中点，已知四边形的面积是，则四边形的面积是（）A. B. C. D.3. 如图，和是位似图形，且是的中点，则等于（）A. B. C. D.4. 与是位似图形，且对应边与之比为，则的周长与的周长之比为（）A. B. C. D.5. 如图，是以点为位似中心经过位似变换得到的，若的面积与的面积比是，则为( )A. B. C. D.6. 如图，与是位似图形，且相似比为，若的面积为，则的面积为（）A. B. C. D.7. 如图，与是位似图形，点是位似中心，若，，则等于（）A. B. C. D.8. 如图，已知点，点，以为位似中心，把放大为原来的倍，则点的对应点坐标为（）A.或B.或C. D.9. 已知与是关于点的位似图形，它们的对应点到点的距离分别为和，则与的面积比为（）A. B. C. D.10. 在平面直角坐标系中，已知，，以原点为位似中心，按位似比把缩小，则点的对应点的坐标为（）A. B.C.或D.或二、填空题（本题共计8 小题，每题3 分，共计24分，）11. 如图，点，，分别是三边中点，则与是以________为位似中心的位似图形．12. 已知：如图，，，的延长线交于于点，与是________图形，其中________点是位似中心．13. 如图，与为位似图形，点是它们的位似中心，位似比是，且的面积为，那么的面积是________．14. 在平面直角坐标系中，顶点的坐标为，若以原点为位似中心，画的位似图形，使与的相似比等于，则点的坐标________．15. 与是位似图形，且与的位似比是，已知的面积是，则的面积是________．16. 如图，在大小为的正方形方格中，的顶点、、在单位正方形的顶点上，请在图中画一个，使（相似比不为），且点、、都在单位正方形的顶点上．________．17. 将一个多边形放大为原来的倍，则放大后的图形可作出________个，其原因是________．18. 如图，在的正方形网格中，点、、、、都在小正方形的顶点上，试在该网格中找点，连接、，使得与相似，且点与点对应，点与点对应．________．三、解答题（本题共计8 小题，共计66分，）19. 如图，在上，、相交于点，且，（1）图中有哪几对位似三角形，选其中一对加以证明；（2）若，，求的长．20. 如图，已知是原点，、两点的坐标分别为、．（1）以点为位似中心，在轴的左侧将放大两倍（即新图与原图的位似比为），画出图形并写出点、的对应点的坐标；（2）如果内部一点的坐标为，写出的对应点的坐标．21. 如图，如果，，那么与是位似三角形吗？为什么？22. 如图，在正方形网格中，有，，三个格点．试在图中再找出一个格点，满足：与，，三点中的两点组成的三角形恰好与相似．请找出三种不同方案画出符合题意的三角形，并写出所画三角形与的面积比．23. 如图所示，以点为似中心，将放大到原来的倍，画出图形写出，的坐标，求的面积．24. 如图，已知与是位似图形，求证：．25. 如图，矩形与矩形是位似图形，已知矩形的周长是，，，求矩形和的面积比．26. 如图，在平面直角坐标系中，的顶点坐标分别为，，．以原点为位似中心，在轴的右侧将放大为原来的两倍得到．（1）画出；（2）分别写出，两点的对应点，的坐标．。

一、选择题1. 如图，线段CD两个端点的坐标分别为C〔1，2〕、D〔2，0〕，以原点为位似中心，将线段CD放大得到线段AB，假设点B坐标为〔5，0〕，那么点A的坐标为〔〕A.〔2，5〕B．〔2.5，5〕C．〔3，5〕D．〔3，6〕第1题图第2题图第3题图2. 如图，以点O为位似中心，将△ABC放大得到△DEF．假设AD=OA，那么△ABC与△DEF的面积之比为〔〕A.1：2 B．1：4 C．1：5 D．1：63. 如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABO 与△A′B′O′是以点P为位似中心的位似图形，它们的顶点均在格点〔网格线的交点〕上，那么点P的坐标为〔〕A.〔0，0〕B．〔0，1〕C．〔-3，2〕D．〔3，-2〕4. 如图，△ABC经过位似变换得到△DEF，点O是位似中心且OA=AD，那么△ABC与△DEF的面积比是〔〕A.1：6 B．1：5 C．1：4 D．1：25. ，如图，E〔-4，2〕，F〔-1，-1〕．以O为位似中心，按比例尺1：2把△EFO缩小，点E的对应点的坐标〔〕第4题图第5题图第6题图A.〔-2，1〕B．〔2，-1〕C．〔2，-1〕或〔-2，-1〕D．〔-2，1〕或〔2，-1〕6. 如图，△DEF与△ABC是位似图形，点O是位似中心，D、E、F分别是OA、OB、OC的中点，那么△DEF与△ABC的面积比是〔〕A.1：6 B．1：5 C．1：4 D．1：27. 如图，己知△ABC，任取一点O，连AO，BO，CO，并取它们的中点D，E，F，得△DEF，那么以下说法正确的个数是〔〕①△ABC与△DEF是位似图形；②△ABC与△DEF是相似图形；③△ABC与△DEF的周长比为1：2；④△ABC与△DEF的面积比为4：1．A.1 B．2 C．3 D．4第7题图第8题图第11题图8. 如图，线段AB的两个端点坐标分别为A〔1，1〕，B〔2，1〕，以原点O 为位似中心，将线段AB放大后得到线段CD．假设CD=2，那么端点C的坐标为〔〕A.〔2，2〕B．〔2，4〕C．〔3，2〕D．〔4，2〕9. 将三角形三个顶点的横坐标都乘以2，纵坐标不变，那么所得三角形与原三角形的关系是〔〕B．与原点对称C．纵向不变，横向拉长为原来的二倍 D．关于y轴对称10. 以下说法中：①位似图形一定是相似图形；②相似图形一定是位似图形；③两个位似图形假设全等，那么位似中心在两个图形之间；④假设五边形ABCDE 与五边形A′B′C′D′E′位似，那么在五边形中连线组成的△ABC与△A′B′C′也是位似的．正确的个数是〔〕A.1 B．2 C．3 D．411. 如下图，正方形EFGH是由正方形ABCD经过位似变换得到的，点O是位似中心，E，F，G，H分别是OA，OB，OC，OD的中点，那么正方形EFGH与正方形ABCD的面积比是〔〕A.1：6 B．1：5 C．1：4 D．1：212. 如图，菱形ABCD中，对角线AC、BD相交于点O，M、N分别是边AB、AD的中点，连接OM、ON、MN，那么以下表达正确的选项是〔〕A.△AOM和△AON都是等边三角形B．四边形MBON和四边形MODN都是菱形C．四边形AMON和四边形ABCD都是位似图形D．四边形MBCO和四边形NDCO都是等腰梯形第12题图第13题图13. 以下说法正确的选项是〔〕B．两个位似图形对应点连线交点个数为1或2C．两个位似图形对应点连线只有一个交点D．两个位似图形对应点连线交点个数不少于4个14. 用作位似形的方法，可以将一个图形放大或缩小，位似中心〔〕A.只能选在原图形的外部B．只能选在原图形的内部C．只能选在原图形的边上 D．可以选择任意位置15. 如图，四边形ABCD与四边形AEFG是位似图形，且AC：AF=2：3，那么以下结论不正确的选项是〔〕B．AD与AE的比是2：3C．四边形ABCD与四边形AEFG的周长比是2：3D．四边形ABCD与四边形AEFG的面积比是4：9二、填空题16. 在直角坐标系中，△ABC的坐标分别是A〔-1，2〕，B〔-2，0〕，C〔-1，1〕，假设以原点O为位似中心，将△ABC放大到原来的2倍得到△A′B′C′，那么落在第四象限的A′的坐标是________17. 在平面直角坐标系中，点A〔-4，2〕，B〔-2，-2〕，以原点O为位似中心，把△ABO放大为原来的2倍，那么点A的对应点A′的坐标是18. 如图，△ABC中，点D、E、F分别是AB、BC、AC的中点，那么与△ADF 位似的三角形是．第18题图第19题图第20题图19. 如图，点A〔0，1〕，B〔-2，0〕，以坐标原点O为位似中心，将线段AB 放大2倍，放大后的线段A′B′与线段AB在同一侧，那么两个端点A′，B′的坐标分别为20. 如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上．〔1〕△ABC的面积等于；〔2〕假设四边形DEFG是△ABC中所能包含的面积最大的正方形，请你在如下图的网格中，用直尺和三角尺画出该正方形，并简要说明画图方法〔不要求证明〕三、解答题21. 在平面直角坐标系中，△ABC的三个顶点坐标分别为A〔2，-4〕，B〔3，-2〕，C〔6，-3〕．〔1〕画出△ABC关于x轴对称的△A1B1C1；22. 点P为线段AB上一点，射线PM⊥AB，用直尺和圆规在PM上找一点C，使得PC2=AP•PB．23. 如图，在平面直角坐标系中，△ABC的三个顶点坐标系分别为A〔-2，1〕，B〔-1，4〕，C〔-3，-2〕．〔1〕以原点O为位似中心，位似比为1：2，在y轴的左侧，画出△ABC放大后的图形△A1B1C1，并直接写出C1点坐标；〔2〕如果点D〔a，b〕在线段AB上，请直接写出经过〔1〕的变化后点D 的对应点D1的坐标．24. 如图，在平面直角坐标系中，四边形OABC的顶点坐标分别是O〔0，0〕，A〔3，0〕，B〔4，4〕，C〔-2，3〕，将点O，A，B，C的横坐标、纵坐标都乘以-2．〔1〕画出以变化后的四个点为顶点的四边形；〔2〕由〔1〕得到的四边形与四边形OABC位似吗？如果位似，指出位似中心及与原图形的相似比．25. 如下图，图中的小方格都是边长为1的正方形，△ABC与△A′B′C′是以点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上．〔1〕画出位似中心点O；〔2〕直接写出△ABC与△A′B′C′的位似比；〔3〕以位似中心O为坐标原点，以格线所在直线为坐标轴建立平面直角坐标系，画出△A′B′C′关于点O中心对称的△A″B″C″，并直接写出△A″B″C″各顶点的坐标．参考答案一、选择题1. 如图，线段CD两个端点的坐标分别为C〔1，2〕、D〔2，0〕，以原点为位似中心，将线段CD放大得到线段AB，假设点B坐标为〔5，0〕，那么点A的坐标为〔〕A.〔2，5〕B．〔2.5，5〕C．〔3，5〕D．〔3，6〕答案：B解析：解答：∵以原点O为位似中心，在第一象限内，将线段CD放大得到线段AB，∴B点与D点是对应点，那么位似比为：5：2，∵C〔1，2〕，∴点A的坐标为：〔2.5，5〕应选：B分析：利用位似图形的性质结合对应点坐标与位似比的关系得出A点坐标．2. 如图，以点O为位似中心，将△ABC放大得到△DEF．假设AD=OA，那么△ABC与△DEF的面积之比为〔〕A.1：2 B．1：4 C．1：5 D．1：6答案：B解析：解答：∵以点O为位似中心，将△ABC放大得到△DEF，AD=OA，∴OA：OD=1：2，∴△ABC与△DEF的面积之比为：1：4．应选：B．分析：利用位似图形的性质首先得出位似比，进而得出面积比．3. 如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABO 与△A′B′O′是以点P为位似中心的位似图形，它们的顶点均在格点〔网格线的交点〕上，那么点P的坐标为〔〕A.〔0，0〕B．〔0，1〕C．〔-3，2〕D．〔3，-2〕答案：C解析：解答：如下图：P点即为所求，故P点坐标为：〔-3，2〕．应选：C．分析：利用位似图形的性质得出连接各对应点，进而得出位似中心的位置．4. 如图，△ABC经过位似变换得到△DEF，点O是位似中心且OA=AD，那么△ABC与△DEF的面积比是〔〕A.1：6 B．1：5 C．1：4 D．1：2答案：C解析：解答：∵△ABC经过位似变换得到△DEF，点O是位似中心且OA=AD，∴AC∥DF，∴△OAC∽△ODF，∴AC：DF=OA：OD=1：2，∴△ABC与△DEF的面积比是1：4．应选C．分析：由△ABC经过位似变换得到△DEF，点O是位似中心且OA=AD，根据位似图形的性质，即可得AC∥DF，即可求得AC：DF=OA：OD=1：2，然后根据相似三角形面积的比等于相似比的平方，即可求得△ABC与△DEF的面积比．5. ，如图，E〔-4，2〕，F〔-1，-1〕．以O为位似中心，按比例尺1：2把△EFO缩小，点E的对应点的坐标〔〕A.〔-2，1〕B．〔2，-1〕C．〔2，-1〕或〔-2，-1〕 D．〔-2，1〕或〔2，-1〕答案：D解析：解答：∵E〔-4，2〕，以O为位似中心，按比例尺1：2把△EFO缩小，∴点E的对应点的坐标为：〔-2，1〕或〔2，-1〕．应选D．分析：由E〔-4，2〕，F〔-1，-1〕．以O为位似中心，按比例尺1：2把△EFO缩小，根据位似图形的性质，即可求得点E的对应点的坐标．6. 如图，△DEF与△ABC是位似图形，点O是位似中心，D、E、F分别是OA、OB、OC的中点，那么△DEF与△ABC的面积比是〔〕A.1：6 B．1：5 C．1：4 D．1：2答案：C解析：解答：∵△DEF与△ABC是位似图形，点O是位似中心，D、E、F分别是OA、OB、OC的中点，∴两图形的位似之比为1：2，那么△DEF与△ABC的面积比是1：4．应选C．分析：根据两三角形为位似图形，且点O是位似中心，D、E、F分别是OA、OB、OC的中点，求出两三角形的位似比，根据面积之比等于位似比的平方即可求出面积之比．7. 如图，己知△ABC，任取一点O，连AO，BO，CO，并取它们的中点D，E，F，得△DEF，那么以下说法正确的个数是〔〕①△ABC与△DEF是位似图形；②△ABC与△DEF是相似图形；③△ABC与△DEF的周长比为1：2；④△ABC与△DEF的面积比为4：1．A.1 B．2 C．3 D．4答案：C解析：解答：根据位似性质得出①△ABC与△DEF是位似图形，②△ABC与△DEF是相似图形，∵将△ABC的三边缩小的原来的1 2，∴△ABC与△DEF的周长比为2：1，故③选项错误，根据面积比等于相似比的平方，∴④△ABC与△DEF的面积比为4：1．应选C．分析：根据位似图形的性质，得出①△ABC与△DEF是位似图形进而根据位似图形一定是相似图形得出②△ABC与△DEF是相似图形，再根据周长比等于位似比，以及根据面积比等于相似比的平方，即可得出答案．8. 如图，线段AB的两个端点坐标分别为A〔1，1〕，B〔2，1〕，以原点O 为位似中心，将线段AB放大后得到线段CD．假设CD=2，那么端点C的坐标为〔〕A.〔2，2〕B．〔2，4〕C．〔3，2〕D．〔4，2〕答案：A解析：解答：∵线段AB的两个端点坐标分别为A〔1，1〕，B〔2，1〕，∴AB=1，∵以原点O为位似中心，将线段AB放大后得到线段CD，CD=2，∴两图形位似比为：1；2，∴端点C的坐标为：〔2，2〕．应选；A.分析：利用A，B点坐标，得出AB=1，结合以O为位似中心，将线段AB放大后得到线段CD，CD=2，结合图形得出，那么点A的对应点C的坐标是A〔1，1〕的坐标同时乘以2，因而得到的点C的坐标．9. 将三角形三个顶点的横坐标都乘以2，纵坐标不变，那么所得三角形与原三角形的关系是〔〕A.将原图向左平移两个单位B．与原点对称C．纵向不变，横向拉长为原来的二倍D．关于y轴对称答案：C解析：解答：∵三角形三个顶点的横坐标都乘以2，纵坐标不变，∴纵向不变，横向拉长为原来的二倍．应选C．分析：三角形三个顶点的横坐标变化，纵坐标不变，即是图形纵向不变，横向变化．10. 以下说法中：①位似图形一定是相似图形；②相似图形一定是位似图形；③两个位似图形假设全等，那么位似中心在两个图形之间；④假设五边形ABCDE 与五边形A′B′C′D′E′位似，那么在五边形中连线组成的△ABC与△A′B′C′也是位似的．正确的个数是〔〕A.1 B．2 C．3 D．4答案：C解析：解答：利用位似的定义可知，位似图形一定是相似图形；但是相似图形不一定是位似图形，因为它是一种特殊的相似，所以①正确②错误，两个位似图形假设全等，根据对应点一定相交于一点，可得到位似中心在两个图形之间，③正确；④假设五边形ABCDE与五边形A′B′C′D′E′'位似，那么在五边形中连线组成的△ABC与△A′B′C′，画出图形，可得它也是位似．④正确．所以①③④正确．应选C．分析：利用位似图形的性质，各边之间的关系，以及对应点的关系可以解决．11. 如下图，正方形EFGH是由正方形ABCD经过位似变换得到的，点O是位似中心，E，F，G，H分别是OA，OB，OC，OD的中点，那么正方形EFGH与正方形ABCD的面积比是〔〕A.1：6 B．1：5 C．1：4 D．1：2答案：C解析：解答：∵正方形EFGH是由正方形ABCD经过位似变换得到的，点O 是位似中心，∴正方形EFGH∽正方形ABCD，∵E，F，G，H分别是OA，OB，OC，OD的中点，∴EH=12AD，即位似比为：EH：AD=1：2，∴正方形EFGH与正方形ABCD的面积比是：1：4．应选C．分析：由正方形EFGH是由正方形ABCD经过位似变换得到的，点O是位似中心，E，F，G，H分别是OA，OB，OC，OD的中点，易求得位似比等于EH：AD=1：2，又由相似三角形面积的比等于相似比的平方，即可求得正方形EFGH与正方形ABCD的面积比．12. 如图，菱形ABCD中，对角线AC、BD相交于点O，M、N分别是边AB、AD的中点，连接OM、ON、MN，那么以下表达正确的选项是〔〕A.△AOM和△AON都是等边三角形B．四边形MBON和四边形MODN都是菱形C．四边形AMON和四边形ABCD都是位似图形D．四边形MBCO和四边形NDCO都是等腰梯形答案：C解析：解答：根据位似图形的定义可知A．O与OM和AM的大小却无法判断，所以无法判断△AMO和△AON是等边三角形，故错误；B．无法判断BM是否等于OB和BM是否等于OC，所以也无法判断平行四边形MBON和MODN是菱形，故错误；C．四边形MBCO和四边形NDCO是位似图形，故此选项正确；D．无法判断四边形MBCO和NDCO是等腰梯形，故此选项错误；应选C．分析：在Rt△ABO中，根据直角三角形斜边上的中线等于斜边的一半可得，OM=AM=BM，但AO与OM和AM的大小却无法判断，所以无法判断△AMO和△AON 是等边三角形．同样，我们也无法判断BM是否等于OB和BM是否等于OC，所以也无法判断平行四边形MBON和MODN是菱形，也无法判断四边形MBCO和NDCO 是等腰梯形．根据位似图形的定义可知四边形MBCO和四边形NDCO是位似图形，故此题选C．13. 以下说法正确的选项是〔〕A.两个位似图形对应点连线有可能无交点B．两个位似图形对应点连线交点个数为1或2C．两个位似图形对应点连线只有一个交点D．两个位似图形对应点连线交点个数不少于4个答案：C解析：解答：A.两个位似图形对应点连线必有交点，故本选项错误；B.两个位似图形对应点连线只有1个交点，故本选项错误；C.只有一个交点正确，故本选项正确；D.交点只有1个，故本选项错误．应选C．分析：位似图形对应点连线必有交点，且交点只有1个．14. 用作位似形的方法，可以将一个图形放大或缩小，位似中心〔〕A.只能选在原图形的外部B．只能选在原图形的内部C．只能选在原图形的边上 D．可以选择任意位置答案：D解析：解答：位似中心可以选择任意位置．应选D．分析：用作位似形的方法，可以将一个图形放大或缩小，位似中心可以选择任意位置．15. 如图，四边形ABCD与四边形AEFG是位似图形，且AC：AF=2：3，那么以下结论不正确的选项是〔〕A.四边形ABCD与四边形AEFG是相似图形B．AD与AE的比是2：3C．四边形ABCD与四边形AEFG的周长比是2：3D．四边形ABCD与四边形AEFG的面积比是4：9答案：B解析：解答：∵四边形ABCD与四边形AEFG是位似图形；A.四边形ABCD与四边形AEFG一定是相似图形，故正确；B.AD与AG是对应边，故AD：AE=2：3；故错误；C.四边形ABCD与四边形AEFG的相似比是2：3，故正确；D.那么周长的比是2：3，面积的比是4：9，故正确．应选B．分析：此题主要考察了位似变换的定义及作图，位似变换就是特殊的相似，且位似图形上任意一对对应点到位似中心的距离之比等于相似比，因而周长的比等于相似比，面积的比等于相似比的平方．二、填空题16. 在直角坐标系中，△ABC的坐标分别是A〔-1，2〕，B〔-2，0〕，C〔-1，1〕，假设以原点O为位似中心，将△ABC放大到原来的2倍得到△A′B′C′，那么落在第四象限的A′的坐标是________答案：〔2，-4〕解析：解答：∵A〔-1，2〕，以原点O为位似中心，将△ABC放大到原来的2倍得到△A′B′C′，∴落在第四象限的A′的坐标是：〔2，-4〕．故答案为：〔2，-4〕．分析：根据位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k，即可得出A′的坐标．17. 在平面直角坐标系中，点A〔-4，2〕，B〔-2，-2〕，以原点O为位似中心，把△ABO放大为原来的2倍，那么点A的对应点A′的坐标是答案：〔-8，4〕或〔8，-4〕．解析：解答：∵点A的坐标分别为〔-4，2〕，以原点O为位似中心，把△ABO 放大为原来的2倍，那么A′的坐标是：〔-8，4〕或〔8，-4〕．故答案为：〔-8，4〕或〔8，-4〕．分析：根据在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k，即可求得答案．18. 如图，△ABC中，点D、E、F分别是AB、BC、AC的中点，那么与△ADF 位似的三角形是．答案：△ABC解析：解答：∵点D、E、F分别是AB、BC、AC的中点，∴DF∥BC，ED∥AC，EF∥AB，∴△ADF∽△ABC，那么△ADF与△ABC是位似图形．故答案为：△ABC．分析：利用三角形中位线定理以及位似变换的定义得出即可．19. 如图，点A〔0，1〕，B〔-2，0〕，以坐标原点O为位似中心，将线段AB 放大2倍，放大后的线段A′B′与线段AB在同一侧，那么两个端点A′，B′的坐标分别为答案：〔0，2〕〔-4，0〕．解析：解答：∵以坐标原点O为位似中心，将线段AB放大2倍，且点A〔0，1〕，B〔-2，0〕，∴两个端点A、B的对应点坐标分别为：〔0，2〕〔-4，0〕或〔0，-2〕〔4，0〕，∵放大后的线段A′B′与线段AB在同一侧，∴两个端点A′、B′的坐标分别为：〔0，2〕〔-4，0〕．故答案为：〔0，2〕〔-4，0〕．分析：由题意，根据位似图形的性质，即可求得两个端点A′，B′的坐标．20. 如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上．〔1〕△ABC的面积等于；〔2〕假设四边形DEFG是△ABC中所能包含的面积最大的正方形，请你在如下图的网格中，用直尺和三角尺画出该正方形，并简要说明画图方法〔不要求证明〕答案：6；．取格点P，连接PC，过点A画PC的平行线，与BC交于点Q，连接PQ与AC相交得点D，过点D画CB的平行线，与AB相交得点E，分别过点D、E画PC的平行线，与CB相交得点G，F，那么四边形DEFG即为所求．解析：解答：〔1〕△ABC的面积为：12×4×3=6；〔2〕如图，取格点P，连接PC，过点A画PC的平行线，与BC交于点Q，连接PQ与AC相交得点D，过点D画CB的平行线，与AB相交得点E，分别过点D、E画PC的平行线，与CB相交得点G，F，那么四边形DEFG即为所求．故答案为：〔Ⅰ〕6；〔Ⅱ〕取格点P，连接PC，过点A画PC的平行线，与BC交于点Q，连接PQ与AC相交得点D，过点D画CB的平行线，与AB相交得点E，分别过点D、E画PC的平行线，与CB相交得点G，F，那么四边形DEFG即为所求．分析：〔Ⅰ〕△ABC以AB为底，高为3个单位，求出面积即可；〔Ⅱ〕作出所求的正方形，如下图，画图方法为：取格点P，连接PC，过点A画PC的平行线，与BC交于点Q，连接PQ与AC相交得点D，过点D画CB的平行线，与AB相交得点E，分别过点D、E画PC的平行线，与CB相交得点G，F，那么四边形DEFG即为所求三、解答题21. 在平面直角坐标系中，△ABC的三个顶点坐标分别为A〔2，-4〕，B〔3，-2〕，C〔6，-3〕．〔1〕画出△ABC关于x轴对称的△A1B1C1；答案：解答：如下图：△A1B1C1，即为所求；〔2〕以M点为位似中心，在网格中画出△A1B1C1的位似图形△A2B2C2，使△A2B2C2与△A1B1C1的相似比为2：1．答案：解答：如下图：△A2B2C2，即为所求．解析：〔1〕利用轴对称图形的性质进而得出对应点位置进而画出图形即可；〔2〕利用位似图形的性质得出对应点位置进而画出图形即可．22. 点P为线段AB上一点，射线PM⊥AB，用直尺和圆规在PM上找一点C，使得PC2=AP•PB．答案：解答：如下图：作AB的垂直平分线，以O为圆心，12AB为半径作圆，射线PM交⊙O于点C，C点即为所求解析：利用垂径定理结合相似三角形的判定与性质得出C点即可．23. 如图，在平面直角坐标系中，△ABC的三个顶点坐标系分别为A〔-2，1〕，B〔-1，4〕，C〔-3，-2〕．〔1〕以原点O为位似中心，位似比为1：2，在y轴的左侧，画出△ABC放大后的图形△A1B1C1，并直接写出C1点坐标；答案：解答：〔1〕如下图：△A1B1C1即为所求，C1点坐标为〔-6，4〕；〔2〕如果点D〔a，b〕在线段AB上，请直接写出经过〔1〕的变化后点D 的对应点D1的坐标．答案：解答：如果点D〔a，b〕在线段AB上，经过〔1〕的变化后点D的对应点D1的坐标为；〔2a，2b〕．解析：〔1〕利用位似比为1：2，进而将各对应点坐标扩大为原来的2倍，进而得出答案；〔2〕利用〔1〕中位似比得出对应点坐标关系．24. 如图，在平面直角坐标系中，四边形OABC的顶点坐标分别是O〔0，0〕，A〔3，0〕，B〔4，4〕，C〔-2，3〕，将点O，A，B，C的横坐标、纵坐标都乘以-2．〔1〕画出以变化后的四个点为顶点的四边形；答案：解答：如下图，四边形OA′B′C′即为所求四边形；〔2〕由〔1〕得到的四边形与四边形OABC位似吗？如果位似，指出位似中心及与原图形的相似比．答案：解答：∵将点O，A，B，C的横坐标、纵坐标都乘以-2可得出四边形OA′B′C′，∴各对应边的比为2，对应点的连线都过原点，∴得到的四边形与四边形OABC位似，位似中心是O〔0，0〕，与原图形的相似比为2．解析：〔1〕将点O，A，B，C的横坐标、纵坐标都乘以-2得O〔0，0〕，A′〔-6，0〕，B′〔-8，-8〕，C′〔4，-6〕，顺次连接各点即可；1 〔2〕根据位似图形的定义可知得到的四边形与四边形OABC位似，根据图形可得出位似中心及位似比．25. 如下图，图中的小方格都是边长为1的正方形，△ABC与△A′B′C′是以点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上．〔1〕画出位似中心点O；答案：解答：图中点O为所求；〔2〕直接写出△ABC与△A′B′C′的位似比；答案：解答：△ABC与△A′B′C′的位似比等于2：1；〔3〕以位似中心O为坐标原点，以格线所在直线为坐标轴建立平面直角坐标系，画出△A′B′C′关于点O中心对称的△A″B″C″，并直接写出△A″B″C″各顶点的坐标．答案：解答：△A″B″C″为所求；A″〔6，0〕；B″〔3，-2〕；C″〔4，-4〕．解析：〔1〕连接CC′并延长，连接BB′并延长，两延长线交于点O；〔2〕由OB=2OB′，即可得出△ABC与△A′B′C′的位似比为2：1；〔3〕，连接B′O并延长，使OB″=OB′，延长A′O并延长，使OA″=OA′，C′O并延长，使OC″=OC′，连接A″B″，A″C″，B″C″，那么△A″B″C″为所求，从网格中即可得出△A″B″C″各顶点的坐标．。

华师大新版九年级上学期《23.5 位似图形》同步练习卷一．选择题（共5小题）1．在平面直角坐标系中，△OAB各顶点的坐标分别为：O（0，0），A（1，2），B（0，3），以O为位似中心，△OA′B′与△OAB位似，若B点的对应点B′的坐标为（0，﹣6），则A点的对应点A′坐标为（）A．（﹣2，﹣4）B．（﹣4，﹣2）C．（﹣1，﹣4）D．（1，﹣4）2．如图所示，在平面直角坐标系中，已知点A（2，4），过点A作AB⊥x轴于点B．将△AOB以坐标原点O为位似中心缩小为原图形的，得到△COD，则CD 的长度是（）A．2B．1C．4D．23．在平面直角坐标系中，点P（m，n）是线段AB上一点，以原点O为位似中心把△AOB放大到原来的两倍，则点P的对应点的坐标为（）A．（2m，2n）B．（2m，2n）或（﹣2m，﹣2n）C．（m，n）D．（m，n）或（﹣m，﹣n）4．在平面直角坐标系中，线段AB两个端点的坐标分别为A（6，8），B（10，2），若以原点O为位似中心，在第一象限内将线段AB缩短为原来的后得到线段CD，则点A的对应点C的坐标为（）A．（5，1）B．（4，3）C．（3，4）D．（1，5）5．如图，矩形EFGO的两边在坐标轴上，点O为平面直角坐标系的原点，以y轴上的某一点为位似中心，作位似图形ABCD，且点B，F的坐标分别为（﹣4，4），（2，1），则位似中心的坐标为（）A．（0，3）B．（0，2.5）C．（0，2）D．（0，1.5）二．填空题（共5小题）6．如图，已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形，且=，若点A（﹣1，0），点C（，1），则A′C′=．7．如图，在平面直角坐标系中，每个小方格都是边长为1个单位长度的正方形，已知△AOB与△A1OB1位似，位似中心为原点O，且相似比为3：2，点A，B 都在格点上，则点B1的坐标为．8．如图，四边形ABCD与四边形EFGH位似，其位似中心为点O，且=，则=．9．如图，△AOB三个顶点的坐标分别为A（8，0），O（0，0），B（8，﹣6），点M为OB的中点．以点O为位似中心，把△AOB缩小为原来的，得到△A′O′B′，点M′为O′B′的中点，则MM′的长为．10．如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为3：4，∠OCD=90°，∠AOB=60°，若点B的坐标是（6，0），则点C的坐标是．三．解答题（共40小题）11．在如图所示的平面直角坐标系中，已知点A（﹣3，﹣3），点B（﹣1，﹣3），点C（﹣1，﹣1）．（1）画出△ABC；（2）画出△ABC关于x轴对称的△A1B1C1，并写出A1点的坐标：；（3）以O为位似中心，在第一象限内把△ABC扩大到原来的两倍，得到△A2B2C2，并写出A2点的坐标：．12．已知：△ABC三个顶点的坐标分别为A（﹣2，﹣2），B（﹣5，﹣4），C（﹣1，﹣5）．（1）画出△ABC关于x轴对称的△A1B1C1；（2）以点O为位似中心，将△ABC放大为原来的2倍，得到△A2B2C2，请在网格中画出△A2B2C2，并写出点B2的坐标．13．如图，△ABC中，A（﹣4，4），B（﹣4，﹣2），C（﹣2，2）．（1）请画出将△ABC向右平移8个单位长度后的△A1B l C1；（2）求出∠A1B l C1的余弦值；（3）以O为位似中心，将△A1B l C1缩小为原来的，得到△A2B2C2，请在y轴右侧画出△A2B2C2．14．如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点都在格点上．（1）在所给的网格中画出与△ABC相似（相似比不为1）的△A1B1C1（画出一个即可）；（2）在所给的网格中，将△ABC绕点C顺时针旋转90°得到△A2B2C，画出△A2B2C，并直接写出在此旋转过程中点A经过的路径长．15．如图，在由边长为1个单位长度的小正方形组成的网格中，给出了两个格点△ABC和△DEF（顶点在网格线的交点上）．（1）平移△ABC，使得△ABC和△DEF组成一个轴对称图形，在网格中画出这个轴对称图形；（2）在网格中画一个格点△A′B′C′，使△A′B′C′∽△ABC，且相似比不为1．16．如图，在由边长为1个单位长度的小正方形组成的12×2网格中，给出了格点△ABC和直线l．（1）画出△ABC关于直线l对称的格点△A′B′C；（2）在直线l上选取一格点，在网格内画出格点△DPE，使得△DPE∽△ABC，且相似比为2：1．17．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC （顶点网格线的交点）以及格点P．（1）将△ABC绕点P逆时针旋转90°得到△DEF，画出△DEF；（2）以D为一个顶点，画一个格点△A1B1C1，使得△A1B1C1∽△ABC，且相似比为2．18．已知，如图，△ABC中，AB=2，BC=4，D为BC边上一点，BD=1．（1）求证：△ABD∽△CBA；（2）在原图上作DE∥AB交AC与点E，请直接写出另一个与△ABD相似的三角形，并求出DE的长．19．如图所示，在边长为1个单位长度的小正方形组成的网格中，△ABC是格点三角形（三角形的顶点是网格线的交点）．（1）画一个格点△DEF，使△DEF与△ABC相似；（2）运用所学知识证明△DEF与△ABC相似．20．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC （顶点是网格线的交点）．（1）将△ABC向上平移3个单位得到△A1B1C1，请画出△A1B1C1；（2）请画一个格点△A2B2C2，使△A2B2C2∽△ABC，且相似比为2．、21．方格纸中每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．（1）在10×10的方格中（每个小方格的边长为1个单位），画一个面积为2的格点钝角三角形ABC，并标明相应字母；（2）再在方格中画一个格点△DEF，使得△DEF∽△ABC，且面积之比为2：1，并加以证明．22．已知：如图，△ABC的顶点坐标分别是A（﹣2，3），B（﹣3，2），C（﹣1，1）．（1）以点C为位似中心，位似比为2，将△ABC放大得到△A1B1C1，在网格内画出△A1B1C1；（2）将△ABC绕点O顺时针旋转90°得到△A2B2C2，画出△A2B2C2，并写出点B 的对应点B2的坐标．23．已知O是坐标原点，A、B的坐标分别为（3，1）、（2，﹣1）（1）画出△OAB绕点O顺时针旋转90°后得到的△OA1B1；（2）在y轴的左侧以O为位似中心作△OAB的位似△OA2B2（要求：新图与原图的相似比为2：1）．24．如图，△ABC与△A1B1C1是位似图形．在网格上建立平面直角坐标系，使得点A的坐标为（1，﹣6）．（1）在图上标出点，△ABC与△A1B1C1的位似中心P．并写出点P的坐标为；（2）以点A为位似中心，在网格图中作△AB2C2，使△AB2C2和△ABC位似，且位似比为1：2，并写出点C2的坐标为．25．如图，在9×9网格中，每个小方格的边长看作单位1，每个小方格的顶点叫作格点，△ABC的顶点都在格点上．（1）请在网格中画出△ABC的一个位似图形△A1B1C，使两个图形以点C为位似中心，且所画图形与△ABC的相似比为2：1；（2）将△A1B1C绕着点C顺时针旋转90°得△A2B2C，画出图形，并在如图所示的坐标系中分别写出△A2B2C三个顶点的坐标．26．如图，在由边长为1个单位长度的小正方形组成的10×10网格中，已知点O，A，B均为网格线的交点．（1）在给定的网格中，以点O为位似中心，将线段AB放大为原来的2倍，得到线段A1B1（点A，B的对应点分别为A1，B1），画出线段A1B1；（2）将线段A1B1绕点B1逆时针旋转90°得到线段A2B1，画出线段A2B1；（3）以A，A1，B1，A2为顶点的四边形AA1B1A2的面积是个平方单位．27．如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，﹣4）．（1）请在图中，画出△ABC向左平移6个单位长度后得到的△A1B1C1；（2）以点O为位似中心，将△ABC缩小为原来的，得到△A2B2C2，请在图中y 轴右侧，画出△A2B2C2，并求出∠A2B2C2的正弦值．28．画图，将图中的△ABC作下列运动，画出相应的图形．（1）在图（1）上，沿y轴正方向平移2个单位；（2）在图（2）上，关于y轴对称；（3）在图（3）上，以B点为位似中心，放大到2倍．29．如图，在直角坐标系中△ABC的A．B．C三点坐标为A（7，1）、B（8，2）、C（9，0）．（1）请在图中画出△ABC的一个以点P（12，0）为位似中心，相似比为3的位似图形△A′B′C′（要求与△ABC同在P点一侧），再画出△A′B′C′关于y轴对称的△A″B″C″；（2）写出A′的坐标．30．如图，在直角坐标系中△ABC的A、B、C三点坐标为A（7，1）、B（8，2）、C（9，0）．（1）请在图中画出△ABC的一个以点P（12，0）为位似中心，相似比为3的位似图形△A′B′C′（要求与△ABC同在P点一侧），画出△A′B′C′关于y轴对称的△A′'B′'C′'；（2）写出点A'的坐标．31．如图，在边长为1个单位长度的小正方形组成的12×12网格中建立平面直角坐标系，格点△ABC（顶点是网格线的交点）的坐标分别是A（﹣2，2），B （﹣3，1），C（﹣1，0）．（1）将△ABC绕点O逆时针旋转90°得到△DEF，画出△DEF；（2）以O为位似中心，将△ABC放大为原来的2倍，在网格内画出放大后的△A1B1C1，若P（x，y）为△ABC中的任意一点，这次变换后的对应点P1的坐标为（，）32．在12×12的网格中，每个小正方形的边长均为1，建立如图所示的平面直角坐标系，按照要求作图并解答相关问题．（1）将△ABC围绕这原点O按顺时针方向旋转90°，得到△A1B1C1；（2）以坐标原点O为位似中心，作出与△A1B1C1位似且位似比为1：2的△A2B2C2，并写出点A2的坐标．33．如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，﹣4）．（1）请在图中，画出△ABC向左平移6个单位长度后得到的△A1B1C1；（2）以点O为位似中心，将△ABC缩小为原来的，得到△A2B2C2，请在图中y 轴右侧，画出△A2B2C2，并写出C2的坐标．34．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B （﹣1，4），C（﹣3，2）（1）画出△ABC关于点B成中心对称的图形△A1BC1；（2）以原点O为位似中心，位似比为1：2，在y轴的左侧画出△ABC放大后的图形△A2B2C2，并直接写出C2的坐标．35．如图，图中的小方格是边长为1的正方形，△ABC与△A’B’C’是关于点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上．（1）画出位似中心点O；（2）求出△ABC与△A′B′C′的位似比；（3）以点O为位似中心，在图中画一个△A2B2C2，使它与△ABC的位似比等于3：2．36．已知，△ABC在直角坐标平面内，三个顶点的坐标分别是A（0，3）、B（3，4）、C（2，2），正方形网格中，每个小正方形的边长是一个单位长度．（1）画出△ABC向左平移4个单位长度得到的△A1B1C1，点C1的坐标是；（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是；（画出图形）（3）△A2B2C2的面积是平方单位．37．在平面直角坐标系中，点A、B的坐标分别是（0，3）、（﹣4，0），（1）将△AOB绕点A逆时针旋转90°得到△AEF，点O，B对应点分别是E，F，请在图中画出△AEF，并写出E、F的坐标；（2）以O点为位似中心，将△AEF作位似变换且缩小为原来的，在网格内画出一个符合条件的△A1E1F1．38．已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．（1）画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是；（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是．39．如图，在边长为1个单位长度的小正方形组成的网格中．（1）以图中的点O为位似中心，在网格中画出△ABC的位似图形△A1B1C1，使△A1B1C1与△ABC的位似比为2：1；（2）若△A1B1C1的面积为S，则△ABC的面积是．40．如图，△ABC的顶点坐标分别为A（1，3）、B（4，2）、C（2，1）．（1）作出与△ABC关于x轴对称的△A 1B1C1，并写出点A1的坐标；（2）以原点O 为位似中心，在原点的另一侧画出△A2B2C2，使=，并写出点A2的坐标．41．如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点都在格点上，建立如图所示的平面直角坐标系．（1）将△ABC向左平移7个单位后再向下平移3个单位，请画出两次平移后的△A1B1C1，若M为△ABC内的一点，其坐标为（a，b），直接写出两次平移后点M的对应点M1的坐标；（2）以原点O为位似中心，将△ABC缩小，使变换后得到的△A2B2C2与△ABC对应边的比为1：2．请在网格内画出在第三象限内的△A2B2C2，并写出点A2的坐标．42．如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A1B1C1和△A2B2C2；（1）把△ABC绕点O顺时针旋转90°得到△A1B1C1；（2）以图中的O为位似中心，在△A1B1C1的同侧将△A1B1C1作位似变换且放大到原来的两倍，得到△A2B2C2．43．如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（﹣1，2），B（﹣3，4），C（﹣2，6）．（1）画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1；（2）以原点O为位似中心，在图中画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2，并写出A2、B2、C2的坐标．44．如图在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC、直线l和格点O．（1）画出△ABC关于直线l成轴对称的△A0B0C0；（2）画出将△A0B0C0向上平移1个单位得到的△A1B1C1；（3）以格点O为位似中心，将△A1B1C1作位似变换，将其放大到原来的两倍，得到△A2B2C2．45．已知：如图，△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．（1）以点B为位似中心，在网格内画出△A1B1C1，使△A1B1C1与△ABC位似，且位似比为2：1，点C1的坐标是；（2）△A1B1C1的面积是平方单位．46．如图，在10×10网格中，每个小方格的边长看做单位1，每个小方格的顶点叫做格点，△ABC的顶点都在格点上．（1）请在网格中画出△ABC的一个位似图形△A1B1C1，使两个图形以点C为位似中心，且所画图形与△ABC的位似比为2：1；（2）将△A1B1C1绕着点C1顺时针旋转90°得△A2B2C2，画出图形，并分别写出△A2B2C2三个顶点的坐标．47．在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，3），B（﹣4，0），C（1，1）（1）以M点为位似中心，在点M的同侧作△ABC关于M点的位似图形△A1B1C1，使△A1B1C1与△ABC的位似比为2：1；（2）请直接写出A1、B1、C1三点的坐标．48．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC （顶点是网格线的交点）和格点P．（1）以A点为位似中心，将△ABC在网格中放大成△AB1C1，使，请画出△AB1C1；（2）以P点为三角形的一个顶点，请画一个格点△PMN，使△PMN∽△ABC，且相似比为．49．如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了直线l和格点△ABC（顶点是网格线的交点）（1）将△ABC向左平移6个单位，再向下平移5单位，请画出平移后的△A1B1C1；（2）以点O为位似中心，将△ABC缩小为原来的，得到△A2B2C2，请在直线l 右侧画出△A2B2C2，并求出A2O的长度．50．如图，在边长为1个单位长度的小正方形组成的网格中，建立了平面直角坐标系，给出了格点△ABC和△DEF（顶点是网格线的交点）以及格点P（3，8）．（1）将△ABC怎样旋转能得到△DEF？指出旋转的方向、角度及旋转中心的坐标；（2）以P（3，8）点为位似中心，将△ABC作位似变换，且放大到原来的2倍，得到△A1B1C1，画出△A1B1C1．华师大新版九年级上学期《23.5 位似图形》同步练习卷参考答案与试题解析一．选择题（共5小题）1．在平面直角坐标系中，△OAB各顶点的坐标分别为：O（0，0），A（1，2），B（0，3），以O为位似中心，△OA′B′与△OAB位似，若B点的对应点B′的坐标为（0，﹣6），则A点的对应点A′坐标为（）A．（﹣2，﹣4）B．（﹣4，﹣2）C．（﹣1，﹣4）D．（1，﹣4）【分析】利用已知对应点的坐标变化规律得出位似比为1：2，则可求A'坐标．【解答】解：∵△OA′B′与△OAB关于O（0，0）成位似图形，且若B （0，3）的对应点B′的坐标为（0，﹣6），∴OB：OB'=1：2=OA：OA'∵A（1，2），∴A'（﹣2，﹣4）故选：A．【点评】此题主要考查了位似变换与坐标与图形的性质，得出位似比是解题关键2．如图所示，在平面直角坐标系中，已知点A（2，4），过点A作AB⊥x轴于点B．将△AOB以坐标原点O为位似中心缩小为原图形的，得到△COD，则CD 的长度是（）A．2B．1C．4D．2【分析】直接利用位似图形的性质以及结合A点坐标直接得出点C的坐标，即可得出答案．【解答】解：∵点A（2，4），过点A作AB⊥x轴于点B．将△AOB以坐标原点O 为位似中心缩小为原图形的，得到△COD，∴C（1，2），则CD的长度是：2．故选：A．【点评】此题主要考查了位似变换以及坐标与图形的性质，正确把握位似图形的性质是解题关键．3．在平面直角坐标系中，点P（m，n）是线段AB上一点，以原点O为位似中心把△AOB放大到原来的两倍，则点P的对应点的坐标为（）A．（2m，2n）B．（2m，2n）或（﹣2m，﹣2n）C．（m，n）D．（m，n）或（﹣m，﹣n）【分析】根据位似变换的性质计算即可．【解答】解：点P（m，n）是线段AB上一点，以原点O为位似中心把△AOB放大到原来的两倍，则点P的对应点的坐标为（m×2，n×2）或（m×（﹣2），n×（﹣2）），即（2m，2n）或（﹣2m，﹣2n），故选：B．【点评】本题考查的是位似变换、坐标与图形的性质，在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k．4．在平面直角坐标系中，线段AB两个端点的坐标分别为A（6，8），B（10，2），若以原点O为位似中心，在第一象限内将线段AB缩短为原来的后得到线段CD，则点A的对应点C的坐标为（）A．（5，1）B．（4，3）C．（3，4）D．（1，5）【分析】利用位似图形的性质，结合两图形的位似比进而得出C点坐标．【解答】解：∵以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，∴端点C的横坐标和纵坐标都变为A点的横坐标和纵坐标的一半，又∵A（6，8），∴端点C的坐标为（3，4）．故选：C．【点评】此题主要考查了位似图形的性质，利用两图形的位似比得出对应点横纵坐标关系是解题关键．5．如图，矩形EFGO的两边在坐标轴上，点O为平面直角坐标系的原点，以y 轴上的某一点为位似中心，作位似图形ABCD，且点B，F的坐标分别为（﹣4，4），（2，1），则位似中心的坐标为（）A．（0，3）B．（0，2.5）C．（0，2）D．（0，1.5）【分析】连接BF交y轴于P，根据题意求出CG，根据相似三角形的性质求出GP，求出点P的坐标．【解答】解：如图，连接BF交y轴于P，∵四边形ABCD和四边形EFGO是矩形，点B，F的坐标分别为（﹣4，4），（2，1），∴点C的坐标为（0，4），点G的坐标为（0，1），∴CG=3，∵BC∥GF，∴==，∴GP=1，PC=2，∴点P的坐标为（0，2），故选：C．【点评】本题考查的是位似变换的概念、坐标与图形性质，掌握如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心是解题的关键．二．填空题（共5小题）6．如图，已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形，且=，若点A（﹣1，0），点C（，1），则A′C′=．【分析】根据位似图形的性质和已知求出C′D和OA′，求出A′D，根据勾股定理求出A′C′即可．【解答】解：设C′作C′D′⊥x轴于D，∵△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形，且=，点A （﹣1，0），点C（，1），∴A′（﹣2，0），C′（1，2），∴OA′=2，DC′=2，OD=1，∴A′D=1+2=3，∴A′C′==，故答案为：．【点评】本题考查了位似变换、坐标与图形性质、勾股定理等知识点，能求出点A′和C′的坐标是解此题的关键．7．如图，在平面直角坐标系中，每个小方格都是边长为1个单位长度的正方形，已知△AOB与△A1OB1位似，位似中心为原点O，且相似比为3：2，点A，B 都在格点上，则点B1的坐标为（﹣2，﹣）．【分析】把B的横纵坐标分别乘以﹣得到B′的坐标．【解答】解：由题意得：△AOB与△A1OB1位似，位似中心为原点O，且相似比为3：2，又∵B（3，1）∴B′的坐标是[3×（﹣），1×（﹣）]，即B′的坐标是（﹣2，﹣）；故答案为：（﹣2，﹣）．【点评】本题考查了位似变换：先确定点的坐标，及相似比，再分别把横纵坐标与相似比相乘即可，注意原图形与位似图形是同侧还是异侧，来确定所乘以的相似比的正负．8．如图，四边形ABCD与四边形EFGH位似，其位似中心为点O，且=，则=．【分析】直接利用位似图形的性质结合位似比等于相似比得出答案．【解答】解：∵四边形ABCD与四边形EFGH位似，其位似中心为点O，且=，∴=，则==．故答案为：．【点评】此题主要考查了位似变换，正确掌握位似图形的性质是解题关键．9．如图，△AOB三个顶点的坐标分别为A（8，0），O（0，0），B（8，﹣6），点M为OB的中点．以点O为位似中心，把△AOB缩小为原来的，得到△A′O′B′，点M′为O′B′的中点，则MM′的长为或．【分析】分两种情形画出图形，即可解决问题；【解答】解：如图，在Rt△AOB中，OB==10，①当△A′OB′在第四象限时，MM′=．②当△A″OB″在第二象限时，MM′=，故答案为或．【点评】本题考查位似变换，坐标与图形的性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．10．如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为3：4，∠OCD=90°，∠AOB=60°，若点B的坐标是（6，0），则点C的坐标是（2，2）．【分析】根据题意得出D点坐标，再解直角三角形进而得出答案．【解答】解：分别过A、C作AE⊥OB，CF⊥OB，∵∠OCD=90°，∠AOB=60°，∴∠ABO=∠CDO=30°，∠OCF=30°，∵△OAB与△OCD是以点O为位似中心的位似图形，相似比为3：4，点B的坐标是（6，0），∴D（8，0），则DO=8，故OC=4，则FO=2，CF=CO•cos30°=4×=2，故点C的坐标是：（2，2）．故答案为：（2，2）．【点评】此题主要考查了位似变换，运用位似图形的性质正确解直角三角形是解题关键．三．解答题（共40小题）11．在如图所示的平面直角坐标系中，已知点A（﹣3，﹣3），点B（﹣1，﹣3），点C（﹣1，﹣1）．（1）画出△ABC；（2）画出△ABC关于x轴对称的△A1B1C1，并写出A1点的坐标：（﹣3，3）；（3）以O为位似中心，在第一象限内把△ABC扩大到原来的两倍，得到△A2B2C2，并写出A2点的坐标：（6，6）．【分析】（1）根据A、B、C三点坐标画出图形即可；（2）作出A、B、C关于轴的对称点A1、B1、C1即可；（3）延长OC到C2，使得OC2=2OC，同法作出A2，B2即可；【解答】解：（1）△ABC如图所示；（2）△A1B1C1如图所示；A1（﹣3，3），（3）△A2B2C2如图所示；A2（6，6）．故答案为（﹣3，3），（6，6）．【点评】本题考查作图﹣位似变换，轴对称变换等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．12．已知：△ABC三个顶点的坐标分别为A（﹣2，﹣2），B（﹣5，﹣4），C（﹣1，﹣5）．（1）画出△ABC关于x轴对称的△A1B1C1；（2）以点O为位似中心，将△ABC放大为原来的2倍，得到△A2B2C2，请在网格中画出△A2B2C2，并写出点B2的坐标．【分析】（1）利用关于y轴对称点的性质得出对应点得出即可；（2）利用位似图形的性质得出对应点坐标进而得出答案．【解答】解：（1）如图所示：△A1B1C1即为所求：（2）如图所示：△A2B2C2即为所求；B2（10，8）【点评】此题主要考查了位似变换与轴对称变换，得出对应点位置是解题关键．13．如图，△ABC中，A（﹣4，4），B（﹣4，﹣2），C（﹣2，2）．（1）请画出将△ABC向右平移8个单位长度后的△A1B l C1；（2）求出∠A1B l C1的余弦值；（3）以O为位似中心，将△A1B l C1缩小为原来的，得到△A2B2C2，请在y轴右侧画出△A2B2C2．【分析】（1）直接利用平移的性质得出对应点位置进而得出答案；（2）直接利用余弦的定义结合勾股定理得出答案；（3）利用位似图形的性质得出对应点位置进而得出答案．【解答】解：（1）如图所示：△A1B l C1，即为所求；（2）∠A1B l C1的余弦值为：==；（3）如图所示：△A2B2C2，即为所求．【点评】此题主要考查了位似变换以及平移变换和解直角三角形，正确得出对应点位置是解题关键．14．如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点都在格点上．（1）在所给的网格中画出与△ABC相似（相似比不为1）的△A1B1C1（画出一个即可）；（2）在所给的网格中，将△ABC绕点C顺时针旋转90°得到△A2B2C，画出△A2B2C，并直接写出在此旋转过程中点A经过的路径长．【分析】（1）直接利用相似图形的性质得出符合题意的图形；（2）直接利用旋转的性质得出对应点位置进而得出答案，再利用弧长公式计算得出答案．【解答】解：（1）如图所示：△A1B1C1，即为所求；（2）如图所示：△A2B2C，即为所求，点A经过的路径长为：=π．【点评】此题主要考查了相似变换以及旋转变换，正确得出对应点位置是解题关键．15．如图，在由边长为1个单位长度的小正方形组成的网格中，给出了两个格点△ABC和△DEF（顶点在网格线的交点上）．（1）平移△ABC，使得△ABC和△DEF组成一个轴对称图形，在网格中画出这个轴对称图形；（2）在网格中画一个格点△A′B′C′，使△A′B′C′∽△ABC，且相似比不为1．【分析】（1）平移△ABC，速度AB与DE重合即可；（2）画出相似比为1：2D的△A′B′C′即可；【解答】解：（1）如图（答案不唯一）．（2）如图（答案不唯一）．【点评】本题考查作图﹣相似变换，轴对称等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．16．如图，在由边长为1个单位长度的小正方形组成的12×2网格中，给出了格点△ABC和直线l．（1）画出△ABC关于直线l对称的格点△A′B′C；（2）在直线l上选取一格点，在网格内画出格点△DPE，使得△DPE∽△ABC，且相似比为2：1．【分析】（1）直接利用关于l对称点的性质得出答案；（2）直接利用相似图形的性质得出对应点位置进而得出答案．【解答】解：（1）如图所示：△A′B′C′即为所求；（2）如图所示：△DPE即为所求．【点评】此题主要考查了相似变换以及对称变换，正确得出对应点位置是解题关键．17．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC （顶点网格线的交点）以及格点P．（1）将△ABC绕点P逆时针旋转90°得到△DEF，画出△DEF；（2）以D为一个顶点，画一个格点△A1B1C1，使得△A1B1C1∽△ABC，且相似比为2．【分析】（1）直接利用旋转对称图形的性质得出对应点位置进而得出答案；（2）利用相似图形的性质，结合D点位置得出对应点位置进而得出答案．【解答】解：（1）如图所示：△DEF，即为所求；（2）如图所示：△A1B1C1，即为所求．【点评】此题主要考查了旋转变换以及相似变换，正确得出对应点位置是解题关键．18．已知，如图，△ABC中，AB=2，BC=4，D为BC边上一点，BD=1．（1）求证：△ABD∽△CBA；（2）在原图上作DE∥AB交AC与点E，请直接写出另一个与△ABD相似的三角形，并求出DE的长．【分析】（1）在△ABD与△CBA中，有∠B=∠B，根据已知边的条件，只需证明夹此角的两边对应成比例即可；（2）由（1）知△ABD∽△CBA，又DE∥AB，易证△CDE∽△CBA，则：△ABD∽△CDE，然后根据相似三角形的对应边成比例得出DE的长．【解答】（1）证明：∵AB=2，BC=4，BD=1，∴==，=，∴=，∵∠ABD=∠CBA，∴△ABD∽△CBA；（2）解：∵DE∥AB，∴△CDE∽△CBA，∴△ABD∽△CDE，∴DE=1.5．【点评】本题主要考查了相似三角形的判定及性质．平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；两组对应边的比相等且相应的夹角相等的两个三角形相似；相似三角形的对应边成比例．19．如图所示，在边长为1个单位长度的小正方形组成的网格中，△ABC是格点三角形（三角形的顶点是网格线的交点）．（1）画一个格点△DEF，使△DEF与△ABC相似；（2）运用所学知识证明△DEF与△ABC相似．【分析】（1）将△ABC的三边扩大相同的倍数，即可得到△DEF；（2）依据勾股定理求得三角形的边长，根据三边对应成比例的三角形相似，即可得到△DEF与△ABC相似．【解答】解：（1）如图所示，△DEF即为所求；（2）证明：由勾股定理可得，AB=，AC=，DE=2，DF=2，又∵BC=2，EF=4，∴===，∴△ABC∽△DEF．【点评】本题主要考查了利用相似变换进行作图，解决问题的关键是掌握：三边对应成比例的三角形相似．20．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC （顶点是网格线的交点）．（1）将△ABC向上平移3个单位得到△A1B1C1，请画出△A1B1C1；（2）请画一个格点△A2B2C2，使△A2B2C2∽△ABC，且相似比为2．、【分析】（1）直接利用平移的性质得出对应点位置进而得出答案；（2）直接利用相似图形的性质得出符合题意的答案．【解答】解：（1）如图所示：△A1B1C1即为所求；（2）如图所示：△A2B2C2即为所求．【点评】此题主要考查了平移变换以及相似变换，正确得出对应点位置是解题关键．21．方格纸中每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．（1）在10×10的方格中（每个小方格的边长为1个单位），画一个面积为2的格点钝角三角形ABC，并标明相应字母；（2）再在方格中画一个格点△DEF，使得△DEF∽△ABC，且面积之比为2：1，。

23.5位似图形 同步练习一、选择题1. 下列说法不正确的是 （ ） A ．位似图形一定是相似图形 B. 相似图形不一定是位似图形C. 位似图形上任意一对对应点到位似中心的距离之比等于位似比D. 位似图形中每组对应点所在的直线必相互平行2、如图，线段CD 两个端点的坐标分别为C （1，2）、D （2，0），以原点为位似中心，将线段CD 放大得到线段AB ， 若点B 坐标为（5，0），则点A 的坐标为（ ）A 、（2，5）B 、（2.5，5）C 、（3，5）D 、（3，6）3． 如图，点D E F ，，分别是()ABC AB AC >△各边的中点，下列说法中，错误．．的是（ ） A. AD 平分BAC ∠ B.12EF BC=C. EF 与AD 互相平分D.△DEF 是△ABC 的位似图形4、如图，△ABC 经过位似变换得到△DEF ， 点O 是位似中心且OA=AD ， 则△ABC 与△DEF 的面积比是（ ）A 、1：6B 、1：5C 、1：4D 、1：25、 将一个菱形放在2倍的放大镜下，则下列说法中不正确的是 （ ）ABDEFC第3题A ．菱形的边长扩大到原来的2倍B ．菱形的角的度数不变C ．菱形的面积扩大到原来的2倍D ．菱形的面积扩大到原来的4倍6、如图，△DEF 与△ABC 是位似图形，点O 是位似中心，D 、E 、F 分别是OA 、OB 、OC 的中点，则△DEF 与△ABC 的面积比是（ ）A 、1：6B 、1：5C 、1：4D 、1：27、 如图，已知BC ∥DE ，则下列说法中不正确的是 （ ） A ．两个三角形是位似图形 B ．点A 是两个三角形的位似中心 C ．AE ︰AD 是位似比 D ．点B 与点E 、点C 与点D 是对应位似点8、如图，线段AB 的两个端点坐标分别为A （1，1），B （2，1），以原点O 为位似中心，将线段AB 放大后得到线段CD.若CD=2，则端点C 的坐标为（ ）A 、（2，2）B 、（2，4）C 、（3，2）D 、（4，2）9、 已知△ABC ，以点A 为位似中心，作出△ADE ，使△ADE 是△ABC 放大2倍的图形，这样的图形可以作出 个（ ）A ．1个B ．2个C ．4个D ．无数个10、下列说法中：①位似图形一定是相似图形；②相似图形一定是位似图形；③两个位似图形若全等，则位似中心在两个图形之间；④若五边形ABCDE 与五边形A′B′C′D′E′位似，则在五边形中连线组成的△ABC 与△A′B′C′也是位似的.正确的个数是（ ）A 、1B 、2C 、3ABC DE 第7题D 、411、如图所示，正方形EFGH 是由正方形ABCD 经过位似变换得到的，点O 是位似中心，E ， F ， G ， H 分别是OA ， OB ， OC ， OD 的中点，则正方形EFGH 与正方形ABCD 的面积比是（ ）A 、1：6B 、1：5C 、1：4D 、1：212、 如图，以A 为位似中心，将△ADE 放大2倍后，得位似图形△AB C ，若 1S 表示△ADE 的面积，2S 表示四边形DBCE 的面积，则21:S S = （ ）A ． 1︰2B ．1︰3C ．1︰4D ．2︰3 13、下列说法正确的是（ ） A 、两个位似图形对应点连线有可能无交点 B 、两个位似图形对应点连线交点个数为1或2 C 、两个位似图形对应点连线只有一个交点 D 、两个位似图形对应点连线交点个数不少于4个14、用作位似形的方法，可以将一个图形放大或缩小，位似中心（ ） A 、只能选在原图形的外部 B 、只能选在原图形的内部C 、只能选在原图形的边上D 、可以选择任意位置ABD E 第1215、如图，四边形ABCD与四边形AEFG是位似图形，且AC：AF=2：3，则下列结论不正确的是（）A、四边形ABCD与四边形AEFG是相似图形B、AD与AE的比是2：3C、四边形ABCD与四边形AEFG的周长比是2：3D、四边形ABCD与四边形AEFG的面积比是4：9二、填空题16、把一个正多边形放大到原来的2.5倍，则原图与新图的相似比为________．17、如果两个位似图形的对应线段长分别为3cm和5cm，且较小图形周长为30cm，则较大图形周长为 .18、△ABC中，点D、E、F分别是AB、BC、AC的中点，则与△ADF位似的三角形是________.19、雨后操场，小明从他前面2米远的一小块积水中看到了旗杆顶端的倒影，如果旗杆底端到积水的距离为20米，小明眼睛离地面1.5米，则旗杆的高度为．20、将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上，ABC的面积等于________；三、综合题21、如图，已知△ABC 中，AB =12，BC =8，AC =6，点D 、E 分别在AB 、AC 上，如果以A 、D 、E 为顶点的三角形和以A 、B 、C 为顶点的三角形相似，且相似比为13．（1）根据题意确定D 、E 的位置，画出简图；（2）求AD 、AE 和DE 的长．22、如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的ABC △是格点三角形．在建立平面直角坐标系后，点B 的坐标为（11--，）．（1）把ABC △向左平移8格后得到111A B C △，画出111A B C △的图形并写出点1B 的坐标；（2）把ABC △绕点C 按顺时针方向旋转90后得到22A B C △，画出22A B C △的图形并写出点2B 的坐标；（3）把ABC △以点A 为位似中心放大，使放大前后对应边长的比为1:2，画出33AB C△的图形．23、如图，在平面直角坐标系中，四边形OABC 的顶点坐标分别是O （0，0），A （3，0），B （4，4），C （-2，3），将点O ， A ， B ， C 的横坐标、纵坐标都乘以-2.xyOABC(1)画出以变化后的四个点为顶点的四边形；(2)由（1）得到的四边形与四边形OABC位似吗？如果位似，指出位似中心及与原图形的相似比.答案一、选择题1、B2、B3、C4、C5、D6、C7、C8、A9、C 10、C11、C 12、C 13、C 14、D 15、B二、填空题16、（2，-4）17、（-8，4）或（8，-4）.18、△ABC19、（0，2）（-4，0）20、6三、综合题21、19．（1）两种情况，图略；（2）第一种情况：AD =4，AE =2，DE =83；第二种情况：AD =2，AE =4，DE=83．22、（1）画图略，点1B 的坐标为（9,1--）；（2）画图略，点2B 的坐标为（5,5）；（3）23、（1）解：如图所示，四边形OA′B′C′即为所求四边形；（2）解：∵将点O ， A ， B ， C 的横坐标、纵坐标都乘以-2可得出四边形OA′B′C′， ∴各对应边的比为2，对应点的连线都过原点，∴得到的四边形与四边形OABC 位似，位似中心是O （0，0），与原图形的相似比为2. 【考点】作图-位似变换【解析】（1）将点O ， A ， B ， C 的横坐标、纵坐标都乘以-2得O （0，0），A′（-6，0），B′（-8，-8），C′（4，-6），顺次连接各点即可；（2）根据位似图形的定义可知得到的四边形与四边形OABC 位似，根据图形可得出位似中心及位似比.。

23.5 位似图形1．如果两个图形对应点的连线__交于一点__，并且各对对应点与这个交点所连线段的比值__相等__，那么这两个图形叫做位似图形，这个交点叫做__位似中心__．2．判断位似图形必须具备三个条件：(1)两个图形__相似__；(2)对应点的连线__相交于一点__；(3)对应边互相__平行__或在__同一条直线上__．3．位似图形一定是相似图形；位似图形上任意一对对应点到位似中心的距离之比等于__相似比__．知识点1：位似图形的概念1．下列3个图形中是位似图形的有( B )A．1个B．2个C．3个D．0个2．(2014·东营)下列关于位似图形的表述：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么，这两个图形是位似图形；④位似图形上任意两点与位似中心的距离之比等于位似比．其中正确命题的序号是( A )A．②③ B．①② C．③④ D．②③④3．图中两个四边形是位似图形，它们的位似中心是( D )A．点M B．点N C．点O D．点P知识点2：位似图形的性质4．两个图形中，对应点到位似中心的线段比为2∶3，则这两个图形的相似比为( A ) A．2∶3 B．4∶9C.2∶ 3 D．1∶25．如图，四边形ABCD与四边形AEFG是位似图形，且AC∶AF＝2∶3，则下列结论不正确的是( B )A．四边形ABCD与四边形AEFG是相似图形B．AD与AE的比是2∶3C．四边形ABCD与四边形AEFG的周长比是2∶3D．四边形ABCD与四边形AEFG的面积比是4∶9,第5题图) ,第6题图)6．如图，以点O 为位似中心，将五边形ABCDE 放大后得到五边形A ′B ′C ′D ′E ′，已知OA ＝10 cm ，OA ′＝20 cm ，则五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比值是__12__．知识点3：位似图形的画法7．如图，找出下列图形的位似中心O .解：略8．如图，已知形如木屋架的五边形ABCDE ，点O 在BC 上，以O 点为位似中心把ABCDE缩小到原来的12.解：略9．(2014·玉林)△ABC 与△A′B′C′是位似图形，且△ABC 与△A′B′C′的位似比是1∶2，已知△ABC 的面积是3，则△A′B′C′的面积是( D )A ．3B ．6C ．9D ．1210．如图，五边形ABCDE 和五边形A 1B 1C 1D 1E 1是位似图形，且PA 1＝23PA ，则AB ∶A 1B 1等于( B )A.23B.32C.35D.5311．用作位似图形的方法，可以将一个图形放大或缩小，位似中心位置可选在( D ) A ．原图形的外部 B ．原图形的内部 C ．原图形的边上 D ．任意位置12．如图，下列由位似变换得到的图形中，面积比是1∶9的是( D )13．如图，△ABC 与△A ′B ′C ′是位似图形，点O 是位似图形，若OA ＝2AA ′，S △ABC＝8，则S △A ′B ′C ′＝__18__．14．如图，△ABC 与△A ′B ′C ′是位似图形，且位似比是1∶2，若AB ＝2 cm ，则A ′B ′＝__4__cm ，并在图中画出位似中心O .解：图略 15．如图，已知△DEO 与△ABO 是位似图形，△OEF 与△OBC 是位似图形，试说明：OD ·OC ＝OF ·OA .解：由△DEO 与△ABO 位似得到OD OA ＝OE OB ；由△OEF 与△OBC 位似可得OE OB ＝OF OC .∴OD OA ＝OFOC ，即OD·OC ＝OF·OA16．如图，图中的小方格都是边长为1的正方形，△ABC 与△A ′B ′C ′是关于点O 为位似中心的位似图形，它们的顶点都在小正方形的顶点上．(1)画出位似中心点O；(2)求出△ABC与△A′B′C′的位似比；(3)以点O为位似中心，再画一个△A1B1C1，使它与△ABC的位似比等于1.5.解：(1)略(2)1∶2(3)画图略，寻找A1，B1，C1的方法是OAOA1＝OBOB1＝OCOC1＝23即可17．如图，在6×8的网格图中，每个小正方形的边长均为1，点O和△ABC的顶点均为小正方形的顶点．(1)以O为位似中心，在网格图中作△A′B′C′，使△A′B′C′和△ABC位似，且相似比为1∶2；(2)连接(1)中的AA′，求四边形AA′C′C的周长．(结果保留根号)解：(1)如图（2）四边形AA′C′C的周长＝4＋62。

23.5位似图形1．如果两个图形对应点的连线__交于一点__，并且各对对应点与这个交点所连线段的比值__相等__，那么这两个图形叫做位似图形，这个交点叫做__位似中心__．2．判断位似图形必须具备三个条件：(1)两个图形__相似__；(2)对应点的连线__相交于一点__；(3)对应边互相__平行__或在__同一条直线上__．3．位似图形一定是相似图形；位似图形上任意一对对应点到位似中心的距离之比等于__相似比__．知识点1：位似图形的概念1．下列3个图形中是位似图形的有( B )A．1个B．2个C．3个D．0个2．(2014·东营)下列关于位似图形的表述：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么，这两个图形是位似图形；④位似图形上任意两点与位似中心的距离之比等于位似比．其中正确命题的序号是( A )A．②③B．①②C．③④D．②③④3．图中两个四边形是位似图形，它们的位似中心是( D )A．点M B．点N C．点O D．点P知识点2：位似图形的性质4．两个图形中，对应点到位似中心的线段比为2∶3，则这两个图形的相似比为( A ) A．2∶3 B．4∶9C.2∶ 3 D．1∶25．如图，四边形ABCD与四边形AEFG是位似图形，且AC∶AF＝2∶3，则下列结论不正确的是( B )A．四边形ABCD与四边形AEFG是相似图形B．AD与AE的比是2∶3C ．四边形ABCD 与四边形AEFG 的周长比是2∶3 D ．四边形ABCD 与四边形AEFG 的面积比是4∶9,第5题图) ,第6题图)6．如图，以点O 为位似中心，将五边形ABCDE 放大后得到五边形A ′B ′C ′D ′E ′，已知OA ＝10 cm ，OA ′＝20 cm ，则五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比值是__12__．知识点3：位似图形的画法7．如图，找出下列图形的位似中心O .解：略8．如图，已知形如木屋架的五边形ABCDE ，点O 在BC 上，以O 点为位似中心把ABCDE 缩小到原来的12.解：略9．(2014·玉林)△ABC 与△A′B′C′是位似图形，且△ABC 与△A′B′C′的位似比是1∶2，已知△ABC 的面积是3，则△A′B′C′的面积是( D )A ．3B ．6C ．9D ．1210．如图，五边形ABCDE 和五边形A 1B 1C 1D 1E 1是位似图形，且P A 1＝23P A ，则AB ∶A 1B 1等于( B )A.23B.32C.35D.5311．用作位似图形的方法，可以将一个图形放大或缩小，位似中心位置可选在( D ) A ．原图形的外部 B ．原图形的内部 C ．原图形的边上 D ．任意位置12．如图，下列由位似变换得到的图形中，面积比是1∶9的是( D )13．如图，△ABC 与△A ′B ′C ′是位似图形，点O 是位似图形，若OA ＝2AA ′，S △ABC ＝8，则S △A ′B ′C ′＝__18__．14．如图，△ABC 与△A ′B ′C ′是位似图形，且位似比是1∶2，若AB ＝2 cm ，则A ′B ′＝__4__cm ，并在图中画出位似中心O .解：图略15．如图，已知△DEO 与△ABO 是位似图形，△OEF 与△OBC 是位似图形，试说明：OD ·OC ＝OF ·OA .解：由△DEO与△ABO位似得到ODOA＝OEOB；由△OEF与△OBC位似可得OEOB＝OF OC.∴ODOA＝OFOC，即OD·OC＝OF·OA16．如图，图中的小方格都是边长为1的正方形，△ABC与△A′B′C′是关于点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上．(1)画出位似中心点O；(2)求出△ABC与△A′B′C′的位似比；(3)以点O为位似中心，再画一个△A1B1C1，使它与△ABC的位似比等于1.5.解：(1)略(2)1∶2(3)画图略，寻找A1，B1，C1的方法是OAOA1＝OBOB1＝OCOC1＝23即可17．如图，在6×8的网格图中，每个小正方形的边长均为1，点O和△ABC的顶点均为小正方形的顶点．(1)以O为位似中心，在网格图中作△A′B′C′，使△A′B′C′和△ABC位似，且相似比为1∶2；(2)连接(1)中的AA′，求四边形AA′C′C的周长．(结果保留根号)解：(1)如图（2）四边形AA′C′C 的周长＝4＋62。