九年级数学上册：位似图形练习

图形的相似专题练习1．已知△ABC∽△DEF，AB＝1，BC＝3，EF＝5，则△ABC与△DEF的面积比是()A．1∶9 B．1∶25C．9∶25 D．3∶52．如图，四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形，若OB∶OB′＝2∶3，则四边形ABCD与四边形A′B′C′D′的面积比为()图2A．4∶9 B．2∶5C．2∶3 D．2∶ 33．如果3A＝2B(AB≠0)，那么下列比例式中正确的是()A．ab＝32B．ba＝23C．a2＝b3D．a3＝b24．如图，在△ABC中，点D，E分别为边AB，AC上的点，且DE∥B C．若AD＝5，BD＝10，AE＝3，则CE的长为()图4A．3 B．6C．9 D．125．在下面的图形中，相似的一组是(),A) ,B),C) ,D)图56．如图所示，小正方形的边长均为1，则下列选项中阴影部分的三角形与△ABC相似的是(),A) ,B),C) ,D)图67．为测量某河的宽度，小在河对岸选定一个目标点A，再在他所在的这一侧选点B，C，D，使得AB⊥BC，CD⊥BC，然后找出AD与BC的交点E，如图所示．若测得BE＝90 m，EC＝45 m，CD＝60 m，则这条河的宽AB等于()图7A．120 m B．67.5 mC．40 m D．30 m8．如图，在△ABC中，∠A＝70°，AB＝4，AC＝6，将△ABC沿图中的虚线剪开，则剪下的阴影三角形与原三角形不相似的是(),A) ,B),C) ,D)图89．如图，在△ABC 中，D ，E 两点分别在AB ，AC 边上，DE ∥B C ．如果ADDB ＝32，AC ＝10，那么EC ＝________．图910．如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P 处放一水平的平面镜，光线从点A 出发经平面镜反射后刚好到古城墙CD 的顶端C 处．已知AB ⊥BD ，CD ⊥BD ，测得AB ＝2米，BP ＝3米，PD ＝15米，那么该古城墙的高度CD 是_________米．图1011．如图，比例规是一种画图工具，它由长度相等的两脚AD 和BC 交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方(即同时使OA ＝3OD ，OB ＝3OC )，然后张开两脚，使A ，B 两个尖端分别在线段l 的两个端点上，若CD ＝3.2 cm ，则AB 的长为_________ cm.图1112．如图，已知矩形纸片ABCD 中，AB ＝1，剪去正方形ABEF ，得到的矩形ECDF 与矩形ABCD 相似，则AD 的长为__________．图1213．如图，在平面直角坐标系xOy中，以原点为位似中心，线段AB与线段A′B′是位似图形，若A(－1，2)，B(－1，0)，A′(－2，4)，则B′的坐标为___________．图1314．如图，在平面直角坐标系中，△OAB的顶点坐标分别为O(0，0)，A(2，1)，B(1，－2)．(1)以原点O为位似中心，在y轴的右侧画出△OAB的一个位似△OA1B1，使它与△OAB的位似比为2∶1，并分别写出点A，B的对应点A1，B1的坐标；(2)画出将△OAB向左平移2个单位，再向上平移1个单位后得△O2A2B2，并写出点A，B的对应点A2，B2的坐标；(3)△OA1B1和△O2A2B2是位似图形吗？若是，请在图中标出位似中心M，并写出点M的坐标．图1415．如图，在四边形ABCD中，AD∥BC，AB⊥BC，点E在AB上，∠DEC ＝90°.(1)求证：△ADE∽△BEC；(2)若AD＝1，BC＝3，AE＝2，求AB的长．图1516．如图，在正方形ABCD中，点E在边BC上(点E不与点B重合)，连接AE，过点B作BF⊥AE于点F，交CD于点G.(1)求证：△ABF∽△BGC；(2)若AB＝2，G是CD的中点，求AF的长．图1617．如图，BD，CE分别是△ABC的两边上的高，过D作DG⊥BC于G，分别交CE及BA的延长线于F，H，求证：(1)DG2＝BG·CG；(2)BG·CG＝GF·GH.图1718．如图，一圆柱形油桶，高1.5 m，用一根2 m长的木棒从桶盖小口斜插桶内，至另一端的B处，抽出木棒后，量得上面没浸油的部分为1.2 m，求桶内油面高度．图1819．如图，操场上有一根旗杆AH，为测量它的高度，在B和D处各立一根高1.5米的标杆BC，DE，两杆相距30米．测得视线AC与地面的交点为F，视线AE与地面的交点为G，并且H，B，F，D，G都在同一直线上，测得BF为3米，DG为5米，求旗杆AH的高度．图1920．如图1，把两块全等的含45°角的直角三角板ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合．把三角板ABC 固定不动，让三角板DEF绕点D旋转，两边分别与线段AB，BC相交于点P，Q，易说明△APD∽△CDQ.根据以上内容，回答下列问题：(1)如图2，将含30°角的三角板DEF(其中∠EDF＝30°)的锐角顶点D与等腰△ABC(其中∠ABC＝120°)的底边中点O重合，两边DF，DE分别与边AB，BC 相交于点P，Q.写出图中的相似三角形__△APD∽△CDQ__(直接填在横线上)；(2)其他条件不变，将三角板DEF旋转至两边DF，DE分别与边AB的延长线、边BC相交于点P，Q.上述结论还成立吗？请你在图3上补全图形，并说明理由；(3)在(2)的条件下，连接PQ，△APD与△DPQ是否相似？请说明理由；(4)根据(1)(2)的解答过程，你能否将两三角板改为更一般的三角形，使得(1)中的结论仍然成立？若能，请说明两个三角形应满足的条件；若不能，请简要说明理由．,图1),图2),图3)图20参考答案【过关训练】1．C2．A3．C4．B5．C6．A7．A8．D 9．__4__10．__10__11．_9.6__12．_1＋52__13．(－2，0)_14．解：(1)如答图，△OA1B1为所作，点A1，B1的坐标分别为(4，2)，(2，－4)；(2)如答图，△O2A2B2为所作，点A2，B2的坐标分别为(0，2)，(－1，－1)；(3)△OA1B1和△O2A2B2是位似图形，如答图，点M为所，位似中心M的坐标为(－4，2)．15．[解：(1)证明：∵AD∥BC，AB⊥BC，∴AB⊥AD，∠A＝∠B＝90°，∴∠ADE＋∠AED＝90°.∵∠DEC＝90°，∴∠AED＋∠BEC＝90°，∴∠ADE＝∠BEC，∴△ADE∽△BE C．(2)∵△ADE∽△BEC，∴BEAD＝BCAE，即BE1＝32，∴BE＝3 2，∴AB＝AE＋BE＝7 2.16．解：(1)证明：∵四边形ABCD是正方形，∴∠ABE＝∠BCG＝90°.∵BF⊥AE，∴∠BAE＋∠ABF＝90°，∠CBG＋∠ABF＝90°，∴∠BAE＝∠CBG，∴△ABF∽△GB C．(2)∵△ABF∽△BG C．∴ABBG＝AFBC.∵AB＝2，G是CD的中点，四边形ABCD是正方形，∴BC＝2，CG＝1，∴BG＝BC2＋CG2＝5，∴25＝AF2，解得AF＝45 5.17．证明：(1)∵BD⊥AC，DG⊥BC，∴∠BDC＝∠DGC＝90°，∴∠DBC＋∠DCG＝∠GDC＋∠DCG，∴∠GDC＝∠DBC，∴△BDG∽△DCG，∴BG∶DG＝DG∶CG，即DG2＝BG·CG.(2)同(1)中的方法，同理可证△BGH∽△FGC，∴BG∶GF＝GH∶CG，∴BG·CG＝GF·GH.18．解：∵DE∥BC，∴△ADE∽△ABC，∴AEAC＝ADAB，即AE1.5＝1.22，解得AE＝0.9 m，∴EC＝1.5－0.9＝0.6(m)，即油面高0.6 m. 19．解：设AH＝x，BH＝y，由题意知，△AHF∽△CBF，△AHG∽△EDG，∴BFHF＝CBAH，DGHG＝DEAH，∴3x＝1.5×(y＋3)，5x＝1.5×(y＋30＋5)，解得x＝24.则旗杆AH的高度为24 m.20．__△APD∽△CDQ__解：(2)成立，如答图．理由如下：∵AB＝BC，∴∠BAC＝∠BC A．∵∠ABC＝120°，∴∠BAC＝∠BCA＝30°，∴∠ADP＋∠APD＝180°－30°＝150°.∵∠EDF＝30°，∴∠ADP＋∠CDQ＝150°，∴∠APD＝∠CDQ，∴△APD∽△CDQ. (3)△APD∽△DPQ.理由如下：∵△APD∽△CDQ，∴APCD＝DPDQ.∵点D为AC的中点，∴CD＝AD，∴APAD＝DPDQ，即APDP＝ADDQ.又∵∠P AD＝∠PDQ＝30°，∴△APD∽△DPQ.(4)△DEF满足∠EDF＝α，△ABC满足顶角为(180°－2α)的等腰三角形即可．理由：∵∠ABC＝180°－2α，∴∠A＝∠C＝α.∵∠ADP＋∠APD＝180°－α，∠ADP＋∠QDC＝180°－α，∴∠APD＝∠CDQ.又∵∠A＝∠C，∴△APD∽△CDQ.。

如何画位似图形位似变换是新课程标准中涉及的一个重要知识点，它是图形变换的一种，实际上它是相似变换的一种特殊情形，存在位似中心———即对应顶点连线的交点．其位似比就是相似比．作为一个新的知识点，越来越受到中考命题者的青睐．图形放大、缩小通常用位似变换的思想作图，位似中心的位置可在图形顶点处、图形边上、图形内部、图形外部．本文以一道中考题为例介绍几种常见画法，供同学们参考．（锦州）如图1，己知四边形ABCD ，用尺规将它放大，使放大前后的图形对应线段的比为1:2．画法一：延长AD 到1D ，使1DD AD =，延长AC 到点1C ，使1CC AC =，延长AB 到点1B ，使1BB AB =，连接11D C ，11C B ，则四边形1111A B C D 即为所求（如图2）． 说明：延长AD 得到1D 后，也可以过点1D 作11D C DC ∥，交AC 的延长线于1C ，再过点1C 作11B C BC ∥，交AC 的延长线于1B ，得到四边形1111A B C D ．画法二：延长DA 到点1D ，使12AD AD =，延长CA 到点1C ，使12AC AC =，延长BA 到点1B ，使12AB AB =连接11B C ，11C D ，则四边形1111A B C D 即为所求（如图3）．画法三：任取一点O ，连接OA 并延长到点1A ，使1AA OA =，连接OB 并延长到点1B ，使1BB OB =、连接OC 并延长到点1C ，使1CC OC =，连接OD 并延长到点1D ，使1DD OD =，顺次连接11A B ，11B C ，11C D ，11D A ，则四边形1111A B C D 即为所求（如图4）． 运用这些作图方法可以解决不少数学问题．现举例说明：例 如图5，在给定的锐角ABC △中，求作一个正方形DEFG ，使D E ，落在BC 上，F G ，分别落在AC AB ，边上，要求写出画法． 画法：第一步：画一个有三个顶点落在ABC △两边上的正方形D E F G ''''（如图5）；第二步：连接BF '并延长交AC 于点F ；第三步：过F 点作FE BC ⊥，垂足为点E ；第四步：过F 作FG BC ∥交AB 于点G ；第五步：过G 作GD BC ⊥，垂足为点D ．四边形DEFG 即为所求的正方形．（如图5）想一想：为什么四边形DEFG 是正方形？请读者思考．。

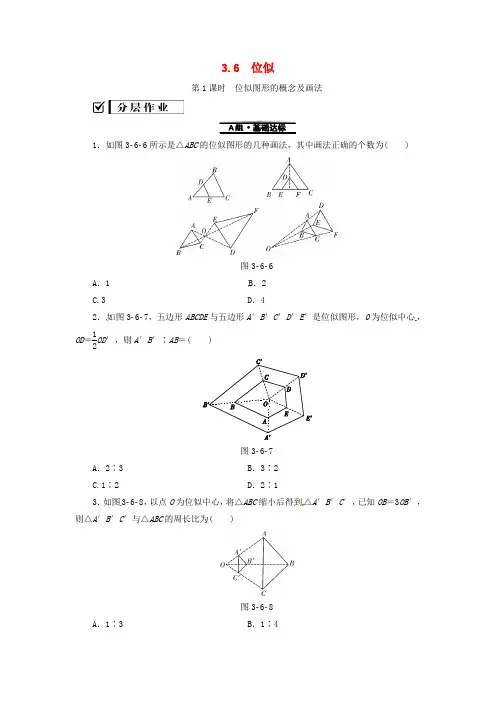
3.6 位似第1课时 位似图形的概念及画法1．如图3­6­6所示是△ABC 的位似图形的几种画法，其中画法正确的个数为( )图3­6­6A ．1B ．2 C.3D ．42．如图3­6­7，五边形ABCDE 与五边形A ′B ′C ′D ′E ′是位似图形，O 为位似中心，OD ＝12OD ′，则A ′B ′∶AB ＝( )图3­6­7A ．2∶3B ．3∶2 C.1∶2D ．2∶13．如图3­6­8，以点O 为位似中心，将△ABC 缩小后得到△A ′B ′C ′，已知OB ＝3OB ′，则△A ′B ′C ′与△ABC 的周长比为( )图3­6­8A ．1∶3B ．1∶4C.1∶5 D ．1∶94．[2018·青海]如图3­6­9，四边形ABCD 与四边形EFGH 位似，其位似中心为点O ，且OE EA ＝43，则FGBC＝________.图3­6­95．如图3­6­10，△ABC 与△A ′B ′C ′是位似图形，且位似比是1∶2.若AB ＝2 cm ，则A ′B ′＝________ cm ，请在图中画出位似中心O .图3­6­106．[2018春·邕宁区校级期中]如图3­6­11，以点O 为位似中心，将四边形ABCD 放大为原来的2倍(只需画出一种情况即可)．图3­6­117．图3­6­12中小方格是边长为1的正方形，△ABC 与△A ′B ′C ′是以点O 为位似中心的位似图形，它们的顶点都在小正方形的顶点上．(1)画出位似中心O ；(2)求△ABC 与△A ′B ′C ′的相似比．图3­6­128．[2018·安徽]如图3­6­13，在由边长为1个单位长度的小正方形组成的10×10网格中，已知点O ，A ，B 均为网格线的交点．(1)在给定的网格中，以点O 为位似中心，将线段AB 放大为原来的2倍，点A ，B 的对应点分别为A 1，B 1，画出线段A 1B 1；(2)将线段A 1B 1绕点B 1逆时针旋转90°得到线段A 2B 1，画出线段A 2B 1； (3)以A ，A 1，B 1，A 2为顶点的四边形AA 1B 1A 2的面积是________个平方单位．图3­6­13 参考答案1．D 2.D 3.A 4.47 5.46．略 7.(1)略 (2)1∶2 8．(1)略 (2)略 (3)20。

一、选择题1．如图，在平行四边形ABCD 中，E 是DC 上的点，:3:2DE EC =，连接AE 交BD 于点F ，则DEF 与DAF △的面积之比为（ ）A ．2:5B ．3:5C ．4:25D ．9:25 2．如图，////AB CD EF ，若3BF DF =，则AC CE 的值是（ ）A ．2B ．12C ．13D ．33．点B 把线段AC 分成两部分，如果BC AB AB AC =＝k ，那么k 的值为（ ） A ．512+ B ．51- C ．5＋1 D ．5－1 4．古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点G 将一线段MN 分为两线段MG 、GN ，使得其中较长的一段MG 是全长MN 与较短的一段GN 的比例中项，即满足512MG GN MN MG -==，后人把512-这个数称为“黄金分割数”，把点G 称为线段MN 的“黄金分割点”．如图，在△ABC 中，已知AB ＝AC ＝3，BC ＝4，若点D 是边BC 边上的一个“黄金分割点”，则△ADC 的面积为（ ）A ．55B ．355C ．205-D ．1045-5．若2x ＝5y ，则x y的值是（ ） A ．25 B ．52 C ．45 D ．546．如图，已知∠1＝∠2，那么添加一个条件后，仍不能判定△ABC 与△ADE 相似的是（ ）A ．∠C ＝∠AEDB ．∠B ＝∠DC ．AB BC AD DE = D ．AB AC AD AE = 7．若275x y z ==，则2x y z x z +-+的值是（ ） A ．67 B ．13C ．49D ．4 8．若34,x y =则x y=（ ） A ．34 B ．74 C ．43D ．73 9．已知点P 是线段AB 的黄金分割点（AP PB >），2AB =，那么AP 的长约为（ ）A ．0.618B ．1.382C ．1.236D ．0.764 10．如图，矩形ABCD 中，6AB =，8BC =，动点P 从A 点出发，按A B C →→的方向在AB 和BC 上移动，记PA x =，点D 到直线PA 的距离为y ，则y 关于x 的函数图象大致是（ ）A ．B ．C ．D ．11．如图，E 是平行四边形ABCD 的BA 边的延长线上的一点，CE 交AD 于点F ．下列各式：①AE AB ＝AF BC ；②AE AB ＝AF DF ；③AE AB ＝FE FC；④AE BE ＝AF BC ．其中成立的是（ ）A ．③B ．③④C ．②③④D ．①②③④ 12．如图，在四边形ABCD 中，如果ADC BAC ∠=∠，那么下列条件中不能判定ADC 和BAC 相似的是（ ）A ．DAC ABC ∠=∠B ．CA 是BCD ∠的平分线C ．AD DC AB AC= D ．2AC BC CD =⋅ 二、填空题13．如图所示是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地面上形成阴影（圆形）的示意图．已知桌面的半径为0.8m ，桌面距离地面1m ，若灯泡距离地面3m ，则地面上阴影部分的面积为_________m 2（结果保留)π．14．如图，已知在Rt ABC 中，C 90∠=︒，AC 3=，BC 4=，分别将Rt ABC 的三边向外平移2个单位并适当延长，得到111A B C △，则111A B C △的面积为______．15．如图，直线122y x =-+与坐标轴分别交于点,A B ，与直线12y x =交于点,C Q 是线段OA 上的动点，连接CQ ，若OQ CQ =，则点Q 的坐标为___________．16．如图，在平面直角坐标系中，点(0,6)A ，(8,0)B ，点C 是线段AB 的中点，过点C 的直线l 将AOB 截成两部分，直线l 交折线A O B --于点P ．当截成两部分中有三角形与AOB 相似时，则点P 的坐标为__________．17．在Rt △ABC 中，AB =6，AC =5，点D 在边AB 上，且AD =2，点E 在边AC 上，当△ADE ∽△ABC 时，AE =____．18．已知点P 在线段AB 上，且AP ∶PB =2∶3，则PB ∶AB =____．19．如图，若ABC 与DEF 都是正方形网格中的格点三角形（顶点在格点上），则DEF 与ABC 的周长比为_________．20．如图所示，在矩形ABCD 中，3AB =6BC =E 在对角线BD 上，且1.8BE =，连结AE 并延长交DC 于点F ，则CF CD=________．三、解答题21．如图，正方形ABCD 中，6AB =，点E 在边CD 上，且3CD DE =．将ADE 沿AE 翻折至AFE △，延长EF 交边BC 于点G ，连接AG 、CF ．（1）求证：BG GC =；（2）求CFG △的面积．22．如图，在平行四边形ABCD 中，点E 是AC 上一点，射线BE 与CD 的延长线交于点P ，与边AD 交于点F ，连接FC ．（1）若∠ABF ＝∠ACF ，求证：CE 2＝EF •EP ；（2）若点D 是CP 中点，BE ＝23，求EF 的长．23．体验：如图1，在四边形ABCD 中，AB ∥CD ，∠B ＝90°，点M 在BC 边上，当∠AMD ＝90°时，可知△ABM △MCD （不要求证明）．探究：如图2，在四边形ABCD 中，点M 在BC 上，当∠B ＝∠C ＝∠AMD 时，求证：△ABM ∽△MCD ．拓展：如图3，在△ABC 中，点M 是边BC 的中点，点D 、E 分别在边AB 、AC 上．若∠B ＝∠C ＝∠DME ＝45°，BC ＝2CE ＝6，求DE 的长．24．如图，Rt ABC 中，90,ACB AC BC ∠=︒=，P 为ABC 内部一点，且135APB BPC ∠=∠=︒．（1）求证：PAB PBC △∽△；（2）若2PA =，求PB ；（3）若点P 到三角形的边AB ，BC ，CA 的距离分别为123,,h h h ，请直接写出123,,h h h 之间满足关系．25．如图，在平面直角坐标系中，ABC 的三个顶点坐标分别为(1,3),(2,3),(2,1)A B C ----．（1）画出ABC 关于原点O 成中心对称的111A B C △，并写出点1C 的坐标； （2）以原点O 为位似中心，在x 轴上方画出ABC 放大2倍后的222A B C △，并直接写出点2C 的坐标．26．如图，在平面直角坐标系中，ABC 的顶点为()()()2,1,1,3,4,1A B C ，若111A B C △与ABC 是以坐标原点О为位似中心的位似图形，且1A 的坐标为()4,2，请画出111A B C △，并给出顶点11,B C 的坐标．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】由平行四边形的性质得出CD ∥AB ，进而得出△DEF ∽△BAF ，再利用相似三角形的性质可得35EF DE AF BA ==，然后利用高相同的三角形面积比等于底的比得出结果． 【详解】解：∵四边形ABCD 为平行四边形，∴CD ∥AB ，∴∠EDF=∠ABF ，∠DEF=∠BAF ，∴△DEF ∽△BAF ．∵DE ：EC=3：2， ∴33325DE BA ==+， ∴35EF DE AF BA ==， 设点D 到AE 的距离为h ， ∴D 132152DEF AF EF h S S AF AF E h F ⋅===⋅． 故选择：B ．【点睛】本题考查了相似三角形的性质与判定及平行四边形的性质，解题的关键是掌握同高三角形的面积比等于底的比．2．A解析：A【分析】由BF=3DF ，得BD=2DF ，使用平行线分线段成比例定理计算即可.【详解】∵BF=3DF ，∴BD=2DF ，∵////AB CD EF ， ∴AC CE =BD DF ， ∴AC CE =2DF DF=2， 故选A.【点睛】本题考查了平行线分线段成比例定理，熟练掌握定理，特别是定理的对应关系是解题的关键.3．B解析：B【分析】设AC=1，由题意得AB=k ，BC=2k ，由AC=AB+ BC=1得到关于k 的一元二次方程，解方程即可．【详解】设AC=1， ∵BC AB AB AC==k ，且0k >， ∴AB=k ，BC=2k ，∵AC=AB+ BC=1，∴21k k +=，即210k k +-=，∵1a =，1b =，1c =-，()224141150b ac =-=-⨯⨯-=>，∴12k -±=(负值舍去)，∴k = 故选：B ．【点睛】本题考查了比例线段，公式法解一元二次方程，由比例线段得到一元二次方程是解题的关键．4．A解析：A【分析】作AF ⊥BC ，根据等腰三角形ABC 的性质求出AF 的长，再根据黄金分割点的定义求出CD 的长度，利用三角形面积公式即可解题．【详解】解：过点A 作AF ⊥BC ，∵AB=AC ，∴BF=12BC=2， 在Rt ABF ，AF=2222325AB BF -=-=，∵D 是边BC 的两个“黄金分割”点， ∴51CD BC -=即514CD -=， 解得CD=252-，∴12ADC C AF S D ⨯⨯==()125252⨯-⨯=55-， 故选：A ．【点睛】本题考查了“黄金分割比”的定义、等腰三角形的性质、勾股定理的应用以及三角形的面积公式，求出DC 和AF 的长是解题的关键．5．B解析：B【分析】利用内项之积等于外项之积进行判断．【详解】解：∵2x ＝5y ，∴52x y =． 故选：B ．【点睛】本题考查了比例的性质：熟练掌握比例的性质（内项之积等于外项之积，合比性质，分比性质，合分比性质，等比性质）．6．C解析：C【分析】根据已知及相似三角形的判定方法对各个选项进行分析，从而得到最后答案．【详解】解：∵∠1＝∠2∴∠DAE ＝∠BAC∴A ，B ，D 都可判定△ABC ∽△ADE选项C 中不是夹这两个角的边，所以不相似，故选：C ．【点睛】本题考查了相似三角形的判定：①如果两个三角形的三组对应边的比相等，那么这两个三角形相似；②如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；③如果两个三角形的两个对应角相等，那么这两个三角形相似．7．C解析：C【分析】 根据275x y z k ===，则x ＝2k ，y ＝7k ，z ＝5k ，代入2x y z x z+-+进行计算即可． 【详解】 解：275x y z k ===（k≠0）， 则x ＝2k ，y ＝7k ，z ＝5k ， ∴2x y z x z+-+＝2754495k k k k k +-+=， 故选：C ．【点睛】 本题考查了比例的性质，解题的关键是掌握比例的性质进行解题．8．C解析：C【分析】根据比例的性质，两内项之积等于两外项之积进行计算即可求解．【详解】由比例的性质，由34,x y =得43x y =． 故选C ．【点睛】本题考查了比例的性质，利用比例的性质是解题关键．9．C解析：C【分析】根据黄金分割点的定义，由题意知AP 是较长线段；则AP=15-+AB ，代入数据即可． 【详解】解：∵线段AB=2，点P 是线段AB 的黄金分割点（AP PB >）， ∴AP=15-+AB=15-+≈1.236 故选：C 【点睛】本题考查了黄金分割点的概念，熟记黄金分割的比值是解题的关键．10．A解析：A【分析】①点P 在AB 上时，点D 到AP 的距离为AD 的长度，②点P 在BC 上时，根据同角的余角相等求出∠APB=∠PAD ，再利用相似三角形的列出比例式整理得到y 与x 的关系式，从而得解．【详解】解：①当点P 在AB 上运动时，D 到PA 的距离8y AD ==，∴当06x ≤≤时，8y =，②当P 在BC 上运动时，∵∠APB+∠BAP=90°，∠PAD+∠BAP=90°，∴∠APB=∠PAD ，又∵∠B=∠DEA=90°，∴△ABP ∽△DEA ，∴AB AP DE AD=，即：68x y =， ∴当610x <≤时，48y x =，∴()()80648610x y x x ⎧≤≤⎪=⎨<≤⎪⎩， 即当06x ≤≤时，函数图象为平行于x 轴的线段，且8y =；当610x <≤时，函数图象为反比例函数，故选项A 符合题意，故选：A ．【点睛】本题考查动点问题函数图象，解题关键是利用相似三角形的判定与性质，难点在于根据点Ｐ的位置分情况讨论．11．C解析：C【分析】根据平行四边形的性质得到AB ∥CD ，AB=CD ，由△AEF ∽△DCF 得到AE AF EF CD DF FC ==，用AB 等量代换CD ，得到AE AF EF AB DF FC==；再利用AF ∥BC ，由△AEF ∽△BEC 得AE AF BE BC=，由此可判断． 【详解】解：∵四边形ABCD 为平行四边形，∴AB ∥CD ，AB=CD ；∴△AEF ∽△DCF ， ∴AE AF EF CD DF FC ==，而AB=CD ， ∴AE AF EF AB DF FC== ∴②③正确；又∵AF ∥BC ，∴△AEF ∽△BEC ， ∴AE AF BE BC=， ∴④正确，①不正确；故选：C ．【点睛】本题考查了平行四边形的性质，相似三角形的判定与性质．熟知相似三角形的判定定理是解答此题的关键．12．D解析：D【分析】已知∠ADC ＝∠BAC ，则A 、B 选项可根据有两组角对应相等的两个三角形相似来判定；C 选项可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定；D 选项虽然也是对应边成比例但无法得到其夹角相等，所以不能推出两三角形相似.【详解】在△ADC 和△BAC 中，∠ADC ＝∠BAC ，如果△ADC ∽△BAC ，需满足的条件有：①∠DAC ＝∠ABC 或AC 是∠BCD 的平分线； ②AD DC AB AC=； 故选：D ．【点睛】 此题主要考查了相似三角形的判定方法；熟记三角形相似的判定方法是解决问题的关键．二、填空题13．44π【分析】证明△OBQ ∽△OAP 根据相似三角形的性质求出AP 根据圆的面积公式计算得到答案【详解】解：如图由题意得OB=08mOQ=OP-PQ=3-1=2（m ）BQ ∥AP ∴△OBQ ∽△OAP ∴即解解析：44π【分析】证明△OBQ ∽△OAP ，根据相似三角形的性质求出AP ，根据圆的面积公式计算，得到答案．【详解】解：如图，由题意得，OB=0.8m ，OQ=OP-PQ=3-1=2（m ），BQ ∥AP ，∴△OBQ ∽△OAP ，∴BQ OQ AP OP =，即0.823AP =， 解得，AP=1.2（m ）， 则地面上阴影部分的面积=π×1.22=1.44π（m 2），故答案为：1.44π．【点睛】本题考查的是相似三角形的应用，掌握相似三角形的判定定理和性质定理是解题的关键．14．54【分析】作于点D 作于点E 作于点F 分别证明△和△求出和再根据三角形面积公式求解即可【详解】解：作于点D 作于点E 作于点F ∵三边向外平移个单位∴∵∴∠且∠∴△∴又∵∠且∠∴△∴∴∴又∵△∴∴∴【点睛】 解析：54【分析】作11CD B C ⊥于点D ，作11BE B C ⊥于点E ，作11BF A B ⊥于点F ，分别证明△ACB BFG ∆∽和△1GHB ACB ∆∽，求出11A C 和11B C ，再根据三角形面积公式求解即可．【详解】解：作11CD B C ⊥于点D ，作11BE B C ⊥于点E ，作11BF A B ⊥于点F ，∵Rt ABC ∆三边向外平移个单位，∴1=22,2,C D CD BE GH BF ====，∵11//AB A B∴∠ABC AGC =∠且∠90ACB BFG =∠=︒∴△ACB BFG ∆∽ ∴103BG = 又∵∠11B A GC ABC =∠=∠，且∠190GHB ACB =∠=︒∴△1GHB ACB ∆∽ ∴1AC GH BC B H= ∴183B H = ∴1111C B CD DE EH HB =+++1082433=+++12=又∵△111ABC A B C ∆∽ ∴1111AC B C AC BC= ∴119A C = ∴111111112A B C S AC B C ∆=⨯⨯ 11292=⨯⨯ 54=【点睛】此题主要考查了相似三角形的性质与判定，能正确作出辅助线证明三角形是解答此题的关键．15．【分析】与联立组成方程组求出点C 的坐标为（21）从而可判断点C 是AB 的中点所以OC=AC 从而得到∠AOC=∠OAC 又因为所以∠AOC=∠OCQ 从而可判断△OCQ ∽△OAC 再根据相似三角形的性质可得最 解析：5,04⎛⎫ ⎪⎝⎭【分析】122y x =-+与12y x =联立组成方程组求出点C 的坐标为（2，1）从而可判断点C 是AB 的中点，所以OC=AC ，从而得到∠AOC=∠OAC ，又因为OQ CQ =，所以∠AOC=∠OCQ ，从而可判断△OCQ ∽△OAC ，再根据相似三角形的性质可得OQ OC OC OA =，最后把数值代入求出OQ 的长，从而得到Q 点的坐标．【详解】解：如图所示，依题意得：12212y x y x ⎧=-+⎪⎪⎨⎪=⎪⎩解得：21x y =⎧⎨=⎩ ∴点C 的坐标为（2，1） 对于直线122y x =-+，令x=0，解得y=2， 令y=0，解得x=4．∴点A ，B 的坐标分别为（4，0），（0，2）．∴点C 是AB 的中点．∵△OAB 为直角三角形，∴OC=AC ，∴∠AOC=∠OAC ，∵OQ CQ =，∴∠AOC=∠OCQ ，∴∠AOC=∠OCQ=∠OAC ，∴△OCQ ∽△OAC ， ∴OQ OC OC OA = 又∵△OAB 为直角三角形，OA=4，OB=2，∴222224AB OB OA =+=+=25 ∴OC=AC=12AB =5 ∴55=， 解得：OQ=54， ∴点Q 的坐标为（54，0）．故答案为：（54，0）． 【点睛】 本题考查了一次函数与二元一次方程，等腰三角形的性质及相似三角形的判定和性质，掌握相关知识是解题的关键．16．或或【分析】分三种情况讨论当时则则当时由则当时则则再利用相似三角形的性质求解的坐标即可【详解】解：点是线段的中点当时则如图当时由如图当时则综上：或或故答案为：或或【点睛】本题考查的是坐标与图形三角形 解析：(0,3)或(4,0)或70,4⎛⎫ ⎪⎝⎭ 【分析】分三种情况讨论，当PC OA ⊥时，则//,PC OB 则APC AOB ∽，当PC AB ⊥时，由90,,PCB AOB PBC ABO ∠=∠=︒∠=∠ 则BCP BOA △∽△，当CP OB ⊥时，则//,PC OA 则,BCP BAO ∽ 再利用相似三角形的性质求解P 的坐标即可．【详解】解：()()06,8,0,A B ， 点C 是线段AB 的中点， 226,8,6810,OA OB AB ∴===+= 15,2AC AB == 当PC OA ⊥时，则//,PC OB ∴ APC AOB ∽，,AP AC AO AB ∴= 162AP ∴=， ()3,0,3,AP P ∴=如图，当PC AB ⊥时，由90,,PCB AOB PBC ABO ∠=∠=︒∠=∠∴ BCP BOA △∽△，,BC BP BO BA∴= 5,810BP ∴= 25,4BP ∴= 2578,44OP ∴=-=7,0,4P ⎛⎫∴ ⎪⎝⎭如图，当CP OB ⊥时，则//,PC OA,BCP BAO ∴∽,BC BP BA BO∴= 1,28BP ∴= 4,BP ∴=4,OP ∴=()4,0.P ∴综上：()0,3P 或7,04P ⎛⎫ ⎪⎝⎭或()4,0.P 故答案为：()0,3P 或7,04P ⎛⎫⎪⎝⎭或()4,0.P 【点睛】本题考查的是坐标与图形，三角形相似的判定与性质，掌握以上知识是解题的关键． 17．【分析】根据相似三角形的对应边成比例求解即可求得答案【详解】解：∵△ADE ∽△ABC ∴即解得：AE ＝；故答案为：【点睛】此题考查了相似三角形的性质掌握相似三角形的性质是解题的关键 解析：53【分析】根据相似三角形的对应边成比例求解，即可求得答案．【详解】解： ∵△ADE ∽△ABC ， ∴AD AE AB AC=，即265AE =， 解得：AE ＝53； 故答案为：53． 【点睛】此题考查了相似三角形的性质．掌握相似三角形的性质是解题的关键．18．3∶5（或）【分析】根据比例的性质直接求解即可【详解】解：由题意AP:PB=2:3∴PB:AB=PB:(AP+PB)=3:(2+3)=3:5；故答案是：3:5（或）【点睛】本题主要考查比例问题关键是解析：3∶5（或35） 【分析】根据比例的性质直接求解即可．【详解】解：由题意AP:PB=2:3，∴PB :AB = PB :(AP+PB)=3:(2+3)=3:5；故答案是：3:5（或35）． 【点睛】本题主要考查比例问题，关键是根据比例的性质解答． 19．【分析】设正方形网格的边长为1根据勾股定理求出△EFD △ABC 的边长运用三边对应成比例则两个三角形相似这一判定定理证明△EDF ∽△BAC 即可解决问题【详解】解：设正方形网格的边长为1由勾股定理得：D【分析】设正方形网格的边长为1，根据勾股定理求出△EFD 、△ABC 的边长，运用三边对应成比例，则两个三角形相似这一判定定理证明△EDF ∽△BAC ，即可解决问题．【详解】解：设正方形网格的边长为1，由勾股定理得：DE 2＝22+22，EF 2＝22+42，∴DE＝EF ＝同理可求：AC ，BC∵DF ＝2，AB ＝2，∴1EF DE DF BC AB AC ===∴△EDF ∽△BAC ，∴DEF 与ABC，．【点睛】本题主要考查了勾股定理和相似三角形的判定及其性质，熟练掌握相似三角形的判定与性质是解题的关键．20．【分析】根据勾股定理求出BD 的长度得到DE 的长根据相似三角形的性质得到对应线段成比例计算可求出DF 的长求出CF 计算得出CF 与CD 的比值即可【详解】解：∵四边形ABCD 是矩形∴∵∴∵∴∵∴∴解得：则∴ 解析：13【分析】根据勾股定理求出BD 的长度，得到DE 的长，根据相似三角形的性质得到对应线段成比例，计算可求出DF 的长，求出CF ，计算得出CF 与CD 的比值即可．【详解】解：∵四边形ABCD 是矩形，∴90BAD ∠=︒， ∵AB ==BC ∴3BD ==．∵ 1.8BE =，∴3 1.8 1.2DE =-=．∵//AB CD ，∴ABE FDE ∽△△ ∴ 1.21.8DF DE AB BE ==，解得：DF =，则CF CD DF =-=∴13CF CD ==． 故答案为：13． 【点睛】本题主要考查了矩形的性质、相似三角形的判定和性质，掌握矩形的性质定理和相似三角形的判定定理、性质定理是解题的关键．三、解答题21．（1）见解析；（2）18 5【分析】（1）由条件可以求出ED的值，设FG=x，则BG=FG=x，CG=6-x，EG=x+2，由勾股定理可以求出x的值，从而可以求出BG和CG的值，得出结论．（2）过点F作FN⊥CG于点N，可以得出∠FNG=∠DCG=90°，通过证明△GFN∽△GEC，得出GF FNGE EC=，可以求出FN的值，最后利用三角形的面积公式可以求出其面积．【详解】解：（1）证明：∵AB=6，CD=3DE，∴DC=6，∴DE=2，CE=4，∴EF=DE=2，设FG=x，则BG=FG=x，CG=6-x，EG=x+2，在Rt△ECG中，由勾股定理得，42+（6-x）2=（x+2）2，解得x=3，∴BG=FG=3，CG=6-x=3，∴BG=CG．（2）过点F作FN⊥CG于点N，则∠FNG=∠DCG=90°，又∵∠EGC=∠EGC，∴△GFN∽△GEC，∴GF FN GE EC=，∴354FN =，∴FN=125，∴S△CGF=12CG•FN＝112325⨯⨯=185．【点睛】本题考查了正方形的性质，相似三角形的判定与性质，勾股定理的运用及三角形面积公式的运用．在解答中注意相似三角形的对应顶点在对应的位置．22．（1）见解析；（2）EF=【分析】（1）由平行四边形的性质可得∠ABF BPC =∠，又∠ABF ＝∠ACF ，可得ACF BPC ∠=∠，又FEC PEC ∠=∠可证△FEC CEP ∆∽，从而可得结论；（2）证明△PFD PBC ∆∽得1122DF BC AD ==，由∠,AEB PEC ABE BPC =∠∠=∠可证明△ABE CPE ∆∽可求得PE =EF EP PF =-可得结论．【详解】解：（1）由题可知，∠ABF ＝∠ACF ，又∵四边形ABCD 为平行四边形，∴AB//CD∴∠ABF BPC =∠∴∠ABF ACF BPC =∠=∠∴∠,ACF BPC FEC PEC =∠∠=∠∴△FEC CEP ∆∽ ∴CE EP EF CE= 即CE 2＝EF •EP ；（2）∵四边形ABCD 是平行四边形，∴AD//BC∴△PFD PBC ∆∽ ∴FD PD BC PC= ∵D 是CP 的中点， ∴PD=12PC ∴12FD BC = ∴1122DF BC AD == 即F 为AD 的中点，F 为BP 的中点∵∠,AEB PEC ABE BPC =∠∠=∠∴△ABE CPE ∆∽ ∴12BE AB PE CP ==∴22PE BE ==⨯=∴12EF EP PF BP =-= 1()2BE EP =+==故EF =【点睛】此题考查了平行四边形的性质以及相似三角形的判定与性质，此题难度适中，注意掌握数形结合思想．23．体验：∽；探究：△ABM ∽△MCD ；拓展：DE ＝103 【分析】体验：根据同角的余角相等得到∠BAM=∠DMC ，根据平行线的性质得到∠C=∠B=90°，根据两角相等的两个三角形相似证明结论；探究：根据三角形的外角性质、相似三角形的判定定理证明；拓展：根据相似三角形的性质求出BD ，根据等腰直角三角形的性质求出AD ，根据勾股定理计算，得到答案．【详解】解：体验：∵∠AMD ＝90°，∴∠AMB +∠DMC ＝90°，∵∠B ＝90°，∴∠AMB +∠BAM ＝90°，∴∠BAM ＝∠DMC ，∵AB ∥CD ，∠B ＝90°，∴∠C ＝∠B ＝90°，∴△ABM ∽△MCD ，故答案为：∽；探究：∵∠AMC ＝∠BAM +∠B ，∠AMC ＝∠AMD +∠CMD ，∴∠BAM +∠B ＝∠AMD +∠CMD ．∵∠B ＝∠AMD ，∴∠BAM ＝∠CMD ，∵∠B ＝∠C ，∴△ABM ∽△MCD ；拓展：同探究的方法得出，△BDM ∽△CME ， ∴BD CM ＝BM CE，∵点M 是边BC 的中点，∴BM ＝CM ＝，∵CE ＝6，∴＝6， 解得，BD ＝163， ∵∠B ＝∠C ＝45°，∴∠A ＝180°﹣∠B ﹣∠C ＝90°，∴AC ＝AB ＝2BC ＝8， ∴AD ＝AB ﹣BD ＝8﹣163＝83，AE ＝AC ﹣CE ＝2，在Rt △ADE 中，DE 103． 【点睛】 本题考查的是相似三角形的判定与性质、勾股定理、三角形内角和定理以及三角形外角性质，解本题的关键是判断出△ABM ∽△MCD ．24．（1）见解析；（23）2123h h h =⋅【分析】（1）根据45PBA PBC PAB PBA ∠+∠=∠+∠=︒，利用两角分别相等的两个三角形相似即可证得结果；（2）由题意可得AB BC =1）的结论可得，AB PA BC PB=，从而即可求得PB ； （3）根据两角分别相等的两个三角形相似，可证得Rt AEP Rt CDP △△∽，求得322h h =，由PAB PBC △∽△可得32h ，从而得出结论．【详解】（1）∵90ACB ∠=︒，AC BC =，∴45ABC PBA PBC ∠=︒=∠+∠，又∵135APB ∠=︒，∴45PAB PBA ∠+∠=︒，∴PBC PAB ∠=∠，又∵135APB BPC ∠=∠=︒，∴PAB PBC △∽△；（2）由题可知，△ABC 为等腰直角三角形，∴AB BC=由（1）可知，AB PA BC PB =， ∴222BC PB PA AB ==⨯=； （3）如图，过点P 作PD BC ⊥，PE AC ⊥，PF BA ⊥，∴1PF h =，2PD h =，3PE h =，∵135135270CPB APB ∠+∠=︒+︒=︒，∴90APC ∠=︒，∴90EAP ACP ∠+∠=︒，又∵90ACB ACP PCD ∠=∠+∠=︒，∴EAP PCD ∠=∠，∴Rt Rt AEP CDP △∽△，由（1）可进一步得出，2PA PB =，2PB PC =， ∴2PA PC =，∴2PE AP DP PC==，即322h h =， ∴322h h =，∵PAB PBC △∽△，∴122h AB h BC== ∴122h h =，∴2212222322h h h h h h ==⋅=，即：2123h h h =⋅．【点睛】本题主要考查了等腰直角三角形的性质，相似三角形的判定和性质，综合性较强，有一定的难度．25．（1）画图见解析；1(2,1)C -；（2）画图见解析；2(4,2)C -．【分析】（1）根据题意得到A ，B ，C 关于原点O 的对称点连接即可；（2）根据位似图形的作图方法作图即可；【详解】解：（1）根据题意可得()11,3A -，()12,3B ，()12,1C -，如图，1(2,1)C -， （2）根据题意可得，()22,6A -，()24,6B ，()24,2C -连接即可，如图，2(4,2)C -．【点睛】本题主要考查了旋转变换和位似变换，准确作图是解题的关键．26．见解析，11(),(2,6)8,2B C【分析】根据点A 、1A 的坐标求出位似比为2：1，再利用位似图形的性质得出对应点的位置即可得出答案．【详解】111A B C △与ABC 是以坐标原点О为位似中心的位似图形，点A 坐标为()2,1，点1A 的坐标为()4,2∴111A B C △与ABC 的位似比为2：1∴如图所示：111A B C △即为所求；11(),(2,6)8,2B C .【点睛】本题考查了位似三角形的性质，在直角坐标系中作位似图形，解题关键是熟练掌握位似的性质．。

第3章图形的相似【经典例题】1.（2014湖北咸宁，6，3分）如图，正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为1∶2，点A 的坐标为(1，0)，则E点的坐标为（）．A ．(2，0)B ．(23，23)C ．(2，2)D ．(2，2)【解析】由已知得，E 点的坐标就是点A 坐标的2倍．【答案】C【点评】本题着重考查了位似图形的坐标特点，注意本题是同向位似．2.(2014山东日照，8，3分)在菱形ABCD 中，E 是BC 边上的点，连接AE 交BD 于点F, 若EC =2BE ,则FDBF的值是（ ） A.21 B.31 C.41 D.51 解析：如图，由菱形ABCD 得AD ∥BE,，所以△BEF ∽△ADF, 又由EC =2BE ,得AD=BC=3BE ,故FD BF =AD BE =31. 解答：选B ．点评：本题主要考查了棱形的性质、相似三角形的判定与性质，正确画出图形是解题的关键.3.（2014·湖南省张家界市·10题·3分）已知ABC △与DEF △相似且面积比为4∶25，则ABC △与DEF △的相似比为 ．【分析】相似三角形相似比等于面积比的算术平方根.【解答】ABC △与DEF △的相似比为254=52. 【点评】相似三角形面积比等于相似比的平方.4.（2014山东省滨州，18，4分）如图，锐角三角形ABC 的边AB ，AC 上的高线CE 和BF 相交于点D ，请写出图中的两对相似三角形： （用相似符号连接）．【解析】（１）由于∠BDE=∠CDF ∠BED=∠CFD=90°，可得△BDE ∽△CDF 。

由于∠A=∠A ，∠AFB=∠AEC=90°，可得△ABF ∽△ACE 。

解：（1）在△BDE 和△CDF 中∠BDE=∠CDF ∠BED=∠CFD=90°，∴△BDE ∽△CDF ． （2）在△ABF 和△ACE 中，∵∠A=∠A ，∠AFB=∠AEC=90°，∴△ABF ∽△ACE ． 【答案】△BDE ∽△CDF ，△ABF ∽△ACEA B CDF E（第6题）y xAOCBD EF【点评】本题考查相似三角形的判定方法．三角形相似的判定方法有，AA ，AAS 、ASA 、SAS 等．5.(2014贵州黔西南州，17，3分)如图5，在梯形ABCD 中，AD ∥BC ，对角线AC 、BD 相交于点O ，若AD=1，BC=3，△AOD 的面积为3，则△BOC 的面积为___________．【解析】由题意知AD ∥BC ，所以∠OAD=∠OCB ，∠ODA=∠OBC ，所以△OAD ∽△OCB ．又AD=1，BC=3，所以△OAD 与△OCB 的相似比为1:3，面积之比为1:9，而△AOD 的面积为3，所以△BOC 的面积为27． 【答案】27．【点评】理解相似三角形的相似比与周长比、面积比之间的关系，是解决本题的关键．6.（2014贵州遵义，7,3分）如图，在△ABC 中，EF∥BC，=，S 四边形BCFE =8，则S △ABC =（ ）A ． 9B ． 10C ． 12D ． 13解析：求出的值，推出△AEF∽△ABC，得出=，把S 四边形BCFE =8代入求出即可．解：∵=， ∴==，∵EF∥BC，∴△AEF∽△ABC， ∴==，∴9S △AEF =S △ABC ， ∵S 四边形BCFE =8，∴9（S △ABC ﹣8）=S △ABC ， 解得：S △ABC =9． 故选A ．答案： A点评： 本题考查了相似三角形的性质和判定的应用，注意：相似三角形的面积比等于相似比的平方，题型较好，但是一道比较容易出错的题目．7.（2014南京市，15，2）如图，在平行四边形ABCD 中，AD=10厘米，CD=6厘米，E 为AD 上一点，且BE=BC,CE=CD ，则DE= 厘米.CAE解析：△BCE 与△CDE 均为等腰三角形，且两个底角∠DEC=∠BCE ，∴△BCE ∽△CDE ，∴CD BC =DECE,∴610=DE6,∴DE=3.6厘米. 答案：3.6.点评：在图形中，利用相似，得出比例式，可以求出线段的长.8.(2014山东日照，21，9分) 如图，在正方形ABCD 中，E 是BC 上的一点,连结AE ，作BF ⊥AE ，垂足为H ,交CD 于F ,作CG ∥AE ,交BF 于G .(1)求证CG =BH ; (2)FC 2=BF·GF ;(3) 22AB FC =GBGF .解析：(1)可证△ABH ≌△BCG ；(2)证△CFG ∽△BFC 可得；(3)先证△B CG ∽△BFC 得BC 2=BF·BG ,结合AB=BC 可得. 证明： （1）∵BF ⊥AE ，CG ∥AE , CG ⊥BF , ∴ CG ⊥BF .∵在正方形ABCD 中，∠ABH+∠CBG =90o, ∠CBG+∠BCG =90o,∠BAH+∠ABH =90o,∴∠BAH=∠CBG, ∠ABH=∠BCG,AB=BC,∴△ABH ≌△BCG , ∴CG=BH ;(2) ∵∠BFC=∠CFG, ∠BCF=∠CGF=90 o,∴△CFG ∽△BFC , ∴FCGFBF FC =, 即FC 2=BF ·GF ;(3) 由（2）可知，BC 2=BG ·BF , ∵AB=BC ,∴AB 2=BG ·BF ,∴22BC FC =BF BG BF FG ••=BGFGAF即22AB FC =GBGF 点评：本题考查了正方形的性质、全等三角形和相似三角形的判定与性质，解题的关键是找到全等（或相似）三角形，并找到三角形全等（或相似）的条件.9.(2014海南省，12，3分）12、如图3，在△ABC 中，∠ACB=090，CD ⊥AB ，于点D ，则图中相似三角形共有（ ）CDBAA 、1对B 、2对C 、3对D 、4对【解题思路】由射影定理可知图中相似三角形共有三对：△BDC ～△BCA ～△CDA 【答案】C ．【点评】本题主要考查相似三角形基本图形中的一种，也是很重要的一种：射影定理。

九年级数学中考《图形的相似》专项训练题（A）1．如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O，那么点B′位似，且矩形OA′B′C′的面积等于矩形OABC面积的14的坐标是（）．A．（3，2） B．（－2，－3）C．（2，3）或（－2，－3） D．（3，2）或（－3，－2）2. 如图，△ABC中，BC=2，DE是它的中位线，下面三个结论：⑴DE=1；⑵△ADE∽△ABC；⑶△ADE的面积与△ABC的面积之比为1:4。

其中正确的有（）．A. 0个B.1个C. 2个D. 3个3．如图，四边形ABCD的对角线AC、BD相交于O，且将这个四边形分成①、②、③、④四个三角形．OA∶OC=OB∶OD，则下列结论中一定正确的是( )．A ．①和②相似B ．①和③相似C ．①和④相似D ．②和④相似4．现给出下列四个命题：①无公共点的两圆必外离；②位似三角形是相似三角形；③菱形的面积等于两条对角线的积；④对角线相等的四边形是矩形．其中真命题的个数是（ ）．A ．1B ．2C ．3D ．45．如图，线段AB 两个端点的坐标分别为A （4，4），B （6，2），以原点O 为位似中心，在第一象限内将线段AB 缩小为原来的后得到线段CD ，则端点C 和D 的坐标分别为（ ）A ．（2，2），（3，2）B ．（2，4），（3，1）C ．（2，2），（3，1）D ．（3，1），（2，2）6．如图，在平行四边形ABCD 中（AB ≠BC ），直线EF 经过其对角线的交点O ，且分别交AD 、BC 于点M 、N ，交BA 、DC 的延长线于点E 、F ，下列结论：①AO=BO ；②OE=OF ；③△EAM ∽△EBN ；④△EAO ≌△CNO ，其中正确的是（ ）． A ．①② B ．②③ C ．②④ D ．③④AB CD O ① ②⊙o ③⊙o④⊙o7.下列图形中不是位似图形的是( ).8.在比例尺1：10 000 000的地图上，量得甲、乙两个城市之间的距离是8 cm，那么甲、乙两个城市之间的实际距离应为 __________km.9. 如果一个三角形的三边长为5、12、13，与其相似的三角形的最长的边为39，那么较大的三角形的周长________，面积________．10.如图，为了测量某棵树的高度，小明用长为2m的竹竿做测量工具，移动竹竿，使竹竿、树的顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距6m、与树相距15m，则树的高度为______________m11. 如图，以点O为位似中心，将五边形ABCDE放大后得到五边形A′B′C′D′E′，已知OA=10cm，OA′=20cm，则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是________．12. 将三角形纸片（△ABC）按如图所示的方式折叠，使点B落在边10 98 7 6 5 4 3 2 1 11 A 1 B 1 C 1 A B Cy AC 上，记为点B ′，折痕为EF ．已知AB ＝AC ＝6，BC ＝8，若以点B ′，F ，C 为顶点的三角形与△ABC 相似，那么BF 的长度是________．13.如图，在△ABC 中，∠BAC=60°，∠ABC=90°，直线l 1∥l 2∥l 3，l 1与l 2之间距离是1，l 2与l 3之间距离是2，且l 1，l 2，l 3分别经过点A ，B ，C ，则边AC 的长为．14. 如图，不等长的两条对角线AC 、BD 相交于点O ，且将四边形ABCD 分成甲、乙、丙、丁四个三角形．若12AO BO OC OD ==，则甲、乙、丙、丁这4个三角形中，一定相似的有________．15 . 如图，已知图中的每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点．若△ABC 与△A 1B 1C 1是位似图形，且顶点都在格点上，则位似中心的坐标是___________．16．如图，一个矩形ABCD 的长AD=a cm，宽AB=b cm，E、F分别是AD、BC的中点，连接E、F，所得新矩形ABFE与原矩形ABCD相似，求a:b的值．17．如图，△ABC是一块直角三角形的木块，∠C=90°，AC=3cm，BC=4cm，AB=5cm，要利用它加工成一块面积最大的正方形木块，问按正方形CDEF加工还是按正方形PQRS加工？说出你的理由.18.已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点.若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？19. 如图，已知在△ABC中AB=AC，点D为BC边的中点，点F在边AB上，点E在线段DF的延长线上，且∠BAE=∠BDF，点M在线段DF 上，且∠EBM=∠C．（1）求证：EB•BD=BM•AB；（2）求证：AE ⊥BE ．20. 已知线段OA ⊥OB ，C 为OB 上中点，D 为AO 上一点，连AC 、BD 交于P 点．（1）如图1，当OA=OB 且D 为AO 中点时，求PC AP 的值； （2）如图2，当OA=OB ，AO AD =41时，求tan ∠BPC ；21.已知：如图，在△ABC 中，点D 、E 分别在边BC 、AB 上，BD=AD=AC ，AD 与CE 相交于点F ，AE 2=EF •EC ．（1）求证：∠ADC=∠DCE+∠EAF ；（2）求证：AF •AD=AB •EF ．DC P O A B 图 1D C POAB 图 222．如图，在矩形ABCD中，E为CD的中点，F为BE上的一点，连结CF并延长交AB于点M，MN⊥CM交射线AD于点N．（1）当F为BE中点时，求证：AM=CE；（2）若==2，求的值；（3）若==n，当n为何值时，MN∥BE？23．如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB 于点D.(1)尺规作图：过A，D，C三点作⊙O（只要求作出图形，保留痕迹，不要求写作法）；(2)求证：BC是过A，D，C三点的圆的切线；(3)若过A，D，C三点的圆的半径为3,则线段BC上是否存在一点P，使得以P，D，B为顶点的三角形与△BCO相似.若存在，求出DP的长；若不存在，请说明理由.CBA24.如图，在矩形ABCD中，AB=4，AD=10，直角尺的直角顶点P在AD 上滑动时（•点P与A，D不重合），一直角边经过点C，另一直角边交AB于点E．我们知道，结论“Rt•△AEP∽Rt△DPC”成立．（1）当∠CPD=30°时，求AE的长；（2）是否存在这样的点P，使△DPC的周长等于△AEP周长的2倍？若存在，求出DP的长；若不存在，请说明理由．。

一、选择题1．如图，在ABC 中，D ，E 分别是AB,AC 上的点，且DE// BC ，若AE ： EC=1： 4，那么:ADE BEC S S △△的值为（ ）A ．1∶16B ．1∶18C ．1∶20D ．1∶24 2．如图，在▱ABCD 中，E 是BC 的中点，DE ，AC 相交于点F ，S △CEF ＝1，则S △ADC ＝（ ）A ．3B ．4C ．5D ．63．如图，在▱ABCD 中，点O 是对角线BD 上的一点，且12OD OB =，连接CO 并延长交AD 于点E ，若△COD 的面积是2，则四边形ABOE 的面积是（ ）A ．3B ．4C ．5D ．64．已知小亮的身高为1.8米，同一时刻，小亮在阳光下的影长为2米，与他邻近的旗杆的影长为6米，则旗杆的高为（ ）．A ．3.8米B ．5.4米C ．5.6米D ．6米5．下列说法中，正确的说法有（ ）①对角线互相平分且相等的四边形是菱形；②一元二次方程2340x x --=的根是14x =，21x =-；③两个相似三角形的周长的比为23，则它们的面积的比为49； ④对角线互相垂直的平行四边形为正方形；⑤对角线垂直的四边形各边中点得到的四边形是矩形． A ．1个 B ．2个 C ．3个 D ．4个6．如图，直线123////l l l ，则（ ）A．AD EBEB FC=B．AB DEAC EF=C．BC DEAC DF=D．AB DEBC EF=7．如图，在△ABC中，点D，E分别在边AB、AC上，下列条件中不能判断△ABC∽△ADE 的是（）A．∠ADE＝∠B B．∠AED＝∠C C．AD ABAE AC=D．DE AEBC AC=8．古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点G 将一线段MN分为两线段MG、GN，使得其中较长的一段MG是全长MN与较短的一段GN的比例中项，即满足512MG GNMN MG-==，后人把512-这个数称为“黄金分割数”，把点G称为线段MN的“黄金分割点”．如图，在△ABC中，已知AB＝AC＝3，BC＝4，若点D是边BC边上的一个“黄金分割点”，则△ADC的面积为（）A．55B．355C．205-D．1045-9．如图，在ABC中，中线BE，CD相交于点O，连接DE，给出下列结论∶①12DEBC=；②12SS=△DOE△COB；③AD OEAB OB=；④13COEADCSS=△△；⑤23BDOBCOSS=△△．其中不正确的个数是（）A ．1B ．2C ．3D ．410．已知等腰△ABC 的底角为75°，则下列三角形一定与△ABC 相似的是（ ） A ．顶角为30°的等腰三角形B ．顶角为40°的等腰三角形C ．等边三角形D ．顶角为75°的等腰三角形11． OAB 在平面直角坐标系中的位置如图所示，已知点A 的坐标为()3,33，OAB 与OA B ''△关于点О成位似图形，且在点О的同一侧，OAB 与OA B ''△的位似比为1：2，则点A 的对应点A '的坐标是（ ）A ．()6,63-B ．()6,63-C ．()3,33--D ．()6,63 12．如图，在平行四边形ABCD 中，对角线AC ，BD 交于点O ，M 为AD 中点，连接CM ，交BD 于点N ，则:CNO CND S S ∆∆=（ ）A ．1:2B ．2:3C ．1:3D ．3:4二、填空题13．如图，为测量学校围墙外直立电线杆AB 的高度，小红在操场上点C 处直立高3m 的竹竿CD ，然后退到点E 处，此时恰好看到竹竿顶端D 与电线杆顶端B 重合；小红又在点1C 处直立高3m 的竹竿11C D ，然后退到点1E 处，此时恰好看到竹竿顶端1D 与电线杆顶端B 重合．小红的眼睛离地面高度 1.5EF m =，量得2CE m =，18EC m =，114C E m =，则电线杆AB 的高度为______m ．14．如图，平面直角坐标系中，点(0,2),(4,0)A B ，将ABO 沿着垂直于x 轴的直线CD 折叠（点C 在x 轴上，点D 在AB 上，点D 不与A ，B 重合），点B 的对应点为点E ，则当ADE为直角三角形时BDC ADES S 的值是_____________．15．如图，直线122y x =-+与坐标轴分别交于点,A B ，与直线12y x =交于点,C Q 是线段OA 上的动点，连接CQ ，若OQ CQ =，则点Q 的坐标为___________．16．如图，正方形ABCD 中，点F 在边AB 上，且AF ：FB ＝1：2，AC 与DF 交于点N ．（1）当AB ＝4时，AN ＝_____．（2）S △ANF ：S 四边形CNFB ＝_____．（S 表示面积）17．如图，小明在A 时测得某树的影长为1.5m ，B 时又测得该树的影长为6m ，若两次日照的光线互相垂直，则树的高度为__________m ．18．给出下列说法：①对角线相等的平行四边形是矩形；②一条线段只有两个黄金分割点；③两根长度不同的木棍，在同一盏路灯下同一时刻的影子有可能一样长；④所有六边形都相似，其中正确的是_____．（填序号）19．如图，在ABC 中，AB AC >，将ABC 以点A 为中心顺时针旋转，得到AED ，点D 在BC 上，DE 交AB 于点F ．如下结论中：①DA 平分EDC ∠；②AEF DBF △∽△；③BDF CAD ∠=∠；④EF BD =．所有正确结论的序号是_____．20．如图，在ABC 中，////DE FG BC ，ADE 的面积＝梯形DFGE 的面积＝梯形FBCG 的面积，则DE BC的值为______．三、解答题21．如图，直角坐标系xOy 中，一次函数+6y x =-的图象1l 分别与,x y 轴交于,A B 两点，正比例函数的图象2l 与1l 交于点(),5C m（1）求m 的值及2l 的解析式；（2）求AOC S 的值；（3）垂直于x 轴的直线x a =与直线12,l l 分别交于点,P Q ，若线段2PQ =，求a 的值； （4）一次函数64y kx k =-+的图象与线段AB （含端点）有公共点，且满足y 随x 的增大而减小，设直线与x 轴的交点横坐标为,x 直接写出x 的取值范围．22．如图，正方形ABCD 中，P 是BC 上一点（点P 不与点B ，C 重合），连接AP ，作⊥PE AP ，PE 交CD 于点E ．（1）求证：PEC APB ∽△△；（2）若6AB =，点P 为BC 的中点，求DE 的长．23．如图，F 为四边形ABCD 边CD 上一点，连接AF 并延长交BC 延长线于点E ，已知D DCE ∠=∠．（1）求证：ADF ECF ∽△△；（2）若ABCD 为平行四边形，6AB =，2EF AF =，求FD 的长度．24．如图，在△ABC 中，点D ，E ，F 分别在AB ，BC ，AC 边上，DE ∥AC ，EF ∥AB ．（1）求证：△BDE ∽△EFC ；（2）设12AF FC =． ①若BC ＝20，求线段BE 的长；②若△EFC 的面积是36，求△ABC 的面积．25．如图1，在平面直角坐标系O x y 中，抛物线223y x bx c =-++与x 轴交于A 、B 两点，其中()6,0B ，与y 轴交于点()0,8C ，点P 是x 轴上方的抛物线上一动点（不与点C（1）求抛物线的表达式；（2）过点P 作PD x ⊥轴于点D ，交直线BC 于点E ，点E 关于直线PC 的对称点为E '，若点E '落在y 轴上（不与点C 重合）．请判断以P ，C ，E ，E '为顶点的四边形的形状，并说明理由；（3）在（2）的条件下直接写出点P 的坐标．26．如图，在平面直角坐标系中，ABC 的三个顶点坐标分别为(1,3),(2,3),(2,1)A B C ----．（1）画出ABC 关于原点O 成中心对称的111A B C △，并写出点1C 的坐标； （2）以原点O 为位似中心，在x 轴上方画出ABC 放大2倍后的222A B C △，并直接写出点2C 的坐标．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C由已知条件可求得ABE EBC S S ∆∆，又由平行线分线段成比例可求得ADE BDES S ∆∆，结合S △BDE =S △ABE -S △ADE 可求得答案．【详解】解：∵AE 1EC 4=， ∴14ABE EBC S S ∆∆=， ∴14ABE EBC S S ∆∆=， ∵DE ∥BC ， ∴14AD AE DB EC ==， ∴14ADE BDE S S ∆∆=， ∴S △BDE =4S △ADE ，又∵S △BDE =S △ABE -S △ADE ，∴4S △ADE =14S △EBC -S △ADE ， ∴120ADE EBC S S ∆∆=， 故选：C ．【点睛】本题主要考查了平行线分线段成比例的性质及三角形的面积，掌握同高三角形的面积比即为底的比是解题的关键．2．D解析：D【分析】根据已知可得△CEF ∽△ADF ，及EF 和DF 的关系，从而根据相似三角形的性质和三角形的面积得到答案．【详解】解：∵四边形ABCD 是平行四边形∴AD=BC ，△CEF ∽△ADF ， ∴EC EF AD DF= ∵E 是BC 的中点，∴EC=1122BC AD =∴12EC EF AD DF == ∴2211()()24CEF ADF S EF S DF ∆∆=== ∵S △CEF ＝1，∴S △ADF ＝4， ∵12EF DF = ∴DF=2EF ∴S △D CF ＝2 S △CEF ＝2，∴S △ADC ＝S △ADF + S △D CF =4+2=6故选：D ．【点睛】本题主要考查了相似三角形的判定与性质，熟练掌握相似三角形的面积比等于相似比的平方是解答此题的关键．3．C解析：C【分析】由题意可得△BOC 的面积为4，通过证明△DOE ∽△BOC ，可求S △DOE ＝1，即可求解．【详解】解：∵12OD OB =，△COD 的面积是2， ∴△BOC 的面积为4，∵四边形ABCD 是平行四边形，∴AD ∥BC ，S △ABD ＝S △BCD ＝2＋4＝6，∴△DOE ∽△BOC ， ∴DOE BOC S S .（OD OB ）2＝14， ∴S △DOE ＝1，∴四边形ABOE 的面积＝6﹣1＝5，故选：C ．【点睛】本题主要考查了相似三角形的判定与性质，准确计算是解题的关键．4．B解析：B【分析】设旗杆的高度约为hm ，再根据同一时刻物高与影长成正比求出h 的值即可．【详解】解：设旗杆的高度约为hm ，∵同一时刻物高与影长成正比， ∴1.826h =， 解得：h ＝5.4（米）．故选：B ．【点睛】本题考查的是相似三角形的应用，熟知同一时刻物高与影长成正比是解答此题的关键． 5．C解析：C【分析】根据矩形的判定定理、一元二次方程的解法、【详解】解：①对角线互相平分且相等的四边形是矩形，故①错误；②一元二次方程x 2-3x -4=0（x -4）（x +1）=0x -4=0或x =1=0x 1=4，x 2=-1，故②正确；③两个相似三角形的周长的比为23，则它们的面积的比为22()349=，故③正确； ④对角线相等且互相垂直的平行四边形为正方形，故④错误；⑤对角线垂直的四边形各边中点得到的四边形是矩形，说法正确．故选：C【点睛】 本题考查的是命题的真假判断，掌握矩形的判定定理、一元二次方程的解法、中点四边形的性质、矩形、菱形和正方形的判断是解题的关键．6．D解析：D【分析】根据平行线分线段成比例，依次对各选项进行判断即可．【详解】解：∵123////l l l ， ∴AB DE AC DF=，B 选项错误，不符合题意； BC EF AC DF=，C 选项错误，不符合题意； AB DE BC EF=，D 选项正确，符合题意； 无法确定A 选项是否正确，故A 选项不符合题意；故选：D ．【点睛】本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例． 7．D解析：D【分析】根据相似三角形的判定定理对各选项进行逐一判断即可．【详解】解：A 、∠ADE=∠B ，∠A=∠A ，则可判断△ABC ∽△ADE ，故A 选项不符合题意； B 、∠AED=∠C ，∠A=∠A ，则可判断△ABC ∽△ADE ，故B 选项不符合题意；C 、AD AB AE AC =，即AD AE AB AC=，且夹角∠A=∠A ，则可判断△ABC ∽△ADE ，故C 选项不符合题意； D 、DE AE BC AC=，缺少条件∠AED 和∠ACB 相等，则不能确定△ABC ∽△ADE ，故D 选项符合题意；故选：D ．【点睛】本题考查的是相似三角形的判定，熟知相似三角形的判定定理是解答此题的关键． 8．A解析：A【分析】作AF ⊥BC ，根据等腰三角形ABC 的性质求出AF 的长，再根据黄金分割点的定义求出CD 的长度，利用三角形面积公式即可解题．【详解】解：过点A 作AF ⊥BC ，∵AB=AC ，∴BF=12BC=2，在Rt ABF ，==∵D 是边BC 的两个“黄金分割”点，∴CD BC =即4CD =，解得CD=2，∴12ADC C AF S D ⨯⨯==()122⨯5， 故选：A ．【点睛】本题考查了“黄金分割比”的定义、等腰三角形的性质、勾股定理的应用以及三角形的面积公式，求出DC 和AF 的长是解题的关键．9．B解析：B【分析】根据中位线的性质，//DE BC ，通过证明DOE COB △∽△，得DOE COB S S；根据相似三角形性质，通过证明ADE ABC △△∽，证得AD OE AB OB=；结合点D 是AB 的中点，点E 是AC 的中点，通过三角形面积关系计算，即可得到COE ADC S S △△，同理计算得BDO BCO S S △△，即可得到答案．【详解】根据题意得：点D 是AB 的中点，点E 是AC 的中点 ∴DE 是ABC 的中位线∴12DE BC =，即①结论正确； 又∵DE 是ABC 的中位线 ∴//DE BC∴DEO CBO ∠=∠，EDO BCO ∠=∠∴DOE COB △∽△ ∴12OE OD DE OB OC BC ===，214DOE COB S DE SBC ⎛⎫== ⎪⎝⎭，即②结论错误； 又∵//DE BC ∴ADE ABC =∠∠，AED ACB ∠=∠∴ADE ABC △△∽ ∴12AD DE AB BC == ∴AD OE AB OB =，即③结论正确；∵12OE OB = ∴13OE OE BE OB OE ==+ ∴13COE BEC S OE S BE ==△△ ∵点D 是AB 的中点，点E 是AC 的中点 ∴12ADC ABC S AD S AB ==△△，12BEC ABC S CE S AC ==△△ ∴111326COE COE BEC ABC BEC ABC S S S S S S =⨯=⨯=△△△△△△ ∴1632COE COEABC ADC S S S S ==△△△△，即④结论正确； ∵12OD DE OC BC == ∴12BDO BCO S OD S OC ==△△，即⑤结论错误； 故选：B ．【点睛】本题考查了三角形中位线、相似三角形、平行线的知识；解题的关键是熟练掌握三角形中位线、相似三角形的性质，从而完成求解．10．A解析：A【分析】根据等腰三角形的性质得出等腰三角形的角的度数，进而利用相似三角形的判定解答即可．【详解】解：∵等腰△ABC 的底角为75°，∴等腰△ABC 的三角的度数分别为30°，75°，75°∴一定与△ABC 相似的是顶角为30°的等腰三角形故选：A ．【点睛】本题考查了想做浅咖人判定，关键是根据等腰三角形的性质得出等腰三角形的角的度数解答．11．D解析：D【分析】根据位似图形的性质和△OAB 和△OA B ''的位似比为1:2，即可求出两三角形的相似比为1:2，即可根据点A 的坐标求出点A '的坐标；【详解】如图所示：作AC ⊥OB 于点C ，∵A(3，33，AC ⊥OB ，∴ OC=3， AC=33∴ 229276OA OC AC =+=+=，∵ △AOB 和△OA B ''的位似比为1:2，∴ OA '=2OA=12，即△AOB 和△OA B ''的相似比为1:2，∴ A '(6，3，故选：D ．【点睛】本题主要考查了相似图形与位似图形的性质，正确理解位似图形是解题的关键． 12．A解析：A【分析】由四边形ABCD 为平行四边形，得到对边平行，即可证得：△BCN ∽△DMN ；可求相似比为2:1，继而求出ON:DN ，从而可求:CNO CND S S ∆∆．【详解】解：∵四边形ABCD 是平行四边形，M 为AD 中点，∴AD ∥BC ，BC=AD=2 DM ，OB=OD ，∴∠BCN=∠DMN ，∠NBC=∠MDN ，∴△BCN ∽△DMN ；∴BN:DN=BC:DM=2:1，设DN=x ，则BN =2x ，∴BD=3x ，∴OD=32x ，∴ON=12x ， ∴ON:DN=12x: x =1:2， ∴:CNO CND S S ∆∆= ON:DN =1:2．故选：A ．【点睛】此题考查了相似三角形的判定与性质以及平行四边形的性质．要掌握等高三角形面积的比等于其对应底边的比．二、填空题13．5【分析】利用相似三角形的对应边成比例可得相关的两个比例式求得BG 的长加上15即为AB 的高【详解】解：∵DC ⊥AE ⊥AEBA ⊥AE ∴DC ∥∥BA ∴∴∵DC ∥BA ∴△FDM ∽△FBG ∴∵N=DM ∴即∴解析：5【分析】利用相似三角形的对应边成比例可得相关的两个比例式，求得BG 的长，加上1.5即为AB 的高．【详解】解：∵DC ⊥AE ，11D C ⊥AE ，BA ⊥AE ，∴DC ∥11D C ∥BA ，∴111F D N F BG ∽, ∴111D N F N BG F G=． ∵DC ∥BA ，∴△FDM ∽△FBG ． ∴DM FM BG FG=． ∵1D N=DM ， ∴11F N FM F G FG =，即 42142GM GM =++． ∴GM=10m ． ∵111D N F N BG F G=， ∴1.5424BG =．∴BG=9m ．∴AB=BG+GA=10.5（m ）．故答案是：10.5．【点睛】本题考查相似三角形的应用；解这道题的关键是将实际问题转化为数学问题，本题只要把实际问题抽象到相似三角形中，利用相似比列出方程即可求出．14．或【分析】分两种情况：当是以点E 为直角顶点时和当是以点A 为直角顶点时分别利用相似三角形的判定及性质求解即可【详解】①当是以点E 为直角顶点时∵将沿着垂直于x 轴的直线折叠（点C 在x 轴上点D 在上点D 不与A 解析：310或56【分析】 分两种情况：当ADE 是以点E 为直角顶点时和当ADE 是以点A 为直角顶点时，分别利用相似三角形的判定及性质求解即可．【详解】①当ADE 是以点E 为直角顶点时，(0,2),(4,0)A B ，2,4OA OB ∴==，2225AB OA OB ∴=+=∵将ABO 沿着垂直于x 轴的直线CD 折叠（点C 在x 轴上，点D 在AB 上，点D 不与A ，B 重合），点B 的对应点为点E ，,,BD DE BC EC DBC DEC ∴==∠=∠，90,90AEO DEB AEO OAE ∠+∠=︒∠+∠=︒，DEB AOE ∴∠=∠，DBO OAE ∴∠=∠．又90AOB EOA ∠=∠=︒，AOE BOA ∴△△，12AO OE BO AO ∴==， 1OE ∴=， 22135,3,22AE AO OE BE OB OE BC BE ∴=+==-===．1tan 2AO DC ABO OB CB ∠===， 34DC ∴=， 2235BD DE BC CD ∴==+=， 11339113515,5224216228BDC ADE S DC BC S AE DE ∴=⋅=⨯⨯==⋅=⨯⨯=△△， 931615108BDCADE SS ∴==； ②当ADE 是以点A 为直角顶点时，90,90AEO EAO AEO ABO ∠+∠=︒∠+∠=︒，EAO ABO ∴∠=∠．又90AOB EOA ∠=∠=︒， AOE BOA ∴△△，12AO OE BO AO ∴==， 1OE ∴=， 22155,5,22AE AO OE BE OB OE BC BE ∴=+==+===． 1tan 2AO DC ABO OB CB ∠===， 54DC ∴=， 2255BD BC CD ∴=+=， 35AD AB BD ∴=-=， 115525113515,52224162248BDC ADE S DC BC S AD DE ∴=⋅=⨯⨯==⋅=⨯=△△，255161568BDC ADE SS ∴==， 综上所述，BDC ADE S S 为310或56． 故答案为：310或56． 【点睛】 本题主要考查相似三角形的判定及性质，掌握相似三角形的判定及性质并分情况讨论是解题的关键．15．【分析】与联立组成方程组求出点C 的坐标为（21）从而可判断点C 是AB 的中点所以OC=AC 从而得到∠AOC=∠OAC 又因为所以∠AOC=∠OCQ 从而可判断△OCQ ∽△OAC 再根据相似三角形的性质可得最解析：5,04⎛⎫ ⎪⎝⎭【分析】122y x =-+与12y x =联立组成方程组求出点C 的坐标为（2，1）从而可判断点C 是AB 的中点，所以OC=AC ，从而得到∠AOC=∠OAC ，又因为OQ CQ =，所以∠AOC=∠OCQ ，从而可判断△OCQ ∽△OAC ，再根据相似三角形的性质可得OQ OC OC OA =，最后把数值代入求出OQ 的长，从而得到Q 点的坐标．【详解】解：如图所示，依题意得：12212y x y x ⎧=-+⎪⎪⎨⎪=⎪⎩解得：21x y =⎧⎨=⎩ ∴点C 的坐标为（2，1）对于直线122y x =-+，令x=0，解得y=2， 令y=0，解得x=4．∴点A ，B 的坐标分别为（4，0），（0，2）．∴点C 是AB 的中点．∵△OAB 为直角三角形，∴OC=AC ，∴∠AOC=∠OAC ，∵OQ CQ=，∴∠AOC=∠OCQ，∴∠AOC=∠OCQ=∠OAC，∴△OCQ∽△OAC，∴OQ OCOC OA=又∵△OAB为直角三角形，OA=4，OB=2，∴222224AB OB OA=+=+=25∴OC=AC=12AB=5∴55=，解得：OQ=54，∴点Q的坐标为（54，0）．故答案为：（54，0）．【点睛】本题考查了一次函数与二元一次方程，等腰三角形的性质及相似三角形的判定和性质，掌握相关知识是解题的关键．16．1∶11【分析】（1）利用平行线分线段成比例定理等腰直角三角形的性质解决问题即可（2）设△ANF的面积为m由AF∥CD推出△AFN∽△CDN推出△ADN的面积为3m△DCN的面积为9m推出△ADC的2 1∶11【分析】（1）利用平行线分线段成比例定理，等腰直角三角形的性质解决问题即可．（2）设△ANF的面积为m，由AF∥CD，推出13AF FNCD DN==，△AFN∽△CDN，推出△ADN的面积为3m，△DCN的面积为9m，推出△ADC的面积＝△ABC的面积＝12m，由此即可得S四边形CNFB=11m，即可得出答案．【详解】解：∵四边形ABCD 是正方形，∴AB ∥CD ，AB=CD ∴AF AN CD CN=， ∵AF ：FB ＝1：2，∴AF ：AB ＝AF ：CD ＝1：3， ∴13AN CN =， ∴14AN AC =， ∵AC=， ∴14=，∴AN 4=AB ； ∵AB=4∴；（2）设△ANF 的面积为m ，∵AF ∥CD ， ∴13AF FN CD DN ==，△AFN ∽△CDN ， ∴△AFN 和△CDN 高的比=13 ∴△AFN 和△ADN 高的比=13∴△ADN 的面积为3m ，△DCN 的面积为9m ，∴△ADC 的面积＝△ABC 的面积＝12m ，∴S △ANF ：S 四边形CNFB ＝1：11，【点睛】本题考查正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，学会利用参数解决问题．17．3【分析】根据题意画出示意图根据相似三角形的性质求解即可；【详解】根据题意做出示意图则∵∴∴∵∴∴∴∴∴即树的高度为3m 故答案是3【点睛】本题主要考查了相似三角形的应用和平行投影的知识点准确分析计算 解析：3【分析】根据题意画出示意图，根据相似三角形的性质求解即可；【详解】根据题意做出示意图，则CD EF ⊥，EC CF ⊥，DE 1.5m =，6DF m =，∵CD EF ⊥，∴90EDC CDF ∠=∠=︒，∴90E ECD ∠+∠=︒，∵90ECD DCF ∠+∠=︒，∴E DCF ∠=∠，∴△△EDC CDF ， ∴ED DC DC FD =， ∴29DC ED FD ==，∴3DC m =，即树的高度为3m ．故答案是3．【点睛】本题主要考查了相似三角形的应用和平行投影的知识点，准确分析计算是解题的关键． 18．①②③【分析】根据矩形的判定黄金分割点的定义相似图形的性质判断命题的正确性【详解】对角线相等的平行四边形是矩形是矩形的判定之一故①正确；如图则点C 和点D 是线段AB 的黄金分割点一条线段只有两个黄金分割 解析：①②③【分析】根据矩形的判定，黄金分割点的定义，相似图形的性质判断命题的正确性．【详解】对角线相等的平行四边形是矩形是矩形的判定之一，故①正确；如图，51AD BC AB AB -==，则点C 和点D 是线段AB 的黄金分割点，一条线段只有两个黄金分割点，故②正确；如图，CG DH ≠，但是EG HF =，两根长度不同的木棍，在同一盏路灯下同一时刻的影子有可能一样长，故③正确；并不是所有六边形都相似，故④错误．故答案是：①②③．【点睛】本题考查矩形的判定，黄金分割点的定义，相似图形的性质，解题的关键是掌握这些知识点．19．①②③【分析】由旋转性质得AD=AC∠ADE=∠C利用AD=AC得到∠ADC=∠C即可推出∠ADC=∠ADE判断①正确；根据∠E=∠B∠AFE=∠BFD即可证明△AEF∽△DBF判断②正确；利用三角解析：①②③【分析】由旋转性质得AD=AC，∠ADE=∠C，利用AD=AC得到∠ADC=∠C，即可推出∠ADC=∠ADE，判断①正确；根据∠E=∠B，∠AFE=∠BFD，即可证明△AEF∽△DBF，判断②正确；利用三角形的外角性质判断③正确；由∠FAD不一定等于∠CAD，不能证明△ADF全等于△ADC，故CD不一定等于DF，由此判断④错误．【详解】由旋转得：AD=AC，∠ADE=∠C，∵AD=AC，∴∠ADC=∠C，∴∠ADC=∠ADE，即DA平分∠EDC，故①正确；∵∠E=∠B，∠AFE=∠BFD，∴△AEF∽△DBF，故②正确；∵∠ADB=∠ADE+∠BDF=∠C+∠CAD，∠ADE=∠C，∠=∠，故③正确；∴BDF CAD∵∠FAD不一定等于∠CAD，AD=AD，∠ADC=∠ADE，∴不能证明△ADF全等于△ADC，故CD不一定等于DF，∴DE-DF不一定等于BC-CD，即无法证明EF=BD，故④错误；故答案为：①②③．【点睛】此题考查旋转的性质，等腰三角形的性质，相似三角形的判定及性质，三角形的外角性质，是一道三角形的综合题．20．【分析】由平行线可得△ADE ∽△AFG ∽△ABC 进而利用相似三角形面积比等于对应边的平方比即可得出结论【详解】解：∵S △ADE ＝S 梯形DFGE ＝S 梯形FBCG ∵DE ∥FG ∥BC ∴△ADE ∽△AFG ∽【分析】由平行线可得△ADE ∽△AFG ∽△ABC ，进而利用相似三角形面积比等于对应边的平方比，即可得出结论．【详解】解：∵S △ADE ＝S 梯形DFGE ＝S 梯形FBCG ，∵DE ∥FG ∥BC ，∴△ADE ∽△AFG ∽△ABC ， ∴13ADE ABC S S ∆=， 由于相似三角形的面积比等于对应边长的平方比，∴DE ： BC＝1． 【点睛】本题主要考查了相似三角形的判定及性质以及三角形面积比与对应边长之间的关系，能够熟练掌握并运用． 三、解答题21．（1）1m =， 5y x =；（2）15AOC S=；（3）43a =或23a =；（4）18x ≥． 【分析】（1）由一次函数+6y x =-的图象1l 过点(),5C m ，可得+65m -=求出m ，设2l 的解析式为y kx =过点C(1,5)，求出k 即可；（2） 由y=0时，+60,6x x -==，OA=6，12AOC C S OA y =⋅； （3）当x a =时，与直线1l 交于点P （,6a a -），与直线2l 交于点Q （,5a a ），PQ=()562a a --=解之即可；（4）由一次函数64=-+y kx k 的图象横过定点(6,4) ，一次函数64=-+y kx k 的图象过B （0,6），13k =-，一次函数为163y x =-+ ，与x 轴交点，当18x ≥时即可．【详解】解：（1）∵一次函数+6y x =-的图象1l 过点(),5C m ，∴+65m -=，∴1m =，设2l 的解析式为y kx =过点C ，∴k=5，∴2l 的解析式为5y x =；（2）一次函数+6y x =-与x 轴交点为A ，当y=0时，+60,6x x -==，∴OA=6， 11651522AOC C S OA y =⋅=⨯⨯=； （3）当x a =时，与直线1l 交于点P （,6a a -），与直线2l 交于点Q （,5a a ）， PQ=()56612a a a --=-=，113a -=， 113a -=±， 43a =或23a =； （4）一次函数整理得()64y k x =-+，由64x y =⎧⎨=⎩， ∴一次函数64=-+y kx k 的图象横过定点(6,4) ，A （6,0），B （0,6），一次函数64=-+y kx k 的图象过B （0,6），∴646k -+=， ∴13k =-，∴一次函数163y x =-+， ∴y=0，x=18，当18x ≥时一次函数64=-+y kx k 的图象与线段AB （含端点）有公共点且满足y 随x 的增大而减小．【点睛】本题考查直线解析式，三角形面积，两直线l 1，l 2与x=a 交点距离，一次函数64=-+y kx k 的图象与线段AB （含端点）有公共点范围问题，掌握待定系数法求直线解析式，三角形面积求法，会求两直线l 1，l 2与x=a 交点距离，一次函数64=-+y kx k 的图象与线段AB （含端点）有公共点范围方法是解题关键．22．（1）见解析；（2）92． 【分析】（1）根据∠B=90°，PE ⊥AP ，即可得到∠BAP=∠CPE ，再根据∠B=∠C=90°，即可得出PEC APB ∽△△；（2）根据PEC APB ∽△△，得出EC=32，最后根据DE=CD-CE 求解即可． 【详解】解：（1）∵正方形ABCD 中，∠B=90°，PE ⊥AP ，∴∠BAP+∠APB=90°，∠CPE+∠APB=90°，∴∠BAP=∠CPE ，又∵∠B=∠C=90°，∴PEC APB ∽△△；（2）由（1）可得：PEC APB ∽△△，∵点P 为BC 的中点，∴BP=CP=3，∵AB=6，∵PEC APB ∽△△， ∴BP EC AB PC=，即363EC =， ∴EC=32， ∴DE=CD-CE=6-32=92．【点睛】本题考查正方形的性质，全等三角形的判定与性质，相似三角形的判定，解题的关键是掌握相关性质．23．（1）见详解；（2）2【分析】（1）利用相似三角形的判定定理，即可得到结论；（2）先证明AD ∥BE ，利用平行线分线段成比例，列出比例式，即可求解．【详解】（1）证明：∵D DCE ∠=∠，∠AFD=∠EFC ，∴ADF ECF ∽△△；（2）解：∵四边形ABCD 是平行四边形，∴AD ∥BE ，AB ＝CD ＝6，∴AF ：EF ＝DF ：CF ，又∵EF ＝2AF ，∴DF ：CF ＝1：2，即DF ＝13DC ＝2． 【点睛】本题考查的是平行四边形的性质及相似三角形的判定，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边、对顶角等隐含条件，以充分发挥基本图形的作用． 24．（1）见解析；（2）①BE=203；②81． 【分析】（1）由平行线的性质得出∠DEB=∠FCE ，∠DBE=∠FEC ，即可得出结论；（2）①由平行线的性质得出12BE AF EC FC ==，即可得出结果； ②先求出2,3FC AC =易证△EFC ∽△BAC ，由相似三角形的面积比等于相似比的平方即可得出结果．【详解】解：（1）证明：∵DE ∥AC ，∴∠DEB=∠FCE ，∵EF ∥AB ，∴∠DBE=∠FEC ，∴△BDE ∽△EFC ；（2）解：①∵EF ∥AB ， ∴12BE AF EC FC ==， ∵EC=BC-BE=20-BE ，∴1202BE BE =-， 解得：BE=203； ②∵12AF FC =， ∴2,3FC AC = ∵EF ∥AB ，∴△EFC ∽△BAC ， ∴2224()()39EFC ABC S FC S AC ∆∆===， ∴99368144ABC EFC S S ∆∆==⨯=． 【点睛】本题考查了相似三角形的判定与性质、平行线的性质等知识；熟练掌握相似三角形的判定与性质是解题的关键．25．（1）228833y x x =-++；（2）菱形，见解析；（3）P 755,26⎛⎫ ⎪⎝⎭ 【分析】（1）利用待定系数法求二次函数解析式；（2）利用对称的性质得∠E′CP=∠ECP ，E′C=CE ，E′P=EP ，由PE ∥E′C 得∠EPC=∠E′CP ，则∠EPC=∠ECP ，于是可判断EP=EC ，所以EC=EP=PE′=E′C ，则根据菱形的判定方法得到四边形EPE′C 为菱形；（3）先利用待定系数法求出直线BC 的解析式为228833y x x =-++，根据二次函数和一次函数图象上点的坐标特征，设P （x ，228833x x -++），则E （x ，-43x+8），则可计算出PE=228833x x -++-（-43x+8）=-23x 2+4x ，过点E 作EF ⊥y 轴于点F ，如图，证明△CFE ∽△COB ，利用相似比可计算出CE=53x ，则可利用EC=EP 得到方程-23x 2+4x=53x ，然后解方程求出x 即可得到P 点坐标．【详解】解：（1）把点C （0，8），B （6，0）代入在抛物线y=-23x 2+bx+c 得 2826603c b c =⎧⎪⎨-⨯++=⎪⎩，解得8 3 8bc⎧=⎪⎨⎪=⎩，∴抛物线的表达式为228833y x x=-++；（2）以P，C，E，E'为顶点的四边形为菱形．理由如下：∵E点和E'点关于直线PC对称，∴E CP ECP'∠=∠，E C CE'=，E P E'=，又∵PD x⊥轴，∴//PE E C'，∴EPC E CP'∠=∠，∴EPC ECP∠=∠，∴EP EC=，∴EC EP PE E C''===，∴四边形EPE C'为菱形，（3）设直线BC的解析式为y=kx+m，把B（6，0），C（0，8）代入得608k mm+=⎧⎨=⎩，解得438km⎧=-⎪⎨⎪=⎩，∴直线BC的解析式为y=-43x+8；设P（x，228833x x-++），则E（x，-43x+8），∴PE=228833x x-++-（-43x+8）=-23x2+4x，过点E 作EF ⊥y 轴于点F ，如图，在Rt △OBC 中，BC=22OB OC +=10， ∵EF ∥OB ，∴△CFE ∽△COB ，∴EF CE OB CB =，即610x CE =， ∴CE=53x ， ∵EC=EP ， ∴-23x 2+4x=53x ， 整理得2x 2-7x=0，解得x 1=0（舍去），x 2=72， ∴点P 的坐标为（72，556）． P 点坐标为755,26⎛⎫ ⎪⎝⎭． 【点睛】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、对称的性质和菱形的判定方法；会利用待定系数法求函数解析式；理解坐标与图形性质；会利用相似比计算线段的长和解一元二次方程．26．（1）画图见解析；1(2,1)C -；（2）画图见解析；2(4,2)C -．【分析】（1）根据题意得到A ，B ，C 关于原点O 的对称点连接即可；（2）根据位似图形的作图方法作图即可；【详解】解：（1）根据题意可得()11,3A -，()12,3B ，()12,1C -，如图，1(2,1)C -， （2）根据题意可得，()22,6A -，()24,6B ，()24,2C -连接即可，如图，2(4,2)C -．【点睛】本题主要考查了旋转变换和位似变换，准确作图是解题的关键．。

一、选择题1．在ABC 中，10AB AC ==，72ABC ∠=︒，ABC ∠的角平分线交AC 于点D ，则CD 的长为（ ）A ．5B ．555-C ．1555-D ．551-2．下列各组长度的线段（单位：cm ）中，成比例线段的是（ ）A ．2，3，4，5B ．1，3，4，10C ．2，3，4，6D ．1，5，3，123．如图，A B C '''是ABC 以点О为位似中心经过位似变换得到的，若:1:2OA A A ''=，则A B C '''的周长与ABC 的周长比是（ ）A ．1：2B ．1：3C ．1：4D ．4：94．如图，已知,//,//ABC DF BC DE AC △，四边形DECF 的面积为12,若DE 经过ABC 的重心，则ABC 的面积为（ ）A ．25B ．26C ．27D ．285．如图，在Rt ABC 中，90C ∠=︒，3AC =，4BC =，点D 是AB 的中点，点P 是直线BC 上一点，将BDP △沿DP 所在的直线翻折后，点B 落在1B 处，若1B D BC ⊥，则点P 与点B 之间的距离为（ ）A ．1或5B ．1或3C ．54或3 D ．54或56．已知等腰△ABC 的底角为75°，则下列三角形一定与△ABC 相似的是（ ） A ．顶角为30°的等腰三角形 B ．顶角为40°的等腰三角形 C ．等边三角形D ．顶角为75°的等腰三角形7．如图，在正方形ABCD 中，BPC △是等边三角形，BP 、CP 的延长线分别交AD 于点E 、F ，连接BD 、DP ，BD 与CF 相交于点H ，给出下列结论：①2BE AE =；②DFP BPH ∽△△；③PFD PDB ∽△△；④2DP PH PC =⋅．其中正确的是（ ）A ．①②③B ．①③④C ．②③④D ．①②④8．两个相似三角形面积比是4:9，其中一个三角形的周长为18，则另一个三角形的周长是（ ） A ．12B ．12或24C ．27D ．12或279．若ad=bc ，则下列不成立的是( ) A ．a cb d= B ．a c ab d b-=- C ．a b c db d++= D ．1 111a cb d ++=++ 10．如图，四个全等的直角三角形拼成“赵爽弦图”得到正方形ABCD 与正方形EFGH ．连结EG ，BD 相交于点O ，BD 与HC 相交于点P ．若GO GP =，下列结论：①GOP BCP ∠=∠，②BC BP =，③:21BG PG =+，④DP PO =．正确的是（ ）A ．②③④B ．①③④C ．①②④D ．①②③11．若ABC 的每条边长增加各自的20%得A B C '''，则B '∠的度数与其对应角B 的度数相比（ ） A ．增加了20%B ．减少了20%C ．增加了()120%+D ．没有改变12．如图，在△ABC 中，∠C ＝90°，AB ＝10，BC ＝8．E 是AC 边上一动点，过点E 作EF ∥AB 交BC 于点F ，D 为线段EF 的中点，当BD 平分∠ABC 时，AE 的长度是（ ）A ．1613B ．3013C ．4013D ．4813二、填空题13．已知高为2m 的标杆在水平地面上的影子长1.5m ，此时测得附近旗杆的影子长7.5m ．则旗杆的高为__m ．14．已知35a b =，则aa b+的值为______．15．在平面直角坐标中，△ABC 的顶点坐标分别是A （1，1），B （4，2），C （3，5），以点A 为位似中心，相似比为1：2，把三角形ABC 缩小，得到△AB 1C 1，则点C 的对应点C 1的坐标为_________．16．已知线段AB 长是2,P 是线段AB 上的一点，且满足2·,AP AB BP =那么AP 长为____．17．如图，四边形ABCD 与四边形EFGH 位似，位似中心点是O ，32OE EA =，则FGBC=________．18．如图，矩形ABCD 中，4=AD ，10AB =，P 为CD 边上的动点，当DP =_________时，ADP △与BCP 相似．19．如图，在Rt ABC △中，90C ∠=︒，棱长为1的立方体的表面展开图有两条边分别在AC ，BC 上，有两个顶点在斜边AB 上则图中阴影部分的面积为__________．20．如图，若ABC 与DEF 都是正方形网格中的格点三角形（顶点在格点上），则DEF 与ABC 的周长比为_________．三、解答题21．如图，已知直线CD 过点C(-2，0)和D(0，1)，且与直线AB ：y=-x+4交于点A ． （1）求直线CD 的解析式； （2）求交点A 的坐标；（3）在y 轴上是否存在一点P ，使得PBCABCS S？若存在，请直接写出P 点的坐标；若不存在，请说明理由．22．如图1，E ，F 分别是正方形ABCD 的边AD 和对角线AC 的中点， （1）CFDE的值为 ； （2）①将△AEF 绕点A 旋转，（1）中的结论是否仍然成立？如果成立，请仅就图2的情况进行证明；如果不成立，请说明理由；②如果AB ＝2，当以点E ，F ，C 在一条直线上时，请直接写出CF 的值．23．如图，a ∥b ∥c ，直线m ，n 与直线a ，b ，c 分别相交于点A ，B ，C 和点D ，E ，F ．若AB ＝3，BC ＝5，DE ＝4，求EF 的长．24．如图，ABC 的顶点坐标分别为()1,3A 、()4,2B 、()2,1C ． （1）以原点O 为位似中心，在原点另一侧画出111A B C △，使1112AB A B = （2）写出1A 的坐标______． （3）111A B C △的面积是______．25．如图，在正方形ABCD 中，E 为边AD 上的点，点F 在边CD 上，90BEF ︒∠=且3CF FD =．（1）求证：ABE DEF ∆∆；（2）若4AB =，延长EF 交BC 的延长线于点G ，求CG 的长．26．在如图的方格纸中，OAB 的顶点坐标分别为(00)(21)(13)----,,,,,O A B ，111O A B △与OAB 是关于点P 为位似中心的位似图形．（1）在图中标出位似中心P 的位置，并写出点P 及点B 的对应点1B 的坐标；（2）以原点O 为位似中心，在位似中心的同侧画出OAB 的一个位似22OA B △，使它与OAB 的位似比为2∶1，并写出点B 的对应点2B 的坐标．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】证明△ABC ∽△BCD ，得到AB BCBC CD=，设CD=x ，表示出BC ，代入得到方程，解之即可． 【详解】解：如图，∵AB=AC ，∠ABC=72°， ∴∠C=72°，∴∠A=180°-2×72°=36°， ∵BD 平分∠ABC ， ∴∠ABD=∠CBD=36°， ∴AD=BD ，∠BDC=72°， ∴BC=BD ，在△ABC 和△BCD 中， ∠A=∠CBD ，∠ABC=∠C ， ∴△ABC ∽△BCD ， ∴AB BCBC CD=， 设CD=x ，则BD=AD=BC=10-x ， ∴101010xx x-=-，解得：x=1555+（舍）或1555-， 故选C ．【点睛】本题考查了等腰三角形的判定和性质，相似三角形的判定和性质，解题的关键是根据已知条件证明出△ABC ∽△BCD ．2．C解析：C 【分析】判定四条线段是否成比例，计算前两条线段之比与后两条线段之比是否相等即可． 【详解】解：A.2:3≠4:5，故四条线段不成比例，不合题意； B.1:3≠4:10，故四条线段不成比例，不符合题意； C.2:3=4:6，故四条线段成比例，符合题意； D.1:5≠3:12，故四条线段不成比例，不合题意； 故选：C ． 【点睛】本题主要考查了成比例线段的定义，熟记概念并准确计算是解题的关键．3．B解析：B 【分析】根据位似变换的概念得到，A B ''∥AB ，A B C ABC '''∽△△，根据相似三角形的性质解答即可． 【详解】解：∵:1:2OA A A ''=， ∴13OA OA ':=:，∵A B C '''是ABC 以点O 为位似中心经过位似变换得到的， ∴A B ''∥AB ，A B C ABC '''∽△△， ∴13A B OA AB OA '''==， ∴A B C '''的周长与ABC 的周长比为1：3， 故选：B ． 【点睛】本题考查的是位似变换的概念和性质、相似三角形的性质，掌握位似的两个图形必须是相似形、对应边平行是解题的关键．4．C解析：C 【分析】 设重心为G ，则2BGGH=，根据三角形相似的判定与性质可得49BDE ABCS S =，19ADF ABCSS=，列出方程组并求解即可． 【详解】解：∵DE 经过ABC 的重心，设重心为G ，则2BGGH=，∵//,//DF BC DE AC ，∴△BDE ∽△BAC ，△ADF ∽△ABC ， ∴23DE BG BD AC BH AB ===， ∴13AD AB =， ∴49BDE ABCS S=，19ADF ABCS S=， ∴45BDEADFDECFS SS =+，18ADFBDEDECFSSS =+， ∴41251128BDEADF ADF BED S SS S ⎧=⎪+⎪⎨⎪=⎪+⎩，解得12BDES=，3ADFS=，∴27△ABC S =， 故选：C ． 【点睛】本题考查重心的性质、相似三角形的判定与性质，得到面积的比例关系是解题的关键．5．D解析：D【分析】分点B 1在BC 左侧，点B 1在BC 右侧两种情况讨论，由勾股定理可AB=5，由平行线可证△BED ∽△BCA ，可得12BD BE DE AB BC AC ===，可求BE ，DE 的长，由勾股定理可求PB 的长． 【详解】解：如图，若点B 1在BC 左侧，B 1D 交BC 于E ，∵∠C=90°，AC=3，BC=4， ∴225AC BC +， ∵点D 是AB 的中点， ∴BD=12BA=52， ∵B 1D ⊥BC ，∠C=90°， ∴B 1D ∥AC ，∴∠BDE=∠A ，∠EBD=∠CBA ， ∴△BED ∽△BCA ， ∴12BD BE DE AB BC AC ===， ∴BE=EC=12BC=2，DE=12AC=32， ∵折叠，∴B 1D=BD=52，B 1P=BP ， ∴B 1E=B 1D-DE=1，∴在Rt △B 1PE 中，B 1P 2=B 1E 2+PE 2， ∴BP 2=1+（2-BP ）2， ∴BP=54， 如图，若点B 1在BC 右侧，延长B 1D 交BC 与E ，∵B 1D ⊥BC ，∠C=90°， ∴B 1D ∥AC ，∴∠BDE=∠A ，∠EBD=∠CBA ， ∴△BED ∽△BCA ， ∴12BD BE DE AB BC AC ===， ∴BE=EC=12BC=2，DE=12AC=32， ∵折叠，∴B 1D=BD=52，B 1P=BP ， ∵B 1E=DE+B 1D=32+52， ∴B 1E=4，在Rt △EB 1P 中，B 1P 2=B 1E 2+EP 2， ∴BP 2=16+（BP-2）2， ∴BP=5，则点P 与点B 之间的距离为54或5． 故选择：D ． 【点睛】本题考查了折叠的性质、直角三角形的性质以及勾股定理，相似三角形判定与性质．此题难度适中，注意数形结合思想的应用，注意折叠中的对应关系．6．A解析：A 【分析】根据等腰三角形的性质得出等腰三角形的角的度数，进而利用相似三角形的判定解答即可． 【详解】解：∵等腰△ABC 的底角为75°，∴等腰△ABC 的三角的度数分别为30°，75°，75° ∴一定与△ABC 相似的是顶角为30°的等腰三角形 故选：A ． 【点睛】本题考查了想做浅咖人判定，关键是根据等腰三角形的性质得出等腰三角形的角的度数解答．7．D解析：D 【分析】由正方形ABCD ，与BPC △是等边三角形的性质求解，求解30,EBA ∠=︒ 从而可判断①；证明60,PFE BPC ∠=∠=︒ =15,PBH PDF ∠=∠︒ 可判断②；由15,30,15,60,PBD BDP PDF PFD ∠=︒∠=︒∠=︒∠=︒ 可判断③； 证明30,PDH PCD ∠=︒=∠ 再证明,PDH PCD ∽ 可得,DP PHPC PD=从而可判断 ④． 【详解】 解：正方形ABCD ，90,,ABC A BCD ADC CB CD AB ∴∠=∠=∠=∠=︒==BPC △是等边三角形，60,PBC PCB BPC ∴∠=︒=∠=∠ 906030,EBA ∴∠=︒-︒=︒2,BE AE ∴= 故①符合题意；正方形ABCD ，//,45,AD BC CBD ∴∠=︒ 60,PFE PCB ∴∠=∠=︒ 60,PFE BPC ∴∠=∠=︒BPC △是等边三角形，,PC BC CD ∴==而906030,PCD ∠=︒-︒=︒()11803075,2CDP ∴∠=︒-︒=︒ 907515,PDF ∴∠=︒-︒=︒由60,45,PBC CBD ∠=︒∠=︒15,PBH ∴∠=︒ ,PBH PDF ∴∠=∠,BPH DFP ∴∽ 故②符合题意；15,30,15,60,PBD BDP PDF PFD ∠=︒∠=︒∠=︒∠=︒ ,PFD BPD ∴不相似，故③不符合题意；正方形ABCD ，45CDB ∴∠=︒，90451530,PDH PCD ∴∠=︒-︒-︒=︒=∠,DPH CPD ∠=∠ ,PDH PCD ∴∽ ,DP PHPC PD∴= ∴ 2DP PH PC =⋅，故④符合题意，综上：符合题意的有：①②④． 故选：.D 【点睛】本题考查的是等边三角形的性质，含30的直角三角形的性质，正方形的性质，相似三角形的判定与性质，掌握以上知识是解题的关键．8．D解析：D 【分析】把面积之比转化为周长之比，后分周长为较大三角形或较小三角形的两种情形求解即可. 【详解】∵两个相似三角形面积比是4:9， ∴两个相似三角形周长比是2：3， 当较大三角形的周长为18时，较小三角形的周长为18×23=12； 当较小三角形的周长为18时，较大三角形的周长为18×32=27； 故选D. 【点睛】本题考查了相似三角形面积之比，周长之比，解答时，熟练将面积之比转化为周长之比，会用分类思想求解是解题的关键.9．D解析：D 【分析】根据比例和分式的基本性质，进行各种演变即可得到结论． 【详解】 A 由a cb d=可以得到ad=bc ，故本选项正确，不符合题意； B 、由a c ab d b-=-可得：（a-c ）b=（b-d ）a ，即ad=bc ，故本选项正确，不符合题意； C 、由a b c db d++=可得（a+b ）d=（c+d ）b ，即ad=bc ，故本选项正确，不符合题意；D 、由1?111a cb d ++=++，可得（a+1）（d+1）=（b+1）（c+1），即ad+a+d=bc+c ，不能得到ad=bc ，故本选项错误，符合题意； 故选：D ． 【点睛】本题考查了比例线段，根据比例的性质能够灵活对一个比例式进行变形．10．D解析：D 【分析】由正方形的性质证明180BOG BCG ∠+∠=︒，结合180BOG GOP ∠+∠=︒， 从而可判断①；由GO GP =，可得,GOP GPO ∠=∠从而可得,GPO BCP ∠=∠可判断②；设,,BG a CG b == 则,DH CG BF b === 再证明,DHP BGP ∽ 可得,DH HPBG PG= 求解2,b HP a= 再证明,PG b = 利用,HG HP PG =+ 列方程2,b a b b a -=+解关于a 的方程并检验即可判断③；证明,DHP CHD ∽求解DP =再证明,BCP GPO ∽ 求解PO = 由,a b ≠ 可判断④，从而可得答案．【详解】解：正方形ABCD 与正方形EFGH ．45,45,DBC EGF ∴∠=︒∠=︒ 90,BGC ∠=︒4590135,EGC ∴∠=︒+︒=︒36036045135180,BOG BCP OBC OGC ∴∠+∠=︒-∠-∠=︒-︒-︒=︒ 180,BOG GOP ∠+∠=︒∴ GOP BCP ∠=∠，故①符合题意；GO GP =，,GOP GPO ∴∠=∠ ,GPO BCP ∴∠=∠ ,BC BP ∴= 故②符合题意；正方形,FGHE//,EH FG ∴ ,DHP BGP ∴∽,DH HPBG PG∴= 设,,BG a CG b == 则,DH CG BF b ===,,BC BP BG PC =⊥ ,PG CG b ∴==,b HP a b∴= 2,b HP a∴=,FG HG HP PG a b ==+=-2,b a b b a∴-=+2220,a ba b ∴--=(21,2b a b ±∴==±经检验：(1a b =-不合题意，舍去，(1,a b ∴=+(11b BG a PG b b∴===+故③符合题意；,,BC BP BG CP =⊥,CBG PBG ∴∠=∠ //,DE BG ,HDP PBG ∴∠=∠ ,CBG DCH ∠=∠ ,HDP DCH ∴∠=∠ ,DHP CHD ∠=∠ ,DHP CHD ∴∽,DH DPCH CD∴= ,,DH b CH BG a ===CD ∴=b a∴=DP ∴=45,,,CBP PGO BC BP GP GO ∠=︒=∠==,BC BPPG GO∴= ,BCP GPO ∴∽ ,BC CPGP PO∴=22,BC CD PC CG b ====2,b PO =PO ∴=,a b ≠,DP PO ∴≠ 故④不符合题意；故选：.D 【点睛】本题考查的是四边形的内角和定理，等腰三角形的判定与性质，勾股定理的应用，正方形的性质，二次根式的运算，一元二次方程的解法，三角形相似的判定与性质，掌握以上知识是解题的关键．11．D解析：D 【分析】根据两个三角形三边对应成比例，这两个三角形相似判断出两个三角形相似，再根据相似三角形对应角相等解答． 【详解】解：∵△ABC 的每条边长增加各自的20%得△A′B′C′， ∴△ABC 与△A′B′C′的三边对应成比例， ∴△ABC ∽△A′B′C′， ∴∠B′=∠B ． 故选：D ． 【点睛】本题考查了相似图形，熟练掌握相似三角形的判定是解题的关键．12．B解析：B 【分析】根据角平分线、中点及平行线的性质，得出FD=ED= FB ，设FD=ED= FB=x ，再根据△CEF ∽△CAB ，得出x 的值，根据勾股定理即可求解． 【详解】解：∵BD 平分∠ABC ∴∠ABD=∠FBD∵EF ∥AB ∠FDB=∠ABD ∴∠FDB=∠FBD ∴△FBD 为等腰三角形 ∴FB=FD∵D 为线段EF 的中点 ∴FD=ED ∴FD=ED= FB 设FD=ED= FB=x ∴EF=2x ∵EF ∥AB ∴△CEF ∽△CAB∴CF EFCB AB= ∴CB FB EFCB AB -= 即8-2810x x= 解得：x=4013∴CF=8-BF=8-4013=6413 EF=2×4013=8013∵∠C ＝90°，AB ＝10，BC ＝8∴=在Rt △CEF 中=4813∴AE=AC-CE=6-4813=3013故选：B ． 【点睛】本题主要考查了角平分线、中点及平行线的性质，也考察了相似三角形的性质，勾股定理的应用；解题关键是熟练掌握角平分线、平行线以及相似三角形的性质以及利用方程解决实际问题．第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题13．【分析】根据题意标杆光线影长组成的三角形与旗杆旗杆影长光线所组成的三角形相似故可利用相似三角形的性质解答【详解】解：设旗杆的高度为x 米根据题意得：解得：x ＝10故答案为：10【点睛】本题考查了相似三 解析：10【分析】根据题意，标杆、光线、影长组成的三角形与旗杆、旗杆影长、光线所组成的三角形相似，故可利用相似三角形的性质解答． 【详解】解：设旗杆的高度为x 米，根据题意得：21.57.5x =， 解得：x ＝10． 故答案为：10． 【点睛】本题考查了相似三角形的应用，只要是把实际问题抽象到相似三角形中，利用相似三角形的相似比，列出方程，通解方程求出树的高度，体现了方程的思想．14．【分析】根据比例的性质求解即可；【详解】∵设∴；故答案是【点睛】本题主要考查了比例的性质准确计算是解题的关键 解析：38【分析】根据比例的性质求解即可； 【详解】∵35a b =， 设3a k =，5b k =，∴33358a k ab k k ==++； 故答案是38．【点睛】本题主要考查了比例的性质，准确计算是解题的关键．15．(23)或(0-1)【分析】以A 点为坐标原点建立新的直角坐标系得知C 点在新的直角坐标系中的坐标再根据相似比可求出C1在新的直角坐标系中的坐标最后即可知道点C1在原坐标系中的坐标【详解】以A 点为坐标原解析：(2，3)或(0，-1) 【分析】以A 点为坐标原点建立新的直角坐标系，得知C 点在新的直角坐标系中的坐标，再根据相似比，可求出C 1在新的直角坐标系中的坐标，最后即可知道点C 1在原坐标系中的坐标． 【详解】以A 点为坐标原点建立新的直角坐标系，则在新的直角坐标系中，C 点的坐标为(3-1，5-1)，即C(2，4)．根据题意可知在新的直角坐标系中11AB C △是以点A 为位似中心，相似比为1：2，把ABC 缩小后得到的三角形．∵点C 在新的直角坐标系中的坐标为(2，4)，∴点C 的对应点C 1在新的直角坐标系中的坐标为()112422⨯⨯，或()112422⨯-⨯-，，即(1，2)或(-1，-2)．∴点C 1在原坐标系中的坐标为(1+1，2+1)或(-1+1，-2+1)，即(2，3)或(0，-1)． 故答案为(2，3)或(0，-1)． 【点睛】本题考查的是位似图形，熟练掌握位似变换是解题的关键．16．【分析】先证出点P 是线段AB 的黄金分割点再由黄金分割点的定义得到把AB=2代入计算即可【详解】解：∵点P 在线段AB 上AP2=AB•BP ∴点P 是线段AB 的黄金分割点AP ＞BP 故答案为：【点睛】本题考查1【分析】先证出点P 是线段AB 的黄金分割点，再由黄金分割点的定义得到12AP AB =，把AB=2代入计算即可． 【详解】解：∵点P 在线段AB 上，AP 2=AB•BP ， ∴点P 是线段AB 的黄金分割点，AP ＞BP ，21AB AP ===∴，1． 【点睛】本题考查了黄金分割的概念：如果一个点把一条线段分成两条线段，并且较长线段是较短线段和整个线段的比例中项，那么就说这个点把这条线段黄金分割，这个点叫这条线段的黄金分割点，较长线段是整个线段的12倍． 17．【分析】由得即得到位似比根据位似的性质计算即可【详解】∵∴即∵四边形与四边形位似∴故答案为【点睛】本题考查了图形的位似准确将线段的比转化为位似图形的位似比是解题的关键解析：35. 【分析】由32OE EA =，得323OE EA OE =++即35OE OA =，得到位似比，根据位似的性质计算即可. 【详解】∵32OE EA =，∴323OE EA OE =++，即35OE OA =， ∵四边形ABCD 与四边形EFGH 位似，∴FG BC =35OE OA =， 故答案为35. 【点睛】本题考查了图形的位似，准确将线段的比转化为位似图形的位似比是解题的关键.18．2或8或5【分析】需要分类讨论：△ADP ∽△BCP 和△ADP ∽△PCB 根据该相似三角形的对应边成比例求得DP 的长度【详解】∵四边形ABCD 是矩形AD ＝4AB ＝10∴BC ＝AD ＝4CD ＝AB ＝10设D解析：2或8或5 【分析】需要分类讨论：△ADP ∽△BCP 和△ADP ∽△PCB ，根据该相似三角形的对应边成比例求得DP 的长度． 【详解】∵四边形ABCD 是矩形，AD ＝4，AB ＝10 ∴BC ＝AD ＝4，CD ＝AB ＝10，设DP ＝x ，则CP ＝10－x ， 分两种情况进行讨论： ①当△ADP ∽△BCP 时，AD DPBC CP =，即4410x x=- ∴()4104x x ⨯-=， 解得：5x =； ②当△ADP ∽△PCB 时， AD DP PC BC=，即4104xx =-， ∴()1016x x -= 解得：x=2或x=8， 故答案为：2或8或5． 【点睛】本题主要考查的就是三角形相似的问题和动点问题，首先将各线段用含x 的代数式进行表示，然后看是否有相同的角，根据对应角的两边对应成比例将线段写成比例式的形式，然后分别进行计算得出答案．在解答这种问题的时候千万不能出现漏解的现象，每种情况都要考虑到位．19．10【分析】由题意得是直角三角形四边形DEGC 是矩形易证再根据ASA 证明然后根据相似三角形的性质和全等三角形的性质得出从而求出AG 的值根据即可求出三角形ABC 的面积再减去6个边长为1的小正方形的面积解析：10 【分析】 由题意得BDE 、EHF 、EGA △是直角三角形，四边形DEGC 是矩形，//,////,231BC EG DE HF AC DE HF DC EG HE =====，，,易证EHF EGA △△，再根据ASA 证明BDE EHF ≅△△，然后根据相似三角形的性质和全等三角形的性质得出123AG=，从而求出AG 的值，根据 ABC BDE EGA DEGC S S S S =++△△△矩形即可求出三角形ABC 的面积，再减去6个边长为1的小正方形的面积即为阴影部分的面积． 【详解】 解：如图：由题意得：BDE 、EHF 、EGA △是直角三角形，四边形DEGC 是矩形，//,////,231BC EG DE HF AC DE HF DC EG HE =====，，,90BDE EHF EGA ∴∠=∠=∠=︒∠∠∠，DEB=HFE=GAEEHFEGA ∴△△ HE HF EG AG∴= 在BDE 和EHF 中BDE EHF DE HFDEB HFE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()BDE EHF ASA ∴≅△△，1DB HE ∴==，123AG∴=， 6AG ∴=，11=123623=1622ABC BDE EGA DEGC S S S S ∴=++⨯⨯+⨯⨯+⨯△△△矩形， ∴S 阴影=S △ABC -6=16-6=10，故答案为：10．【点睛】本题考查了相似三角形的判定及性质、全等三角形的判定及性质，熟练掌握性质定理是解题的关键．20．【分析】设正方形网格的边长为1根据勾股定理求出△EFD △ABC 的边长运用三边对应成比例则两个三角形相似这一判定定理证明△EDF ∽△BAC 即可解决问题【详解】解：设正方形网格的边长为1由勾股定理得：D【分析】设正方形网格的边长为1，根据勾股定理求出△EFD 、△ABC 的边长，运用三边对应成比例，则两个三角形相似这一判定定理证明△EDF ∽△BAC ，即可解决问题．【详解】解：设正方形网格的边长为1，由勾股定理得：DE 2＝22+22，EF 2＝22+42，∴DE ＝EF ＝同理可求：AC，BC∵DF ＝2，AB ＝2，∴1EF DE DF BC AB AC === ∴△EDF ∽△BAC ，∴DEF 与ABC，．【点睛】本题主要考查了勾股定理和相似三角形的判定及其性质，熟练掌握相似三角形的判定与性质是解题的关键．三、解答题21．（1）y=12x+1；（2）(2，2)；（3）存在，(0，2)或(0，-2) 【分析】（1）直线CD 过点C(-2，0)和D(0，1)，设直线CD 解析式为y kx b =+，将C(-2，0)和D(0，1)代入得-2=01k b b +⎧⎨=⎩解方程组即可； （2）联立方程1124y x y x ⎧=+⎪⎨⎪=-+⎩，解方程组即可； （3）△PBC 与△ABC 的底均为BC ，当面积相等时，则高也相等，由△ABC 的底BC 边上的高为A 点的纵坐标2，可求P 点的纵坐标的绝对值为2，点P 在y 轴上，分类考虑点P 的位置即可求出．【详解】解：（1）直线CD 过点C(-2，0)和D(0，1)，设直线CD 解析式为y kx b =+，将C(-2，0)和D(0，1)代入得，-2=01k b b +⎧⎨=⎩， 解得1=21k b ⎧⎪⎨⎪=⎩，直线CD 的解析式为y=12x+1； （2）联立方程1124y x y x ⎧=+⎪⎨⎪=-+⎩，解得22x y =⎧⎨=⎩， A 点坐标为（2，2）；（3）△PBC 与△ABC 的底均为BC ，当面积相等时，则高也相等，∵△ABC 的底BC 边上的高为A 点的纵坐标2，∴P 点的纵坐标的绝对值为2，点P 在y 轴上，①当点P 在x 轴上方时，则P 点坐标为（0，2）；②当点P 在x 轴下方时，则P 点坐标为（0，-2）；综上所述，点P 的坐标为（0，2）或（0，-2）．【点睛】本题考查待定系数法求直线解析式，两直线交点坐标，同底等高三角形面积问题，掌握待定系数法求直线解析式，两直线交点坐标联立两直线方程解方程组，同底等高三角形面积分类处理是解题关键．22．（12；（2）①仍然成立，理由见解析；7．【分析】（1）由四边形ABCD 是正方形可知2AC ＝．又因为E ，F 分别是正方形ABCD 的边AD 和对角线AC 的中点，即可推出2=22CF DE ，即=2CF DE． （2）①因为△AFE 和△ACD 都是等腰直角三角形，可推出△AFE ∽△ACD ，即得出结论，=2AF AC AE AD=∠FAE ＝∠CAD ＝45°，可推出∠FAC ＝∠EAD ，即证明△ACF ∽△ADE ，即得出结论2CF AC DE AD= ②由题意可知AD ＝CD ＝AB ＝2， EF ＝AE ＝12AD ＝1，∠ADC ＝90°，∠AEF ＝90°．因为点E ，F ，C 在一条直线上，说明∠AEC ＝90°．在Rt AEC 中，利用勾股定理可求出CE 的长度，即可求出CF 的长度．【详解】解：（1）∵四边形ABCD 是正方形，∴AD ＝CD ，∠D ＝90°，∴2AC AD ＝， ∵E ，F 分别是正方形ABCD 的边AD 和对角线AC 的中点，∴=2=2AD DE AC CF ，，∴2=22CF DE ⨯，即=2CF DE． （2）①（1）中的结论仍然成立，理由如下：∵△AFE 和△ACD 都是等腰直角三角形，∴△AFE ∽△ACD ，∴=2AF AC AE AD=， ∵∠FAE ＝∠CAD ＝45°，∴∠FAE +∠CAE ＝∠CAD +∠CAE ，即∠FAC ＝∠EAD ，∴△ACF ∽△ADE ，∴=2CF AC DE AD=． ②如图3所示： ∵四边形ABCD 是正方形，∴AD ＝CD ＝AB ＝2，∠ADC ＝90°，∴222AC AD ==同②得：EF ＝AE ＝12AD ＝1，∠AEF ＝90°， ∵点E ，F ，C 在一条直线上，∴∠AEC ＝90°，在Rt AEC 中，22==81=7CE AC AE --，∴CF ＝CE +EF ＝71+．【点睛】本题为四边形综合题，掌握正方形的性质，相似三角形的判定和性质，等腰直角三角形的性质以及勾股定理是解答本题的关键．23．203【分析】根据平行线分线段成比例定理列出比例式，把已知数据代入计算即可．【详解】解：∵a ∥b ∥c ，AB ＝3，BC ＝5，DE ＝4，∴AB DE BC EF =，即345EF=， 解得，EF 203=， 故答案为：203． 【点睛】 本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键． 24．（1）见解析；（2）()12,6A --；（3）10【分析】 （1）根据位似图形的性质即可以原点O 为位似中心，在原点另一侧画出111A B C △，使1112AB A B =； （2）结合（1）即可写出A 1的坐标；（3）根据网格利用割补法即可求出111A B C △的面积．【详解】解：（1）如图，111A B C △为所求．（2）由图可知：()12,6A --．故答案为：()2,6--．（3）111A B C △的面积是：1114626242410222⨯-⨯⨯-⨯⨯-⨯⨯=． 故答案为：10．【点睛】本题考查了作图−位似变换，解决本题的关键是掌握位似图形的性质．25．（1）见解析；（2）6【分析】（1）先根据正方形的性质得到90A D ︒∠=∠=，AB BC CD AD ===，//AD BC ；然后再说明ABE DEF ∠=∠即可证明ABE DEF ∆∆；（2）先求得1DF =、3CF =，再根据相似三角形的性质得到AE AB DF DE =，进而求得DE=2,然后再根据EDFGCF ∆∆的性质求得CG 即可．【详解】解：（1）证明：四边形ABCD 为正方形， 90A D ︒∴∠=∠=，AB BC CD AD ===，//AD BC ，90BEF ︒∠=，90ABE AEB DEF AEB ︒∴∠+∠=∠+∠=，ABE DEF ∴∠=∠，ABE DEF ∴∆∆；（2）解：4AB BC CD AD ====，3CF DF =，1DF ∴=，3CF =，ABE DEF ∆∆，AE AB DF DE ∴=，即441DE DE-=，解得：2DE =， //AD BC ，EDF GCF ∆∆，DE DF CG CF ∴=，即213CG =， 6CG ∴=．【点睛】本题主要考查了正方形的性质、相似三角形的判定与性质，正确运用相似三角形的判定定理是解答本题的关键．26．（1）画图见解析，1(5,1),(3,5)---P B（2）画图见解析，226)(--，B 【分析】（1）连接1O O 并延长与1A A 的延长线相交，交点即为位似中心P ，再根据平面直角坐标系写出点P 和1B 的坐标；（2）延长OA 到2A ，使2=AA OA ，延长OB 到2B ，使2=BB OB ，连接22A B ，再根据平面直角坐标系写出点2B 的坐标；【详解】解：（1）位似中心P 如图所示，1(5,1),(3,5)---P B ；（2）22OA B △如图所示，226)(--，B ；【点睛】本题考查了利用位似变换作图，熟练掌握位似变换的性质准确找出对应点的位置是解题的关键．。

青岛版2020九年级数学1.4图形的位似自主学习基础过关练习题2（附答案详解） 1．如图所示，正方形EFGH 是由正方形ABCD 经过位似变换得到的，点O 是位似中心，E ，F ，G ，H 分别是OA ，OB ，OC ，OD 的中点，则正方形EFGH 与正方形ABCD 的面积比是（ ）A ．1：6B ．1：5C ．1：4D ．1：22．如图，DEF ∆是由ABC ∆经过位似变换得到的，O 点是位似中心，OD 2DA 3=，则DEF ∆与ABC ∆的面积比为（ ）A ．2：3B ．4：9C ．2：5D ．4：253．如图，在平面直角坐标系中，与ΔABC 是位似图形的是A ．①B ．②C ．③D ．④4．已知正△ABC 的中心为O ，边长为1．将其沿直线l 向右不滑动的翻滚一周时，其中心O 经过的路径长是（ ）A 433πB 233C ．4πD ．2π 5．在平面直角坐标系中，已知点A （﹣4，2），B （﹣6，﹣4），以原点O 为位似中心，相似比为12，把△ABO 缩小，则点A 的对应点A ′的坐标是（ ） A ．（﹣2，1） B ．（﹣8，4）C ．（﹣8，4）或（8，﹣4）D ．（﹣2，1）或（2，﹣1）6．在直角坐标系中，已知点(6 3)A -，，以原点O 为位似中心，相似比为13，把线段OA 缩小为'OA ，则点A '的坐标为（ ）A ．(21)-，，(21)--，B ．(21)-，，(21)，C ．(21)，，(21)--， D ．(21)-，，(21)-， 7．如图,已知BC ∥DE ，则下列说法不正确的是( )A ．两个三角形是位似图形B ．点A 是两个三角形的位似中心C ．AE ∶AD 是相似比 D ．点B 与点E ，点C 与点D 是对应位似点 8．如图，图中的每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点．若△ABC 与△A 1B 1C 1是位似图形，且顶点都在格点上，则位似中心的坐标是（ ）A ．(0,9)B ．(8,0)C ．(9,0)D ．(10,0)9．如图，点()8,6P 在ABC ∆的边AC 上，以原点O 为位似中心，在第一象限内将ABC ∆缩小到原来的12，得到'''A B C ∆，点P 在''A C 上的对应点P'的的坐标为( )A ．()4,3B ．()3,4C ．()5,3D ．()4,410．在平面直角坐标系中，将一个四边形各顶点的横、纵坐标都乘2，所得图形与原图形相比，下列说法正确的是( )A ．所得图形相当于将原图形横向拉长为原来的2倍，纵向不变B ．所得图形相当于将原图形纵向拉长为原来的2倍，横向不变C ．所得图形形状不变，面积扩大为原来的4倍D ．所得图形形状不变，面积扩大为原来的2倍11．在平面直角坐标系中，点C 、D 的坐标分别为C(3，-2)、D(1，0)，现以原点为位似中心，将线段CD 放大得到线段AB ，若点D 的对应点B 在x 轴上且OB=2则点C 的对应点A 的坐标为______.12．如图，△ABC 三个顶点的坐标分别为A(2，2)，B(4，2)，C(6，4)，以原点为位似中心，将△ABC 缩小，使变换得到的△DEF 与△ABC 对应边的比为1∶2，则线段AC 的中点P 变换后对应点的坐标为____．13．如图，线段两个点的坐标分别为，，以原点为位似中心，将线段缩小得到线段，若点的坐标为，则点的坐标为______．14．如图，在平面直角坐标系中，ABC 和A B C '''是以坐标原点O 为位似中心的位似图形，且'OB BB =, 如果点(23)A ，，那么点A '的坐标为_______．15．ABC ∆三个顶点坐标分别为()()()2,2,4,5,5,2A B C ---，以原点O 为位似中心，将这个三角形放大为原来的2倍. 相应坐标是_____ （写出一种即可）16．△ABC 与△DEF 是位似图形，且△ABC 与△DEF 的位似比是1：2，已知△ABC 的面积是2，则△DEF 的面积是____．17．在Rt △ABC 中，∠BAC =90，AB =AC ，AD ⊥BC 于点D ，P 是线段AD 上的一个动点，以点P 为直角的顶点，向上作等腰直角三角形PBE ，连接DE ，若在点P 的运动过程中，DE 的最小值为3，则AD 的长为____．18．如图，等腰三角形OBA和等腰三角形ACD的位似图形，则这两个等腰三角形位似中心的坐标是______．19．如图，以点C（0，1）为位似中心，将△ABC按相似比1：2缩小，得到△DEC，则点A（1，﹣1）的对应点D的坐标为____．20．如图1，矩形ABCD中，AB＝8，AD＝6；点E是对角线BD上一动点，连接CE，作EF⊥CE交AB边于点F，以CE和EF为邻边作矩形CEFG，作其对角线相交于点H．（1）如图2，当点F与点B重合时，求CE和CG的长；（2）如图3，当点E是BD中点时，求CE和CG的长；（3）在图1，连接BG，当矩形CEFG随着点E的运动而变化时，猜想△EBG的形状？并加以证明．21．正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫格点三角形．在图中正方形网格（每个小正方形边长为1）中有一格点△ABC和一线段DE （1）以DE为一边做格点△DEF与△ABC相似；（2）直接写出△DEF 的面积．22．如图，正方形ABCD ，点P 在射线CB 上运动(不包含点B 、C)，连接DP ，交AB 于点M ，作BE ⊥DP 于点E ，连接AE ，作∠FAD=∠EAB ，FA 交DP 于点F ．(1)如图a ，当点P 在CB 的延长线上时，①求证：DF=BE ；②请判断DE 、BE 、AE 之间的数量关系并证明；(2)如图b ，当点P 在线段BC 上时，DE 、BE 、AE 之间有怎样的数量关系？请直接写出答案，不必证明；(3)如果将已知中的正方形ABCD 换成矩形ABCD ，且AD ：AB=3：1，其他条件不变，当点P 在射线CB 上时，DE 、BE 、AE 之间又有怎样的数量关系？请直接写出答案，不必证明．23．如图，在方格运中（每个小方格的边长都是1个单位）有一点O 和ABC ∆.(1)画图：以点0为位似中心，把ABC ∆缩小为原来的一半（不改变方向），得到A B C '''∆；(2)ABC ∆与A B C '''∆的相似比为______.24．如图，已知△PAB 的三个顶点落在格点上．（注：每个小正方形的边长均为1）．（1）△PAB 的面积为 ；（2）在图①中，仅用直尺画出一个以A 为位似中心，与△PAB 相似比为1：2的三角形；（3）在图①中，画一个以AB 为边且面积为6的格点三角形ABC ，符合条件的点C 共 个；（4）在图②中，只借助无刻度的直尺，在图中画出一个以AB 为一边且面积为12的矩形ABMN ．25．如图，每个小方格都是边长为1个单位长度的小正方形，ABC ∆的三个顶点都在小正方形的格点上，按照下列要求作图：（1）将ABC ∆绕点O 顺时针旋转90︒，画出旋转后的的A B C '''∆；（2）以点O 为位似中心，作出ABC ∆的位似图形A B C ''''''∆，使它们分别位于点O 的两侧，且位似比1:2.26．如图，在矩形ABCD 中，AB ＝3，BC ＝4，动点P 从点D 出发沿DA 向终点A 运动，同时动点Q 从点A 出发沿对角线AC 向终点C 运动．过点P 作PE ∥DC ，交AC 于点E ，动点P 、Q 的运动速度是每秒1个单位长度，运动时间为x 秒，当点P 运动到点A 时，P 、Q 两点同时停止运动．设PE ＝y ；（1）求y 关于x 的函数关系式；（2）探究：当x 为何值时，四边形PQBE 为梯形？（3）是否存在这样的点P 和点Q ，使P 、Q 、E 为顶点的三角形是等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．27．在平面直角坐标系中，△ABC的三个顶点坐标分别为A(1，0)，B(0，−2)，C(2，−1)；（1）以原点O为位似中心，在第二象限画出△A1B1C1，使△A1B1C1与△ABC的位似比为2：1；（2）点P（a，b）为线段AC上的任意一点，则点P在△A1B1C1中的对应点P1的坐标为．参考答案1．C【解析】【分析】由正方形EFGH是由正方形ABCD经过位似变换得到的，点O是位似中心，E，F，G，H 分别是OA，OB，OC，OD的中点，易求得位似比等于EH：AD=1：2，又由相似三角形面积的比等于相似比的平方，即可求得正方形EFGH与正方形ABCD的面积比．【详解】∵正方形EFGH是由正方形ABCD经过位似变换得到的，点O是位似中心，∴正方形EFGH∽正方形ABCD，∵E，F，G，H分别是OA，OB，OC，OD的中点，∴EH=12 AD，即位似比为：EH：AD=1：2，∴正方形EFGH与正方形ABCD的面积比是：1：4．故选C．【点睛】此题考查位似变换，解题关键在于利用相似的性质进行解答.2．D【解析】【分析】根据位似变换的性质得到△DEF∽△ABC，根据题意求出相似比，根据相似三角形的性质解答即可．【详解】∵△DEF是由△ABC经过位似变换得到的，∴△DEF∽△ABC，∵OD2 DA3=，∴25ODOA=，即△DEF与△ABC的相似比为25，∴△DEF与△ABC的面积比是4：25，故选D．【点睛】本题考查的是位似变换的概念、相似三角形的性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．3．C【解析】【分析】直接利用位似图形的性质解答即可．【详解】因为图③与△ABC这两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，所以与△ABC是位似图形的是③．故选C．【点睛】本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．4．B【解析】【分析】先过C点作AB的垂线，求出旋转是弧的半径，旋转的角度，再根据旋转的次数即可得到结果.【详解】如图，过点C作CD⊥AB于D，则CD一定经过点O，∵CD＝32BC＝32．∴OC＝23CD＝33．根据等边三角形的性质，∠BCD＝12∠ACB＝12×60°＝30°，∴每一次翻滚中心O旋转的角度为：180°﹣2×30°＝120°，等边三角形翻滚3次翻滚一周，∴点O旋转的角度为：120°×3＝360°，∴中心O经过的路径长是：2π•OC＝故选：B【点睛】此题重点考察学生对图形旋转的理解，把握旋转前后的图形性质是解题的关键.5．D【解析】【分析】根据在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k，即可求得答案．【详解】∵点A（-4，2），B（-6，-4），以原点O为位似中心，相似比为12，把△ABO缩小，∴点A的对应点A′的坐标是：（-2，1）或（2，-1）．故选D．【点睛】此题考查了位似图形与坐标的关系．此题比较简单，注意在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标比等于±k．6．D【解析】【分析】根据相似比将线段OA缩小，又因为原点O为位似中心可得有两个符合的点，即可求出本题答案.【详解】∵相似比为13，当A点在第四象限时，所以可得A1’＝(6×13，－3×13)＝（2，－1）；根据位似的性质可知在第二象限亦有一点，因为第二象限的点和第四象限的点互为相反数，所以可得A2’（－2，1）.故答案为：D.【点睛】本题考查了位似的定义，熟练掌握该知识点是本题解题的关键.7．C【解析】【分析】直接利用位似图形的性质与定义分别进行分析可得答案.【详解】解：A.∵BC∥DE，且BE与CD相交于点A，∴两个三角形是位似图形，正确，不符合题意；B.点A是两个三角形的位似中心，正确，不符合题意；C. AE︰AB是相似比，故此选项错误，符合题意；D. 点B与点E，点C与点D分别是对应点，正确，不符合题意.故选C.【点睛】此题主要考查了位似变换，正确把握位似图形的定义与性质是解题的关键. 8．C【解析】【分析】利用位似图形的性质得出对应点的连线的交点即可得出答案．【详解】解：如图所示：点D即为所求，坐标为：（9，0）．故选：C．【点睛】本题考查位似变换，利用位似图形的性质得出位似中心的位置是解题关键．9．A【解析】【分析】根据位似的性质解答即可.【详解】解：∵点P（8，6）在△ABC的边AC上，以原点O为位似中心，在第一象限内将△ABC缩小到原来的12，得到△A′B′C′，∴点P在A′C′上的对应点P′的的坐标为：（4，3）．故选A．【点睛】此题主要考查了位似变换，正确得出位似比是解题关键．如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k，进而结合已知得出答案．10．C【解析】【分析】根据图形的相似判断出前后两个图形是相似图形,再利用相似图形面积比等于相似比的平方即可解题.【详解】解：由相似的性质可知, 将一个四边形各顶点的横、纵坐标都乘2，图形的形状不发生改变,并且这两个图形为相似图形,相似比为2:1,∴图形的面积比为4:1,∴图形的面积扩大4倍,故选C.【点睛】本题考查了图形的相似,相似图形坐标的特征,中等难度,熟悉相似图形的性质是解题关键. 11．（6，-4）或（-6,4）【解析】【分析】正确画出图形，利用位似图形的性质结合对应点坐标与位似比的关系得出C点坐标．注意有两解．【详解】解：如图，由题意，位似中心是O，位似比为2，∴OC=AC，∵C（3，-2），∴A（6，-4）或（-6，4），故答案为（6，-4）或（-6，-4）【点睛】本题考查位似变换、坐标与图形的性质等知识，学会正确画出图形解决问题，注意一题多解．解题的关键是正确把握位似比与对应点坐标的关系是解题关键．12．(2，32)或(－2，－32) 【解析】【分析】 位似变换中对应点的坐标的变化规律：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标的比等于k 或−k ．本题中k ＝2或−2．【详解】解：∵两个图形的位似比是1：（−12）或1：12，AC 的中点是（4，3）， ∴对应点是（2，32）或（−2，−32）． 【点睛】本题主要考查位似变换中对应点的坐标的变化规律．13． 【解析】【分析】利用点B 和点D 的坐标之间的关系得到线段AB 缩小2.5倍得到线段CD ，然后确定C 点坐标．【详解】解：∵将线段AB 缩小得到线段CD ，点B （5，0）的对应点D 的坐标为（2.0）， ∴线段AB 缩小2.5倍得到线段CD ，∴点C 的坐标为（1，2）．【点睛】本题考查了位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标的比等于k 或-k ．14．46（，）【解析】【分析】观察点B 点和B ′点的坐标得到位似比为2，然后根据此规律确定A ′的坐标.【详解】∵'OB BB =，∴1'2OB OB =∴位似比为2，∵A 的坐标是()23，， ∴点A '的坐标为()46，故答案是：()46，【点睛】本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．15．(4,4),(8,10),(10,4)A B C '''---或(4,4),(8,10),(10,4)A B C '''---【解析】【分析】把点A 、B 、C 的横纵坐标分别乘以2或﹣2即可．【详解】把点A 、B 、C 的横纵坐标分别乘以2得：A ′（4，－4），B ′（8，－10），C ′（10，－4）；把点A 、B 、C 的横纵坐标分别乘以﹣2得：A ′（－4，4），B ′（－8，10），C ′（－10，4）． 故答案为：A ′（4，－4），B ′（8，－10），C ′（10，－4）或A ′（－4，4），B ′（－8，10），C ′（－10，4）．【点睛】本题考查了位似变换．掌握以原点为位似中心的图形的坐标特点是解答本题的关键． 16．8【解析】【分析】根据位似图形面积比等于位似比的平方，知道其中一个面积，就可以求出另外一个面积.【详解】位似图形面积比等于位似比的平方，位似比是1:2，所以面积比是1:4，已知△ABC 的面积是2，则△DEF 的面积是8故答案为8【点睛】此题重点考察学生对位似图形面积的计算，抓住面积比等于位似比的平方是解题的关键.17．32【解析】【分析】当DE ⊥CE 时，DE 的有最小值，根据等腰直角三角形的性质和相似三角形的性质即可得到结论．【详解】当DE ⊥CE 时，DE 的有最小值．连接CE ．∵△BAC 和△EBP 是等腰直角三角形，∴∠EBC +∠CBP =∠CBP +∠PBA =45°，BC =2BA ，BE =2BP ，∴∠EBC =∠PBA ，2BE BC BP BA==，∴△EBC ∽△PBA ，∴∠ECB =∠P AB ． ∵△BAC 是等腰直角三角形，AD ⊥BC ，∴∠P AB =45°，BD =DC =AD ，∴∠ECD =45°． ∵∠DEC =90°，∴△DEC 是等腰直角三角形，∴DC =2DE =32，∴AD =32． 故答案为：32．【点睛】本题考查了相似三角形的判定与性质以及等腰直角三角形的性质，熟练掌握相似三角形的判定与性质是解题的关键．18．（-2，0）【解析】【分析】利用如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心，进而得出位似中心．【详解】解：如图所示：点P（-2，0）即为所求．故答案为：（-2，0）．【点睛】本题考查位似变换，根据题意得出位似中心的位置是解题的关键．19．1,22⎛⎫- ⎪⎝⎭【解析】【分析】通过把位似中心平移到原点，利用关于以原点为位似中心的对应点的坐标规律求解．【详解】把△ABC向下平移1个单位得到A点的对应点的坐标为（1，﹣2），点（1，﹣2）以原点为位似中心，在位似中心两侧的对应点的坐标为（12-，1），把点（12-，1）先上平移1个单位得到（12-，2），所以D点坐标为（12-，2）．故答案为：（12-，2）．【点睛】本题考查了位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k．20．（1）CE＝245，CG＝185，（2）CE＝5，CG＝154；（3）结论：△EBG是直角三角形．理由见解析.【解析】【分析】（1）利用面积法求出CE，再利用勾股定理求出EF即可；（2）利用直角三角形斜边中线定理求出CE，再利用相似三角形的性质求出EF即可；（3）根据直角三角形的判定方法：如果一个三角形一边上的中线等于这条边的一半，则这个三角形是直角三角形即可判断．【详解】解：（1）如图2中，在Rt△BAD中，BD＝22AD AB+＝10，∵S△BCD＝12•CD•BC＝12•BD•CE，∴CE＝245．CG＝BE＝222465⎛⎫- ⎪⎝⎭＝185，（2）如图3中，过点E作MN⊥AM交AB于N，交CD于M．∵DE＝BE，∴CE＝12BD＝5，∵△CME∽△ENF，∴CM EN CE EF=，∴CG＝EF＝154．（3）结论：△EBG是直角三角形．理由：如图1中，连接BH．在Rt△BCF中，∵FH＝CH，∴BH＝FH＝CH，∵四边形EFGC是矩形，∴EH＝HG＝HF＝HC，∴BH＝EH＝HG，∴△EBG是直角三角形．【点睛】四边形的综合题，主要考查矩形的性质、相似三角形的判定和性质、勾股定理、直角三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造相似三角形或直角三角形解决问题．21．（1）作图见解析；（2）7.5．【解析】【分析】（1）由于每个小正方形边长为1，先利用勾股定理求出△ABC的三边分别为AB=5，BC=2，AC=5，DE=5，根据三边对应成比例的两三角形相似，可以画出格点△DEF，使DF=5，EF=10；（2）根据三角形的面积公式求解即可．【详解】（1）如图所示，△DEF与△ABC相似；（2）△DEF 的面积=12×5×3=7.5． 【点睛】 本题考查了利用相似变换作图，勾股定理，相似三角形的判定，三角形的面积，熟练掌握网格结构，根据相似比准确找出对应点的位置是解题的关键．22．（1）详见解析；②AE ，理由详见解析；（2）AE ﹣BE ；（3）或DE=2AEBE ．【解析】【分析】（1）①由正方形的性质得到AD ＝AB ，∠BAD ＝90°，判断出△ABE ≌△ADF ，即可；②由①得到△ABE ≌△ADF ，并且判断出△EAF 为直角三角形，用勾股定理即可；（2）先由正方形的性质和已知条件判断出△ABE ≌△ADF ，再用判断出△EAF 为直角三角形，用勾股定理即可；（3）分两种情况讨论，先由正方形的性质和已知条件判断出△ABE ∽△ADF ，AF，DF，再判断出△EAF 为直角三角形，用勾股定理结合图形可得结论．【详解】（1）①正方形ABCD 中，AD=AB ，∠ADM+∠AMD=90°∵BE ⊥DP ，∴∠EBM+∠BME=90°，∵∠AMD=∠BME ，∴∠EBM=∠ADM ，在△ABE 和△ADF 中，FAD EAB EBM ADM AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△ADF ，∴DF=BE ；②，理由：由（1）有△ABE ≌△ADF ，∴AE=AF，∠BAE=∠DAF，∴∠BAE+∠FAM=∠DAF+∠FAM，∴∠EAF=∠BAD=90°，∴EF=2AE，∵DE=DF+EF，∴DE=BE+2AE；（2）DE=2AE﹣BE；理由：正方形ABCD中，AD=AB，∠BAD=∠BAE+∠DAE=90°，∵∠FAD=∠EAB，∴∠EAF=∠BAD=90°，∴∠AFE+∠AEF=90°∵BE⊥DP，∴∠BEA+∠AEF=90°，∴∠BEA=∠AFE，∵∠FAD=∠EAB，AD=AB∴△ABE≌△ADF，∴AE=AF，BE=DF∵∠EAF=90°∴EF=2AE，∵EF=DF+DE=2AE，∴DE=2AE﹣DF=2AE﹣BE；（3）DE=2AE+3BE或DE=2AE﹣3BE．①如图1所示时，正方形ABCD 中，∠ADM+∠AMD=90° ∵BE ⊥DP ，∴∠EBM+∠BME=90°，∵∠AMD=∠BME ，∴∠EBM=∠ADM ，∵∠FAD=∠EAB∴△ABE ∽△ADF ，∴AB AE BE AD AF DF==， ∵AD ：AB=3：1，∴3AE BE AF DF ==， ∴AF=3AE ，DF=3BE∵∠FAD=∠EAB∴∠EAF=∠EAB+∠BAF=∠FAD+∠BAF=∠BAD=90°，∴EF=22AE AF +=2AE=DE ﹣DF=DE ﹣3BE ，即：DE=2AE+3BE ；②如图2所示，∵∠DAF=∠BAE ，∴∠EAF=∠BAD=90°，∵∠DAF=∠BAE ，∴△BAE ∽△DAF ，∴AB AE BE AD AF DF==，∵AD ：AB=3：1，∴3AE BE AF DF ==， ∴AF=3AE ，DF=3BE ，∵∠EAF=90°，根据勾股定理得，EF=22AE AF +=2AE=DE+DF=DE+3BE ，∴DE=2AE ﹣3BE ．【点睛】此题是四边形的综合题，主要考查了正方形的性质，矩形的性质，全等三角形的性质和判定，相似三角形的性质和判定，勾股定理，解本题的关键是用勾股定理得到线段的关系． 23．(1)见解析；（2）2：1【解析】【分析】（1）运用相似的原理，进行图形的扩大或者缩小变换，要求熟练掌握相似作图．（2）利用相似三角形对应边的比值即是相似比求出即可．【详解】(1)利用三角形相似作图,连接OA,OB,OC,分别找出这三条线段的中点A′、B′、C′,顺次连接A′、B′、C′即可得到△A′B′C′；如图所示：(2)根据相似三角形的性质，因为ABC ∆与A B C '''∆是相似三角形，且BC:B′C′=2:1，故答案为2:1.【点睛】本题考查作图-位似变换，解题的关键是掌握相似三角形的性质.24．（1）132；（2）见解析；（3）见解析，3；（4）见解析.【解析】 【分析】 （1）利用分割法取三角形面积即可．（2）利用三角形中位线定理，分别取PA ，AB 的中点E ，F 即可．（3）利用数形结合的思想，根据三角形的面积公式以及平行线间的距离相等解决问题即可． （4）过点B 作BJ ⊥C 1C 2于点M ，过点A 作BN ⊥C 1C 2于点N ，可得矩形ABMN ．【详解】解：（1）S △PAB ＝4×4﹣12×1×4﹣12×4×3﹣12×1×3＝132． 故答案为132. （2）△PEF 如图①中所示．∵CD=PD,DE ∥AC,∴AE=PE,即E 是AP 的中点，同理可证F 是AB 的中点，∴EF 是△ABP 的中位线，∴△AEF 与△PAB 相似比为1：2；（3）满足条件的点C 如图所示，有3个.S △ABC1=11143622AC BH ⨯=⨯⨯=, 同理可求△ABC 2的面积=6，∴C 1C 2∥AB ，∴△△ABC 3的面积=6，故答案为3．（4）矩形ABMN如图②中所示．过点B作BJ⊥C1C2于点M，过点A作BN⊥C1C2于点N，∵△ABC1的面积=6，∴矩形ABMN的面积=12.【点睛】本题考查了作图-位似变换，平行线分线段成比例定理，三角形的中位线，矩形的判定和性质，三角形的面积等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．25．（1）见解析；（2）见解析.【解析】【分析】（1）根据旋转的性质及方格纸的特点找出对应点，然后连接即可；（2）根据位似的性质及方格纸的特点找出对应点，然后连接即可【详解】解：（1）如图；（2）如图.【点睛】本题考查了旋转的性质，以及位似的性质，熟练掌握性质是解答本题的关键.旋转的性质：对应顶点到旋转中心的距离相等，对应点与旋转中心的夹角等于旋转角. 位似图形的性质，①位似图形的任意一对对应点与位似中心在同一直线上，它们到位似中心的距离之比等于相似比.26．（1）y＝﹣34x+3（2）当x＝45时，QP∥BE，而QB与PE不平行，此时四边形PQBE是梯形（3）当x＝43或x＝2013或x＝2827或x＝83时，△PQE为等腰三角形【解析】【分析】（1）由四边形ABCD为矩形，得到∠D为直角，对边相等，可得三角形ADC为直角三角形，由AD与DC的长，利用勾股定理求出AC的长，再由PE平行于CD，利用两直线平行得到两对同位角相等，可得出三角形APE与三角形ADC相似，由相似得比例，将各自的值代入，整理后得到y与x的关系式；（2）若QB与PE平行，得到四边形PQBE为矩形，不合题意，故QB与PE不平行，当PQ 与BE平行时，利用两直线平行得到一对内错角相等，可得出一对邻补角相等，再由AD与BC平行，得到一对内错角相等，可得出三角形APQ与三角形BEC相似，由相似得比例列出关于x的方程，求出方程的解即可得到四边形PQBE为梯形时x的值；（3）存在这样的点P和点Q，使P、Q、E为顶点的三角形是等腰三角形，分两种情况考虑：当Q在AE上时，由AE﹣AQ表示出QE，再根据PQ＝PE，PQ＝EQ，PE＝QE三种情况，分别列出关于x的方程，求出方程的解即可得到满足题意x的值；当Q在EC上时，由AQ ﹣AE表示出QE，此时三角形为钝角三角形，只能PE＝QE列出关于x的方程，求出方程的解得到满足题意x的值，综上，得到所有满足题意的x的值．【详解】（1）∵矩形ABCD，∴∠D＝90°，AB＝DC＝3，AD＝BC＝4，∴在Rt△ACD中，利用勾股定理得：AC5，∵PE∥CD，∴∠APE＝∠ADC，∠AEP＝∠ACD，∴△APE∽△ADC，又PD＝x，AD＝4，AP＝AD﹣PD＝4﹣x，AC＝5，PE＝y，DC＝3，∴AP AE PEAD AC DC==，即4453x AE y-==，∴y＝﹣34x+3；（2）若QB∥PE，四边形PQBE是矩形，非梯形，故QB与PE不平行，当QP∥BE时，∠PQE＝∠BEQ，∴∠AQP＝∠CEB，∵AD∥BC，∴∠PAQ＝∠BCE，∴△PAQ∽△BCE，由（1）得：AE＝﹣54x+5，PA＝4﹣x，BC＝4，AQ＝x，∴PA AQ AQBC CE AC AE==-，即445455(5)4x x xxx-==--+，整理得：5（4﹣x）＝16，解得：x＝45，∴当x＝45时，QP∥BE，而QB与PE不平行，此时四边形PQBE是梯形；（3）存在．分两种情况：当Q在线段AE上时：QE＝AE﹣AQ＝﹣54x+5﹣x＝5﹣94x，（i）当QE＝PE时，5﹣94x＝﹣34x+3，解得：x＝43；（ii）当QP＝QE时，∠QPE＝∠QEP，∵∠APQ+∠QPE＝90°，∠PAQ+∠QEP＝90°，∴∠APQ＝∠PAQ，∴AQ＝QP＝QE，∴x＝5﹣94x，解得：x＝20 13；（iii）当QP＝PE时，过P作PF⊥QE于F，可得：FE＝12 QE＝12（5﹣94x）＝2098x-，∵PE∥DC，∴∠AEP＝∠ACD，∴cos∠AEP＝cos∠ACD＝35CDAC=，∵cos∠AEP＝FEPE＝2098334xx--+＝35，解得：x＝2827；当点Q在线段EC上时，△PQE只能是钝角三角形，如图所示：∴PE＝EQ＝AQ﹣AE，AQ＝x，AE＝﹣54x+5，PE＝﹣34x+3，∴﹣34x+3＝x﹣（﹣54x+5），解得：x＝83．综上，当x＝43或x＝2013或x＝2827或x＝83时，△PQE为等腰三角形．【点睛】此题属于相似综合题，涉及的知识有：矩形的性质，勾股定理，相似三角形的判定与性质，平行线的性质，梯形的判定，以及等腰三角形的性质，利用了数形结合及分类讨论的数学思想，分类讨论时要做到不重不漏，考虑问题要全面．27．（1）见解析；（2）坐标为（-2a，-2b）【解析】【分析】（1）依据以原点O为位似中心，△A1B1C1与△ABC的位似比为2：1作图即可；【详解】解：（1）如图所示，以原点O为位似中心，△A1B1C1与△ABC的位似比为2：1，则△AB1C1即为所求；（2）如图所示，∵P（a，b）为线段AC上的任意一点，点P，P1以原点O为位似中心，∴点P1在线段A1C1上，并且P1坐标为：（-2a，-2b）.【点睛】本题主要考查了利用轴对称变换以及位似变换进行作图．。

一、选择题1．如图，ABC 的两个顶点B 、C 均在第一象限，以点()0,1A 为位似中心，在y 轴左侧作ABC 的位似图形ADE ，ABC 与ADE 的位似比为1：2若点C 的纵坐标是m ，则其对应点E 的纵坐标是（ ）A ．32m -+B ．23m +C ．()23m -+D ．23m -+ 2．点B 把线段AC 分成两部分，如果BC AB AB AC =＝k ，那么k 的值为（ ） A ．512+ B ．512- C ．5＋1 D ．5－1 3．如图，在▱ABCD 中，E 是BC 的中点，DE ，AC 相交于点F ，S △CEF ＝1，则S △ADC ＝（ ）A ．3B ．4C ．5D ．64．如图，在▱ABCD 中，点O 是对角线BD 上的一点，且12OD OB =，连接CO 并延长交AD 于点E ，若△COD 的面积是2，则四边形ABOE 的面积是（ ）A ．3B ．4C ．5D ．65．如图，已知□ABCD ，以B 为位似中心，作□ABCD 的位似图形□EBFG ，位似图形与原图形的位似比为23，连结CG ，DG ．若□ABCD 的面积为30，则△CDG 的面积为（ ）A ．3B ．4C ．5D ．6 6．如图，CD ，BE 分别是ABC 两条中线，连结DE ，则:EDC ABC S S 的比值是（ ）A ．12B ．14C ．13D ．237．如图，在矩形ABCD 中，E ，F 分别为BC ，CD 的中点，线段AE ，AF 与对角线BD 分别交于点G .设矩形ABCD 的面积为S ，则下列结论不正确的是（ ）A ．:2:1AG GE =B ．::1:1:1BG GH HD =C ．12313S S S S ++=D ．246::1:3:4S S S = 8．若34,x y =则x y =（ ） A ．34 B ．74 C ．43 D ．739．如图，已知ABC ，DCE ，FEG ，HGI 是四个全等的等腰三角形，底边BC ，CE ，EG ，GI 在同一直线上，且4AB =，2BC =，连接AI 交FG 于点Q ，则QI 的值为（ ）A ．4B ．103C ．3D ．8310．如图，梯形ABCD 中，AC 交BD 于点O ，已知AD ∥BC ，AD =2，BC =4，S △AOD =1，则梯形ABCD 的面积为（ ）A ．9B ．8C ．7D ．611．如图，在Rt ABC 中，90ACB ∠=︒，以其三边为边向外作正方形，过点C 作CR FG ⊥于点R ，再过点C 作PQ CR ⊥分别交边DE ，BH 于点P ，Q ．若2QH PE =，9PQ =，则CR 的长为（ ）A ．14B ．9C ．425D ．36512．如图，正方形ABCD 的边长为2，BE CE =， 1.MN =线段MN 的两端在CD ，AD 上滑动，当ABE 与以D ，M ，N 为顶点的三角形相似时，DM 的长为（ ）A ．13B ．13或23C ．55D ．55或255二、填空题13．如图，正方形ABCD 中，BE ＝EF ＝FC ，CG ＝2GD ，BG 分别交AE ，AF 于M ，N ．下列结论：①AF ⊥BG ；②BN ＝32NF ；③38BM MG =；④S 四边形CGNF ＝12S 四边形ANGD ，其中正确的结论的序号是_____．14．如图，小静在横格纸上画了两条线段AB ，CD ，点A ，D 在同一条格线上，点B ，C 在同一条格线上，AB 与CD 的交点也在格线上，横格纸的横线平行且相邻横线间的距离相等，若4=AD ，则BC =______．15．如图，在ABC ∆中，点111,,A B C 分别是,,AC BC AB 的中点，连接1111,AC A B ，四边形111A B BC 的面积记作1S ；点222,,A B C 分别是1111,,A C B C A B 的中点，连接2222,A C A B ，四边形2212A B B C 的面积记作2S …，按此规律进行下去，若ABC S a ∆=，则3S =__________；n S =__________．（n 为正整数）16．如图，在矩形ABCD 中，E 是边AB 的中点，连接DE 交对角线AC 于点F ，若AB ＝4，AD ＝3，则CF 的长为_____．17．已知AEF ABC ∽，且:1:3AE AB =，四边形EBCF 的面积是8，则ABC S =____________．18．如图，在正方形ABCD 中，对角线,AC BD 相交于点,O E 是OB 的中点，连接AE 并延长交BC 于点,F 若BEF ∆的面积为1,则正方形ABCD 的面积为________________________．19．线段AB 、CD 在平面直角坐标系中的网格位置，如图所示，O 为坐标原点，A 、B 、C 、D 均在格点上，线段AB 、CD 是位似图形，位似中心的坐标是__________．20．《九章算术》中记载了一种测量井深的方法．如图所示，在井口B 处立一根垂直于井口的木杆BD ，从木杆的顶端D 观察井水水岸C ，视线DC 与井口的直径AB 交于点E ，如果测得AB ＝1.8米，BD ＝1米，BE ＝0.2米，那么井深AC 为____米．三、解答题21．如图，上体育课时，甲、乙两名同学分别站在C 、D 的位置时，乙的影子恰好在甲的影子里边，已知甲，乙同学相距1米．甲身高1.8米，乙身高1.5米，则甲的影长是多少米？22．如图，直角坐标系xOy 中，一次函数+6y x =-的图象1l 分别与,x y 轴交于,A B 两点，正比例函数的图象2l 与1l 交于点(),5C m（1）求m 的值及2l 的解析式；（2）求AOC S 的值；（3）垂直于x 轴的直线x a =与直线12,l l 分别交于点,P Q ，若线段2PQ =，求a 的值； （4）一次函数64y kx k =-+的图象与线段AB （含端点）有公共点，且满足y 随x 的增大而减小，设直线与x 轴的交点横坐标为,x 直接写出x 的取值范围．23．如图，在矩形ABCD 中，E 是BC 上一点，DF AE ⊥于点F ，设()0AD AEλλ=>．（1）若1λ=，求证：CE FE =；（2）若3,4AB AD ==，且D B F 、、在同一直线上时，求λ的值．24．如图，在△ABC 中，∠C =∠ADE ，AB =3，AD =2，CE =5，求证：（1）△ADE ∽△ACB ；（2）求AE 的长．25．如图，小明想测量河对岸建筑物AB 的高度，在地面上C 处放置了一块平面镜，然后从C 点向后退了2.4米至D 处，小明的眼睛E 恰好看到了镜中建筑物A 的像，在D 处做好标记，将平面镜移至D 处，小明再次从D 点后退2.52米至F 处，眼睛G 恰好又看到了建筑物顶端A 的像，已知小明眼睛距地面的高度ED ，GF 均为1.6米，求建筑物AB 的高度．（注：图中的左侧α，β为入射角，右侧的α，β为反射角）26．如图1，在等边ABC 中，点D 是BC 边上的动点（不与点B 、C 重合），点E 、F 分别在AB 和AC 边上，且EDF=60．（1）求证：BDE CFD △∽△；（2）若点D 移至BC 的中点，如图2，求证：FD 平分EFC ∠．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】设点C 的纵坐标为m ，然后表示出AC 、EA 的纵坐标的距离，再根据位似比列式计算即可；【详解】设点C 的纵坐标为m ，则A 、C 间的纵坐标的长度为()1m -，∵△ABC 放大到原来的2倍得到△ADE ，∴E 、A 间的纵坐标的长度为()21m -,∴点E 的纵坐标为()()2112323m mm ⎡⎤---=--=-+⎣⎦；故答案选D ．【点睛】 本题主要考查了位似变换，坐标与图形的性质，准确分析计算是解题的关键． 2．B解析：B【分析】设AC=1，由题意得AB=k ，BC=2k ，由AC=AB+ BC=1得到关于k 的一元二次方程，解方程即可．【详解】设AC=1， ∵BC AB AB AC==k ，且0k >， ∴AB=k ，BC=2k ，∵AC=AB+ BC=1，∴21k k +=，即210k k +-=，∵1a =，1b =，1c =-，()224141150b ac =-=-⨯⨯-=>，∴k =负值舍去)，∴12k =， 故选：B ．【点睛】本题考查了比例线段，公式法解一元二次方程，由比例线段得到一元二次方程是解题的关键．3．D解析：D【分析】根据已知可得△CEF ∽△ADF ，及EF 和DF 的关系，从而根据相似三角形的性质和三角形的面积得到答案．【详解】解：∵四边形ABCD 是平行四边形∴AD=BC ，△CEF ∽△ADF ， ∴EC EF AD DF= ∵E 是BC 的中点，∴EC=1122BC AD = ∴12EC EF AD DF == ∴2211()()24CEF ADF S EF S DF ∆∆=== ∵S △CEF ＝1，∴S △ADF ＝4， ∵12EF DF = ∴DF=2EF ∴S △D CF ＝2 S △CEF ＝2，∴S △ADC ＝S △ADF + S △D CF =4+2=6故选：D ．【点睛】本题主要考查了相似三角形的判定与性质，熟练掌握相似三角形的面积比等于相似比的平方是解答此题的关键．4．C解析：C【分析】由题意可得△BOC 的面积为4，通过证明△DOE ∽△BOC ，可求S △DOE ＝1，即可求解．【详解】解：∵12 ODOB，△COD的面积是2，∴△BOC的面积为4，∵四边形ABCD是平行四边形，∴AD∥BC，S△ABD＝S△BCD＝2＋4＝6，∴△DOE∽△BOC，∴DOEBOCSS.（ODOB）2＝14，∴S△DOE＝1，∴四边形ABOE的面积＝6﹣1＝5，故选：C．【点睛】本题主要考查了相似三角形的判定与性质，准确计算是解题的关键．5．C解析：C【分析】连接BG，根据位似变换的概念得到点D、G、B在同一条直线上，FG∥CD，根据相似三角形的性质得到BGBD＝FGCD＝23，根据三角形的面积公式计算，得到答案．【详解】解：连接BG，∵▱ABCD和▱EBFG是以B为位似中心的位似图形，∴点D、G、B在同一条直线上，FG∥CD，∵四边形ABCD是平行四边形，面积为30，∴△CDB的面积为15，∵FG∥CD，∴△BFG∽△BCD，∴BGBD＝FGCD＝23，∴DGBD＝13，∴△CDG的面积＝15×13＝5，故选：C．【点睛】本题考查的是位似变换的概念和性质、平行四边形的性质，掌握位似图形是相似图形、对应点的连线都经过同一点、对应边平行是解题的关键．6．B解析：B【分析】利用三角形中位线定理证明三角形的相似，根据相似三角形的性质确定面积之比，利用中线的性质等量代换三角形即可得证．【详解】∵CD ，BE 分别是ABC 两条中线，∴DE ∥BC ，DE=12BC ， ∴△ADE ∽△ABC ，∴ADE S =14ABC S , ∴ADE S：ABC S =1：4， ∵点E 是AC 的中点， ∴ADE S=EDC S ， ∴EDC S ：ABC S =1：4， 故选B ．【点睛】本题考查了三角形的中位线定理，三角形相似的判定与性质，中位线的性质，熟练掌握定理，灵活运用性质，规范进行代换是解题的关键．7．D解析：D【分析】 根据平行线分线段成比例定理和线段中点的定义得：21AG AD GE BE ==，可判断选项A 正确；同理根据平行线分线段成比例定理得：13BG BD =，13DH BD =即可判断B 选项；设1S x =根据相似三角形面积的比等于相似比的平方，等底同高三角形面积的关系依次用x 表示各三角形的面积，即可判断C 和D 选项．【详解】 ①四边形ABCD 是矩形,//BC AD BC AD ∴=点E 是BC 的中点1122//BE BC AD AD BE∴== ∴21AG AD GE BE == 故选项A 正确；②//BE AD1213BG BE DG AD BG BD ∴==∴= 同理得：13DH BD =::1:1:1BG GH HD BG GH HD ∴==∴=故选项B 正确 ③//BE ADDAG ∴△BEG ∽△ 13453414S S S BG GH HD S S S ∴=+==∴==设1S x =则5342S S S x ===12S x ∴=同理可得：2S x =1231243S S S x x x x S ∴++=++== 故选项C 正确；④由③可知：664S x x x x =--=246::1:2:4S S S ∴=故选项D 错误；故选：D ．【点睛】本题考查了矩形的性质,三角形相似的性质和判定,平行线分线段成比例定理,三角形面积等知识,解题的关键是理解题意,掌握等底同高三角形面积相等,相似三角形面积的比等于相似比的平方．8．C解析：C【分析】根据比例的性质，两内项之积等于两外项之积进行计算即可求解．【详解】由比例的性质，由34,x y =得43x y =． 故选C ． 【点睛】本题考查了比例的性质，利用比例的性质是解题关键． 9．D解析：D【分析】先求出BP ，进而利用勾股定理求出AP 的平方，即可求AI=8，最后判断出QG ∥AC ，即可通过全等得出结论．【详解】解：如图，过点A 作AP ⊥BC 垂足为P ，∵AB=AC ，BC=2，∴BP=12BC ＝1，BC=CE=EG=GI=2， 在Rt △ABP 中，根据勾股定理得，AP 2=AB 2-BP 2= 42-12=15 ，在Rt △API 中，PI=772BC =，根据勾股定理得222=1578AI AP PI ++= ， ∵△ABC ，△DCE ，△FEG ，△HGI 是4个全等的等腰三角形，∴∠ACB=∠QGC ，∴QG ∥AC ，∴△IGQ ∽△ICA ， ∴QI IG AI IC ＝ ， ∴268QI ＝， ∴QI=83， 故选：D ．【点睛】 此题主要考查了相似三角形的判定和性质，全等三角形的性质，平行线的判定和性质，勾股定理，等腰三角形的性质，求出AI 是解本题的关键．10．A解析：A【分析】先根据AD ∥BC ，得到△AOD ∽△COB ，从而得出△COB 的面积，再根据△AOB 与△COB 等高，从而得出△AOB 的面积，同理得出△DOC 的面积即可得出梯形ABCD 的面积．【详解】解：∵AD ∥BC ，∴△AOD ∽△COB∵AD =2，BC =4， ∴12AD BC = ∴114AOD COB COB S S S == ∴COB S △ =4∵△AOB 与△COB 等高，又∵12AO CO = ∴142AOB AOB COB S S S == ∴AOB S =2同理，DOC S =2∴ABCD S 梯形=AOD COB AOB DOC SS S S +++ =1+4+2+2=9．故选：A ．【点睛】 本题主要考查了相似三角形的性质，解题的关键是熟练掌握相似三角形的面积比等于相似比的平方．11．C解析：C【分析】连接EC ，CH ，设AB 交CR 于点J ，先证得△ECP ∽△HCQ ，可得12PC CE EP CQ CH HQ ===，进而可求得CQ ＝6，AC :BC ＝1:2，由此可设AC ＝a ，则BC ＝2a ，利用AC ∥BQ ，CQ ∥AB ，可证得四边形ABQC 为平行四边形，由此可得AB ＝CQ ＝6，再根据勾股定理求得AC =，5BC =125CJ =，进而可求得CR 的长． 【详解】解：如图，连接EC ，CH ，设AB 交CR 于点J ，∵四边形ACDE ，四边形BCIH 都是正方形，∴∠ACE ＝∠BCH ＝45°，∵∠ACB ＝90°，∠BCI ＝90°，∴∠ACE ＋∠ACB ＋∠BCH ＝180°，∠ACB ＋∠BCI ＝180°，∴点E 、C 、H 在同一直线上，点A 、C 、I 在同一直线上，∵DE ∥AI ∥BH ，∴∠CEP ＝∠CHQ ，∵∠ECP ＝∠QCH ，∴△ECP ∽△HCQ ， ∴12PC CE EP CQ CH HQ ===， ∵PQ ＝9，∴PC ＝3，CQ ＝6，∵EC :CH ＝1:2，∴AC :BC ＝1:2，设AC ＝a ，则BC ＝2a ，∵PQ ⊥CR ，CR ⊥AB ，∴CQ ∥AB ，∵AC ∥BQ ，CQ ∥AB ，∴四边形ABQC 为平行四边形，∴AB ＝CQ ＝6，∵222AC BC AB +=，∴2536a =，∴5a =（舍负）∴AC =，BC = ∵1122AC BC AB CJ ⋅⋅=⋅⋅，∴125565CJ ==， ∵JR ＝AF ＝AB ＝6，∴CR ＝CJ ＋JR ＝425， 故选择：C ．【点睛】本题考查了正方形的性质、相似三角形的判定及性质、平行四边形的判定及性质、勾股定理的应用，作出正确的辅助线并灵活运用相关图形的性质与判定是解决本题的关键． 12．D解析：D【分析】根据90B D ∠=∠=，所以只有两种可能，假设ABE △∽NDM 或ABE △∽MDN △，分别求出DM 的长即可．【详解】 解：正方形ABCD 边长是2，BE CE =，1BE ∴=，225AE AB BE ∴+=当ABE △∽NDM 时::DM BE MN AE ∴=，1.MN = 5DM ∴=． 当ABE △∽MDN △时，::DM BA MN AE ∴=，2=1，=AB MN25DM ∴ 5DM ∴=25． 故选D ．【点睛】本题考查相似三角形的判定与性质、正方形的性质．解决本题特别要考虑到①DM 与AB 是对应边时，②当DM 与BE 是对应边时这两种情况．二、填空题13．①②③【分析】由BE＝EF＝FCCG＝2GD可得BF=CG易证△ABF≌△BCG 即可解题；②易证△BNF∽△BCG即可求得的值即可解题；③作EH⊥AF令AB=3即可求得MNBM的值即可解题；④连接A解析：①②③【分析】由BE＝EF＝FC，CG＝2GD可得BF=CG，易证△ABF≌△BCG，即可解题；②易证△BNF∽△BCG，即可求得BNNF的值，即可解题；③作EH⊥AF，令AB=3，即可求得MN，BM的值，即可解题；④连接AG，FG，根据③中结论即可求得S四边形CGNF和S四边形ANGD，即可解题．【详解】解：①∵四边形ABCD为正方形，∴AB=BC=CD，∵BE=EF=FC，CG=2GD，∴BF=CG，∵在△ABF和△BCG中，90AB BCABF BCGBF CG⎧⎪∠∠︒⎨⎪⎩＝＝＝＝，∴△ABF≌△BCG，∴∠BAF=∠CBG，∵∠BAF+∠BFA=90°，∴∠CBG+∠BFA=90°，即AF⊥BG；①正确；②∵在△BNF和△BCG中，90CBG NBFBCG BNF∠∠⎧⎨∠∠︒⎩＝＝＝，∴△BNF∽△BCG，∴32BN BCNF CG==，∴BN=32NF；②正确；作EH⊥AF，令AB=3，则BF=2，BE=EF=CF=1，22AF AB BF=+13∵S △ABF =12AF•BN =12AB•BF ， ∴BN =61313，NF =23BN =41313， ∴AN =AF -NF =913， ∵E 是BF 中点，∴EH 是△BFN 的中位线，∴EH =313，NH =213，BN ∥EH ， ∴AH =111313，AN MN AH EH =，解得：MN =2713143， ∴BM=BN-MN =31311，MG=BG-BM =81311， ∴38BM MG =；③正确； ④连接AG ，FG ，根据③中结论，则NG=BG-BN 713 ∵S 四边形CGNF =S △CFG +S △GNF =12CG•CF +12NF•NG =1+1413=2713， S 四边形ANGD =S △ANG +S △ADG =12AN•GN +12AD•DG =6335126213+=， ∴S 四边形CGNF ≠12S 四边形ANGD ，④错误； 故答案为 ①②③．【点睛】本题考查了全等三角形的判定和性质，考查了相似三角形的判定和对应边成比例的性质，本题中令AB =3求得AN ，BN ，NG ，NF 的值是解题的关键．14．6【分析】过点O 作OE ⊥AD 于点EOF ⊥CB 于点F 则EOF 三点共线根据平行线分线段成比例可得代入计算即可解答【详解】解：如图过点O 作OE ⊥AD 于点EOF ⊥CB 于点F 则EOF 三点共线∵横格纸的横线平行解析：6【分析】过点O 作OE ⊥AD 于点E ，OF ⊥CB 于点F ，则E 、O 、F 三点共线，根据平行线分线段成比例可得AD OE BC OF=，代入计算即可解答． 【详解】解：如图，过点O 作OE ⊥AD 于点E ，OF ⊥CB 于点F ，则E 、O 、F 三点共线，∵横格纸的横线平行且相邻横线间的距离相等，∴AD OE BC OF =， 即423BC =， ∴CD=6．故答案为：6．【点睛】本题主要考查平行线分线段成比例，掌握平行线分线段所得线段对应成比例是解题的关键．15．【分析】根据三角形中位线定理结合相似三角形的判定和性质可求出S1的值进而可得出S2的值找出规律即可求值【详解】解：∵是的中位线∴∴∴同理∴；同理可得∴故答案为：；【点睛】本题考查的是相似三角形的性质 解析：a 32 212n a - 【分析】根据三角形中位线定理结合相似三角形的判定和性质可求出S 1的值，进而可得出S 2的值，找出规律即可求值．【详解】解：∵1111,AC A B 是ABC ∆的中位线，∴11111,//2AC BC AC BC =， ∴11AC A ABC ∆∆， ∴111144AC A ABC S S a ∆∆==，同理111144A CB ABC S S a ∆∆==，∴1111442S a a a a =--=； 同理可得，2335,,2232a a a S S ===， ∴212n n aS -=．故答案为：a 32；212n a - 【点睛】 本题考查的是相似三角形的性质及三角形中位线定理，正确得出面积变化规律是解答此题的关键．16．【分析】根据矩形的性质可得出AB ∥CD 进而可得出∠FAE ＝∠FCD 结合∠AFE ＝∠CFD （对顶角相等）可得出△AFE ∽△CFD 利用相似三角形的性质可得出＝＝2利用勾股定理可求出AC 的长度再结合CF ＝解析：103【分析】根据矩形的性质可得出AB ∥CD ，进而可得出∠FAE ＝∠FCD ，结合∠AFE ＝∠CFD （对顶角相等）可得出△AFE ∽△CFD ，利用相似三角形的性质可得出CF AF ＝CD AE ＝2，利用勾股定理可求出AC 的长度，再结合CF ＝CF CF AF +•AC ，即可求出CF 的长． 【详解】解：∵四边形ABCD 为矩形，∴AB ＝CD ，AD ＝BC ，AB ∥CD， ∴∠FAE ＝∠FCD ，又∵∠AFE ＝∠CFD ，∴△AFE ∽△CFD ，∴CF AF ＝CD AE＝2． ∵AC 22AB BC +5， ∴CF ＝CF CF AF+•AC ＝221+×5＝103． 故答案为：103． 【点睛】本题考查了矩形的性质、相似三角形的判定与性质以及勾股定理，利用相似三角形的性质找出CF=2AF 是解题的关键．17．9【分析】根据相似三角形性质得到△AEF 和△ABC 面积比为1∶9设列方程即可求解【详解】解：∵∴∴设则解得x=9故答案为：9【点睛】本题考查了相似三角形的性质根据相似三角形性质求出面积比设出未知数列解析：9【分析】根据相似三角形性质得到△AEF 和△ABC 面积比为1∶9，设ABC S x =△，列方程即可求解．【详解】解：∵AEF ABC ∽，:1:3AE AB =， ∴219AEF ABC S AE S AF ⎛⎫== ⎪⎝⎭△△, ∴设ABC S x =△， 则189x x -=， 解得x=9．故答案为：9【点睛】 本题考查了相似三角形的性质，根据相似三角形性质求出面积比，设出未知数列出方程是解题关键．18．【分析】根据正方形的性质得OB ＝ODAD ∥BC 根据三角形相似的性质和判定得：根据同高三角形面积的比等于对应底边的比可得结论【详解】解：∵四边形ABCD 是正方形∴OB ＝ODAD ∥BC ∴△BEF ∽△DE解析：24【分析】根据正方形的性质得OB ＝OD ，AD ∥BC ，根据三角形相似的性质和判定得：13BE EF ED AE ==，根据同高三角形面积的比等于对应底边的比，可得结论． 【详解】解：∵四边形ABCD 是正方形，∴OB ＝OD ，AD ∥BC ，∴△BEF ∽△DEA ， ∴BE EF ED AE=， ∵E 是OB 的中点， ∴13BE EF ED AE ==，∴S △BEF ：S △AEB ＝EF ：AE ＝13， ∵△BEF 的面积为1，∴△AEB 的面积为3，∵13BE ED ， ∴S △AEB ：S △AED ＝13， ∴△AED 的面积为9，∴S △ABD =9+3=12， ∴正方形ABCD 的面积=12×2=24．故答案为：24．【点睛】本题考查了正方形的性质，三角形面积，三角形相似的性质和判定等知识，熟练掌握相似三角形的性质和判定是关键．19．(00)或(4)【分析】分①点A 和点C 为对应点点B 和点D 为对应点；②点A 和点D 为对应点点B 和点C 为对应点两种情况根据位似中心的概念解答【详解】解：①当点A 和点C 为对应点点B 和点D 为对应点时延长CAB解析：(0，0)或(143，4) 【分析】分①点A 和点C 为对应点，点B 和点D 为对应点；②点A 和点D 为对应点，点B 和点C 为对应点两种情况，根据位似中心的概念解答．【详解】解：①当点A 和点C 为对应点，点B 和点D 为对应点时，延长CA 、BD 交于点O ，则位似中心的坐标是（0，0），②当点A 和点D 为对应点，点B 和点C 为对应点时，连接AD 、BC 交于点P ，则点P 为位似中心，∵线段AB 、CD 是位似图形，∴AB ∥CD ，∴△PAB ∽△PDC ，∴12AP AB PD CD ===，即152AP AP =-， ∴AP 53=， ∴位似中心点P 的坐标是(533+，4)，即(143，4)， 综上所述，位似中心点的坐标是(0，0)或(143，4)， 故答案为：(0，0)或(143，4)． 【点睛】 本题考查了位似图形的概念和性质、相似三角形的性质，掌握位似图形的概念是解题的关键．20．8【分析】根据相似三角形的判定和性质定理即可得到结论【详解】解：∵BD ⊥ABAC ⊥AB ∴BD ∥AC ∴△ACE ∽△BDE ∴∴∴AC=8（米）故答案为：8【点睛】本题考查了相似三角形的应用正确的识别图形解析：8【分析】根据相似三角形的判定和性质定理即可得到结论．【详解】解：∵BD ⊥AB ，AC ⊥AB ，∴BD ∥AC ，∴△ACE ∽△BDE ， ∴AC AE BD BE =， ∴ 1.80.210.2AC -=， ∴AC=8（米），故答案为：8．【点睛】本题考查了相似三角形的应用，正确的识别图形是解题的关键．三、解答题21．6米【分析】先根据DE ∥BC 得出△ADE ∽△ACB ，再根据相似三角形的对应边成比例求出AD 的值，由AC ＝AD+CD 得出结论．【详解】解：∵DE ∥BC ，∴△ADE ∽△ACB ， ∴DE BC ＝AD AC， 设AD ＝x ，则有1.51.8＝1x x +， 解得x ＝5． 甲的影长AC ＝1+5＝6米．答：甲的影长是6米．【点睛】本题考查了相似三角形的应用，根据题意判断出△ADE ∽△ACB 是解题的关键． 22．（1）1m =， 5y x =；（2）15AOC S =；（3）43a =或23a =；（4）18x ≥． 【分析】（1）由一次函数+6y x =-的图象1l 过点(),5C m ，可得+65m -=求出m ，设2l 的解析式为y kx =过点C(1,5)，求出k 即可；（2） 由y=0时，+60,6x x -==，OA=6，12AOC C S OA y =⋅； （3）当x a =时，与直线1l 交于点P （,6a a -），与直线2l 交于点Q （,5a a ），PQ=()562a a --=解之即可；（4）由一次函数64=-+y kx k 的图象横过定点(6,4) ，一次函数64=-+y kx k 的图象过B （0,6），13k =-，一次函数为163y x =-+ ，与x 轴交点，当18x ≥时即可． 【详解】解：（1）∵一次函数+6y x =-的图象1l 过点(),5C m ，∴+65m -=，∴1m =，设2l 的解析式为y kx =过点C ，∴k=5，∴2l 的解析式为5y x =；（2）一次函数+6y x =-与x 轴交点为A ，当y=0时，+60,6x x -==，∴OA=6， 11651522AOC C S OA y =⋅=⨯⨯=； （3）当x a =时，与直线1l 交于点P （,6a a -），与直线2l 交于点Q （,5a a ），PQ=()56612a a a --=-=，113a -=， 113a -=±， 43a =或23a =； （4）一次函数整理得()64y k x =-+，由64x y =⎧⎨=⎩， ∴一次函数64=-+y kx k 的图象横过定点(6,4) ，A （6,0），B （0,6），一次函数64=-+y kx k 的图象过B （0,6），∴646k -+=，∴13k =-，∴一次函数163y x =-+， ∴y=0，x=18，当18x ≥时一次函数64=-+y kx k 的图象与线段AB （含端点）有公共点且满足y 随x 的增大而减小．【点睛】本题考查直线解析式，三角形面积，两直线l 1，l 2与x=a 交点距离，一次函数64=-+y kx k 的图象与线段AB （含端点）有公共点范围问题，掌握待定系数法求直线解析式，三角形面积求法，会求两直线l 1，l 2与x=a 交点距离，一次函数64=-+y kx k 的图象与线段AB （含端点）有公共点范围方法是解题关键．23．（1）证明见解析；（2）1615 【分析】（1）根据矩形的性质可得，90//B AD BC AB CD AD BC ∠=︒==，，，，再根据已知条件DF AE ⊥，即可证明DFA ≌ABE △，则AF BE =，进而通过线段的和差关系求得；（2）由勾股定理求得BD 的长度，再由ABD △的面积求得AF 的长度，则可用勾股定理求得DF 的长度，则可得BF 的长度，再由DFA ≌ABE △，求得EB 的长度，在Rt ABE △中，根据勾股定理即可求得AE ，即可求得λ的值．【详解】（1）∵1λ=，∴1AD AE=， ∴AD AE =，又∵四边形ABCD 是矩形，∴90//B AD BC AB CD AD BC ∠=︒==，，，，∴DAF AEB ∠=∠，∵DF AE ⊥，∴90DFA B ∠=∠=︒，∴在DFA 和ABE △中，DFA B DAF AEB AD AE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴DFA ≌ABE △，∴AF BE =，∵=AE AD BC =，∴AE AF BC BE -=-， ∴CE FE =；（2）如图，D B F 、、三点共线，∵3,4AB AD ==，∴5BD ==，∵DF AE ⊥， ∴1122ABD S AB AD BD AF =⋅=⋅△， ∴341255AB AD AF BD ⋅⨯===，∴165DF ===， ∴169555BF BD DF =-=-=， ∵//AD BE ， ∴在ADF 和EBF △中，FAD FEB ADF EBF AFD EFB ∠=∠∠=∠∠=∠，，，∴ADF ∽EBF △， ∴AD DF EB BF=， 即164595EB=， ∴94EB =，∴154AE ===， ∴14161554AD AE λ===．【点睛】 本题考查了矩形的性质、三角形全等的判定和性质、三角形相似的判定和性质、勾股定理、三角形面积、相似比等，解答本题的关键是熟练掌握运用以上知识点，利用勾股定理求解线段的长．24．（1）见解析；（2）1【分析】（1）利用“两角法”进行证明；（2）利用（1）中相似三角形的对应边成比例来求AE 的长度．【详解】解：（1）证明：∵∠C =∠ADE ，∠A =∠A ，∴△ADE ∽△ACB（2）解：由（1）知，△ADE ∽△ACB ，AC AB∵AB =3，AD =2，CE =5， ∴253AE AE =+， 得：121,6AE AE ==-（舍去）∴AE 的长是1【点睛】本题考查了相似三角形的判定与性质．本题关键是要懂得找相似三角形，利用相似三角形的性质求解．25．32米【分析】易得△ABC ∽△EDC 以及△ABD ∽△GFD ，根据相似三角形的性质得到关于x 和y 的方程组，求解即可．【详解】解：设AB 为xm ，BC 为ym ，根据题意知，△ABC ∽△EDC ，有 1.62.4x y =①． △ABD ∽△GFD ，有 1.62.4 2.52x y =+②． 联立①②，得x ＝32．答：建筑物AB 的高度为32m ．【点睛】本题考查相似三角形的实际应用，掌握相似三角形的性质是解题的关键．26．（1）见解析 （2）见解析【分析】（1）根据等腰三角形的性质得到∠B=∠C ，根据三角形的内角和定理和平角的定义得到∠BED=∠CDF ，于是得到△BDE ∽△CFD ；（2）根据相似三角形的性质得到对应边成比例，等量代换得到比例式，判定相似三角形，最后根据相似三角形的性质得出FD 平分∠EFC ．【详解】解：（1）∵AB=AC=BC ，∴∠B=∠C=60°，∵∠BED=180°-∠B-∠BDE=120°-∠BDE ，∠CDF=180°-∠EDF-∠BDE=120°-∠BDE ，∴∠BED=∠CDF ，∴△BDE ∽△CFD ；（2）∵△BDE ∽△CFD ，CF DF∵点D是BC的中点，∴BD=CD，∴CD DE=CF DF∵∠EDF=∠C=60°，∴△DEF∽△CDF，∴∠DFE=∠CFD，∴FD平分∠EFC．【点睛】本题考查了相似三角形的判定和性质，等腰三角形的性质，熟练掌握相似三角形的判定和性质是解题的关键．。

一、选择题1．下列各组长度的线段（单位：cm ）中，成比例线段的是（ ） A ．2，3，4，5 B ．1，3，4，10 C ．2，3，4，6D ．1，5，3，122．已知△ABC 如图，则下列4个三角形中，与△ABC 相似的是（ ）A ．B ．C ．D ．3．已知ABC 的三边长是2，6，2，则与ABC 相似的三角形的三边长可能是（ ）A ．1，2，3B ．1，3， 22C ．1，3，62 D ．1，3，334．如图，A B C '''是ABC 以点О为位似中心经过位似变换得到的，若:1:2OA A A ''=，则A B C '''的周长与ABC 的周长比是（ ）A ．1：2B ．1：3C ．1：4D ．4：95．如图，在ABC 中，D ，E 分别是边AB ，BC 上的点，且//DE AC ，若BE ：CE=1:3，则DOEAOCSS:的值为（ ）A．13B．14C．19D．1166．如图，在ABC中，中线BE，CD相交于点O，连接DE，给出下列结论∶①12DEBC=；②12SS=△DOE△COB；③AD OEAB OB=；④13COEADCSS=△△；⑤23BDOBCOSS=△△．其中不正确的个数是（）A．1 B．2 C．3 D．47．如图，ABC中，90ABC∠=︒，点E在CB的延长线上，13BE AB=，过点E作ED AC⊥于D．若AD ED=，6AC=，则CD的长为（）A．1.5 B．2 C．2.5 D．48．如图，已知∠1＝∠2，那么添加一个条件后，仍不能判定△ABC与△ADE相似的是（）A．∠C＝∠AED B．∠B＝∠D C．AB BCAD DE=D．AB ACAD AE=9．已知30MAN∠=︒，点B在射线AM上，按以下步骤作图：①分别以A，B为圆心，大于12AB的长为半径画弧，两弧相交于P，Q两点；②作直线PQ，交射线AN于点C，连接BC；③以B为圆心，BA长为半径画弧，交射线AN于点D．根据以上作图过程及所作图形，下列结论中错误的是（）A ．60BCD ∠=︒B ．2AB AD AC = C ．4ABD CBA ∠=∠D ．23AD AB =10．如图，////DE FG BC ，若3DF FB =，则EC 与GC 的关系是（ ）A ．4EC GC =B ．3EC GC = C ．52EC GC =D ．2EC GC =11．如图，在ABC 中，D 、E 分别是AB 、BC 边上的点，连接DE 并延长，与AC 的延长线交于点F ，且3AD BD =，2EF DE =，若2CF =，则AF 的长为（ ）A ．5B ．6C ．7D ．812．如图，在四边形ABCD 中，如果ADC BAC ∠=∠，那么下列条件中不能判定ADC 和BAC 相似的是（ ）A ．DAC ABC ∠=∠B ．CA 是BCD ∠的平分线C ．AD DCAB AC= D ．2AC BC CD =⋅二、填空题13．如图是一张矩形纸片，E 是AB 的中点，把BCE ∆沿直线CE 对折，使点B 落在BD 上的点F 处，2AB =，则CB =__________．14．如图所示是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地面上形成阴影（圆形）的示意图．已知桌面的半径为0.8m ，桌面距离地面1m ，若灯泡距离地面3m ，则地面上阴影部分的面积为_________m 2（结果保留)π．15．△ABC ，△DEF 的条件如图所示，则n 的值是_____．16．如图，一组平行线L 1、L 2、L 3截两相交直线L 4、L 5，则AOED=____．17．如图，在平面直角坐标系中，点(0,6)A ，(8,0)B ，点C 是线段AB 的中点，过点C 的直线l 将AOB 截成两部分，直线l 交折线A O B --于点P ．当截成两部分中有三角形与AOB 相似时，则点P 的坐标为__________．18．如图，ABCD 中，E 是CD 的延长线上一点，BE 与AD 交于点F ，2CD DE =．若DEF 的面积为1，则ABCD 的面积为______．19．如图，在平行四边形ABCD 中，AC ，BD 相交于点O ，E 是OA 的中点，连接BE 并延长交AD 于点F ．（1）FDAF=__________； （2）若AEF 的面积为4，则平行四边形ABCD 的面积为__________．20．如图，在矩形ABCD 中，ABC ∠的平分线BE 与AD 交于点E ，BED ∠的平分线EF 与DC 交于点F ，若12AB =，2DF FC =，则BC 的长是_____．三、解答题21．如图，已知ADB A C ∠=∠+∠．（1）求证：CBDCAB ；（2）若1,2CD AD ==，求CB 的长．22．如图，在△ABC 中，点D 、E 分别在边AB 、AC 上，AED B ∠=∠，AG 分别交线段DE 、BC 于点F 、G ，且AD ：AC DF =：CG ， 求证：（1）AG 平分BAC ∠； （2）EF·CG=DF·BG ．23．问题发现：（1）如图1，在Rt ABC 中，90ABC ∠=︒，6AB =，8BC =，点D 为AB 上一点，且2AD DB =，过点D 作//DE BC ，填空：DE BC =________，DBEC=________； 类比探究：（2）如图2，在（1）的条件下将ADE 绕点A 逆时针旋转得到AMN ，连接DM ，BM ，EN ，CN ，请求出DM EN，BMCN 的值； 拓展延伸：（3）如图3，ABC 和DEF 同为等边三角形，且36AB EF ==，连接AD ，BE ，将DEF 绕AC （DF ）的中点O 逆时针自由旋转，请直接写出在旋转过程中BE AD -的最大值．24．综合问题：从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线． （1）如图1，在△ABC 中，CD 为角平分线，∠A =40°，∠B =60°，求证：CD 为△ABC 的完美分割线．（2）在△ABC 中，∠A =48°，CD 是△ABC 的完美分割线，且△ACD 为等腰三角形，求∠ACB 的度数．（3）如图2，△ABC 中，AC =2，DC =6-2，BD =31-，CD 是△ABC 的完美分割线，且△ACD 是以CD 为底边的等腰三角形，求CB 长．25．（1）如图1，矩形ABCD 中，点M 在BC 上，连接AM ，作AMN AMB ∠=∠，点N 在直线AD 上，MN 交CD 于点E ．请找出图1中的一个等腰三角形，并证明结论．（2）如图2，矩形ABCD 中，3AB =，2BC =，点M 为BC 中点，连接AM ，作AME AMB ∠=∠，ME 交于点E ，求CE 的长．26．如图，在平面直角坐标系中，已知ΔABC 三个顶点的坐标分别是A(-4，2)，B(-3，1)，C(-1，2)．（1）请画出ΔABC 关于x 轴对称的ΔA 1B 1C 1；（2）以点O 为位似中心，相似比为1：2，在y 轴右侧，画出ΔA 1B 1C 1放大后的ΔA 2B 2C 2；【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】判定四条线段是否成比例，计算前两条线段之比与后两条线段之比是否相等即可．【详解】解：A.2:3≠4:5，故四条线段不成比例，不合题意；B.1:3≠4:10，故四条线段不成比例，不符合题意；C.2:3=4:6，故四条线段成比例，符合题意；D.1:5≠3:12，故四条线段不成比例，不合题意；故选：C．【点睛】本题主要考查了成比例线段的定义，熟记概念并准确计算是解题的关键．2．C解析：C【分析】△ABC是等腰三角形，底角是75°，则顶角是30°，看各个选项是否符合相似的条件．【详解】解：∵由图可知，AB＝AC＝6，∠B＝75°，∴∠C＝75°，∠A＝30°，A、三角形各角的度数分别为75°，52.5°，52.5°，不符合题意；B、三角形各角的度数都是60°，不符合题意；C、三角形各角的度数分别为75°，30°，75°，符合题意；D、三角形各角的度数分别为40°，70°，70°，不符合题意；∴只有C 选项中三角形各角的度数与题干中三角形各角的度数相等， 故选：C ． 【点睛】此题主要考查等腰三角形的性质，三角形内角和定理和相似三角形的判定的理解和掌握，解题的关键是熟练掌握相似三角形的判定．3．A解析：A 【分析】根据相似三角形的判定定理即可得到结论． 【详解】解：∵△ABC ，2，∴△ABC：2=1 ∴△ABC相似的三角形三边长可能是1， 故选：A ． 【点睛】本题考查了相似三角形的判定，熟练掌握相似三角形的判定定理是解题的关键．4．B解析：B 【分析】根据位似变换的概念得到，A B ''∥AB ，A B C ABC '''∽△△，根据相似三角形的性质解答即可． 【详解】解：∵:1:2OA A A ''=， ∴13OA OA ':=:，∵A B C '''是ABC 以点O 为位似中心经过位似变换得到的， ∴A B ''∥AB ，A B C ABC '''∽△△， ∴13A B OA AB OA '''==， ∴A B C '''的周长与ABC 的周长比为1：3， 故选：B ． 【点睛】本题考查的是位似变换的概念和性质、相似三角形的性质，掌握位似的两个图形必须是相似形、对应边平行是解题的关键．5．D解析：D 【分析】由BE ：EC=1：3，得BE ：BC=1：4；证明△DOE ∽△AOC ，得到14DE BE AC BC ==，借助相似三角形的性质即可解决问题． 【详解】解：∵BE ：EC=1：3； ∴BE ：BC=1：4； ∵DE ∥AC ， ∴△DOE ∽△AOC ， ∴14DE BE AC BC ==， ∴21()16DOE AOC S DE S AC ∆∆==， 故选：D ． 【点睛】该命题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是灵活运用形似三角形的判定及其性质来分析、判断、推理或解答．6．B解析：B 【分析】根据中位线的性质，//DE BC ，通过证明DOE COB △∽△，得DOE COBS S；根据相似三角形性质，通过证明ADE ABC △△∽，证得AD OEAB OB=；结合点D 是AB 的中点，点E 是AC 的中点，通过三角形面积关系计算，即可得到COE ADC S S △△，同理计算得BDOBCOS S △△，即可得到答案． 【详解】根据题意得：点D 是AB 的中点，点E 是AC 的中点 ∴DE 是ABC 的中位线∴12DE BC =，即①结论正确； 又∵DE 是ABC 的中位线∴//DE BC∴DEO CBO ∠=∠，EDO BCO ∠=∠ ∴DOE COB △∽△∴12OE OD DE OB OC BC ===，214DOE COBSDE SBC ⎛⎫== ⎪⎝⎭，即②结论错误； 又∵//DE BC∴ADE ABC =∠∠，AED ACB ∠=∠ ∴ADE ABC △△∽∴12AD DE AB BC == ∴AD OE AB OB =，即③结论正确； ∵12OE OB = ∴13OE OE BE OB OE ==+ ∴13COE BEC S OE S BE ==△△ ∵点D 是AB 的中点，点E 是AC 的中点 ∴12ADC ABC S AD S AB ==△△，12BEC ABC S CE S AC ==△△ ∴111326COE COE BEC ABC BEC ABC S S S S S S =⨯=⨯=△△△△△△ ∴1632COE COEABC ADC S S S S ==△△△△，即④结论正确； ∵12OD DE OC BC == ∴12BDO BCO S OD S OC ==△△，即⑤结论错误； 故选：B ．【点睛】本题考查了三角形中位线、相似三角形、平行线的知识；解题的关键是熟练掌握三角形中位线、相似三角形的性质，从而完成求解．7．B解析：B【分析】证明△ADF ≌△EDC ，得到DC=DF ，设DC=x ，再证明△EBF ∽△ABC ，求出x 即可．【详解】解：∵∠ABC=90°，ED ⊥AC ，∴∠EBA=∠ADE=90°，又∠1=∠2，∴∠E=∠A ，∵AD=ED ，∴△ADF ≌△EDC ，∴DC=DF ，设DC=x ，∴DF=x ，∴AD=ED=6-x ，∴EF=6-2x ，∵∠E=∠A ，∠FBE=∠ABC ，∴△EBF ∽△ABC ， ∴BE EF AB AC =， ∵AC=6，BE=13AB ， ∴163EF =， ∴EF=6-2x=2，∴x=2，∴CD=2，故选B ．【点睛】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，解题的关键是掌握相应的判定方法，利用性质定理求出结果．8．C解析：C【分析】根据已知及相似三角形的判定方法对各个选项进行分析，从而得到最后答案．【详解】解：∵∠1＝∠2∴∠DAE ＝∠BAC∴A ，B ，D 都可判定△ABC ∽△ADE选项C 中不是夹这两个角的边，所以不相似，故选：C ．【点睛】本题考查了相似三角形的判定：①如果两个三角形的三组对应边的比相等，那么这两个三角形相似；②如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；③如果两个三角形的两个对应角相等，那么这两个三角形相似．9．D解析：D【分析】根据垂直平分线的性质、等腰三角形的性质及判定，相似三角形的判定一一判断即可．【详解】由作图可知，PQ 垂直平分AB ，AB=BD∵PQ 垂直平分AB ，∴AC ＝BC ，∴∠MAN ＝∠CBA ，∵∠MAN ＝30，∴∠DCB ＝∠MAN ＋∠CBA ＝60︒，故选项 A 正确；AB BD =MAN ADB ∴∠=∠∠MAN ＝∠CBA ，ADB CBA ∴∠=∠ACB ABD ∴△∽△2AC ABAB ADAB AC AD ∴=∴=⋅ 故选项B 正确；ABD 为等腰三角形，且两底角均为301803030120ABD ∴∠=︒-︒-︒=︒30MAN CBA ∠=∠=︒4ABD CBA ∴∠=∠故选项C 正确；如图：过点B 作BF AD ⊥在ABF 中，30A ∠=︒3AB AF ∴=22AD AFAB AF =∴=AB AD AD ∴=∴= 故选项D 错误；故选：D ．【点睛】本题考查作图﹣复杂作图，线段的垂直平分线的性质，等腰三角形的性质及判定、相似三角形的判定等知识，解题的关键是熟练掌握基本知识．10．A解析：A【分析】根据平行线分线段成比例定理列出比例式，得到EG ＝3GC ，进而得出结论．【详解】∵DE ∥FG ∥BC ，DF ＝3FB ， ∴EG DF GC FB==3， ∴EG ＝3GC ，∴EC ＝4GC ，故选：A ．【点睛】 本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键． 11．B解析：B【分析】过点F 作//FG AB ，通过证明BED GEF ∽△△可得2FG BD =再证明FCG ACB ∽△△可得AC 的长度，即可求解．【详解】如图，过点F 作//FG AB ，交BC 延长线于点G ，则由平行易知BED GEF ∽△△，因此12BD DE FG EF ==， 即2FG BD =由平行易知FCG ACB ∽△△， 因此FG CF AB AC= ∵3AD BD =，∴4AB AD BD BD =+=， ∴2142FG BD AB BD ==， ∴12CF AC =， 即212AC =， ∴4AC =，∴6AF AC CF =+=．故答案选：B ．【点睛】本题主要考查了利用三角形相似的性质求解线段的长度的问题，正确做出辅助线并证明三角形相似是解决本题的关键．12．D解析：D【分析】已知∠ADC ＝∠BAC ，则A 、B 选项可根据有两组角对应相等的两个三角形相似来判定；C 选项可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定；D 选项虽然也是对应边成比例但无法得到其夹角相等，所以不能推出两三角形相似.【详解】在△ADC 和△BAC 中，∠ADC ＝∠BAC ，如果△ADC ∽△BAC ，需满足的条件有：①∠DAC ＝∠ABC 或AC 是∠BCD 的平分线；②AD DC AB AC=； 故选：D ．【点睛】 此题主要考查了相似三角形的判定方法；熟记三角形相似的判定方法是解决问题的关键．二、填空题13．【分析】由折叠的性质得EF=BE=AE=1CE ⊥BD 设EG=x 可得CG=2x 再根据∆BEG~∆CBG∆BEG~∆CEB 即可求解【详解】解：∵E 为AB 中点∴AE=EB=1∵把沿直线CE对折使点B落在B解析：2【分析】由折叠的性质得EF=BE=AE=1，CE⊥BD，设EG=x，可得CG=2x，再根据∆BEG~∆CBG，∆BEG~∆CEB，即可求解．【详解】AB=，解：∵E为AB中点，2∴AE=EB=1，∆沿直线CE对折，使点B落在BD上的点F处，∵把BCE∴EF=BE=AE=1，CE⊥BD，设CE与BD交于点G，EG=x，∵CD∥AB，∴CG：EG=CD：EB，∴CG=2x，∵BG⊥EC，EB⊥BC，∴∆BEG~∆CBG，∴BG2=CG∙EG∴BG=2x，同理：∆BEG~∆CEB，∴BG：CB=EG：EB，∴BC=AD=2．故答案是：2．【点睛】本题主要考查矩形的性质，相似三角形的判定和性质，熟练掌握“母子相似三角形”模型，是解题的关键．14．44π【分析】证明△OBQ∽△OAP根据相似三角形的性质求出AP根据圆的面积公式计算得到答案【详解】解：如图由题意得OB=08mOQ=OP-PQ=3-1=2（m）BQ∥AP∴△OBQ∽△OAP∴即解解析：44π【分析】证明△OBQ∽△OAP，根据相似三角形的性质求出AP，根据圆的面积公式计算，得到答案．【详解】解：如图，由题意得，OB=0.8m ，OQ=OP-PQ=3-1=2（m ），BQ ∥AP ，∴△OBQ ∽△OAP ， ∴BQ OQ AP OP =，即0.823AP =， 解得，AP=1.2（m ）， 则地面上阴影部分的面积=π×1.22=1.44π（m 2），故答案为：1.44π．【点睛】本题考查的是相似三角形的应用，掌握相似三角形的判定定理和性质定理是解题的关键． 15．6【分析】通过证明△ABC ∽△EFD 可得即可求解【详解】解：∵∠A ＝50°∠B ＝60°∴∠C ＝70°∵∠B ＝∠F ＝60°∠C ＝∠D ∴△ABC ∽△EFD ∴∴∴n ＝6故答案为6【点睛】本题考查了相似三角解析：6【分析】通过证明△ABC ∽△EFD ，可得AB BC EF DF =，即可求解． 【详解】解：∵∠A ＝50°，∠B ＝60°，∴∠C ＝70°，∵∠B ＝∠F ＝60°，∠C ＝∠D ，∴△ABC ∽△EFD ， ∴AB BC EF DF =， ∴392m m n=， ∴n ＝6，故答案为6．【点睛】本题考查了相似三角形的判定和性质，掌握相似三角形的判定定理是本题的关键． 16．【分析】根据L1//L2//L3证明△AOF ∽△EOB ∽△DOC 根据相似三角形的性质即可得到结论【详解】解：∵L1//L2//L3∴∠AFO=∠OCD ∠AOF=∠COD ∴△AOF ∽△DOC 同理△BO 解析：AF CD BE- 【分析】根据L 1//L 2//L 3，证明△AOF ∽△EOB ∽△DOC ，根据相似三角形的性质即可得到结论．【详解】解：∵L 1//L 2//L 3，∴∠AFO=∠OCD ，∠AOF=∠COD∴△AOF ∽△DOC ，同理，△BOE ∽△COD ，△AOF ∽△EOB ， ∴AO AF OE BE =，即AO BE AF OE = ∴OE BE OD CD =， ∴OE BE OE ED CD=+ ∴OE CD BE OE BE ED ⋅=⋅+⋅ ∴()AO AF OE OE CD BE OE AF OE BE ED BE BE BE OE AF C CD BE B D E-=÷=⋅=-- 故答案为：AF CD BE - 【点睛】此题主要考查了相似三角形的判定与性质，熟练掌握相关定理是解答此题的关键． 17．或或【分析】分三种情况讨论当时则则当时由则当时则则再利用相似三角形的性质求解的坐标即可【详解】解：点是线段的中点当时则如图当时由如图当时则综上：或或故答案为：或或【点睛】本题考查的是坐标与图形三角形 解析：(0,3)或(4,0)或70,4⎛⎫ ⎪⎝⎭ 【分析】分三种情况讨论，当PC OA ⊥时，则//,PC OB 则APC AOB ∽，当PC AB ⊥时，由90,,PCB AOB PBC ABO ∠=∠=︒∠=∠ 则BCP BOA △∽△，当CP OB ⊥时，则//,PC OA 则,BCP BAO ∽ 再利用相似三角形的性质求解P 的坐标即可．【详解】解：()()06,8,0,A B ， 点C 是线段AB 的中点，6,8,10,OA OB AB ∴==== 15,2AC AB == 当PC OA ⊥时，则//,PC OB ∴ APC AOB ∽，,AP AC AO AB ∴= 162AP ∴=， ()3,0,3,AP P ∴=如图，当PC AB ⊥时，由90,,PCB AOB PBC ABO ∠=∠=︒∠=∠∴ BCP BOA △∽△，,BC BP BO BA∴= 5,810BP ∴= 25,4BP ∴= 2578,44OP ∴=-=7,0,4P ⎛⎫∴ ⎪⎝⎭如图，当CP OB ⊥时，则//,PC OA,BCP BAO ∴∽,BC BP BA BO∴= 1,28BP ∴= 4,BP ∴=4,OP ∴=()4,0.P ∴综上：()0,3P 或7,04P ⎛⎫ ⎪⎝⎭或()4,0.P 故答案为：()0,3P 或7,04P ⎛⎫⎪⎝⎭或()4,0.P 【点睛】本题考查的是坐标与图形，三角形相似的判定与性质，掌握以上知识是解题的关键． 18．12【分析】首先利用以及平行四边形对边相等分别得到DE 与CEDE 与AB 的比值；再根据平行四边形的性质得出进而推出再根据相似三角形面积比为相似比的平方得出和的面积进而得出四边形的面积即可推出的面积【详 解析：12【分析】首先利用2CD DE =，以及平行四边形对边相等，分别得到DE 与CE 、DE 与AB 的比值；再根据平行四边形的性质得出AB CD ∥，AD BC ∥，进而推出DEF CEB ∽△△，DEF ABF ∽再根据相似三角形面积比为相似比的平方得出CEB △和ABF 的面积，进而得出四边形BCDF 的面积，即可推出ABCD 的面积.【详解】解：∵四边形ABCD 为平行四边形，∴AD BC =，AB CD =，∵2CD DE =，∴3CE DE =，2AB DE =， ∴13DE CE =，12DE AB =， ∵四边形ABCD 为平行四边形，∴AB CD ∥，AD BC ∥，∴DEF CEB ∽△△，DEF ABF ∽， ∴21()9DEF CEB S DE S EC ==△△，21()4DEF ABF S DE S AB ==△△， ∵DEF 的面积为1，∴=9CEB S △，S =4ABF △，∴=S 918BCDF CEB DEF S S -=-=△△，∴=+=8+4=12ABCD BCDF S S S △ABF .故答案为12.【点睛】本题主要考查平行四边形的性质相似三角形的性质和判定，关键在于利用相似三角形的面积比等于相似比的平方.19．296【分析】（1）根据平行四边形的性质得到AE=CE 根据相似三角形的性质得到比例式等量代换得到AF=AD 于是得到2；（2）先得出再利用E 为AO 的中点AO=CO 得出进而得出结果【详解】解：（1）∵在解析：2， 96【分析】（1）根据平行四边形的性质得到AE=13CE ，根据相似三角形的性质得到比例式，等量代换得到AF=13AD ，于是得到FD AF=2； （2）先得出936CEB AEF SS ==，再利用E 为AO 的中点，AO=CO ，得出48ABC S =△，进而得出结果．【详解】 解：（1）∵在▱ABCD 中，AO=12AC ， ∵点E 是OA 的中点， ∴AE=13CE ， ∵AD ∥BC ， ∴△AFE ∽△CBE ， ∴13AF AE BC CE ==，∵AD=BC ，∴AF=13AD ， ∴FD AF=2； （2）由（1）得△AFE ∽△CBE ，且13AE CE =，AEF 的面积为4， ∴936CEB AEF S S == ，∵E 为AO 的中点，AO=CO ，∴1123BAE CEB S S ==，∴48ABC S =△，∴296ABC ABCD S S==四边形 ， 故答案为：2，96．【点睛】本题考查了相似三角形的判定和性质，平行四边形的性质，熟练掌握相似三角形的判定和性质是解题的关键． 20．【分析】先延长EF 和BC 交于点G 再根据条件可以判断三角形ABE 为等腰直角三角形并求得其斜边BE 的长然后根据条件判断三角形BEG 为等腰三角形最后根据△EFD ∽△GFC 得出CG 与DE 的倍数关系并根据BG解析：824+【分析】先延长EF 和BC ，交于点G ，再根据条件可以判断三角形ABE 为等腰直角三角形，并求得其斜边BE 的长，然后根据条件判断三角形BEG 为等腰三角形，最后根据△EFD ∽△GFC 得出CG 与DE 的倍数关系，并根据BG ＝BC ＋CG 进行计算即可．【详解】解：如图，延长EF 和BC ，交于点G ，∵矩形ABCD 中，∠B 的角平分线BE 与AD 交于点E ，∴∠ABE ＝∠AEB ＝45°，∴ AB ＝AE ＝12，∴直角三角形ABE 中，2212122BE +==又∵∠BED 的角平分线EF 与DC 交于点F ，∴∠BEG ＝∠DEF ，∵AD//BC ，∴∠G ＝∠DEF ，∴∠BEG ＝∠G ，∴BG ＝BE ＝，∵∠G ＝∠DEF ，∠EFD ＝∠GFC ，∴△EFD ∽△GFC ， ∴12CG CF DE DF ==， 设CG ＝x ，DE ＝2x ，则AD ＝12＋2x ＝BC ，∵BG ＝BC ＋CG ，∴＝12+2x+x解得：x ＝4，∴ )12244BC=+=，故答案为：4+【点睛】本题主要考查了矩形、相似三角形以及等腰三角形，解决问题的关键是掌握矩形的性质：矩形的四个角都是直角，矩形的对边相等．解题时注意：有两个角对应相等的两个三角形相似． 三、解答题21．（1）证明见解析；（2）CB =【分析】（1）根据三角形外角的性质易证A DBC ∠=∠，再根据∠C 为公共角，即可证明相似； （2）根据相似三角形对应边成比例，即可求得CB 的值．【详解】解：（1）∵ADB A C ∠=∠+∠，ADB DBC C ∠=∠+∠，∴A DBC ∠=∠，∵∠C=∠C ，∴△CBD ∽△CAB ；（2）∵1,2CD AD ==，∴3AC AD DC =+=，∵△CBD ∽△CAB ， ∴CD CB CB AC=，∴13CB CB =，即CB =． 【点睛】 本题考查相似三角形的性质和判定，三角形外角的性质．在证明三角形相似时，不要忽略公共角相等这一条件．22．（1）见解析；（2）见解析．【分析】（1）由三角形的内和定理，角的和差求出∠ADE ＝∠C ，根据两边对应成比例及夹角相等证明△ADF ∽△ACG ，其性质和角平分线的定义得AG 平分∠BAC ；（2）由两对应角相等证明△AEF ∽△ABG ，△ADF ∽△AGC ，其性质得EF AF BG AG =，DF AF CG AG=，再根据等式的性质求出EF•CG ＝DF•B G ． 【详解】（1）证明：180DAE AED ADE ∠+∠+∠=︒，180BAC B C ∠+∠+∠=︒，AED B ∠=∠，ADE C ∴∠=∠，在ADF 和ACG 中， ::AD AC DF CG ADE C=⎧⎨∠=∠⎩ ADF ∴∽ACG ，DAF CAG ∴∠=∠，AG ∴平分BAC ∠；（2）证明：在AEF 和ABG 中，AED B EAF BAG ∠=∠⎧⎨∠=∠⎩， AEF ∴∽ABG ，EF AF BG AG∴=， 在ADF 和AGC 中，DAF CAG ADF C ∠=∠⎧⎨∠=∠⎩， ADF ∴∽AGC ，DF AF CG AG∴=， EF DF BG CG∴=， EF CG DF BG ∴⋅=⋅ ．【点睛】本题综合考查了三角形的内角和定理，相似三角形的判定与性质，角的和差，等量代换，等式的性质等相关知识点，重点掌握相似三角形的判定与性质，难点是利用等式的性质将比例式转换成乘积式．23．（1）23，35；（2）35DM EN =，35BM CN =；（3）4 【分析】（1）在Rt ABC 中，由勾股定理求出10AC ==，由2AD DB =，可得3AB DB =，由//DE BC ，截线段成比例2233AD DE AE DB AB BC AC DB ====，由AD AE AB AC =，分比AB AD AC AE AB AC --=，即BD EC AB AC=即可 （2）由旋转性质可知：AD AM =，AE AN =，BAM CAN =∠∠，由35AB AM AC AN ==，BAM CAN =∠∠，可得ABM ACN △△，由性质35BM AB CN AC ==，ABM ACN ∠=∠，可证DBM ECN △∽△，利用性质35DM BM DB EN CN EC ===； （3）如图4，连接OB ，OE ，由点O 是AC （DF ）的中点，ABC 和DEF 同为等边三角形，可知90BOC DOE ∠=∠=︒，可推得AOD BOE ∠=∠，由::AO BO OD OE ==AOD BOE ∠=∠，可证AOD BOE ∽△△，可得:AD BE =，可求BO =OE =BE BO OE <+，当B 、O 、E 三点共线时（如图5），BE 存在最大值为BE BO OE =+=即可求出．【详解】解：（1）23，35；解答如下：在Rt ABC 中，10AC ==，∵2AD DB =，∴3AB AD DB DB =+=，∵//DE BC ， ∴2233AD DE AE DB AB BC AC DB ====， ∵AD AE AB AC=，∴AB AD AC AE AB AC --=， 即BD EC AB AC =， ∴63105BD AB EC AC ===， 故答案为：23，35； （2）由旋转性质可知：AD AM =，AE AN =，BAM CAN =∠∠， ∵35AB AM AC AN ==，BAM CAN =∠∠， ∴ABM ACN △△， ∴35BM AB CN AC ==，ABM ACN ∠=∠， ∵35BM DB CN EC ==，ABM ACN ∠=∠， ∴DBM ECN △∽△， ∴35DM BM DB EN CN EC ===；（3）BE AD -的最大值为4；提示如下：如图4，连接OB ，OE ，∵点O 是AC （DF ）的中点，ABC 和DEF 同为等边三角形，由三线合一性质可知90BOC DOE ∠=∠=︒，∴BOD COE ∠=∠，∴AOB BOD BOC COE ∠+∠=∠+∠，即AOD BOE ∠=∠，∵::3AO BO OD OE ==，AOD BOE ∠=∠， ∴AOD BOE ∽△△，∴:AD BE =， ∵36AB EF ==， ∴BO =OE =在BOE △中，由三边关系可得，BE BO OE <+，当B 、O 、E 三点共线时（如图5），BE 存在最大值为BE BO OE =+=，∵BE AD BE BE -==，∴当BE 存在最大值时，BE AD -的最大值343=⨯=．【点睛】本题考查三角形全等变换，勾股定理，平行线截比，比例性质，相似三角形的判定与性质，三边关系，线段和差最值，掌握三角形全等的性质，勾股定理，平行线截比，比例性质，相似三角形的判定与性质，三边关系，线段和差最值，解题关键是根据相似求出线段BO 与OE ．24．（1）见解析；（2）∠ACB 的度数为96°或114°；（3）2BC =【分析】（1）由题意可求出1402ACD BCD ACB ∠=∠=∠=°，即证明40ACD A ∠=∠=︒，即△ACD 为等腰三角形．又因为∠CBD =∠ ABC ，可证明△BCD ∽△BAC ，即推出CD 是△ABC 的完美分割线．（2）分情况讨论①当AD =CD 时②当AD =AC 时③当AC =CD 时，根据题意和完美分割线的定义即可求出∠ACB 的大小．（3）根据题意和完美分割线的定义可知，AC =AD =2，△BCD ∽△BAC ，即推出BD CD BC CA=，即可求出BC 长． 【详解】（1）∵40A ∠=︒，60B ∠=︒，∴ 18080ACB A B ∠=︒-∠-∠=︒，∵A B ACB ∠≠∠≠∠，∴ △ABC 不是等腰三角形．∵CD 平分∠ ACB ， ∴1402ACD BCD ACB ∠=∠=∠=°， ∴40ACD A ∠=∠=︒，∴ △ACD 为等腰三角形．∴ 40BCD A ∠=∠=︒，∠CBD =∠ ABC ，∴ △BCD ∽△BAC ，∴ CD 是△ABC 的完美分割线．（2）①如图，当AD =CD 时，∠ACD =∠ A =48°，根据完美分割线的定义，可得△BDC ∽△BCA ，∴∠BCD =∠A =48°，∴∠ACB =∠ACD +∠BCD =96°．②如图，当AD =AC 时，∠ACD =∠ ADC =18048662︒-︒=︒， 根据完美分割线的定义，可得△BDC ∽△BCA ，∴∠BCD =∠A =48°，∴∠ACB =∠ACD +∠BCD =114°．③如图，当AC =CD 时，∠ADC =∠ A =48°．∵△BDC ∽△BCA ，∴∠BCD =∠A =48°，根据完美分割线的定义，可得△BDC ∽△BCA ，∴∠BCD =∠A =48°，∴这与∠ADC >∠BCD 矛盾，所以该情况不符合题意．综上所述，∠ACB 的度数为96°或114°．（3）∵△ACD 是以CD 为底边的等腰三角形，AC =2， ∴AC =AD =2．∵△BCD ∽△BAC ， ∴BD CD BC CA = 3162--=，解得2BC = 【点睛】本题考查等腰三角形判定和性质，相似三角形的判定和性质．根据题意理解完美分割线的定义是解答本题的关键．25．（1）AMN ，证明见解析；（2）34【分析】（1）根据矩形的性质和平行线的性质证明即可；（2）作NH AM ⊥于H ，证明NAH AMB ∆∆∽，根据相似三角形的性质得到212AN BM AM =，根据相似三角形的性质即可得到结论． 【详解】 解：（1）AMN ∆是等腰三角形，证明：四边形ABCD 是矩形，//AD BC ∴，NAM BMA ∴∠=∠，又AMN AMB ∠=∠，AMN NAM ∴∠=∠，AN MN ∴=，即AMN ∆是等腰三角形；（2）如图，延长AD 和ME ，交于点N ，作NH AM ⊥于H ，AN MN =，NH AM ⊥，12AH AM ∴=， 90NHA ABM ∠=∠=︒，AMN AMB ∠=∠，NAH AMB ∴∆∆∽，∴AN AH AM BM=， 212AN BM AH AM AM ∴==， M 为BC 中点，112BM CM BC ∴===， 2223110AM =+=，5AN ，523DN ∴=-=，设DE x =，则3CE x =-，//AN BC ，∴DN DE CM CE =，即313x x=-， 解得，94x =，即94DE =， 34CE ∴=．【点睛】本题考查的是相似三角形的判定和性质、勾股定理的应用以及等腰三角形的性质和矩形的性质，掌握相似三角形的判定定理和性质定理是解题的关键，注意方程思想的正确运用．26．（1）见解析；（2）见解析【分析】（1）利用关于x轴对称点的性质：横坐标相等，纵坐标互为相反数，可以求出1A、1B、C，进而可画出图形；1（2）利用位似图形的性质得出对应点的位置，即可画出图形．【详解】解：(1)如图所示：ΔA1B1C1即为所求；(2)如图所示，ΔA2B2C2即为所求．【点睛】本题考查关于对称轴对称的点的性质以及位似的性质，掌握相关性质是解题的关键．。