下载文档原格式
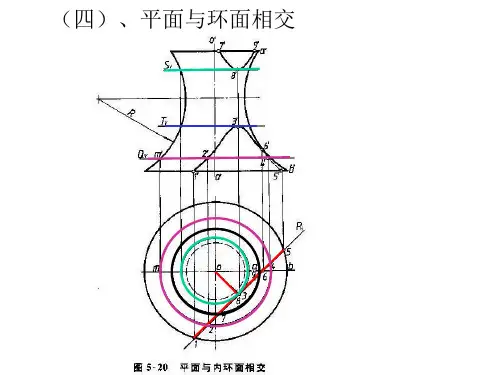
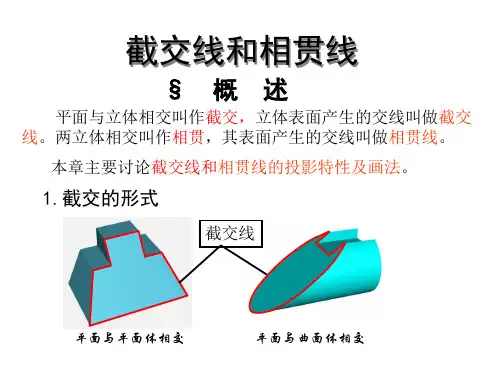
第五讲——相贯线知识点7：相贯线的几何性质及其求法两个相交的立体称为相贯体，其表面的交线称为相贯线。
按照相贯立体的种类，可分为以下三种形式：(1)平面立体与平面立体相贯；(2)平面立体与曲面立体相贯；(3)曲面立体与曲面立体相贯。
由于平面立体的表面均为平面，因而平面立体与平面立体(或曲面立体)相贯，其实质就是平面与平面立体(或曲面立体)相交，也就是“截交”，故只需讨论曲面立体与曲面立体相贯的问题，又因为机械工程中常见的曲面立体就是回转体，因此本节只介绍回转体与回转体相贯时相贯线的求作方法。
相贯线的性质1)两曲面立体的相贯线是两立体表面的共有线或分界线，相贯线上的点是两立体表面上的共有点。
2)由于立体表面是封闭的，因此，相贯线一般为封闭的空间曲线，在特殊情况下，可能是不封闭的，也可能是平面曲线或直线。
3)相贯线的形状取决于曲面的形状、大小及两曲面之间的相对位置。
求作相贯线的方法和步骤根据相贯线的性质，求两回转体相贯线的问题，可归结为求两回转体表面上的共有点的问题。
求作相贯线的一般步骤是：根据给出的投影，分析两相交回转体的形状、大小及其轴线的相对位置，判定相贯线各投影的特点，再进行作图。
求相贯线上点的方法主要有：(1)表面取点法；(2)辅助平面法。
求相贯线时，应首先确定相贯线上的特殊点。
例如，相贯线上与投影面距离最近、最远的点以及位于曲面轮廓线上的点。
因为这些点可以帮助我们确定相贯线投影的大致形状并判别它们的可见性。
除特殊点外，还要作出适当数量的一般点，以便使连线光滑，同时要用虚、实线分别表示不可见和可见的部分。
判别可见性的原则是:只有同时位于两立体可见表面的相贯线投影才是可见的，否则不可见。
知识点7：相贯线的几何性质及其求法。
