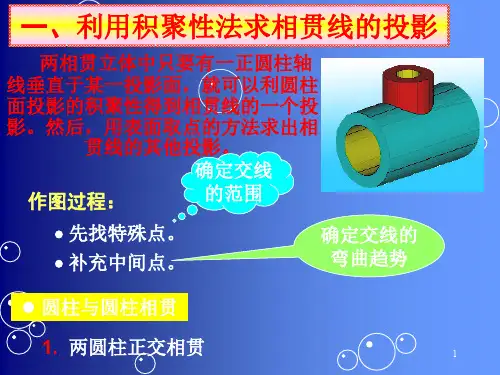
圆柱相贯线画法与识读
- 格式:ppt
- 大小:1.14 MB
- 文档页数:15


一、 新课导入(5分钟)通过上一章节,组合体的组成是将基本基本集合体通过叠加、挖切或者平面相交(截交线)等方式组合在一起。
在组合体零件中会有这样的组合:两个立体相互贯穿,产生相贯线【分析】:相贯线是由两个立体相互贯穿而产生的,那么,在我们生活当中以哪些物体上会出现相贯线?它的形状是怎样的?【引导】:引导学生得到结论:★各种阀体、管件的三通、四通、各种栏杆、健身器材等,这些物体表面上都会有相贯线的存在。
★相贯线为一条封闭的空间曲线。
二、 讲授新课(32分钟) 1. 相贯线的概念和性质导入新课。
先同析注意:不准确的地方,不直接否定,通过其他同学的补充发言予以充实和纠正。
启发、引导侧两个几何体相交,其表面交线称为相贯线。
相贯线的性质:(1)相贯线是两相交立体表面共有点的集合,也是两相交立体表面的分界线; (2)一般情况下,相贯线是封闭的空间曲线,特殊时是平面曲线或直线。
2. 不同直径两圆柱正交相贯的画法求相贯线的实质即是求它们表面的共有点,然后依次光滑地连接即为相贯线。
方法:积聚性和表面取点法。
作图方法(1)求特殊点;(2)求一般点;(3)顺次光滑连接各点,即得相贯线的正面投影。
注意:示整个画图过程。
在中,讲解第二、三步内容。
增加课堂练习,加强学生的动手能力。
在课堂练习的同时,请同学们认真问题,并把该问题做为下节课的提问。
让因,然后学们找到答案。
阐明优缺点:画相贯线时取的点在其余两个视图上的位置比较精确,但是,因为是手工连接各点,使得相贯线不光滑、美观。
【任务一】:绘制圆柱正交相贯,按照刚教给同学们的方法学生自己做一下。
【巡视】:看学生们掌握得如何,在巡视的过程中加以指导。
【思考】:(约2分钟)如果两相贯的圆柱直径都较大时,我们该怎么办? 在特殊点的基础上再取四个点。
3、简化画法:国家标准规定,允许采用简化画法作出相贯线的投影,即以圆弧代替非圆曲线。
注:仅限两圆柱直径相差较大,且正交情况阐明优缺点:相贯线非常光滑、美观,但是,相贯线的形状为近似画出。




圆柱与圆柱相贯
1.表面取点法求作相贯线
两圆柱正交,且圆柱轴线为投影面垂直线时,在该投影面上,圆柱面投影是有积聚性的,相贯线在该投影面上的投影,就落在圆柱面有积聚性的投影上。
因此,可以在首先确定出相贯线的两面投影,在这些相贯线的已知投影上取一些点,再利用投影关系求作出相贯线的第三面投影上相应的点,这就是表面取点法。
例1:如图4-15所示,求作两正交圆柱的相贯线。
解:由图4-15b 可见,大、小圆柱的轴线分别垂直于侧立投影面和水平投影面,大圆柱的侧面投影积聚为圆,小圆柱的水平投影积聚为圆。
那么相贯线的侧面投影为圆弧(与大圆柱的部分积聚投影重合),相贯线的水平投影为圆(与小圆柱的水平积聚投影重合)。
相贯线的正面投影,可用已知点、线的两个投影求另外一个投影的方法来求得。
作图步骤如下(如图4-14c 所示):
a) 立体图 b) 原题 c) 作图步骤
图4-15 圆柱与圆柱正交 l )先求特殊点,即求相贯线上的最前、最后、最左、最右、最上、最下等点。
在水平投影的小圆周上直接确定出相贯线上最左、最右点的投影1、3和最前、最后点的投影2、4;对应在侧面投影中为1”、(3”)和2”、4”,也是相贯线上的最高、最低点的侧面投影;按投影关系可得出它们的正面投影1’、3’和2’、(4’)。
因为相贯两圆柱体前后对称,故最前、最后两点的正面投影重合。
2)求作一般位置点。
依连线光滑准确的需要,作出相贯线上若干个中间点的投影。
如在水平投影上取5、6点,其侧面投影为5”、6”,再求出其正面投影5’和6’。
3)依次光滑连接l’、5’、2’(4’)、6’、3’各点,即得相贯线的正面投影。

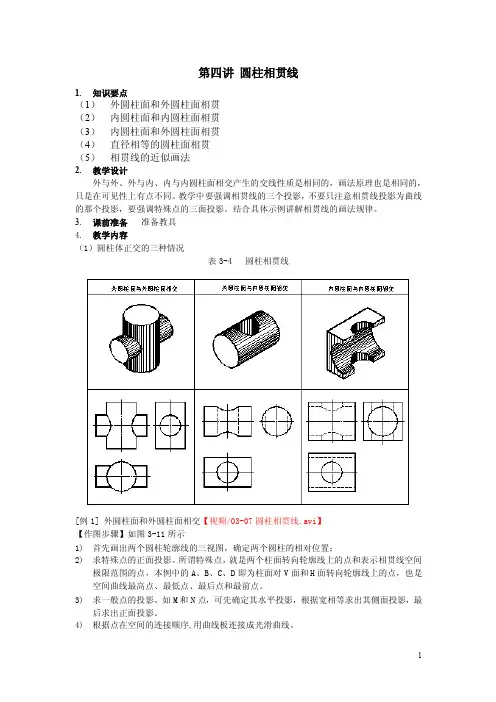
第四讲圆柱相贯线1.知识要点(1)外圆柱面和外圆柱面相贯(2)内圆柱面和内圆柱面相贯(3)内圆柱面和外圆柱面相贯(4)直径相等的圆柱面相贯(5)相贯线的近似画法2.教学设计外与外、外与内、内与内圆柱面相交产生的交线性质是相同的,画法原理也是相同的,只是在可见性上有点不同。
教学中要强调相贯线的三个投影,不要只注意相贯线投影为曲线的那个投影,要强调特殊点的三面投影。
结合具体示例讲解相贯线的画法规律。
3.课前准备准备教具4.教学内容(1)圆柱体正交的三种情况表3-4 圆柱相贯线[例1] 外圆柱面和外圆柱面相交【视频/03-07圆柱相贯线.avi】【作图步骤】如图3-11所示1)首先画出两个圆柱轮廓线的三视图,确定两个圆柱的相对位置;2)求特殊点的正面投影。
所谓特殊点,就是两个柱面转向轮廓线上的点和表示相贯线空间极限范围的点,本例中的A、B、C、D即为柱面对V面和H面转向轮廓线上的点,也是空间曲线最高点、最低点、最后点和最前点。
3)求一般点的投影。
如M和N点,可先确定其水平投影,根据宽相等求出其侧面投影,最后求出正面投影。
4)根据点在空间的连接顺序,用曲线板连接成光滑曲线。
图3-11 圆柱相贯线画法[例2] 直径相等的两个外圆柱面相交【Flash动画/03-10圆柱相贯线.swf】上例中假想大圆柱的直径不变,而小圆柱的直径变大,D点的V面投影将向右移动,A 点V面投影将向上移动。
当两个圆柱的直径相等时,相贯线将由空间曲线变为平面曲线椭圆,若竖直放置的圆柱面只有左半个柱面参与相贯,则相贯线的空间形状为两段椭圆弧,且椭圆平面和V面处于垂直位置,所以,相贯线的V面投影为两段直线。
【分析】若两个直径相等的柱面互相贯穿,则相贯线为两个完整的椭圆,两个椭圆在柱面不反映圆的视图上,聚积成直线。
如图3-12所示。
图3-12 直径相等的两个柱面相交【视频/03-08等直径圆柱相交.avi】[例3] 外圆柱面和内圆柱面相交【视频/03-09内、外圆柱面相交.avi】【分析】外圆柱面和内圆柱面相交、内圆柱面和内圆柱面相交时,相贯线的形状和外圆柱面与外圆柱面相交时相贯线的形状相同,画法也完全一样。
相同直径圆柱的相贯线
相贯线是两个立体相交时,它们的交线在其中一个立体上的投影。
当两个相同直径的圆柱相交时,它们的相贯线是一个椭圆。
为了找到这个椭圆,我们可以使用以下步骤:
1.确定相贯线的中心:相贯线的中心是两个圆柱的中心连线的中点。
2.确定相贯线的长轴和短轴:
o长轴:等于两个圆柱的中心距离。
o短轴:等于圆柱的直径。
3.确定椭圆的方程:
假设圆柱的半径为r,两个圆柱的中心距离为2c,则相贯线的椭圆方程为:
c2x2+r2y2=1
其中,x是从相贯线中心到椭圆上任一点的水平距离,y是从相贯线中心到椭圆上任一点
的垂直距离。
4.绘制相贯线:使用上述椭圆方程,在适当的坐标系中绘制椭圆。
请注意,这只是一个基本的描述。
在实际应用中,可能还需要考虑其他因素,如圆柱的倾斜角度、相对位置等。
此外,绘制相贯线时,可能需要使用专业的CAD软件或其他绘图工具。