【解析】陕西省西工大附中2014届高三上学期第一次适应性训练数学(文)试题

2013年普通高等学校招生全国统一考试西工大附中适应性训练高三数学（文科）本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分。

考试时间120分钟第Ⅰ卷（选择题 共50分）一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知集合(){}(){2,1,,A x y y x B x y y ==-==，则A B I 的真子集个数为（ ）A ． 3B ． 6C ． 7D ．8 【答案】C【解析】2221111=1,11x x x y x x x ⎧-><-⎪=-⎨--<<⎪⎩，或，221(0)x y y +=≥，画出图像，与图像知：它们共有3个交点，所以A B I 的真子集个数为3217-=。

2．若两个非零向量,a b r r 满足2a b a b a +=-=r r r r r ，则向量a b +r r 与a b -r r 的夹角为（ ）A ．6π B ． 4πC ． 23πD ．56π【答案】C【解析】因为2a b a b a +=-=r r r r r，所以以OA 、OB 为邻边做的平行四边形为矩形，所以,66OBA COB ππ∠=∠=，23ODB π∠=，所以向量a b +r r 与a b -r r 的夹角为23π。

3．下面四个条件中，使a b >成立的充分不必要条件是（ ） A ．1a b >+ B ．1a b >- C ． 22a b > D ．33a b >【答案】A【解析】A ．若1a b >+，则a b >一定成立；但若a b >，不一定1a b >+，因此“1a b >+”是 “a b >”的一个充分不必要条件；B ．若1a b >-，则a b >不一定成立，不是充分条件；C ．若22a b >，则a b >不一定成立，不是充分条件；D ．若33a b >，则a b >一定成立；若a b >，则33a b >也一定成立，因此“33a b >”是 “a b >”的一个充要条件。

西工大附中2014届高三上学期第一次适应性训练理综试题可能用到的相对原子质量：H-1、C-12、O-16、N-14、S-32、Fe-56、Cr-52、Hg-201第Ⅰ卷（选择题共126分）一、选择题：本题共13小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一个选项最符合题目要求。

1. 下列有关细胞物质组成的叙述，正确的是A．叶绿体、线粒体和核糖体都含有DNAB．糖类不参与细胞识别和免疫调节C．胆固醇是构成动物细胞膜的重要成分D．N是A TP、核糖核酸、脂肪等多种化合物的组成元素2. 研究表明硒对线粒体膜有稳定作用,可以推测人体缺硒时下列细胞中最易受损的是A．脂肪细胞B．心肌细胞C．口腔上皮细胞D．淋巴细胞3. 下列有关生物实验的描述，正确的是A. 观察洋葱根尖细胞分裂图像，处于分裂前期的细胞可观察到四分体B. 在探究pH对酶活性的影响实验中，pH是自变量，温度是无关变量C. 检测酵母菌培养过程是否产生CO2可判断其呼吸方式D. 成熟植物细胞在高渗溶液中发生质壁分离是因为细胞壁具有选择透过性4. 小华不小心碰到滚烫的开水壶，手会迅速缩回。

关于该反射的叙述，正确的是A. 反射活动中需要神经递质参与兴奋的传递B. 突触后膜上会发生“电信号——化学信号——电信号”的转变过程C. 神经冲动在神经纤维上单向传导，在突触处双向传递D. 刺激以电信号的形式在整个反射弧中进行传导5. 下图为甲种遗传病（基因为A、a）和乙种遗传病（基因为B、b）的家系图。

其中一种遗传病基因位于常染色体上，另一种位于X染色体上。

调查结果显示，正常女性人群中甲、乙两种遗传病基因携带者的概率分别为1/10000和1/100，下列说法正确的是A. 调查上述两种遗传病的发病率时，最好选择在患者家系中调查B. 甲种遗传病的遗传方式为伴X染色体隐性遗传，乙种遗传病的遗传方式为常染色体隐性遗传C．据图分析，Ⅲ-3的甲种遗传病的致病基因来源于Ⅰ-1和Ⅰ-2，乙种遗传病的致病基因来源于Ⅰ-4D ．H 如果是男孩则表现甲、乙两种遗传病的概率分别是1/60000和1/2006. 棉蚜体型微小，能附着于棉花植株上生活繁殖，以吸收棉花汁液为食。

2014届普通高等学校招生全国统一考试西工大附中第一次适应性训练语文本试卷分第I卷(阅读题)和第Ⅱ卷(表达题)两部分。

考生作答时，将答案答在答题卡上(答题注意事项见答题卡)，在本试题卷上答题无效。

考试结束后，将答题卡交回。

第Ⅰ卷阅读题甲必考题（共45分）一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1～3题。

圆是中国文化中的一个重要精神原型，它与中国人的宇宙意识、生命情调等有十分密切的关系，也是我们揭示中国艺术生命秘密的不可忽视的因素。

人有悲欢离合，月有阴晴圆缺，圆有时是相对于缺而言的。

我们通常所说的“圆满”一语，原是中国哲学的一个重要概念，其中也可看出中国人重视艺术生命的一份用心。

司空图《诗品〃雄浑》“超以象外，得其环中”云：“超以象外，至大不可限制；得其环中，理之圆足混成无缺，如太极然。

”在这里，圆即充满、周备、具足，体现在诗性艺心就是浑全充融。

森罗万象，一尘沤，一片叶，一缕云，及至浩浩苍天、绵绵大地，都可以大道涵括。

中国哲学中有一个著名比喻：“月印万川”，最能体现充满圆融的特点。

这个比喻有两层重要的含义：一是万川之月，只是一月。

江流宛转绕芳甸，何处春江无月明，湛然寰宇，月光朗照，天下万千江湖，无处不映出它的圆影。

然万千个圆共有一圆，万种之月，只有一月相照，一圆贯穿了万川之圆，散在江湖各处的异在之圆联成一个整体，只有一个生命。

二是自此一月，可观全月。

由于散在江湖的万千之月均由一月相照，故自任何一月均可窥见万千之月的内在生命，任何江湖的月都是一个自我完足的生命世界。

“万川之月”所透析出的哲学内蕴就是：一即一切，一切即一，它强调了万物都是一个自在圆足的生命这一重要特性。

中国哲学的圆满具足说散发着浓厚的艺术情调，它实际上是以审美的眼光看待世界。

儒道佛中的充满圆融的生命哲学刺激了中国艺术家的创造精神。

由于受天人合一哲学观念的影响，中国艺术家总有一种自觉的超越意识，要尽广大，极精微，自有限而观无限，由当下而观永恒。

（陕西江西版第03期） 2014届高三数学试题分省分项汇编专题13 推理与证明、新定义文（含解析）一．基础题组1. 【陕西工大附中第一次适应性训练】将全体正整数排成一个三角形数阵：按照以上排列的规律，第n行（n≥3）从左向右的第3个数为．2. 【陕西工大附中第一次适应性训练】定义运算a b⊗为执行如图所示的程序框图输出的s值，则552cos2tan34ππ⎛⎫⎛⎫⊗⎪ ⎪⎝⎭⎝⎭的值为（）A．4 B．3 C．2 D．―13. 【江西省七校2014届高三上学期第一次联考】定义行列式运算12122112a a ab a b b b =-，将函数sin 2()cos 2xf x x=的图象向左平移t （0t >）个单位，所得图象对应的函数为奇函数，则t 的最小值为 （ ） A ．6πB ．3πC ．56πD ．23π二．能力题组1. 【江西省稳派名校学术联盟2014届高三12月调研考试】将2n按如表的规律填在5列的数表中，设20142排在数表的第n 行，第m 列，则m ＋n ＝___________。

12 22 32 428272 62 5292 102 112 122162152142132……………【答案】507 【解析】试题分析：由于2014＝4×503＋2，故22014在第504行第3列，m ＋n ＝507考点：归纳推理． 【结束】 三．拔高题组1. 【陕西省咸阳市范公中学2014届高三上学期摸底考试】已知数列{a n }的通项为*(1)log (2)()n n a n n N +=+∈，我们把使乘积123n a a a a 为整数的n 叫做“优数”，则在(12012]，内最大的“优数”为（ ）． A ．510 B ．512 C ．1022 D ．10242. 【江西宜春市二高2014届高三第五次数学（文科）月考试卷】若数列{}n A 满足21n n A A =+，则称数列{}n A 为“平方递推数列”．已知数列{}n a 中，91=a ，点),(1+n n a a 在函数x x x f 2)(2+=的图象上，其中n 为正整数．(Ⅰ)证明数列{1}n a +是“平方递推数列”，且数列{lg(1)}n a +为等比数列； (Ⅱ）设（Ⅰ)中“平方递推数列”的前n 项积为n T ，即12(1)(1)(1)n n T a a a =+++，求lg n T ；(Ⅲ）在(Ⅱ）的条件下，记)1lg(lg +=n nn a T b ，求数列{}n b 的前n 项和n S ，并求使2014n S >的n 的最小值．。

【解析】陕西省西工大附中2014届高三上学期第四次适应性训练数学（文）试题1．复数151i（i 为虚数单位）的值为（）A.iB. 1C.i D.1【答案】A 【解析】153111i iii.2．已知,01|2xx A1,0,1,2B ，则()R C A B（）A.2,1B.2C.1,0,1 D.0,1【答案】C 【解析】因为2|10|11,Ax xx x x或1,0,1,2B ，所以()R C A B1,0,1.3．1x是2320xx的（）条件A.充分不必要 B. 必要不充分 C.充要 D.既不充分又不必要【答案】A【解析】因为方程2320x x 的根为1和2，所以1x 是2320xx 的充分不必要条件。

4．将函数sin()3yx的图象上所有点的横坐标伸长到原的2倍（纵坐标不变），再将所得的图象向左平移3个单位，得到的图象对应的解析式是（）A. 1sin2y x B.1sin()22y xC. 1sin()26yxD.sin(2)6yx【答案】C 【解析】将函数sin()3yx的图象上所有点的横坐标伸长到原的2倍（纵坐标不变），得到函数1sin()23yx的图像，再将所得的图象向左平移3个单位，得到的图象对应的解析式是11sin sin()23326yxx。

5. 某几何体的主视图与左视图都是边长为1的正方形，且体积为12，则该几何。

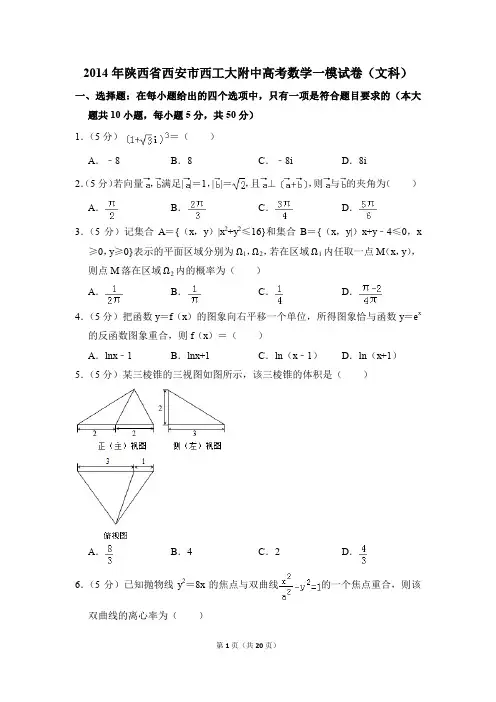
2014年陕西省西安市西工大附中高考数学一模试卷（文科）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（本大题共10小题，每小题5分，共50分）1．（5分）＝（）A．﹣8B．8C．﹣8i D．8i2．（5分）若向量，满足||＝1，||＝，且⊥，则与的夹角为（）A．B．C．D．3．（5分）记集合A＝{（x，y）|x2+y2≤16}和集合B＝{（x，y|）x+y﹣4≤0，x ≥0，y≥0}表示的平面区域分别为Ω1，Ω2，若在区域Ω1内任取一点M（x，y），则点M落在区域Ω2内的概率为（）A．B．C．D．4．（5分）把函数y＝f（x）的图象向右平移一个单位，所得图象恰与函数y＝e x 的反函数图象重合，则f（x）＝（）A．lnx﹣1B．lnx+1C．ln（x﹣1）D．ln（x+1）5．（5分）某三棱锥的三视图如图所示，该三棱锥的体积是（）A．B．4C．2D．6．（5分）已知抛物线y2＝8x的焦点与双曲线的一个焦点重合，则该双曲线的离心率为（）A．B．C．D．37．（5分）有五瓶墨水，其中红色一瓶，蓝色、黑色各两瓶，某同学从中随机任取出两瓶，若取出的两瓶中有一瓶是蓝色，求另一瓶也是蓝色的概率（）A．B．C．D．8．（5分）已知等差数列{a n}中，S n为其前n项和，若a1＝﹣3，S5＝S10，则当S n取到最小值时n的值为（）A．5B．7C．8D．7或89．（5分）定义运算a⊗b为执行如图所示的程序框图输出的S值，则的值为（）A．4B．3C．2D．﹣110．（5分）如图是1，2两组各7名同学体重（单位：kg）数据的茎叶图．设1，2两组数据的平均数依次为和，标准差依次为s 1和s2，那么（）（注：标准差，其中为x1，x2，…，x n 的平均数）＞s2B．，s1＜s2A．，sC．，s 1＜s2D．，s1＞s2二．填空题：把答案填在答题卡相应题号后的横线上（本大题共4小题，每小题5分，共25分）11．（5分）已知函数则满足不等式f（f（x））＞1的x的取值范围是．12．（5分）将全体正整数排成一个三角形数阵：按照以上排列的规律，第n行（n≥3）从左向右的第3个数为．13．（5分）在△ABC中，，，，则B＝．14．（5分）若直线y＝kx+1被圆x2+y2﹣2x﹣3＝0截得的弦最短，则实数k的值是．三、选做题（请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）（共3小题，满分5分）15．（5分）（极坐标与参数方程选讲选做题）极坐标系下曲线ρ＝4sinθ表示圆，则点到圆心的距离为．16．已知P A是圆O的切线，切点为A，P A＝2．AC是圆O的直径，PC与圆O 交于点B，PB＝1，则圆O的半径R＝．17．（不等式选讲选做题）若关于x的不等式存在实数解，则实数a的取取值范围是．三．解答题：解答应写出文字说明、证明过程或演算步骤（本大题共6小题，共75分）18．（12分）已知在等比数列{a n}中，a1＝1，且a2是a1和a3﹣1的等差中项．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若数列{b n}满足b n＝2n﹣1+a n（n∈N*），求{b n}的前n项和S n．19．（12分）在△ABC中，角A、B、C所对应的边分别为a、b、c．（1）叙述并证明正弦定理（2）设，求sin B的值．20．（12分）某校有教职工130人，对他们进行年龄状况和受教育情况（只有本科和研究生两类）的调查，其结果如下：（1）随机抽取一人，是35岁以下的概率为，求a，b的值；（2）从50岁以上的6人中随机抽取两人，求恰好只有一位研究生的概率．21．（12分）如图，在四棱锥S﹣ABC中，底面ABCD是矩形，SA⊥底面ABCD，SA＝AD，点M是SD的中点，AN⊥SC，且交SC于点N．（Ⅰ）求证：SB∥平面ACM；（Ⅱ）求证：平面SAC⊥平面AMN．22．（13分）已知椭圆C的中心在坐标原点，短轴长为4，且有一个焦点与抛物线的焦点重合．（1）求椭圆C的方程．（2）已知经过定点M（2，0）且斜率不为0的直线l交椭圆C于A、B两点，试问在x轴上是否另存在一个定点P使得PM始终平分∠APB？若存在求出P点坐标，若不存在请说明理由．23．（14分）已知函数f（x）＝lnx，g（x）＝ax2+2x（1）若曲线y＝f（x）﹣g（x）在x＝1与x＝处的切线相互平行，求a的值及切线斜率．（2）若函数y＝f（x）﹣g（x）在区间（，1）上单调递减，求a的取值范围．（3）设函数f（x）的图象C1与函数g（x）的图象C2交与P、Q两点，过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N，证明：C1在点M处的切线与C2在点N处的切线不可能平行．2014年陕西省西安市西工大附中高考数学一模试卷（文科）参考答案与试题解析一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（本大题共10小题，每小题5分，共50分）1．（5分）＝（）A．﹣8B．8C．﹣8i D．8i【解答】解：故选：A．2．（5分）若向量，满足||＝1，||＝，且⊥，则与的夹角为（）A．B．C．D．【解答】解：由题意可得＝0，即＝0，∴1+1××cos＜＞＝0．解得cos＜＞＝﹣．再由＜＞∈[0，π]，可得＜＞＝，故选：C．3．（5分）记集合A＝{（x，y）|x2+y2≤16}和集合B＝{（x，y|）x+y﹣4≤0，x ≥0，y≥0}表示的平面区域分别为Ω1，Ω2，若在区域Ω1内任取一点M（x，y），则点M落在区域Ω2内的概率为（）A．B．C．D．【解答】解：根据题意可得集合A＝{（x，y）|x2+y2≤16}所表示的区域即为如图所表示的圆及内部的平面区域，面积为16π，集合B＝{（x，y）|x+y﹣4≤0，x≥0，y≥0}表示的平面区域即为图中的Rt△AOB，S△AOB＝×4×4＝8，根据几何概率的计算公式可得P＝＝，故选：A．4．（5分）把函数y＝f（x）的图象向右平移一个单位，所得图象恰与函数y＝e x 的反函数图象重合，则f（x）＝（）A．lnx﹣1B．lnx+1C．ln（x﹣1）D．ln（x+1）【解答】解：由函数y＝e x可得x＝lny，故函数的反函数为y＝lnx，由题意可得，把y＝lnx的图象向左平移一个单位，可得f（x）＝ln（x+1）的图象，故选：D．5．（5分）某三棱锥的三视图如图所示，该三棱锥的体积是（）A．B．4C．2D．【解答】解：由三视图可知：该三棱锥的侧面PBC⊥底面ABC，PD⊥交线BC，AE⊥BC，且AE＝3，PD＝2，CD＝3，DB＝1，CE＝EB＝2．＝＝＝4．∴V P﹣ABC故选：B．6．（5分）已知抛物线y2＝8x的焦点与双曲线的一个焦点重合，则该双曲线的离心率为（）A．B．C．D．3【解答】解：∵抛物线y2＝8x的焦点是（2，0），∴c＝2，a2＝4﹣1＝3，∴e＝．故选：B．7．（5分）有五瓶墨水，其中红色一瓶，蓝色、黑色各两瓶，某同学从中随机任取出两瓶，若取出的两瓶中有一瓶是蓝色，求另一瓶也是蓝色的概率（）A．B．C．D．【解答】解：设“取出的两瓶中有一瓶是蓝色”为事件A，“另一瓶也是蓝色”为事件B，这时，事件A所包含的基本事件n（A）＝+•＝7 （个），而AB同时发生所包含的事件个数n（AB）＝＝1，故取出的另一瓶也是蓝色的概率为P（B/A）＝＝，故选：B．8．（5分）已知等差数列{a n}中，S n为其前n项和，若a1＝﹣3，S5＝S10，则当S n取到最小值时n的值为（）A．5B．7C．8D．7或8【解答】解：设等差数列{a n}的公差为d，∵a1＝﹣3，S5＝S10，∴＝10×（﹣3）+，解得d＝．∴＝，令a n≥0，解得n≥8．因此前7，8项的和取得最小值．故选：D．9．（5分）定义运算a⊗b为执行如图所示的程序框图输出的S值，则的值为（）A．4B．3C．2D．﹣1【解答】解：由已知的程序框图可知：本程序的功能是：计算并输出分段函数S＝的值∵a＝＝1，b＝＝2∴S＝2×（1+1）＝4故选：A．10．（5分）如图是1，2两组各7名同学体重（单位：kg）数据的茎叶图．设1，2两组数据的平均数依次为和，标准差依次为s 1和s2，那么（）（注：标准差，其中为x1，x2，…，x n 的平均数）A．，s＞s2B．，s1＜s2C．，s 1＜s2D．，s1＞s2【解答】解：由茎叶图，得第1组的7名同学的体重分别为53 56 57 58 6170 72，∴第1组的7名同学体重的平均数为：＝（53+56+57+58+61+70+72）＝61kg 因此，第1组的7名同学体重的方差为：s2＝[（53﹣61）2+（56﹣61）2+…+（72﹣61）2]＝43.00kg2，同理，第2组的7名同学体重的平均数为：＝（54+56+58+60+61+72+73）＝62kg因此，第2组的7名同学体重的方差为：s2＝[（54﹣62）2+（56﹣62）2+…+（73﹣62）2]＝63.14kg2，∴且s 1＜s2故选：C．二．填空题：把答案填在答题卡相应题号后的横线上（本大题共4小题，每小题5分，共25分）11．（5分）已知函数则满足不等式f（f（x））＞1的x的取值范围是（4，+∞）．【解答】解：由题意，x≤0时f（x）在（0，1]之间，x＞0时f（x）值域为R 因为f（f（x））＞1，如果取T＝f（x），则T应该大于零，所以f（T）＝log2T＞1，则必有T＞2∴f（x）＞2＞1∴f（x）＝log2x＞2∴x＞4∴x的取值范围是（4，+∞）故答案为：（4，+∞）12．（5分）将全体正整数排成一个三角形数阵：按照以上排列的规律，第n行（n≥3）从左向右的第3个数为．【解答】解：本小题考查归纳推理和等差数列求和公式．前n﹣1行共有正整数1+2+…+（n﹣1）个，即个，因此第n行第3个数是全体正整数中第+3个，即为．另解：最左边的数a1＝1，a2＝2，a3＝4，a4＝7，a5＝11，…，a2一a1＝1，a3一a2＝2，a4一a3＝3，a5一a4＝4，＝n一1，…a n一a n﹣1累加得a n一a1＝1十2十3十4十…十（n一1）＝（1十n一1）（n一1），即a n＝1十n（n一1），则所求数为．13．（5分）在△ABC中，，，，则B＝．【解答】解：在△ABC中，，，，则由大边对大角可得B＜A，故B＜．再由正弦定理可得＝，解得sin B＝，故B＝，故答案为．14．（5分）若直线y＝kx+1被圆x2+y2﹣2x﹣3＝0截得的弦最短，则实数k的值是1．【解答】解：直线y＝kx+1过定点M（0，1），圆x2+y2﹣2x﹣3＝0的圆心为（1，0），半径为r＝2，显然点M在圆内若直线y＝kx+1被圆x2+y2﹣2x﹣3＝0截得的弦最短，则圆心（1，0）与点M（0，1）的连线与直线y＝kx+1垂直，即k×＝﹣1，故k＝1故答案为1三、选做题（请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）（共3小题，满分5分）15．（5分）（极坐标与参数方程选讲选做题）极坐标系下曲线ρ＝4sinθ表示圆，则点到圆心的距离为．【解答】解：由曲线ρ＝4sinθ化为ρ2＝4ρsinθ，∴x2+y2＝4y，化为x2+（y﹣2）2＝4，可得圆心C（0，2）．由点，可得＝2，y A＝＝2，∴A．∴|AC|＝＝．故答案为：．16．已知P A是圆O的切线，切点为A，P A＝2．AC是圆O的直径，PC与圆O交于点B，PB＝1，则圆O的半径R＝．【解答】解：依题意，我们知道△PBA～△ABC，由相似三角形的对应边成比例性质我们有，即．故答案为：．17．（不等式选讲选做题）若关于x的不等式存在实数解，则实数a的取取值范围是（﹣∞，0）∪．【解答】解：令f（x）＝|x+1|﹣|x﹣2|，则f（x）＝，如图所示．∵关于x的不等式存在实数解，∴＜f（x）max＝3，解得，故a的取值范围是（﹣∞，0）∪．故答案为（﹣∞，0）∪．三．解答题：解答应写出文字说明、证明过程或演算步骤（本大题共6小题，共75分）18．（12分）已知在等比数列{a n}中，a1＝1，且a2是a1和a3﹣1的等差中项．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若数列{b n}满足b n＝2n﹣1+a n（n∈N*），求{b n}的前n项和S n．【解答】解：（I）设等比数列{a n}的公比为q，∵a2是a1和a3﹣1的等差中项，a1＝1，∴2a2＝a1+（a3﹣1）＝a3，∴＝2，∴＝2n﹣1，（n∈N*）．（Ⅱ）∵b n＝2n﹣1+a n，∴（2n﹣1+2n﹣1）＝[1+3+5+…+（2n﹣1）]+（1+2+22+…+2n﹣1）＝+＝n2+2n﹣1．19．（12分）在△ABC中，角A、B、C所对应的边分别为a、b、c．（1）叙述并证明正弦定理（2）设，求sin B的值．【解答】解：（1）正弦定理：在一个三角形中，各边和它所对角的正弦的比相等．即＝＝（2R三角形外接圆的直径），证明：在△ABC中，设BC＝a，AC＝b，AB＝c．作CH⊥AB垂足为点H，可得：CH＝a•sin B，CH＝b•sin A，∴a•sin B＝b•sin A，得到＝同理，在△ABC中，＝，∵同弧所对的圆周角相等，∴＝2R，则＝＝（2R三角形外接圆的直径）；（2）在△ABC中，∵a+c＝2b，由正弦定理可得sin A+sin C＝2sin B，∴2sin cos＝4sin cos，再由A﹣C＝，可得sin cos＝2sin cos，解得：sin＝，∴cos＝，则sin B＝2sin cos＝．20．（12分）某校有教职工130人，对他们进行年龄状况和受教育情况（只有本科和研究生两类）的调查，其结果如下：（1）随机抽取一人，是35岁以下的概率为，求a，b的值；（2）从50岁以上的6人中随机抽取两人，求恰好只有一位研究生的概率．【解答】解：（1）由已知得：，解得a＝50…（3分）故b＝130﹣（50+35+25+4+2）＝14，即b＝14．…（6分）（2）将50岁以上的6人进行编号：四位本科生为：1，2，3，4，两位研究生为5，6．从这6人中任取2人共有15种等可能发生的基本事件，分别为：12，13，14，15，16，23，24，25，26，34，35，36，45，46，56，共有15种抽法，…（9分）其中恰好有一位研究生的有8种，分别为：15，16，25，26，35，36，45，46，共有8种抽法，故所求的事件概率为：．…（12分）21．（12分）如图，在四棱锥S﹣ABC中，底面ABCD是矩形，SA⊥底面ABCD，SA＝AD，点M是SD的中点，AN⊥SC，且交SC于点N．（Ⅰ）求证：SB∥平面ACM；（Ⅱ）求证：平面SAC⊥平面AMN．【解答】证明：（Ⅰ）连接BD，交AC于点O，连接MO ∵ABCD为矩形，∴O为BD中点又M为SD中点，∴MO∥SB…（3分）MO⊂平面ACM，SB⊄平面AC…（4分）∴SB∥平面ACM…（5分）（Ⅱ）∵SA⊥平面ABCD，∴SA⊥CD∵ABCD为矩形，∴CD⊥AD，且SA∩AD＝A，∴CD⊥平面SAD，∴CD⊥AM…（8分）∵SA＝AD，M为SD的中点，∴AM⊥SD，且CD∩SD＝D，∴AM⊥平面SCD，∴AM⊥SC…（10分）又∵SC⊥AN，且AN∩AM＝A，∴SC⊥平面AMN．∵SC⊂平面SAC，∴平面SAC⊥平面AMN．…（12分）22．（13分）已知椭圆C的中心在坐标原点，短轴长为4，且有一个焦点与抛物线的焦点重合．（1）求椭圆C的方程．（2）已知经过定点M（2，0）且斜率不为0的直线l交椭圆C于A、B两点，试问在x轴上是否另存在一个定点P使得PM始终平分∠APB？若存在求出P 点坐标，若不存在请说明理由．【解答】解：（1）设椭圆的标准方程为（a＞b＞0），焦距为2c．由抛物线方程得焦点，∴c＝．又短轴长为4，∴2b＝4，解得b＝2．∴a2＝b2+c2＝9．∴椭圆C的方程为．（2）假设在x轴上存在一个定点P（t，0）（t≠2）使得PM始终平分∠APB．设直线l的方程为my＝x﹣2，A（x1，y1），B（x2，y2）．联立，化为（9+4m2）y2+16my﹣20＝0，则，．（*）∵PM平分∠APB，∴，∴，化为，把x1＝my1+2，x2＝my2+2代入上式得（2﹣t）（y1﹣y2）[2my1y2+（2﹣t）（y1+y2）]＝0，∵2﹣t≠0，y1﹣y2≠0，∴2my1y2+（2﹣t）（y1+y2）＝0．把（*）代入上式得，化为m（9﹣2t）＝0，由于对于任意实数上式都成立，∴t＝．因此存在点P满足PM始终平分∠APB．（也可以考虑利用k AP+k BP＝0）．23．（14分）已知函数f（x）＝lnx，g（x）＝ax2+2x（1）若曲线y＝f（x）﹣g（x）在x＝1与x＝处的切线相互平行，求a的值及切线斜率．（2）若函数y＝f（x）﹣g（x）在区间（，1）上单调递减，求a的取值范围．（3）设函数f（x）的图象C1与函数g（x）的图象C2交与P、Q两点，过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N，证明：C1在点M处的切线与C2在点N处的切线不可能平行．【解答】解：（1）y＝f（x）﹣g（x）＝，∴y'＝m'（x）＝，则m'（1）＝1﹣a﹣2＝﹣1﹣a，m'（）＝2﹣＝﹣，∵在x＝1与处的切线相互平行，∴m'（1）＝m'（），即﹣1﹣a＝，∴，a＝﹣2，此时切线斜率k＝m'（1）＝﹣1﹣（﹣2）＝2﹣1＝1．（2）∵y＝f（x）﹣g（x）＝，y'＝m'（x）＝，∴函数y＝f（x）﹣g（x）在区间上单调递减，则m'（x）＝≤0恒成立，即成立，∴a，设g（x）＝，则g（x）＝∵x，∴，∴g（x）∈（﹣1，3），∴a≥3．（3）设点P、Q的坐标分别是（x1，y1），（x2，y2），0＜x1＜x2．则点M、N的横坐标为x＝，C1在点M处的切线斜率为k1＝，x＝，k1＝，C2在点N处的切线斜率为k2＝ax+b，x＝，k2＝a+b．假设C1在点M处的切线与C2在点N处的切线平行，则k1＝k2．即，则＝（x22﹣x12）+b（x2﹣x1）＝（x22+bx2）﹣（+bx1）＝y2﹣y1＝lnx2﹣lnx1．∴．设t＝，则lnt＝，t＞1①令r（t）＝lnt﹣，t＞1．则r′（t）．∵t＞1时，r'（t）＞0，∴r（t）在[1，+∞）上单调递增．故r（t）＞r（1）＝0．则lnt＞．这与①矛盾，假设不成立．故C1在点M处的切线与C2在点N处的切线不平行．。

陕西省西工大附中2014年高三适应性训练数学（文）试卷本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分.考试时间120分钟．第Ⅰ卷（选择题 共50分） 一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．集合}}{{2|10,|4,M x gx N x x MN =>=≤=则A ．（0，2）B ．（1，2]C ．（1，2）D ．[1，2] 2.下列函数中，既是奇函数又是增函数的为A ．1y x =+B ．2y x =- C ．1y x =D ．||y x x = 3．设,a b R ∈，i 是虚数单位，则“0ab =”是“复数ba i+为纯虚数”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4．已知圆22:40C x y x +-=，l 过点(3,0)P 的直线，则A ．l 与C 相交B ．l 与C 相切 C ．l 与C 相离 D. 以上三个选项均有可能5.对某商店一个月内每天的顾客人数进行了统计，得到样本的茎叶图（如图所示），则改样本的中位数、众数、极差分别是A ．46，45，56B ．46，45，53C ．47，45，56D ．45，47，536．设向量a =（1,cos θ）与b =（-1，2cos θ）垂直，则cos 2θ等于A ．12 C . 0 D. －17．设函数()xf x xe =，则 A ．x=1为()f x 的极大值点 B ．x=1为()f x 的极小值点C ．x=－1为()f x 的极大值点D ．x=－1为()f x 的极小值点8.阅读右图所示的程序框图，运行相应的程序，输出s 值等于A ．3-B ．10-C ．0D ．2-9.一个几何体的三视图形状都相同，大小均等，那么这个几何体不可以是A ．球B ．三棱锥C ．正方体D ．圆柱10. 小王从甲地到乙地的时速分别为a 和b （a<b ），其全程的平均时速为v ，则2a b + D. v=2a b+ 第Ⅱ卷（非选择题 共100分）二．填空题：本大题共5小题，每小题5分，共25分．将答案填写在题中的横线上． 11.已知关于x 的不等式022>+-a ax x 在R 上恒成立，则实数a 的取值范围是 .12.从点P （2,3）向圆221x y +=作两条切线PA,PB,切点为A ，B ，则直线AB 的方程是 .13. 在三角形ABC 中，角A,B,C 所对应的长分别为a ，b ，c ，若a=2 ，B=6π，b= .14. 右图是抛物线形拱桥，当水面在l 时，拱顶离水面2米，水面宽4米，水位下降1米后，水面宽 米.15. （考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）A.（不等式选做题）若存在实数x 使|||1|3x a x -+-≤成立，则实数a 的取值范围是 .B.（几何证明选做题）如图，在圆O 中，直径AB 与弦CD 垂直，垂足为E ，EF DB ⊥，垂足为F ，若6AB =，1AE =，则 DF DB ⋅= .C.（坐标系与参数方程）直线2cos 1ρθ=与圆2cos ρθ=相交的弦长为 .三．解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤． 16.函数()sin()16f x A x πω=-+（0,0A ω>>）的最大值为3， 其图像相邻两条对称轴之间的距离为2π， （Ⅰ）求函数()f x 的解析式； （Ⅱ）设(0,)2πα∈，则()22f α=，求α的值.17. （本小题满分12分）(Ⅰ)叙述并证明面面垂直性质定理;(Ⅱ)P(00,x y )Ax+By+C=0到直线L:的距离d= ，并证明此公式.18.（本小题满分12分）某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的已知这100位顾客中的一次购物量超过8件的顾客占55％.（Ⅰ）确定x ，y 的值，并估计顾客一次购物的结算时间的平均值； （Ⅱ）求一位顾客一次购物的结算时间不超过．．．2分钟的概率.（将频率视为概率）19. （本题满分12分）已知数列{}n a 中，()112,202,n n a a a n n n N -=--=≥∈. （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设12321111n n n n nb a a a a +++=+++⋅⋅⋅+，求数列{}n b 的通项公式.20. （本题满分13分）已知函数ln ()1xf x ax x=++，（a R ∈） （Ⅰ）若()f x 在定义域上单调递增，求实数a 的取值范围； （Ⅱ）若函数()()g x xf x =有唯一零点，试求实数a 的取值范围．21. （本题满分14分）已知椭圆221:14x C y +=，椭圆2C 以1C 的长轴为短轴，且与1C 有相同的离心率。

2014年陕西省高考数学一模试卷（文科）一、选择题(本大题共10个小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的)1. 已知复数z =(2−i)i （其中i 为虚数单位），则z ¯=( )A 2−iB 1+2iC −1+2iD 1−2i2. 设全集U =R ，A ={x|x x+3<0}，B ={x|x <−1}，则如图中阴影部分表示的集合为（ ）A {x|x >0}B {x|−3<x <−1}C {x|−3<x <0}D {x|x <−1}3. 直线l:mx −y +1−m =0与圆C:x 2+(y −1)2=1的位置关系是（ ）A 相交B 相切C 相离D 无法确定，与m 的取值有关4. 已知α是第四象限的角，若cosα=35，则tan2α=( )A 157B 167C 207D 2475. 函数f(x)=2x+1和函数g(x)=log 2(x +3)的图象的交点一定在（ ）A 第一象限B 第二象限C 第三象限D 第四象限6. 在△ABC 中，“A >B”是“sinA >sinB”的（ ）A 充要条件B 必要不充分条件C 充分不必要条件D 既不充分也不必要条件7. 如果实数x 、y 满足条件{x −y +1≥0y +1≥0x +y +1≤0，那么z =−2x +y 的最大值为（ ）A 1B 2C 3D 48. 已知函数f(x)=(1−3m)x +10（m 为常数），若数列{a n }满足a n =f(n)(n ∈N ∗)，且a 1=2，则数列{a n }前100项的和为（ ）A 39400B −39400C 78800D −788009. 设O 为△ABC 内部的一点，且OA →+OB →+2OC →=0，则△AOC 的面积与△BOC 的面积之比为（ ）A 1B 53C 32D 2 10. 已知点M(−3, 2)是坐标平面内一定点，若抛物线y 2=2x 的焦点为F ，点Q 是该抛物线上的一动点，则|MQ|−|QF|的最小值是（ ）A 72B 3C 52 D 2二、填空题（本大题共4小题，每小题5分，共25分）11. 在区间[20, 80]内任取一个实数m，则实数m落在区间[50, 75]的概率为________．12. 如图所示的算法中，输出的S的值为________．13. 已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的体积为________．14. 设n为正整数，f(n)=1+12+13+...+1n，计算得f(2)=32，f(4)>2，f(8)>52，f(16)>3．观察上述结果，按照上面的规律，可推测f(128)>________．（考生注意：请在下列三个题任选一题作答，如果多做，则按所做的第一题评分）【不等式选做题】15. 若不等式|x+1|+|x−3|≥a+4a对任意的实数x恒成立，则实数a的取值范围是________．【几何证明选做题】16. 如图，A，B是两圆的交点，AC是小圆的直径，D和E分别是CA和CB的延长线与大圆的交点，已知AC=4，BE=10，且BC=AD，则AB=________．【极坐标与参数方程选做题】17. 在极坐标系中，圆ρ=2cosθ的直径等于________．三、解答题（本大题共6小题，共75分.解答应写出文字说明，证明过程或演算过程）18. 已知平面向量a→=(cosφ, sinφ)，b=(cosx, sinx)，其中0<φ<π，且函数f(x)=(a→⋅b →)cosx +sin(φ−x)sinx 的图象过点(π6, 1)．(I)求φ的值；(II)将函数y =f(x)图象向右平移π6，得到函数y =g(x)的图象，求函数y =g(x)递减区间． 19. 已知数列{a n }的前n 项和为S n ，且S n =4a n −3(n ∈N ∗)．（1）证明：数列{a n }是等比数列；（2）若数列{b n }满足b n+1=a n +b n (n ∈N ∗)，且b 1=2，求数列{b n }的通项公式．20. 如图，AC 是圆O 的直径，点B 在圆O 上，∠BAC =30∘，BM ⊥AC 交AC 于点M ，EA ⊥平面ABC ，FC // EA ，AC =4，EA =3，FC =1．（1）证明：AB ⊥BF ；（2）求三棱锥E −BMF 的体积．21. 甲、乙两人参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，画出茎叶图如图所示．（1）指出学生乙成绩的中位数，并说明如何确定一组数据的中位数；（2）现要从中选派一人参加数学竞赛，你认为派哪位学生参加，成绩比较稳定？（3）若将频率视为概率，请预测学生甲在今后一次数学竞赛中成绩高于80分的概率．22. 已知点P(−1, 32)是椭圆C:x 2a 2+y 2b 2=1(a >b >0)上一点，F 1、F 2分别是椭圆C 的左、右焦点，O 是坐标原点，PF 1⊥x 轴．①求椭圆C 的方程；②设A 、B 是椭圆C 上两个动点，满足PA →+PB →=λPO →(0<λ<4，且λ≠2)求直线AB 的斜率．23. 已知函数f(x)＝x −1+ae x （a ∈R ，e 为自然对数的底数）．(Ⅰ)若曲线y ＝f(x)在点（1, f(1)）处的切线平行于x 轴，求a 的值；(Ⅱ)求函数f(x)的极值；(Ⅲ)当a ＝1的值时，若直线l:y ＝kx −1与曲线y ＝f(x)没有公共点，求k 的最大值．2014年陕西省高考数学一模试卷（文科）答案1. D2. B3. A4. D5. B6. A7. C8. B9. A10. C11. 51212. 1713. 16314. 9215. (−∞, 0)∪{2}16. 2√317. 218. 解：f(x)=(cosφcosx+sinφsinx)cosx+sin(φ−x)sinx =cos(φ−x)cosx+sin(φ−x)sinx=cos(φ−2x)把点(π6,1)代入得，cos(φ−2×π6)=1解得：φ=2kπ+π3，又∵ 0<φ<π，∴ φ=π3．(II)将函数y=f(x)图象向右平移π6，得到函数y=cos[2(x−π6)−π3]=cos(2x−2π3)的图象．∴ g(x)=cos(2x−2π3)，由2kπ≤2x−2π3≤2kπ+π，得kπ+π3≤x≤kπ+5π6(k∈Z)，∴ 函数y=g(x)递减区间为[kπ+π3,kπ+5π6](k∈Z)．19. 解：（1）证明：由S n=4a n−3，n=1时，a1=4a1−3，解得a1=1．因为S n=4a n−3，则S n−1=4a n−1−3(n≥2)，所以当n≥2时，a n=S n−S n−1=4a n−4a n−1，整理得a n=43a n−1．又a1=1≠0，所以{a n}是首项为1，公比为43的等比数列．（2）解：因为a n=(43)n−1，由b n+1=a n+b n(n∈N∗)，得b n+1−b n=(43)n−1．可得b n=b1+(b2−b′1)+(b3−b2)+...+(b n−b n−1)=2+1−(43)n−11−43=3(43)n−1−1，(n ≥2)．当n =1时上式也满足条件． 所以数列{b n }的通项公式为b n =3(43)n−1−1．20. 解：（1）证明：∵ EA ⊥平面ABC ，FC // EA ，∴ FC ⊥平面ABC∵ AB ⊂平面ABC∴ FC ⊥AB又∵ AC 是直径，B 在圆上，∴ AB ⊥BC∴ AB ⊥平面BFC又∵ BF ⊂平面BFC∴ AB ⊥BF ．（2）在△ABC 中，∠BAC =30∘，BM ⊥AC 交AC 于点M ，AC =4，∴ BM =√3，三角形EMF 的面积S =12(3+1)×4−12×3×3−12×1×1=3 V E−BMF =V B−EMF =13×3×√3=√3．21. 解：（1）乙中共有8个数据，则位于中间的两个数为83，85，∴ 中位数为12(83+85)=84．（2）甲的平均数为x ¯甲=18(78+79+81+82+84+88+93+95)=85， 乙的平均数为x 乙¯=18(75+80+80+83+85+90+95)=85，∴ x 甲¯=x 乙¯．方差S 甲2=18[(78−85)2+(79−85)2+(81−85)2+(82−85)2+(84−85)2+(93−85)2+(95−85)2]=35.5，方差S 乙2=18[(75−85)2+(80−85)2+(80−85)2+(83−85)2+(90−85)2+(92−85)2+(95−85)2]=41，∵ S 甲2<S 乙2，∴ 甲成绩稳定．故应派甲去参加比赛．（3）由题意得P =68=34．22. 解：①∵ PF 1⊥x 轴，∴ c =1，把点P(−1, 32)代入椭圆的方程得1a 2+94b 2=1，又a 2−b 2=c 2=1，联立解得a 2=4，b 2=3．∴ 椭圆C 的方程为x 24+y 23=1；②设直线y =kx +m ，联立{y =kx +m x 24+y 23=1，化为(3+4k 2)x 2+8kmx +4m 2−12=0，∵ 直线AB 与椭圆有两个不同的交点，∴ △=64k 2m 2−4(3+4k 2)(4m 2−12)>0，化为3+4k 2−m 2>0．(∗)∴ x 1+x 2=−8km 3+4k 2． ∵ 满足PA →+PB →=λPO →(0<λ<4，且λ≠2)，∴ (x 1+1，y 1−32)+(x 2+1，y 2−32)=λ(1,−32)，∴ x 1+x 2+2=λ，y 1+y 2−3=−32λ， 又y 1+y 2=kx 1+m +kx 2+m =k(x 1+x 2)+2m ，∴ k(x 1+x 2)+2m −3=−32(x 1+x 2+2)， ∴ (k +32)(x 1+x 2)+2m =0， ∴ (k +32)×−8km3+4k 2+2m =0，化为m(2k −1)=0，若m =0，则直线AB 经过原点，此时PA →+PB →=2PO →，λ=2，不符合题意，因此m ≠0． ∴ 2k −1=0，解得k =12． 23. （1）由f(x)＝x −1+ae x ，得f′(x)＝1−ae x ，又曲线y ＝f(x)在点（1, f(1)）处的切线平行于x 轴，∴ f′(1)＝0，即1−a e =0，解得a ＝e ．（2）f′(x)＝1−ae x ，①当a ≤0时，f′(x)>0，f(x)为(−∞, +∞)上的增函数，所以f(x)无极值；②当a >0时，令f′(x)＝0，得e x ＝a ，x ＝lna ，x ∈(−∞, lna)，f′(x)<0；x ∈(lna, +∞)，f′(x)>0；∴ f(x)在∈(−∞, lna)上单调递减，在(lna, +∞)上单调递增，故f(x)在x ＝lna 处取到极小值，且极小值为f(lna)＝lna ，无极大值．综上，当a ≤0时，f(x)无极值；当a >0时，f(x)在x ＝lna 处取到极小值lna ，无极大值． (Ⅲ)当a ＝1时，f(x)＝x −1+1e x ，令g(x)＝f(x)−(kx −1)＝(1−k)x +1e x ，则直线l:y ＝kx −1与曲线y ＝f(x)没有公共点，等价于方程g(x)＝0在R 上没有实数解．假设k >1，此时g(0)＝1>0，g(1k−1)＝−1+1e 1k−1<0，又函数g(x)的图象连续不断，由零点存在定理可知g(x)＝0在R上至少有一解，与“方程g(x)＝0在R上没有实数解”矛盾，故k≤1．>0，知方程g(x)＝0在R上没有实数解，又k＝1时，g(x)=1e x所以k的最大值为1．。

2014年普通高等学校招生全国统一考试西工大附中第一次适应性训练文科综合能力测试本试卷分第I卷（选择题）和第II卷（非选择题）两部分。

共300分。

第I卷（选择题共140分）本卷共35个小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

云南省已经成为我国最大出口型反季节蔬菜生产基地，其产品因类型丰富而远销新加坡及港、澳、台等地区。

读图1，完成1—3题。

1．云南省蔬菜品种丰富，是得益于自然条件的A．气温较高 B．地形起伏大C．降水较丰沛 D．土壤较肥沃2．春节前，从云南运往香港的蔬菜需要A．采用保鲜技术 B．采用防冻措施C．全部航空运输 D．清除农药残留3．每年春节前，新加坡超市蔬菜三分之一来自云南，一半来自泰国和越南。

与云南相比，泰国和越南抢占新加坡蔬菜市场的优势是A．劳动力廉价 B．热量充足C．品种众多 D．运输成本低图2为我国某自然保护区水系(图甲）及植被带（图乙）分布状况，据此完成4—6题4．该自然保护区的面积约为A.1140Km2B.1350Km2C.1100Km2D.1520Km25．关于该自然保护区的说法正确的是A.阴坡为迎风坡，阳坡为背风坡B.阳坡坡度大于阴坡C.阴坡植被总量大于阳坡D.阳坡面积大于阴坡6．该自然区位于A. 南岭B.秦岭C.天山D.长白山图4为1982年和2009年我国人口年龄结构统计图。

读图完成7—8题。

7．图中信息反映出A.1982-2009年人口出生率呈上升趋势B.1982年的人口平均年龄比2009年的高C.1982年的40岁及以上人口比重比2009年的低D.1982年的20—24岁年龄组人口数量比2009年的多8．由信息可知，与1982年相比，2009年我国人口年龄结构的变化A.显示男女性别比例失调B.意味着社会已经步入老龄化C.表明25—29岁劳动力资源数量下降D.已经影响劳动人口的职业构成图4示意今年9月份第19号超强台风“天兔”登陆路径,读图4,完成9—11题.9．甲地风力初始达到7级时,北京时间为A．9月22日2：00 B．9月21日20：00C．9月22日8：00 D．9月22日14：0010．9月21日至22日，甲地风向变化全过程为A．西北→东北 B．东南→西南C．东南→偏南→西南→偏西 D．西北→偏北→东北→偏东11．当台风中心位于位置1时，下列城市风力最大的是A．厦门 B．香港 C．高雄 D．海口12．2012年某商品的价格为24元。

【解析】陕西省西工大附中2014届高三上学期第四次适应性训练数学（文）试题1．复数151i（i 为虚数单位）的值为（ ）A.iB. 1C.i -D.1-【答案】A【 解析】153111i i i i==-=.2．已知{},01|2>-=x x A {}1,0,1,2--=B ，则()R C A B ⋂= （ ）A.{}2,1--B. {}2-C. {}1,0,1-D. {}0,1【答案】C【 解析】因为{}{}2|10|11,A x x x x x =->=><-或{}1,0,1,2--=B ，所以()R C A B ⋂={}1,0,1-.3．1x =是2320x x -+=的（ ）条件A. 充分不必要B. 必要不充分C.充要D.既不充分又不必要 【答案】A【 解析】因为方程2320x x -+=的根为1和2，所以1x =是2320x x -+=的充分不必要条件。

4．将函数sin()3y x π=-的图象上所有点的横坐标伸长到原的2倍（纵坐标不变），再将所得的图象向左平移3π个单位，得到的图象对应的解析式是（ ）A. 1sin 2y x =B. 1sin()22y x π=-C. 1sin()26y x π=-D. sin(2)6y x π=-【答案】C【 解析】将函数sin()3y x π=-的图象上所有点的横坐标伸长到原的2倍（纵坐标不变），得到函数1sin()23y x π=-的图像，再将所得的图象向左平移3π个单位，得到的图象对应的解析式是11sin sin()23326y x x πππ⎡⎤⎛⎫=+-=- ⎪⎢⎥⎝⎭⎣⎦。

5. 某几何体的主视图与左视图都是边长为1的正方形，且体积为12，则该几何体的俯视图可以是（ ）A. B ． C. D ．【答案】C【 解析】当俯视图是A 时，正方体的体积是1；当俯视图是B 时，该几何体是圆柱，底面积2124S ππ⎛⎫=⨯= ⎪⎝⎭，高为1，则体积是4π；当俯视图是C 时，该几何体是直三棱柱，故体积是1111122V =⨯⨯⨯=；当俯视图是D 时，该几何体是圆柱切割而成，其体积是21144V ππ=⨯⨯=。

2014年普通高等学校招生全国统一考试适应性训练数 学(文科)本试卷分为第1卷〔选择题〕和第2卷〔非选择题〕两局部，总分为150分。

考试时间120分钟第1卷〔选择题 共50分〕一．选择题：本大题共10小题，每一小题5分，共50分．在每一小题给出的四个选项中，只有一项为哪一项符合题目要求的。

1.设集合{}{}{}1,2,3,4,5,|,,,A B M x x a b a A b B ====+∈∈如此M 中元素的个数为〔A 〕3 〔B 〕4 〔C 〕5 〔D 〕62.()3=〔A 〕8-〔B 〕8〔C 〕8i -〔D 〕8i3.向量()()()()1,1,2,2,,=m n m n m n λλλ=+=++⊥-若则〔A 〕4-〔B 〕-3〔C 〕2-〔D 〕-14.函数()()-1,0(21)f x f x +的定义域为，则函数的定义域为〔A 〕()1,1-〔B 〕1(1,)2--〔C 〕()-1,0〔D 〕1,12⎛⎫⎪⎝⎭5. 某单位有840名职工, 现采用系统抽样方法, 抽取42人做问卷调查, 将840人按1, 2, …, 840随机编号, 如此抽取的42人中, 编号落入区间[481, 720]的人数为 (A) 11(B) 12(C) 13(D) 146.数列{}n a 满足{}12430,,103n n n a a a a ++==-则的前项和等于〔A 〕()-10-61-3〔B 〕()-1011-39〔C 〕〔D 〕()-1031+3 7.抛物线()2:82,2,C C y x M k C =-与点过的焦点，且斜率为的直线与交于,0,A B MA MB k ==两点,若则〔A 〕12〔B 〔C 〔D 〕28.椭圆2212:1A A 43x y C +=的左，右顶点分别为 ，，点P 在C 上，且直线斜率的取值范围是[]12,1,PA --那么直线斜率的取值范围是〔A 〕3384⎡⎤⎢⎥⎣⎦，〔B 〕1324⎡⎤⎢⎥⎣⎦，〔C 〕112⎡⎤⎢⎥⎣⎦，〔D 〕314⎡⎤⎢⎥⎣⎦， 9.假设函数211()+2f x x ax x ⎛⎫=++∞ ⎪⎝⎭在，是增函数，如此实数a 的取值范围是 〔A 〕〔B 〕[]-∞1，〔C 〕[]0，3〔D 〕[]3∞，+ 10.函数()cos sin 2f x x x =,如下结论错误的答案是〔A 〕()(),0y f x π=的图像关于中心对称〔B 〕〔C 〕()32f x 的最大值为〔D 〕()f x 既是奇函数，又是周期函数二、填空题：〔本大题共5小题，每一小题5分，共25分。

2014年普通高等学校招生全国统一考试西工大附中第一次适应性训练数 学（理科）第Ⅰ卷 选择题（共50分）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（本大题共10小题，每小题5分，共50分）1．()3=（ ）A ．8-B ．8C ．8i -D ．8i 【答案】A【解析】()))33211=++=-+。

2．若向量a ，b r 满足||1a =，||b =()a a b ⊥+r ，则a r 与b r 的夹角为（ ）A ．2πB ．23πC ．34πD ．56π【答案】C【解析】因为()a a b ⊥+r r r ，所以2()0,0a a b a a b ⋅+=+⋅=r r r r r r即，所以1a b ⋅=-r r，所以cos ,2a b a b a b⋅==-⋅r rr r r r ，所以a r 与b r 的夹角为34π。

3．522x ⎫⎪⎭-的展开式中常数项是（ ）A ．5B ．5-C ．10D ．10-【答案】D【解析】由()()55522555522,0,12rr rrr r r C xC xr ----=-==若则，所以()52=-10rr C -。

4.把函数f (x )的图象向右平移一个单位长度，所得图象恰与函数xy e =的反函数图像重合，则f (x )=（ ）A. ln 1x -B. ln 1x +C. ln(1)x -D. ln(1)x + 【答案】D【解析】依题意，f (x ) 向右平移一个单位长度之后得到的函数是ln y x =，所以()ln(1)f x x =+。

5．已知三棱柱ABC-A1B1C1的侧棱与底面垂直，体积为94的正三角形，若P 为底面A1B1C1的中心,则PA 与平面ABC 所成角的大小为( )A ．512πB ．3πC ．4πD ．6π【答案】B【解析】因为三棱柱ABC-A1B1C1的侧棱与底面垂直，体积为94，底面是边长为3的正三角形，所以()23933,442h h ⨯==所以，设O 为底面ABC 的中心,连接AO ，OP ，则OP ⊥底面ABC ，所以∠PAO 即为PA 与平面ABC 所成角，又易知AO=1，OP=32，所以tan ∠PAO=3OP AO =PA 与平面ABC 所成角的大小为3π。