作业2-轴对称问题的平衡微分方程推导

弹性力学总结第一章绪论一、弹性力学的内容：弹性力学的研究对象、内容和范围。

二、弹性力学的基本量1、外力（1）体力（2）面力2、内力——应力3、应变4、位移以上基本量要求掌握其定义、表达式、分量的符号、正负号规定、量纲。

三、弹性力学中的基本假定1、连续性2、完全弹性3、均匀性4、各向同性以上是对材料性质的假定，凡符合以上四个假定的物体，称为理想弹性体。

5、小变形假定（对物体的变形状态所作的假定）要求掌握各假定的内容和意义（在建立弹性力学基本方程时的作用）。

习题举例：1、弹性力学，是固体力学的一个分支，它的任务是研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的（），从而解决各类工程中所提出的强度、刚度和稳定问题。

A．应力、应变和位移；B．弯矩、扭矩和剪力；C．内力、挠度和变形；D．弯矩、应力和挠度。

2、在弹性力学中，作用于物体的外力分为（）。

A．体力和应力；B．应力和面力；C．体力和面力；D．应力和应变。

3、重力和惯性力为（C ）。

A ．应力；B ．面力；C ．体力；D ．应变。

4、分布在物体体积内的力称为（ C ）。

A ．应力；B ．面力；C ．体力；D ．应变。

5、物体在体内某一点所受体力的集度的表达式及体力分量的量纲为（ A ）。

A ．0lim V F f V∆→∆=∆，-2-2L MT ； B ．0lim S F f S ∆→∆=∆，-1-2L MT ； C ．0lim A F p A ∆→∆=∆，-1-2L MT ； D ．0lim V F f V ∆→∆=∆，-1-2L MT 。

6、弹性力学研究中，在作数学推导时可方便地运用连续和极限的概念，是利用了（ ）假定。

A ．完全弹性；B ．连续性；C ．均匀性；D ．各向同性。

7、（ A ）四个假设是对物体的材料性质采用的基本假设，凡是符合这四个假设的物体，就称为理想弹性体。

A ．完全弹性，连续性，均匀性和各向同性；B ．完全弹性，连续性，均匀性和小变形；C ．连续性，均匀性，各向同性和小变形；D ．完全弹性，连续性，小变形和各向同性。

题提示和答案《弹性力学简明教程》习题提示和参考答案第二章习题的提示与答案2－1 是2－2 是2－3 按习题2－1分析。

2－4 按习题2－2分析。

2－5 在的条件中，将出现2、3阶微量。

当略去3阶微量后，得出的切应力互等定理完全相同。

2－6 同上题。

在平面问题中，考虑到3阶微量的精度时，所得出的平衡微分方程都相同。

其区别只是在3阶微量（即更高阶微量）上，可以略去不计。

2－7 应用的基本假定是：平衡微分方程和几何方程─连续性和小变形，物理方程─理想弹性体。

2－8 在大边界上，应分别列出两个精确的边界条件；在小边界（即次要边界）上，按照圣维南原理可列出3个积分的近似边界条件来代替。

2－9 在小边界OA边上，对于图2－15（a）、（b）问题的三个积分边界条件相同，因此，这两个问题为静力等效。

2－10 参见本章小结。

2－11 参见本章小结。

2－12 参见本章小结。

2－13 注意按应力求解时，在单连体中应力分量必须满足（1）平衡微分方程，（2）相容方程，（3）应力边界条件（假设)。

2－14 见教科书。

2－15 见教科书。

2－16 见教科书。

2－17 取它们均满足平衡微分方程，相容方程及x=0和的应力边界条件，因此，它们是该问题的正确解答。

2－18 见教科书。

2－19 提示：求出任一点的位移分量和，及转动量，再令,便可得出。

第三章习题的提示与答案3－1 本题属于逆解法，已经给出了应力函数，可按逆解法步骤求解：（1）校核相容条件是否满足，（2）求应力，（3）推求出每一边上的面力从而得出这个应力函数所能解决的问题。

3－2 用逆解法求解。

由于本题中l>>h, x=0,l 属于次要边界（小边界），可将小边界上的面力化为主矢量和主矩表示。

3－3 见3-1例题。

3－4 本题也属于逆解法的问题。

首先校核是否满足相容方程。

再由求出应力后，并求对应的面力。

本题的应力解答如习题3-10所示。

应力对应的面力是：主要边界：所以在边界上无剪切面力作用。

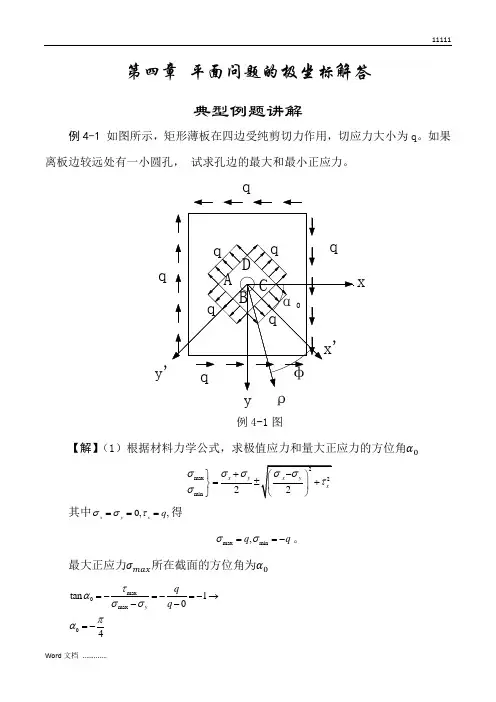
第四章 平面问题的极坐标解答典型例题讲解例4-1 如图所示，矩形薄板在四边受纯剪切力作用，切应力大小为q 。

如果离板边较远处有一小圆孔， 试求孔边的最大和最小正应力。

例4-1图【解】（1）根据材料力学公式，求极值应力和量大正应力的方位角max min 2x y σσσσ+⎫=⎬⎭ 其中0,,x y x q σστ===得max min ,q q σσ==-。

最大正应力 所在截面的方位角为max 0max 0tan 104yqq τασσπα=-=-=-→--=-qqx若在该纯剪切的矩形薄板中，沿与板边成方向截取矩形ABCD ，则在其边界上便承受集度为q 的拉力和压力，如图所示。

这样就把受纯剪切作用的板看作与一对边受拉，另一对边受压的板等效。

（2）取极坐标系如图。

由2222442222cos 2(1)(13),cos 2(13),(4-18)sin 2(1)(13).ρφρφr r σq φρρr σq φρr r τq φρρ⎫=--⎪⎪⎪⎪=-+⎬⎪⎪=--+⎪⎪⎭得矩形薄板ABCD 内的应力分量为()()()2222442222cos 2(1)(13)cos 2(13)sin 2(1)(13)ρφρφa a σq φa ρρa σq φb ρa a τq φc ρρ=--=-+=--+ 其中 为小孔的半径，而孔边最大与最小正应力由式（b ），在 处得到44cos 2(13)4cos 2,φa σq φaϕ=-+=-当 ， 时，孔边最小正应力为，当时，孔边最大正应力为。

分析：矩形板ABCD 边界上各点的应力状态与板内无孔时的应力状态相同。

也可以应用叠加法，求解薄板的各种较复杂的平面应力（应变）问题。

习题全解4-1试比较极坐标和直角坐标中的平衡微分方程、几何方程和物理方程，指出哪些项是相似的，哪些项是极坐标中特有的？并说明产生这些项的原因。

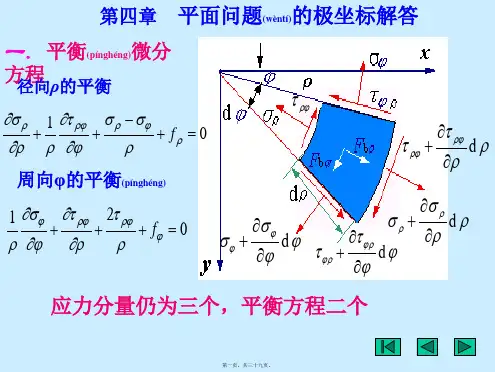
【解】 （1）极坐标，直角坐标中的平衡微分方程10210f f ρρϕρϕρρϕϕρϕϕστσσρρϕρτστρρϕρ∂∂-⎧+++=⎪∂∂⎪⎨∂∂⎪+++=⎪∂∂⎩ 00yxx x y xy yf xy f y x τσστ∂⎧∂++=⎪∂∂⎪⎨∂⎪++=⎪∂∂⎩将极坐标中的平衡微分方程与直角坐标中的平衡微分方程相比较，第一式中，前两项与直角坐标相似；而项是由于正 面上的面积大于负 面上的面积而产生的，是由于正负 面上的正应力 在通过微分体中心的 方向有投影而引起的。

轴对称应力状态分析当作用力对称分布于回转体时，其内部的应力状态称为轴对称应力状态，轴对称应力状态的特点是:(1)通过旋转体轴线的子午面在变形过程中始终不会扭曲，所以在θ面上没有剪应力，即pθτ=Zθτ=0，所以θσ就是一个主应力。

（2）各应力分量与θ坐标无光，对θ的偏导数为零。

采用圆柱坐标系时，轴对称的应力张量为：ij 0=000P ZPP ZZ θσσσσ⎛⎫ ⎪ ⎪ ⎪⎝⎭ττ设点a 的坐标为（P ,θZ)，应力状态为ijσ，a 1的坐标为（p p d +，d θθ+，z z d +），应力状态为ij ijd σσ+，即z z z ij ij z zzzzzz z z=zzz z d d d d d d d d d d θθθθθθθθθθσσθθσσσσθθσθσθ∂∂∂⎛⎫+++⎪∂∂∂⎪∂∂∂ ⎪++++ ⎪∂∂∂⎪∂∂∂ ⎪+++ ⎪∂∂∂⎝⎭ρρρρρρρρρρττρττρτττρτρτττρτρ 根据力的平衡条件=P ∑ρ0；=0P θ∑；=0Z P ∑，可得以下圆柱坐标系的平衡微分方程为：z zzz 0z 0z θσσσσ∂∂-⎫++=⎪⎪∂∂⎬∂∂⎪++=⎪∂∂⎭ρρρρρτρρττρρ在有些轴对称问题（例如圆柱体的均匀镦粗、挤压和拉拔等）中，由于=d d ρθεε，由增量理论可知，当某两个正应变增量的分量相等时，其对应的应力也相等，所以=ρθσσ。

那么轴对称的平衡方程可简化为：z zz z =0z =0z ρρρρσρσρρ∂∂⎫+⎪∂∂⎪⎬∂∂⎪++⎪∂∂⎭τττ轴对称的屈服应力： 1 Tresca 屈服准则Tresca 认为当最大剪应力达到某定值时材料就会发生屈服，开始塑性变形阶段，即 max cτ=，由于屈服时的定值c 与应力状态无光，故可由单周俊宇拉伸实验或薄壁管扭转实验确定。

单向均匀拉伸中230σσ==，屈服时1sσσ=，所以最大剪应力为：13113222scσσσστ-====，该剪应力也应等于纯剪屈服时的剪应力k ，所以当假定 123σσσ≥≥，塑性条件可写成31==2ks σσσ-，该公式同样可用于轴对称问题中。

空间轴对称问题的基本微分方程在描述轴对称问题各分量时，用圆柱坐标r 、θ、z 比用直角坐标x 、y 、z 方便得多，如以z 轴为对称轴，如图1所示则所有应力分量、应变分量和位移分量都将只是r 和z 的函数，不随θ而变。

如图，取微小六面体。

注意到应力分量是（r ，z ）将各面上的应力分量写出。

单位体积内的体积力在r 、z 方向的分量分别表示为r f 、z f 。

根据单元体在r和z 方向的平衡方程，略去高阶微量，同时除以rdrd dz θ，因为d θ很小，近似认为()sin 22d d θθ≈，加以整理后得到r 方向和z 方向的平衡微分方程为： 图1柱坐标下微小六面体r r z 0r 0zr r rz rz z f z rf z r r θστσσσττ∂∂-⎫+++=⎪⎪∂∂⎬∂∂⎪+++=⎪∂∂⎭公式（1） 进一步推导空间轴对称问题的几何变形方程：设u 、w 分别代表r 及z 轴方向的位移分量，由极坐标内位移与应变的关系以及直角坐标的关系式，很容易得到r u r ∂∂=ε，r u =θε，z w z ∂∂=ε，0==z r θθγγ，rw z u rz ∂∂+∂∂=γ 公式（2） 最后，根据广义胡克定律，可得出物理方程：1[()]1[()]1[()]2(1)r r z r z z z r rz rz rz EEEG E θθθθεσμσσεσμσσεσμσστμγτ⎫=-+⎪⎪⎪=-+⎪⎬⎪=-+⎪⎪+==⎪⎭公式（3） 或 ()()2112112()()2112112()()2112112()2(1)2(1)r r r z z z rz rz rz E E u e e e G r E E u e e e G r E E w e e e G z E E u w G z rθθθμμσελεμμμμμμσελεμμμμμμσελεμμμμτγγμμ∂⎫=+=+=+⎪+-+-∂⎪⎪=+=+=+⎪+-+-⎪⎬∂⎪=+=+=+⎪+-+-∂⎪∂∂⎪==+=⎪++∂∂⎭ 公式（4） 式中，r z u u w e r r z θεεε∂∂==++∂∂++为体积应变。

平衡微分方程推导过程平衡微分方程，听上去是不是很复杂？但其实它就像一杯混合了各种果汁的饮料，调和得好喝，调和得不好就苦涩难咽。

咱们今天就来聊聊这个神奇的东西，让它不再那么神秘，轻松搞定。

微分方程可不是外星人的语言，而是我们描述变化的工具。

想想吧，生活中处处都有变化，时间在走，温度在升，心情在起伏。

微分方程就像一个记录这些变化的日记，帮我们把这些故事讲出来。

平衡微分方程则是这个故事中的主人公，特别关注系统在特定条件下如何达到一种稳定的状态。

就像是你在阳台上浇花，水多了，花儿会淹死；水少了，花儿又会干死。

适量的水才能让花儿茁壮成长，这就是平衡的美妙之处。

在数学的世界里，平衡微分方程通常以一种简洁的形式出现。

想象一下，咱们有一个方程，里面有变量和常数，像调料一样。

我们通常会看到类似这样的一种形式：dy/dt = f(y)，其中dy/dt表示随时间变化的东西，f(y)则是我们要研究的变化率。

很简单吧？就像煮汤，先把水煮开，再加点盐，最后加点青菜。

这个f(y)就是咱们汤里的调味料，关键在于它如何影响整个汤的味道。

好啦，接下来就让我们来玩一个小游戏。

想象一下你有一个气球，你不停地往里吹气。

最开始，气球鼓起来的速度很快，过了一段时间，气球的膨胀速度会慢下来，直到最终达到一个平衡点。

这个过程就可以用平衡微分方程来描述。

乍一看好像是个无聊的过程，但其实每一秒都有故事发生。

气球的表面张力、空气的压强、你的嘴巴的力量，都是这个故事里的角色。

把这些因素放到微分方程里，最终得到的就是平衡方程。

一旦我们写下了这些微分方程，接下来就是解它。

别紧张，解微分方程就像解谜一样，慢慢来，细心点。

我们会找到一个叫做平衡点的地方，没错，就是那些让系统保持稳定的点。

可以想象成是一座山的山顶，只有到达那个点，才能看到美丽的风景。

平衡点通常是让dy/dt等于零的地方，也就是那种你不需要再费劲去加水的状态。

解决微分方程时，我们可能需要使用一些技巧，比如分离变量法，或者是代数方法，听上去是不是很高深？其实这些方法就像是厨房里的工具，有刀有勺，总有一种适合你。

二 平衡微分方程的积分形式分别对流体平衡微分方程乘dz dy dx ,,相加，则有)(Zdz Ydy Xdx dz zp dy y p dx x p ++=∂∂+∂∂+∂∂ρ 取全微分 )(Z d z Y d y X d x dp ++=ρ根据数学原理，=ρconst 时，)(Zdz Ydy Xdx ++必须为某标量函数的全微分。

设标量函数为W ，则有)(dz zWdy y W dx x W dW dp ∂∂+∂∂+∂∂==ρρ Z zWY y W X x W =∂∂=∂∂=∂∂,, 由上式可知，),,(z y x W 是描述质量力的标量函数，称为力势函数。

由势函数决定的力称为有势力。

重力作用的空间称为重力场,为有势场。

积分式（2.2-10），则有c W p +=ρ (*)若某点（000,,z y x ）势函数为0W 时压强为0p ，则00W p c ρ-=，则)(00W W p p -+=ρ三 流体静力学基本方程a 、自由液面上的正向坐标系b 、自由液面上的反向坐标系c 、自由液面下0z 处的正向坐标系图 2-5 静止液体在不同坐标系的势能① *式即是流体静力学的基本方程，在图2-5（a ）中，取0===z y x ，00=W ，a p p =0；单位质量的液体势能gz W -=（z 与g 反向），则有gz p p a ρ-=注意到h z =-，则有h p gh p p a a γρ+=+=② 在图2-5(b)中，在0===z y x 点，00=W ，a p p =0，在坐标ｚ单位质量势能为gz W =，则有h p gz p p a a γρ+=-+=)0(③ 在图2-5(c)中，边界条件为：0===z y x ，势函数00=W ，gz W -=（z 与g 反向）；则有z p W p p γρ-=+=00另一边界条件为a p p z z y x ====,,00，势函数0gz W -=,由式(2.2-16)可得0000z p gz p p a γρ-=-=则有 h z z z z p p a γγγγ=-=+-=-)(00，即h p p a γ+=通过如上分析可知：c W p +=ρ是一般表达式，更一般的表达式：=+γpz const =+=+γγ2211p z p z const证明如下：参看图2-6图 2-6 流体中两点压差11h p p a γ+= 22h p p a γ+=由上两式则有)()(122121z z h h h p p -=∆=-=-γγγ移项则有⇒⇒+=+2211z p z p γγ γγ2211p z p z +=+由于1z 和2z 的任意性，故有⇒⇒=+=+const p z p z γγ2211 const pz =+γ几何含义：在静止流体中单位重量的流体的压力能γ/p 和位置势能z 可以互相转化，总和不变。