流体的平衡微分方程及其积分

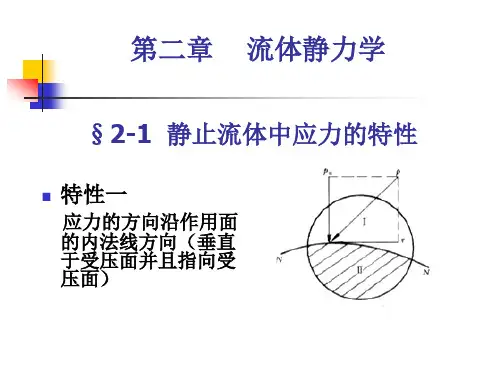
学习单元二、静压强分布规律 一、 流体静力学平衡微分方程 在静止流体中任取一边长为 d x ，d y 和d z 的微元平行六面体的流体微团，如下图所示。

现在来分析作用在这流体微团上外力的平衡条件。

由上节所述流体静压强的特性知，作用在微元平行六面体的表面力只有静压强。

设微元平行六面体中心点处的静压强为p ，则作用在六个平面中心点上的静压强可按泰勒（G.I.Taylor ）级数展开，例如：在垂直于X 轴的左、右两个平面中心点上的静压强分别为：⋅⋅⋅+⎪⎭⎫ ⎝⎛∂∂-⎪⎭⎫ ⎝⎛∂∂+∂∂-3332222d 612d 212d x x p x x p x x p p ⋅⋅⋅+⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+∂∂+3332222d 612d 212d x x p x x p x x p p 略去二阶以上无穷小量后，分别等于x x p p d 21∂∂-和x x p p d 21∂∂+由于平行六面体是微元的，所以可以把各微元面上中心点的压强视为平均压强。

因此，垂直于x 轴的左、右两微元面上的总压力分别为：z y x x p p d d d 21⎪⎭⎫ ⎝⎛∂∂-与z y x x p p d d d 21⎪⎭⎫ ⎝⎛∂∂+同理，可得到垂直于y 轴的下、上两个微元面上的总压力分别为z x y p p d d dy 21⎪⎪⎭⎫ ⎝⎛∂∂-以及z x y y p p d d d 21⎪⎪⎭⎫ ⎝⎛∂∂+垂直于z 轴的后、前两个微元面上的总压力分别为y x z p p d d dz 21⎪⎭⎫ ⎝⎛∂∂-，y x z z p p d d d 21⎪⎭⎫ ⎝⎛∂∂+流体微团上的外力除静压强外，还有质量力。

若流体微团的平均密度为ρ，则质量力沿三个坐标轴的分量分别是：z y x f x d d d ρz y x f y d d d ρz y x f z d d d ρ静止状态下的微元平行六面体的流体微团的平衡条件是：作用在其上的外力在三个坐标轴上的分力之和都等与零。

第一章 绪 论一、连续介质的概念将流体认为是充满其所占据空间无任何孔隙的质点所组成的连续体。

二、液体的主要物理性质（1）惯性、质量、密度（2）压缩性（热胀性）与表面张力特性压缩性：流体受压，体积缩小，密度增大的性质； 热胀性：流体受热，体积膨胀，密度减小的性质。

1、对于液体液体的压缩性一般用压缩系数β来表示。

如对液体体积V ，密度ρ，压强增大dp ，密度增大ρd ， 压缩系数的定义：dpd ρρβ=压缩系数： dpV dV -=β 单位：N m /2弹性模量：dVdp Vd dp d dp E -====ρρρρβ1单位：2/m N热胀系数：dTV dV dTd =-=ρρα， 单位：1-T注：水的热胀性和压缩性非常小，一般可以忽略不计，在某些情况下才需要考虑：水击，热水采暖。

2、对于气体，气体的压缩性和热胀性比较显著。

服从理想气体状态方程：RT p =ρ适用范围：气体的长距离运输以及气体的高速流动中需要考虑气体的压缩性。

（3）粘滞性 dydu A T μτ==dtd dydu θ=（1）上式表明，速度梯度等于直角变形速度。

（3）μ——动力粘滞系数，单位：)/(2s m N ⋅，s Pa ⋅。

含义：单位速度梯度下的切应力。

表现粘滞力的动力性质。

ρμν/=——运动粘滞系数，单位：s cm /2（斯托克斯，St ）含义：单位速度梯度作用下的切应力对单位体积质量作用产生的阻力加速度。

（4）流体的粘滞系数都会随着温度的变化而变化，但对压强的变化在一定范围内不敏感。

水和空气的粘滞系数随温度变化的规律是不同的，是因为粘滞性是分子间的吸引力和分子不规则热运动产生动量交换的结果。

（5）满足牛顿内摩擦定律的流体称为牛顿流体（本书重点）；否则是非牛顿流体。

三、理想流体与实际流体模型不考虑粘性作用的流体，称为无粘性流体（或理想流体）。

四、质量力、表面力表面力：AP p A A ∆∆=→∆lim（压强），AT A A∆∆=→∆limτ（切应力）质量力：k Z j Y i X dmF d f++== 2/s m 第二章 流体静力学 第一节 流体静压强及其特性一、流体静压强的定义 A Pp aA ∆∆=→∆l i m二、流体静压强的特性（1） 流体静压强的方向是垂直指向受压面的（正压性）；（2） 流体静压强的无方向性：在同一点各方向的静压强大小与受压面方位无关。

流体的平衡微分方程及其积分一、流体平衡微分方程——欧拉平衡方程如图所示，在平衡流体中取一微元六面体，边长分别为d x ，d y ，d z ，设中心点的压强为p (x,y,z )=p ，对其进行受力分析：根据平衡条件，在x 方向有0F x＝∑，即： 0zX y z y xp 21z y ）21＝＋）＋－（（d dxd d d dx p d d dx x p p ρ∂∂∂∂- 01X ＝－xp ∂∂ρ 式中：X ——单位质量力在x 轴的投影流体平衡微分方程（即欧拉平衡微分方程）： ⎪⎪⎪⎭⎪⎪⎪⎬⎫=∂∂-=∂∂-=∂∂-010101z p Z y p Y x p X ρρρ 物理意义：处于平衡状态的流体，单位质量流体所受的表面力分量与质量力分量彼此相等。

压强沿轴向的变化率（zp y p x p ∂∂∂∂∂∂，，）等于轴向单位体积上的质量力的分量（ρX ，ρY ，ρZ ）。

二、平衡微分方程的积分将欧拉平衡微分方程中各式，分别乘以dx 、dy 、dz ，整理： Zdz)Y dy (Xdx dz zp dy y p x ++=∂∂+∂∂+∂∂ρdx p 因为p = p (x,y,z )∴ Zdz)Ydy (Xdx dp ++=ρ ρ为常量；Xdx ＋Ydy ＋Zdz 应为某函数W ＝F （x ，y ，z ）的全微分： dz zW dy y W dx x W dz dy dx d ∂∂+∂∂+∂∂=++=)Z Y (X W dW dp ＝ρ 平衡流体中压强p 的全微分方程 积分得：p=ρW ＋c假定平衡液体自由面上某点（x 0，y 0，z 0）处的压强p 0及W 0为已知，则： c ＝p 0-ρW 0∴ p=p 0+ρ（W-W 0） 欧拉平衡微分方程的积分三、帕斯卡定律处于平衡状态下的不可压缩流体中，任意点M 处的压强变化值△p 0，将等值地传递到此平衡流体的其它各点上去。

说明：只适用于不可压缩的平衡流体；盛装液体的容器是密封的、开口的均可。