大学物理学教学中初相位的求解_旋转矢量法

旋转矢量求波动方程初相位波动方程是描述波动传播的数学模型，在物理学中有着广泛的应用。

而确定波动方程的初相位，也就是波动的起始状态，对于理解波动的性质和特点起着重要的作用。

在研究波动方程的初相位之前，我们先了解一下什么是旋转矢量。

旋转矢量是指在空间中旋转方向和角度都确定的向量，它可以用来表示物体在空间中的旋转状态。

在电磁波的研究中，旋转矢量常常用来描述电磁波的偏振状态。

当电磁波传播时，光束中的光子会随着波动的传播而发生旋转。

这种旋转可以用旋转矢量来描述，它的大小和方向表示了波动的相位和偏振方向。

因此，确定波动方程的初相位就是确定旋转矢量的大小和方向。

在确定波动方程的初相位时，我们可以通过将电磁波的传播方向与垂直方向的夹角来确定旋转矢量的方向。

而旋转矢量的大小可以根据波动的振幅来确定。

波动的振幅表示了波动的强度，它越大，表示波动的能量越强。

除了振幅和传播方向外，确定波动方程的初相位还与波动的频率有关。

频率表示了波动的周期性，它与波长之间有一个固定的关系。

我们可以通过波动的频率来确定旋转矢量的速度，从而确定初相位。

总结起来，确定波动方程的初相位需要考虑波动的振幅、传播方向和频率。

通过将电磁波的传播方向与垂直方向的夹角确定旋转矢量的方向，再根据波动的振幅和频率确定旋转矢量的大小和速度，就可以确定波动方程的初相位。

确定波动方程的初相位对于研究波动的行为和性质具有重要的意义。

它可以帮助我们理解波动的传播机制以及与其相关的物理现象。

在实际应用中，通过确定波动方程的初相位，我们可以更好地控制和调整波动的特性，为光通信、雷达、医学成像等领域的技术发展提供有力支持。

通过对旋转矢量和波动方程初相位的探讨，我们可以更深入地理解波动现象的本质和特点。

这不仅是对物理学的研究有着重要的指导意义，也是为我们更好地理解和应用波动方程提供了有力的支撑。

我们期待在未来的研究中，能够进一步深化对波动方程初相位的认识，以推动科学技术的进步和发展。

P H ASE OF FO R CED VIBRATI O N BY R OTATING VECTO RXu You w en Xu D i yu( D epa r t ment of Physics , S ichua n Vocatio n al and Technical College , S ui n i n g , S ichuan 629000)Abstract A cco r d i n g to t h e dyna m ic a n d ki n e matic equatio n s of fo r ced vi b ratio n , t h e a mp li2 t u de a n d i n itial p h a s e of fo rce d vi b ratio n a r e o b t a i n ed .K ey Words fo rced vi b ratio n ; ro t a ti n g vecto r ; a m p lit u de ; i n itial p ha s e系统在周期性外力作用下被强迫进行的振动,称为受迫振动. 受迫振动是工程技术中常见的振动. 研究受迫振动具有很大的意义. 求解受迫振动达到稳定状态时的振幅和初相, 一般书籍[ 1～6 ] 都是通过求解受迫振动的动力学方程而得出的,本文用旋转矢量法求受迫振动的振幅和初相.图 1受迫振动的动力学方程旋转矢量受迫振动所受的作用力有:准弹性力- k x 、如图1 所示,从O x坐标轴的原点O , 作一矢量 A ,其长度A 等于谐振动的振幅; t = 0 时 A 与O x 轴夹角等于初相φ; 并使 A 以大小等于谐振动角频率ω的角速度, 沿逆时针方向匀速转动, 这个矢量A 就称为旋转矢量.旋转矢量法是直观地研究谐振动的几何方法. 它不仅可以帮助人们形象地了解谐振动各物理量的含义及其相互关系, 而且便于对谐振动进谐激励力F0 co sωt 、与速度成反比的阻尼力- cv 因此,作受迫振动物体所受的合力为+ F0 co sωt -F = - k x由牛顿第二定律,得cv2md x= - k x + F0 co sωt - cv2d t2d x= - k x +F0sωt - c v∴d t2m m m取ω2 = k/ m ,2β= c/ m , f 0 = F0 / m ,并注意v =d x,0 d t代入上式得受迫振动的动力学方程为d2 x d x2+ 2βd t+ ω0 x = f 0 co sωt(1)d t2这是一个非齐次的常系数二阶微分方程.它的通解为A 0e -βt co s( 0 - β2 t + φ0 )ω2+ A c o s(ωt - δ)x =经过足够长的时间后, 其中第一项解减弱到可以忽略不计,只有第二项是振幅不变的振动.因此,受迫振动达到稳定状态时的运动学方程为[ 7]图 2作H G ⊥O G,在Rt △O G H 中,x = A c o s(ωt - δ)(2)F2 = ( B - D) 2 + C2式中A 是受迫振动稳态时的振幅;角频率等于简谐激励的角频率ω;δ是稳态响应与简谐激励的相差, 即受迫振动的初相. 式(2) 表示稳定状态的受迫振动是一个与简谐激励力同频率的简谐振动.f 2(ω2ω2 ) 2( βω) 2即=0 A - A + 2 A= A2 [ (ω2ω2 ) 2β2ω20 - + 4 ]βωA2βωC 2t a nδ===ω2 2 2 20 A -ω Aω0- ωB - D于是得受迫振动的振幅A 和初相δ分别为f 0用旋转矢量法求受迫振动的振幅和初相 A =(ω20- ω2 ) 2 + 4β2ω22βω由式( 2) 得δ= a r ct a nω2 2- ωd2 x= - ω A c o s(ωt - δ)2由此可知, 用旋转矢量法求受迫振动的振幅和初相,比用解微分方程的方法求解直观简单得多, 充分显示了用旋转矢量描述谐振动的优越性其实,任何谐振量都可以用旋转矢量来描述. 因此, 只要用得上旋转矢量法, 就要尽量应用它.d t2= ω2 A c o s[π+ (ωt - δ) ]2βd x = - 2βωA si n(ωt - δ)( 3)d tπ+ (ωt - δ)= 2βωA co s( 4)2参考文献ω20 x =ω0 A c o s(ωt - δ)2 (5)令B =ω2 A 、C = 2βωA 、D = ω2 A 、F = f 0 , 则式(3) 、0 [ 1 ] 赵景员, 王淑贤. 力学[ M ] . 北京: 人民教育出版社, 1979 .470～473赵凯华, 罗蔚茵. 力学[ M ] . 北京: 高等教育出版社, 1995 .273～275张三慧. 波动与光学[ M ]第2 版. 北京: 清华大学出版社,2000 . 24～25马文蔚,解希顺等. 物理学( 下册)[ M ] 第4 版. 北京:高等教育出版社,1999 . 30～31卢德馨. 大学物理学[ M ] . 北京: 高等教育出版社, 1998 .142～143刘克哲. 物理学(上卷) [ M ] 第2 版. 北京: 高等教育出版社,1999 . 155～156周圣源,黄伟民. 高工专物理学[ M ] . 北京: 高等教育出版社,1996 . 61 ,75( 4) 、( 5) 与式( 1) 的右边变为d2 x[ 2 ]= D co s[π+ (ωt - δ) ](6)d t2[ 3 ]π+ (ωt - δ)2βd x = C co s(7)2d t[ 4 ]ω20 x = B c o s(ωt - δ)( 8)(9)f 0 co sωt = F co sωt[ 5 ]将式(6) 、(7) 、(8) 、(9) 代入式(1) ,并用旋转矢量B 、C、D 、F 表示各谐振量, 则有F = B + C + D并且C ⊥B , D ⊥C.旋转矢量图如图2 所示.[ 6 ][ 7 ]。

旋转矢量法求初相位
旋转矢量法是指用矢量图来计算初始向量和另一个向量或一组向量之间的夹角。

它是利用空间的旋转矩阵进行计算的，并且可以同时求出多个向量之间的夹角。

该方法是一种非常有用的工具，在机械设计、飞行力学、定向技术等领域都有广泛应用。

旋转矢量法可以用来求出各种形式的初相位。

例如，可以用它来确定，一个物体沿某个方向移动多少距离后的初始方向。

这对定向技术是非常重要的，例如飞行控制系统、导航系统以及折叠飞行器等。

另外，它还被用来计算初相位去进行控制，例如运动伺服控制和机械自动化控制。

通常，旋转矢量法会先计算相对姿态，再换算成绝对姿态。

根据给定的空间四元数，可以用旋转矢量法得到空间三元数，这些三元数描述物体在空间中的运动状态，是计算初相位所必不可少的关键信息。

旋转矢量法带来了很多便利。

比如，它可以用来快速计算向量夆角，从而精确表示物体在空间中运动的姿态。

该方法可以帮助机械设计师清楚地表述物体的空间状况，极大地提高了工作效率，避免了人工误差。

旋转矢量法最重要的一点在于能够计算物体运动初始相位。

它可以方便的计算出各种运动的相位角，可以帮助研究者和技术
人员更加准确地表述物体在空间中的运动情况，有助于准确控制物体的运动。

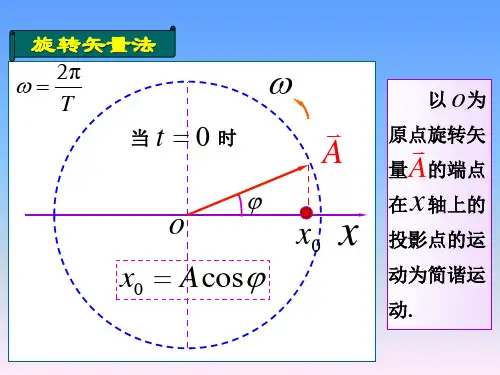
§ 8.3 旋转矢量法一、旋转矢量1 矢量的模等于简谐振动的振幅A长度 = A ；2 矢量绕O 点作逆时针方向匀速转动，其角速度的大小等于简谐振动的角频率以ω为角速度绕o 点逆时针旋转；3 在t = 0时，矢量A 和x 轴的夹角为ϕ ，在任意时刻t ，它与x 轴的夹角为ωt +ϕ ，矢量A 的矢端M 在x 轴上的投影点P 的坐标为 矢量端点在x 轴上的投影做简谐振动例 已知简谐振动，A =4 cm ，ν = 0.5 Hz ，t =1s 时x =-2cm 且向x 正向运动。

写出此简谐振动的表达式。

解：由题意，T = 2 s由图， ϕ = π/3，当旋转矢量A 旋转一周，投影点P 作一次完全的振动 ，旋转矢量A 的端点在x轴上的投影点P 的运动为简谐振动例8-4 一物体沿x 轴作简谐振动，振幅为0.24m ，周期为2s 。

当t = 0时，x 0= 0.12m ，且向x 轴正方向运动。

试求（1）振动方程（2）从且向x 轴负方向运动这一状态，回到平衡位置所需的时间。

已知：0.24m =A s 2=T 0.12m 0=x 00>v ∴x = 4cos(πt + ) cmπ 3t = 1s x()ϕω+=t A x cos求：解：（1）简谐振动的角频率t = 0时旋转矢量的位置如图所示振动方程为（2）令φ < 0这一状态对应的时刻为 t 1；回到平衡位置的时刻为 t 2。

t 1和t 2时刻的旋转矢量位置，如图所示例8-5 两个同方向(沿x 轴方向)、同频率的简谐振动，其频率都是2s-1。

当第一个振子从平衡位置向正方向运动0.05s 后，第二个振子正处于正方向的端点。

求这两个简谐振动的相位差。

已知：求：当第一个振子从平衡位置向正方向运动时，其旋转矢量A 1的位置如图所示经过0.05s 后，旋转矢量A 1转过一角度？）（ =t x （1） ？=∆t （2） 2π2πrad πrad 2ω T ===π3ϕ=-π0.24cos(π )m 3x t =- ()21ππ5π326t t ω-=+=215π6Δs 0.833s πt t t =-==-1212s ==νν10100,0x υ=>0.05s =∆t A x =2？=∆ϕ解： 简谐振动的角频率4π0.050.2πω t =⨯=此时，第二个振子刚好处在正方向端点，其旋转矢量A 2由图可见，两振子的相位差为第二个振子比第一个振子的相位超前二、相位差1 相位差和初相差相位差(phase difference)---相位之差。

旋转矢量法求初相位概述及解释说明1. 引言1.1 概述旋转矢量法是一种用于求解信号初始相位的数学方法，广泛应用于信号处理领域。

在许多实际问题中，准确确定信号的初相位对于数据分析和系统性能评估至关重要。

通过应用旋转矢量法，我们可以有效地估计信号的初相位，并将其应用于各种领域，如通信、雷达、图像处理等。

1.2 文章结构本文将按照以下结构进行介绍和解释：- 引言部分将对旋转矢量法求初相位的背景和意义进行概述。

- 旋转矢量法求初相位的理论基础将在第2节中详细阐述。

- 第3节将解释和说明旋转矢量的定义、性质以及该方法在信号处理中的作用。

- 第4节将介绍相关实验验证和结果分析。

- 最后一节为总结与展望，对本文内容进行概括，并探讨旋转矢量法求初相位在未来的应用前景。

1.3 目的本文的目的是全面介绍旋转矢量法求初相位这一方法，并从理论到实践层面进行详细阐述。

通过对方法的解释和说明，我们将揭示旋转矢量法在信号处理中的作用以及确定初相位的优势和局限性。

此外，通过实验验证和结果分析，我们将进一步验证该方法的有效性并提供相关数据支持。

最终，本文旨在为读者提供一个清晰全面的概述，并展望旋转矢量法求初相位在未来应用中可能发挥的重要作用。

2. 旋转矢量法求初相位2.1 理论基础旋转矢量法是一种用于求解信号的初相位的方法，基于信号在复平面上的表示和分析。

该方法利用了旋转矢量在复平面上的特性，通过对信号进行复数域运算和变换，得到信号的频率和初相位信息。

在时域中表示的信号可以看作是复平面上绕原点进行旋转的矢量。

根据欧拉公式，可以将一个复数表示为振幅与相位之间关系的指数形式：A*e^(jφ)，其中A为振幅，φ为相位角。

2.2 方法步骤旋转矢量法求解信号的初相位主要包括以下几个步骤：步骤1：获取待处理的信号数据，并进行预处理。

这一步通常包括去除噪声、滤波和采样等操作，以确保信号质量。

步骤2：对信号进行傅里叶变换或小波变换等频域变换，得到信号在频域上的表示。

大学物理学教学中初相位的求解——旋转矢量法
初相位的求解作为理论物理学中一个重要的内容经常被大学物理学教学中提及，相比较传统的三角函数法，旋转矢量法作为一种新的数学计算方式正逐步在各个大学物理教学中得到应用，本文将以此方式进行初相位的求解及应用。

旋转矢量法是一种计算变换位置、旋转之间关系的重要方法，可以把旋转视为矢量，这种矢量可以是旋转轴向量乘以旋转角度的形式。

在计算初相位时，可以利用旋转矢量的相加、相减，从而得出相应的位置、角度变换及旋转信息，从而解决初相位求解问题。

旋转矢量法具体应用于初相位求解时如下：
（1）以坐标系0-A，以A点为原点，以X轴为横轴，以Y轴为纵轴。

（3）从A点到B点的位移量为Rb，定义α角为旋转量，此旋转的旋转轴向量为：
U=(X`Y`Z`)。

（5）根据位移量Ra和α角，计算出旋转矢量：〖R_b〗^α=(X^`Y^`Z^`)。

（6）由计算出的旋转矢量〖R_b〗^α和位移量Ra，求出从A点到B点的旋转量Φ：Φ=〖R_a〗^α+Ra，Φ即为A点到B点的初相位。

（9）根据计算出的β角得出从A点到B点的旋转量γ：γ=β- α。

以上就是应用旋转矢量法求出初相位的步骤，3D旋转的运算角度可以根据同理求出。

传统的三角函数法只能表示2D的运算，而旋转矢量法则不仅可以求出2D的运算，还可以求出3D的运算，可以用来解决复杂的初相位求解问题。

总之，旋转矢量法作为一种基于几何的运算方式，其优点可以体现在于它融合几何和代数在一起，能够有效解决复杂多轴的位移、角度变换及旋转运算的问题，可以有效求解初相位问题。

从而为进一步的理论物理数学研究打下基础。

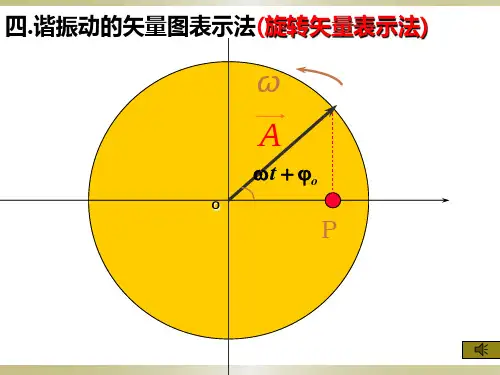
2.旋转矢量图法及其应用同学们好！旋转矢量法可以形象地表示简谐振动位移和时间关系，便于确定初相位，研究振动的合成。

下面我们一起学习旋转矢量法。

简谐振动的平衡位置为坐标原点O 点，水平向右为轴正方向，自原点O 点做一个矢量，矢量长度等于振幅A ，叫振幅矢量。

初始时刻，矢量A 与x 轴夹角等于振动的初相位ψ。

矢量A 从这位置以ω的角速度沿逆时针方向匀速转动，在任一时刻t ， 矢量A 与轴所成角度为ωt+ψ。

矢量A 在轴上的投影点与简谐振子的小球同步运动，位移相等，它在x 轴上的投影与时间用关系可用简谐振动方程表示。

矢量A 旋转一周，同时矢量的矢端在轴上的投影点完成一次简谐振动，投影点的运动可以形象地表示简谐振动，这种方法叫做旋转矢量法。

使用旋转矢量法还可以形象地了解简谐振动的振幅、角频率、初相位的物理意义。

显然，矢量A 做圆周运动的周期对应简谐振动的周期T ；矢量A 的圆周运动角速度对应简谐振动的角频率ω；初始时刻，旋转矢量的角度对应简谐振动的初相位ψ。

另外，使用旋转矢量法可以方便的确定物体的振动状态或初相位。

1. 由相位确定振动状态(1)简谐振动的相位是π/3，求振动状态I .旋转矢量图中，矢量A 的相位等于π/3，矢量A 的投影是物体的位移，等于A /2, 下一时刻矢量A 逆时针转动，所以简谐振动的小球向x 轴负方向运动。

(2)如果简谐振动的相位等于3π/2，求振动状态。

在旋转矢量图中，矢量A 的相位等于3π/2，矢量的投影点在x 轴的投影恰好在原点O , 所以物体的位移等于0， 矢量A 做逆时针转动，所以简谐振动的小球向x 轴正方向运动。

x x x2.由振动状态求初相位初始时刻，简谐振动的物体位移是A/2, 物体向x轴正方向运动，也就是速度大于0，初相位是多少？图中，矢量A在x轴的投影是A/2，表明矢量在第一或第四象限，且投影点向x轴正方向运动，从图示来看矢量A只能在第四象限。

因此初相位等于5π/3或-π/3。

旋转矢量法
矢量分析是研究数量物理学中最重要的方法之一，也是数学上最重要的分析工具之一。

矢量是两个平行线段（或者轴），用两个点表示，一个点是矢量的“起点”，另一个点是“终点”。

矢量的长度是从矢量的起点到终点的距离。

此外，矢量具有向量的属性，如方向和向量的场性质。

矢量的分析应用于几何、力学和电磁学等领域。

旋转矢量法（RVM）
旋转矢量法是一种应用于矢量分析的经典方法，它可以用于计算矢量的图形表示，也可以用于计算基本的向量图形。

一般来说，旋转矢量法是一种可以将一个向量从一个坐标系统转换到另一个坐标系统的方法。

原理介绍
旋转矢量法的基本原理是使用两个向量的叉积来旋转一个向量到另一个坐标系统，这两个向量分别称为被旋转矢量和旋转矢量。

如果从一个坐标系(A)旋转到另一个坐标系(B)，则使用被旋转矢量与旋转矢量的叉积，即可计算出旋转矢量在坐标系B中的表达式。

旋转矢量法还可以用来求解向量平面间的夹角和两个向量分量的夹角。

应用
旋转矢量法可用于计算图形学中的位置和方向，也可以应用于机器人、空间分析和三维图形模拟等技术。

此外，旋转矢量法还可以用于解决由向量和仿射变换组成的更复杂的数学问题。

总结
本文简要介绍了旋转矢量法，这是一种矢量分析的经典方法，可以用于计算矢量的图形表示和基本的向量图形，也可以用于解决由向量和仿射变换组成的更复杂的数学问题。

矢量分析方面的必要知识是可以理解旋转矢量法的基础，它需要计算坐标系之间的变换，以及向量的方向和向量的场性质。

在机器人，空间分析和三维图形模拟等技术中，旋转矢量法可以用于计算位置和方向。

探讨如何利用旋转矢量求解相位角求解谐振子的振动方程,关键是求解时刻振子的初相位。

求解波动方程,关键是求解处(坐标原点)的振子在时刻的初相位。

如果已知某个位置处的振子在时刻的振动位移和振动方向。

利用旋转矢量能很容易地定出该振子在时刻的相位。

1 旋转矢量介绍一个矢量处在平面直角坐标系内(如图1),与轴的夹角为,模长为,利用矢量解析法,可以得到该矢量在轴和轴上的投影值为:若矢量以角速度沿逆时针方向绕原点从角坐标处开始转动,在时刻,利用矢量解析法,可以得到该矢量在轴和轴上的投影值为(如图2):此时矢量的端点在轴上的投影点以原点为中心,在轴上来回作简谐振动。

其时刻的振动位移(振动方程)为矢量在轴上的投影值。

2 谐振子与旋转矢量把上述投影点当作谐振子,即以谐振子的振动中心为坐标原点,以振动所在的方向为轴,以振幅为半径作圆,抓住两点:(1)时刻谐振子(投影点)的位移是旋转矢量的投影值;(2)谐振子(投影点)的振动方向与旋转矢量逆时针转动方向对应。

可以画出谐振子与旋转矢量对应关系的旋转矢量图,如图3所示,设谐振子在时刻的位移为,谐振子(投影点)向轴负方向运动,过点作轴垂线,则垂线与圆有两个交点,连接原点到交点有两个矢量,这两个矢量在轴上的投影都是;点是旋转矢量端点的投影点,点向轴负方向运动,旋转矢量沿逆时针转动,因此与谐振子对应的是图中实线表示的矢量。

最后利用直角三角形各边关系可以求出时刻谐振子的振动相位,如果,即得到谐振子的初相位。

3 振动方向的判定3.1 振动曲线上时刻振子的振动方向振动曲线反映的是任意某个时刻该振子位置偏离平衡位置的位移情况。

可以用“顺描法”来判定时刻振子的振动方向,即顺着时间轴的正方向,根据时刻振子位移相对于时刻振子位移的变化情况来判定时刻振子的振动方向,如图4中时刻振子向轴负方向运动。

3.2 时刻波动曲线上位置处振子的振动方向波动曲线反映的是某个时刻处于不同位置处的各个振子振动位置偏离平衡位置的位移情况。