旋转矢量表示法B版
- 格式:pptx
- 大小:504.43 KB
- 文档页数:12



旋转矢量表示法高中物理的运动学、动力学大都以矢量表示,为了简单起见,通常采用“合矢”表示。
将有关运动矢量的矢量和分解成两个平行四边形,并指明两个平行四边形的夹角。
地球绕太阳的公转、卫星绕地球的公转、行星绕太阳的公转等都可用旋转矢量表示,但需要说明的是:所谓“公转”只不过是相对于观测者来说的,从一个观测者看来,地球上的每一点都在自西向东转动;而相对于地球的观测者来说,则是自东向西转动。
所以,由于地球上各点的位置在一年之中都不变,故“公转”也叫“平移”,它与“自转”同属角速度概念,并称为角动量的两个基本分量。
如果把太阳看作质点,则太阳绕地球公转的轨道平面就是以地球为焦点的双曲面。
根据动能定理,若把这一双曲面上的某一点P看作质点,则可得到太阳绕地球公转的轨道平面的另一种表达式——椭圆,其离心率为,为行星的半径,故称太阳为椭圆轨道的半长轴,称太阳轨道的长轴为太阳轨道的周期。
还可以证明:太阳的质量为,半径为,周期为地球的轨道平面与椭圆轨道的切线在赤道处的夹角称为地球的公转角速度。
通常以地球轨道的半长轴作为地球的周期,也就是说,地球绕太阳公转一周的时间称为年。
一般在电工学中经常遇到的情况是利用欧姆定律、焦耳定律、楞次定律或其他类似的定律。
电阻两端的电压u与通过导体横截面的电流i成正比,即,式中,是导体的电阻率,是材料的电阻率。
U是导体的内电压,是电源电动势,它决定于电流的参考方向和导体的电阻率,它是表示电源特征的一个物理量。
欧姆定律又称电功定律,是表示电流做功快慢的物理量。
焦耳定律是表示电流通过导体所消耗的热量多少的物理量。
下面介绍两种常用的方法,前者是由V=ir求欧姆定律,后者是由热功当量求焦耳定律。
前者可以直接由V=ir求出,然后再利用欧姆定律得到I,而后者必须先求出热功当量,然后根据热量、功、温度的关系(即热量=功×温度)求出。
另外,若需要知道闭合电路的欧姆定律或焦耳定律的微分形式,只要将公式略作变换,即可分别求出它们的微分形式。



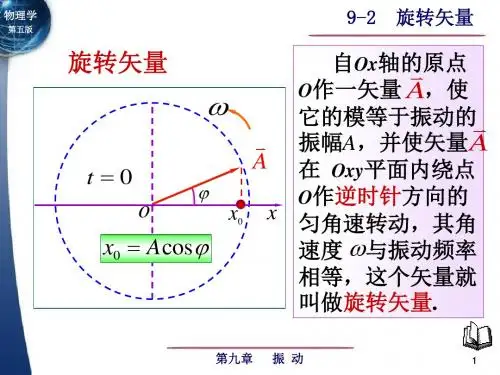
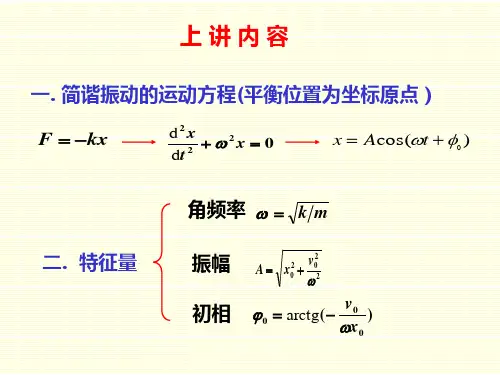
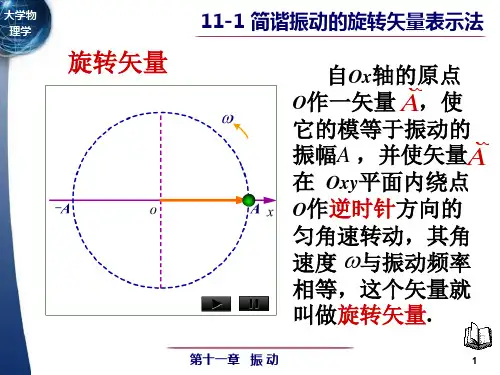
§ 8.3 旋转矢量法一、旋转矢量1 矢量的模等于简谐振动的振幅A长度 = A ;2 矢量绕O 点作逆时针方向匀速转动,其角速度的大小等于简谐振动的角频率 以ω为角速度绕o 点逆时针旋转;3 在t = 0时,矢量A 和x 轴的夹角为ϕ ,在任意时刻t ,它与x 轴的夹角为ωt +ϕ ,矢量A 的矢端M 在x 轴上的投影点P 的坐标为 矢量端点在x 轴上的投影做简谐振动例 已知简谐振动,A =4 cm ,ν = 0.5 Hz , t =1s 时x =-2cm 且向x 正向运动。
写出此简谐振动的表达式。
解:由题意,T = 2 s 由图, ϕ = π/3,当旋转矢量A 旋转一周,投影点P 作一次完全的振动 ,旋转矢量A 的端点在x 轴上的投影点P 的运动为简谐振动例8-5 两个同方向(沿x 轴方向)、同频率的简谐振动,其频率都是2s-1。
当第一个振子从平衡位置向正方向运动0.05s 后,第二个振子正处于正方向的端点。
求这两个简谐振动的相位差。
已知:-1212s ==νν10100,0x υ=>0.05s=∆t Ax =2∴x = 4cos(πt + ) cm π 3t = 1s x()ϕω+=t A x cos求:当第一个振子从平衡位置向正方向运动时,其旋转矢量A 1的位置如图所示 经过0.05s 后,旋转矢量A 1转过一角度此时,第二个振子刚好处在正方向端点,其旋转矢量A 2由图可见,两振子的相位差为第二个振子比第一个振子的相位超前2π4πradω ν==?=∆ϕ解: 简谐振动的角频率4π0.050.2πω t =⨯=π0.2π0.3π2ϕ∆=-=0.3πω1A。


旋转矢量法详细讲解
旋转矢量法是一种常用的三维空间中的旋转变换方法,它可以将一个三维向量绕着某个轴旋转一定的角度,从而得到一个新的向量。
这种方法在计算机图形学、机器人学、航空航天等领域都有广泛的应用。
旋转矢量法的基本思想是,将旋转变换分解为两个步骤:先将原向量绕着一个固定的轴旋转到一个特定的位置,再将其绕着另一个轴旋转到最终的位置。
这两个步骤可以用两个旋转矩阵来表示,它们的乘积就是最终的旋转矩阵。
具体来说,假设我们要将一个向量v绕着轴n旋转θ角度,那么首先需要将v投影到n所在的平面上,得到一个新的向量v'。
然后,将v'绕着n旋转θ/2角度,得到一个新的向量v''。
最后,将v''再绕着n的负方向旋转θ/2角度,就得到了最终的旋转向量。
旋转矢量法的优点在于,它可以避免旋转矩阵中的奇异性问题,从而提高计算的稳定性和精度。
此外,它还可以方便地进行复合旋转,即将多个旋转变换组合起来进行计算。
需要注意的是,旋转矢量法只适用于绕着固定轴进行旋转的情况,如果需要进行任意方向的旋转,就需要使用四元数或欧拉角等其他方法。
旋转矢量法是一种简单而有效的三维旋转变换方法,它在计算机图
形学、机器人学、航空航天等领域都有广泛的应用。
掌握旋转矢量法的原理和应用,对于进行三维空间中的旋转变换具有重要的意义。